三种工况下裸体状态数值假人的热传递模拟

黄紫薇，李 俊

（1.湖北理工学院 艺术学院，湖北 黄石 435003；2.东华大学a.服装与艺术设计学院；b.现代服装设计与技术教育部重点实验室，上海 200051）

三种工况下裸体状态数值假人的热传递模拟

黄紫薇1，李 俊2a，2b

（1.湖北理工学院 艺术学院，湖北 黄石 435003；2.东华大学a.服装与艺术设计学院；b.现代服装设计与技术教育部重点实验室，上海 200051）

为了探索一种能够取代暖体假人现场实验的有效途径，建立数值气候室，利用计算流体动力学（CFD）的数值模拟方法，在送风温度为20℃、速度为0.05m／s工况下，对数值假人体表自然对流边界空气层的温度、速度场分布及热传递属性参数进行模拟，然后在送风温度为20℃、速度分别为0.15和0.50m／s工况下，对室内混合对流的温度场和速度场以及热传递属性参数进行模拟.研究表明模拟结果具备很高的可靠性.

暖体假人；数值假人；计算流体动力学（CFD）模拟；热传递

暖体假人是模拟人体与环境之间热湿交换的仪器设备.在服装热湿舒适性评价和职业防护服开发中，暖体假人能在设定的环境下模拟人体、服装与环境间的热交换过程，科学地评价服装整体热学性能，从而避免了人体实验中个体差异的影响，实验精度高，可重复性好，被公认为服装工效学研究必不可少的手段.

由于暖体假人的制造工艺复杂，且价格昂贵，假人的实验条件如人工气候室成本高，因此，迫切需要找到新的研究手段来降低成本，或者取代暖体假人.近年来，随着计算机技术的发展，计算流体动力学（computational fluid dynamics，CFD）有了更加广泛的应用，利用CFD对有人的通风室内热环境研究越来越深入［1］.目前，国内主要从气流组织和污染物浓度等方面对室内的大环境进行研究［2］，而鲜有学者利用CFD技术，从人体微环境出发，模拟并研究人体裸体体表热边界层的温度场与速度场分布规律.

文献［3］利用东华大学服装学院人工气候实验室及暖体假人进行现场实验，以人工气候实验室与暖体假人为原型建立数值气候室与数值假人，利用CFD技术对暖体假人现场实验进行再现与模拟，检验了模拟结果与现场实验的一致性.本文在位于优化数值气候室内的3种工况下，对裸体状态数值假人的体表边界空气层、室内的气流速度场与温度场进行了稳态数值模拟计算.

1 数值假人的三维形体

本文以东华大学自主研制的暖体假人（如图1所示）为原型建立数值假人，其形态分为11个独立的加热体段，即：1头颈部，2头颈关节，3胸背部，4腰关节，5腹臀部，6踝关节，7脚，8小腿，9膝关节，10大腿，11胯关节，12臂，13肩关节.该暖体假人固定于人工气候室内，气候室的长、宽、高分别为1.98，2.08，1.98m.

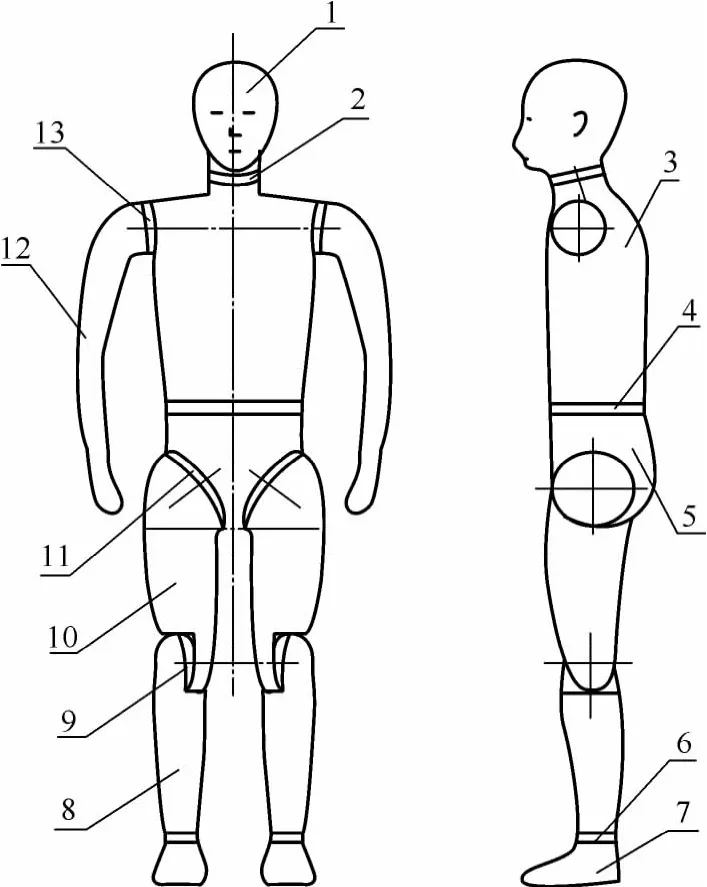
图1 暖体假人的构成Fig.1 The structure of thermal manikin

以实验室假人体段数、各体段的高度、表面积等相关数据为依据，建立模拟用数值假人，模型面积与暖体假人的实际表面积对比数据如表1所示.二者对应体段的表面积相对误差均可基本忽略.

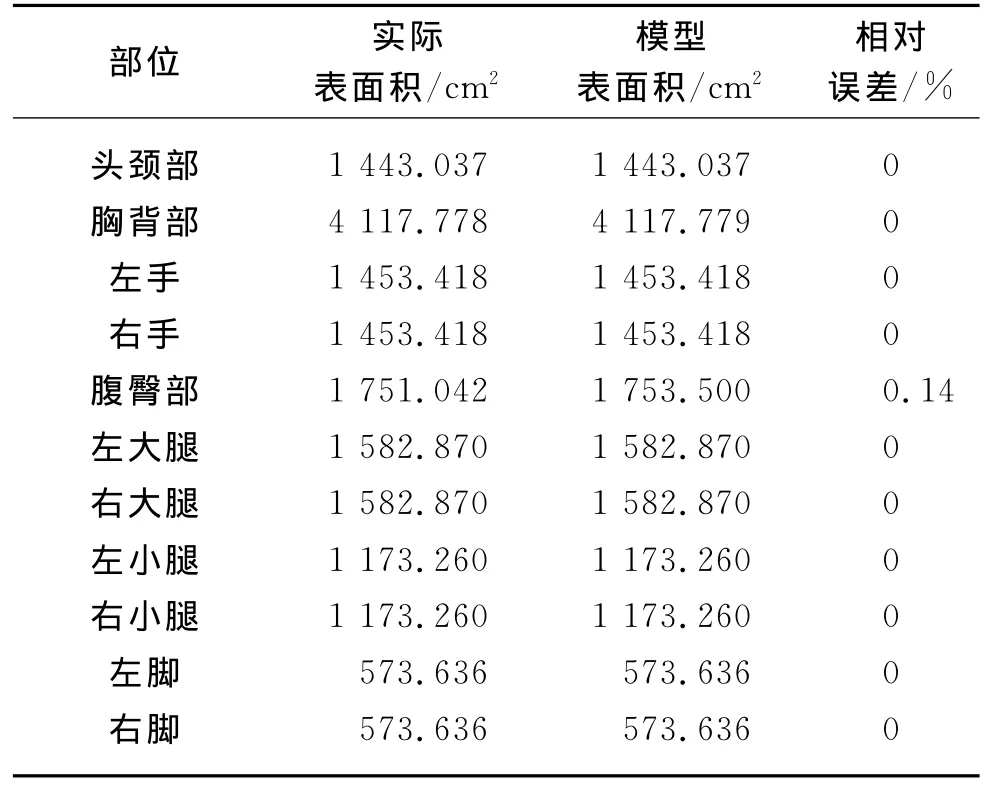
表1 暖体假人与数值假人各体段的表面积Table 1 The surface area of each segment of thermal manikin and numerical manikin

人体在无风的情况下（风速＜0.1m／s，可认为是无风环境［4］），散热使得人体周围空气受热发生自然对流.对于裸体站立者，体表附近的空气受到向上的浮升力作用，热空气沿体表向上运动，产生自然对流.这股受到人体散热形成的气流，在人的头顶向上仍然可以维持1～1.5m的高度，然后才消失在空气中［5］.因此，室内高度至少要比人体身高高出1～1.5m，才能得到在头顶充分扩散的热气流.本文建立与人工气候室相同长、宽，不同高度（2.5m）的优化数值气候室，左侧底部中间为送风口、右侧顶部中间为出风口，风口尺寸均为0.3m×0.3m，如图2所示.沿人体体表向上的自然对流比较微弱，自左下向右上方向的送风系统可以加强自然对流的效果，来充分显示浮升气流的运动情况.

图2 优化数值气候室及数值假人Fig.2 Optimized numerical climate chamber and numerical manikin

2 网格划分

针对人体复杂的三维形体，可采用非结构网格对计算域进行离散.对计算域的划分依次从线网格、面网格到体网格.

按照固定节点距离（interval size）的方法，对线网格进行分部位划分.对于曲率变化大的部位（例如人体的腋下）、线与线之间距离非常接近的部位（例如腹臀部与大腿相接处）需要划分较细密的节点，所以采用较小的节点距离.另外，节点之间的过渡也很重要.

对线网格划分采用3种方式：（1）定比且双向分布.该方式用于人体模型的臀部与大腿截面相接处的划分，节点集中于两者截面非常接近的部位.（2）定比且单向分布.该方式用于人体模型的腋下与胸背部相接部位，方向为从腋下指向腰部，以及腋下指向手臂.（3）等距离分布.该方式用于人体模型的其他部位、送风口和回风口以及房间的各边.

考虑到网格质量与计算耗时，面划分采用三角形单元，体划分采用四面体网格.优化数值气候室内空间较大，从较小的节点距离（人体体表）过渡到较大的节点距离（房间内部的空间），临近单元体积的快速变化会导致大的截断误差.为了使整个计算域内网格节点的圆滑过渡，计算域由一个内部的体（interior）分割为两个区域（如图3所示）.由图3可知，人体表面的网格进行了加密，优化数值气候室内体积1的网格较体积2内的网格单元更细密.最后得到72 295个节点，356 986个非结构化网格单元.

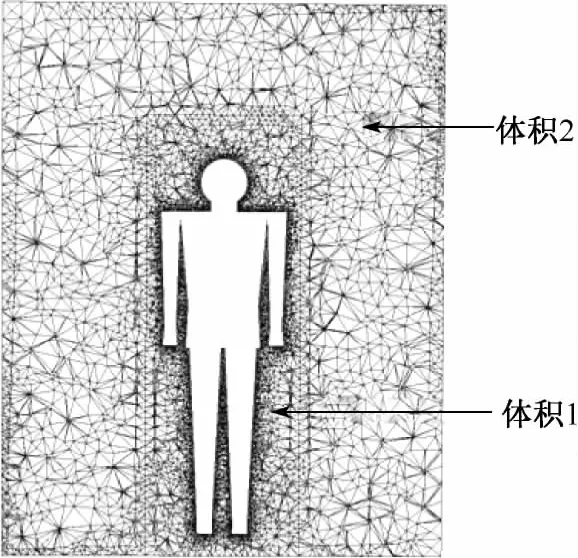
图3 优化数值气候室内网格分布截面图Fig.3 The grid distribution of optimized numerical climate chamber

3 模型选择及参数设定

选用RNGκ－ε模型［6－8］来模拟室内气流组织，考虑浮升力的影响，利用表面辐射模型（S2S）来计算人体与墙壁间的辐射换热.为了能够在现有条件下最大尺度地反映实际情况，对物理模型作以下假设：

（1）本文模拟的假人实验室内为低速流动的空气，可以认为实验室内的气流不可压缩，并考虑了质量力的作用，实验室内的流场、压力场均视为三维稳态.

（2）由于实验室内温差不是很高（送风温度为20℃，人体表面温度约为33℃），符合Boussinesq近似，按照稳态计算.

（3）由于本文的模拟过程中除了人体散热以外，不涉及大功率的电器设备，所以假设四面墙壁结构均绝热.

计算的边界条件如表2.求解的控制参数如表3所示.

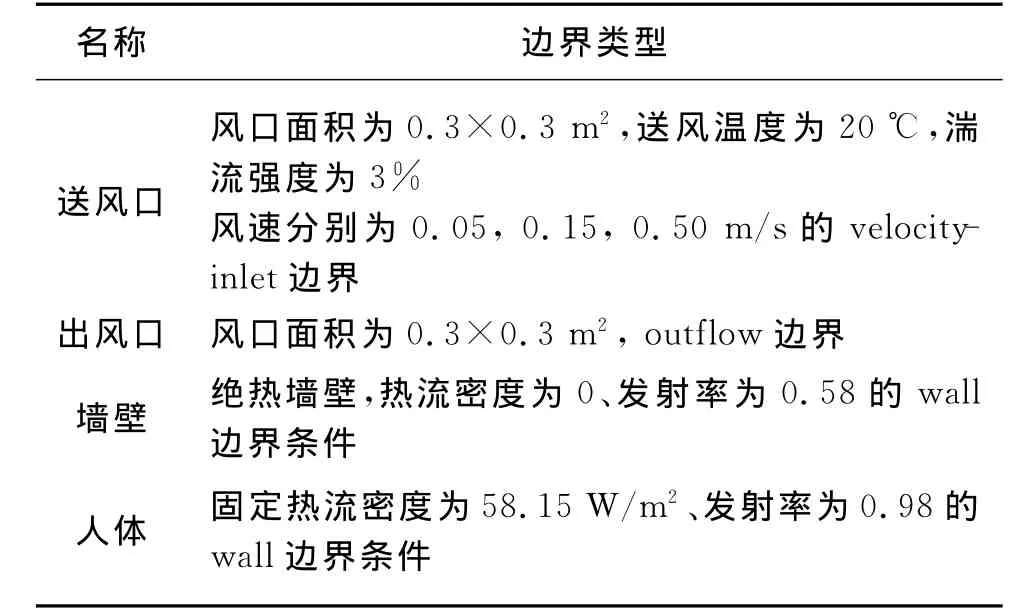
表2 边界条件及参数Table 2 Boundary conditions and parameters

表3 求解参数Table 3 Solution parameters

4 结果及分析

4.1 角系数

角系数（view factor）Fjk是离开表面k的辐射量被表面j所接收到的比例.某个表面接收到另一个表面的入射辐射量是这两个表面角系数Fjk的函数.表4是优化数值气候室内人体与房间各墙壁之间的角系数值.

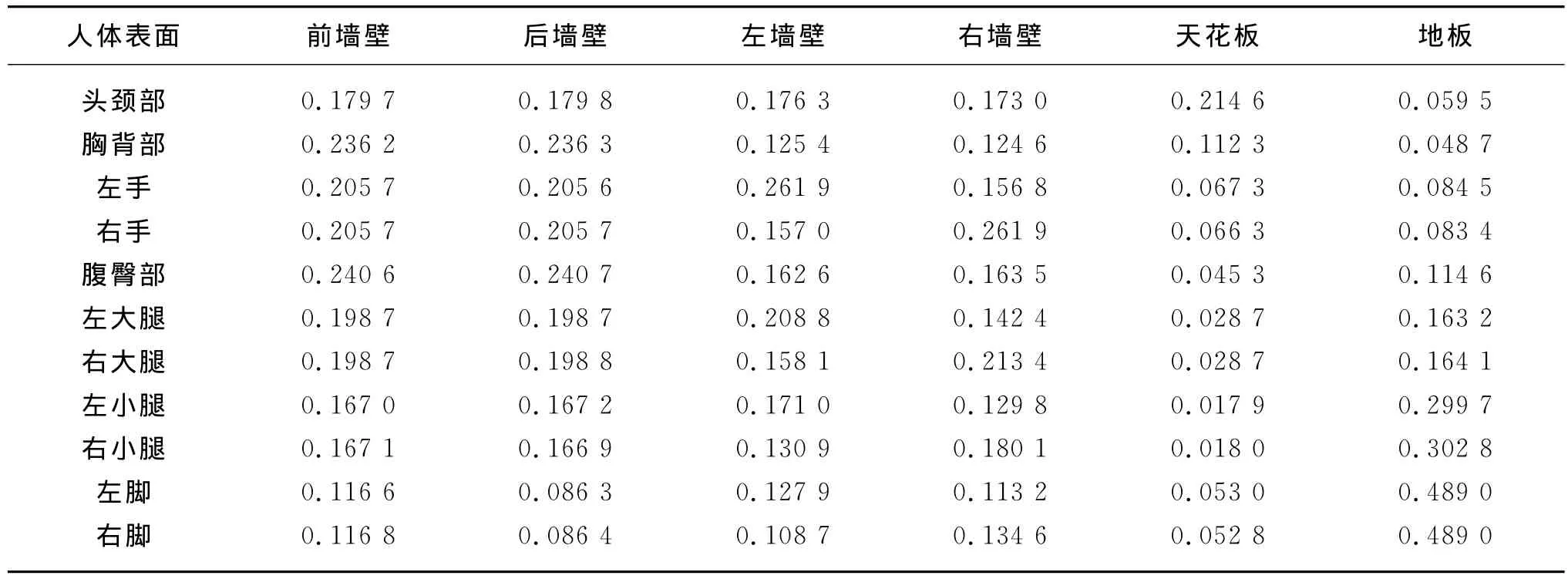
表4 优化数值气候室中人体表面与各墙壁间的角系数Table 4 View factors between body surface and walls in the optimized numerical climate chamber

由于优化数值气候室的前后墙对称、左右墙壁旋转对称，角系数也呈现一定的对称性.由表4可知，前、后墙壁接收到人体11个体段的辐射能量，其中接受腹臀部的辐射热最多，胸背部的辐射热略小.虽然腹臀部的表面积小于胸背部的表面积，由于胸背部的左右侧分别受到左右手的阻挡，从而减少了有效辐射面积.前后墙壁接受左右脚的辐射热最小，这是因为脚部的表面积最小，而且脚的位置低，与前、后墙壁竖直向上的距离越来越远.

左墙壁的底边中央处有送风口，右墙壁的顶边中央处有出风口.左、右墙壁分别接收到左、右手的辐射热最多；左、右大腿次之；左、右脚最少.左、右手的表面积小于左、右大腿的表面积，但是左手与左墙壁、右手与右墙壁之间的距离更近，因而接受更多的辐射热.另外，左手与左墙壁、右手与右墙壁之间的角系数呈现对应的规律，这与二者之间的位置关系相吻合.左右大、小腿处于房间高度方向的中部偏下处，而左墙的送风口减少了接受辐射的面积，所以左墙壁接受左大、小腿的辐射热稍小于右墙壁接受右大、小腿的辐射热.

天花板接受头颈部的辐射热最多，接受胸背部的辐射热较少，这两个部位散失的辐射热占据天花板接受的辐射量中的绝大部分.这是因为头颈部离天花板距离近，而胸背部虽然表面积大，但由于头颈部以及左右手的阻挡，天花板接受胸背部的辐射热较少.数值假人的其他部位对于天花板而言，主要因为受到自上而下的其他部位的阻挡以及二者之间的距离渐远的影响，除了脚踝部位同样受到小腿的阻挡以外，脚背部分仍可辐射热量给天花板，所以左右脚的角系数相对较大.

地板接受左右脚的辐射热最多，接受自小腿以上至胸背部的辐射热依次减少，最少的是头颈部和胸背部，胸背部的表面积远大于头颈部的表面积，而且胸背部离地板近，但是由于人体胸背部被相邻的腹臀部等身体部位阻挡，而头颈部为球体，除了被阻挡外，还有一部分面积直接与地板相对，所以头颈部对地板的辐射热稍大于胸背部对地板的辐射热.

4.2 在0.05m／s送风工况下的热传递模拟

当室内风速为0.05m／s时，模拟得到优化数值气候室内数值假人表面空气层的自然对流相关数据如表5所示.由表5可知，由于人体左右对称，模拟计算得到各体段产热量表现出对称性，这与实际吻合，其中人体的胸背部、腹臀部、大腿、头颈部和手占据人体主要的面积，因此相应产生大部分的热量.

表5 优化数值气候室内0.05m／s送风时相关数据Table 5 Relevant data at 0.05m／s in optimized numerical climate chamber

虽然人体的表面积左右对称，但是人体左右手、左右腿脚的辐射散热量以及温度存在差异，这与房间左右墙壁的风口位置以及送风情况有关.由人体从上至下来看：在总的辐射散热量中，胸背部散失的热量最多；其次是腹臀部和头颈部；自腹臀部向下至脚部，辐射量依次减小；脚部的辐射热散失最少.从人体左右的对称部位来看：右手、右大腿、右小腿部位的辐射散热量略大于左边对应部位的散热量，而左脚的辐射热略大于右脚.

在外界温度较低，机体处于安静状态时，辐射热占总散热量的60%左右［5］.本工况下，送风温度为20℃，风速为0.05m／s，人体处于静止站立状态，体表发生自然对流，数值假人辐射热占新陈代谢产热量的59.65%，二者非常接近.

优化数值气候室内各墙壁以及天花板和地板之间的平均温度以及辐射热如表6所示.室内墙壁属于绝热边界条件，其本身不产生热量，与假人体表以及其余墙壁之间发生辐射传热，与壁面附近的空气发生对流传热.由表6可以看出，各墙壁的平均温度与周围空气的温度接近.地板的温度最低，其左侧紧挨送风口，送风温度仅为20℃，所以温度较低，因此，地板从数值假人和其他墙壁获得的辐射热最多.天花板的温度最高，因为人体代谢产热，使得周围的空气受热向上运动至天花板附近，天花板受到热空气的作用导致温度上升，因此，天花板向数值假人和其他墙壁散失辐射热.前后、左右的墙壁温度较一致，均接近于26.79℃.

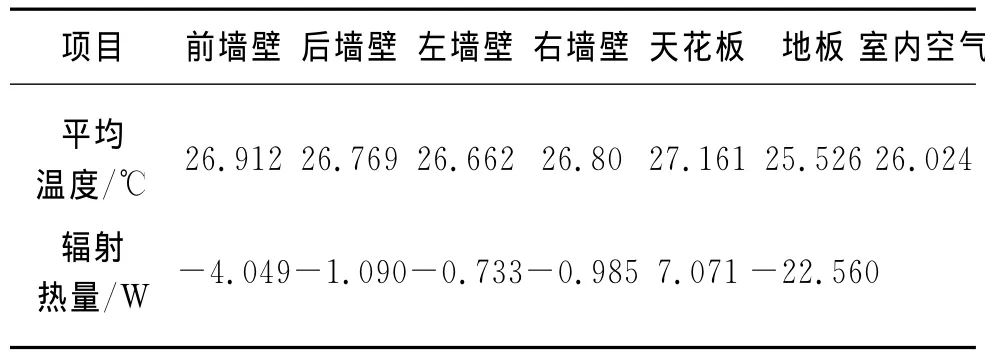
表6 优化数值气候室内各墙壁的温度（送风速度0.05m／s）Table 6 The temperature of each wall at 0.05m／s in the optimized numerical climate chamber

在优化数值气候室模型中取y＝0的截面，得到送风速度为0.05m／s的室内温度分布图，如图4所示.数值假人与室内空气发生自然对流，因此，室内温度在垂直方向上存在温度梯度.左侧底部是送风口，由于送风温度较低，左侧空气的温度分层较密.由于发热人体的阻隔，右侧空气的分层较疏，而且左右两侧越接近室内的上部，空气温度有趋于一致的趋势.人体自脚部产生自然对流热边界层，在人体的头部上方温度达到最高，从而使得室内的空气温差达到10℃.

图4 优化数值气候室内y＝0截面温度分布图［3］Fig.4 Distributions of air temperature in the plane of y＝0in the optimized numerical climate chamber

由于自然对流，人体表面除了产生温度边界层以外，还存在速度边界层，如图5和6所示.人体表面温度高于室内空气温度，自然对流的结果使人体表面形成一股热上升的气流.该气流自脚开始，速度较小，厚度也较小，但在上升过程中得到发展.虽然送风速度仅为0.05m／s，但是由于热气流的作用，在人体的头顶上，这股气流的速度可以达到0.244 m／s.

图5 优化数值气候室内y＝0截面气流速度矢量图Fig.5 Distributions of air velocity vector in the plane of y＝0in the optimized numerical climate chamber

图6 x＝0.08m截面处速度图［3］Fig.6 The velocity distributions in the plane of x＝0.08min the optimized numerical climate chamber

本文仅考虑数值假人的干性散热，包含了辐射散热和对流散热.根据Fluent的相关计算，得到处于优化数值气候室内数值假人与房间的各墙壁之间的辐射以及对流换热系数，如表7和8所示.

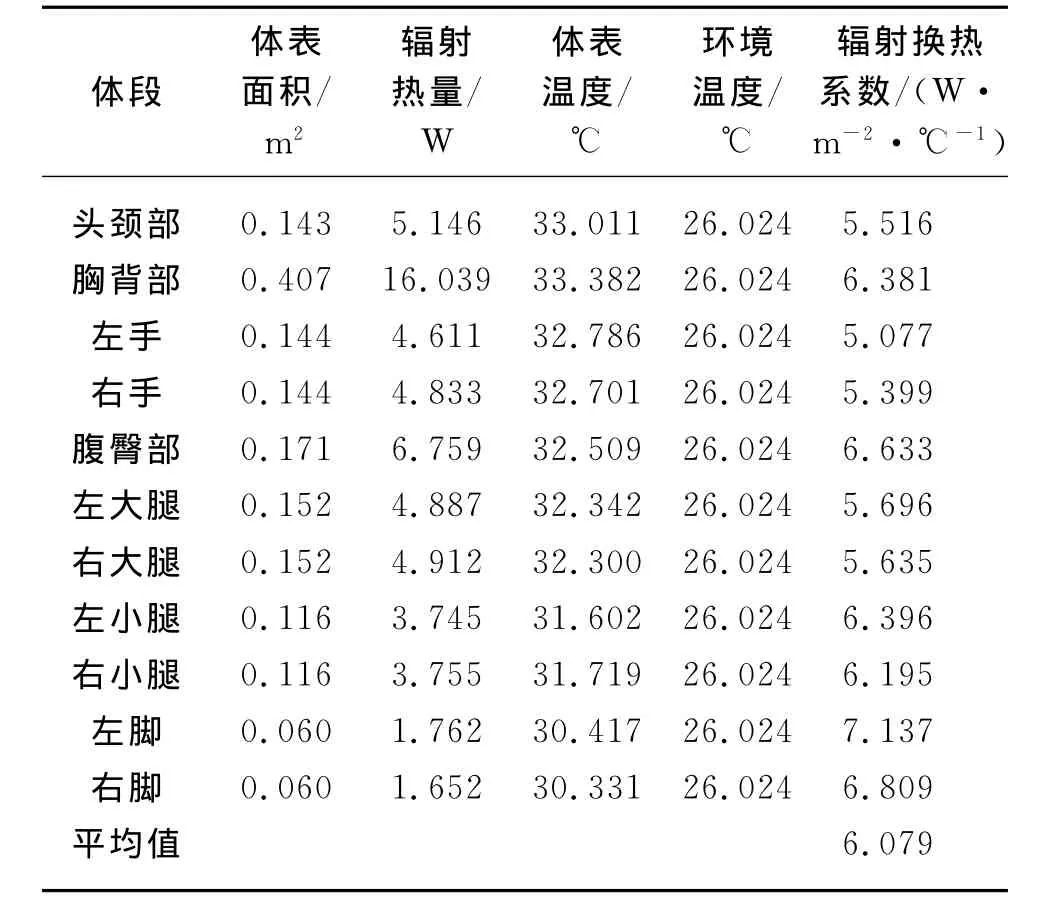
表7 优化数值气候室内数值假人局部的辐射换热系数Table 7 The local radiate heat transfer coefficient of numerical manikin in the optimized numerical climate chamber

常温下，单位辐射换热系数hr为5.7W／（m2·℃），或近似地表达为hr＝4.6（1＋0.01tmrt）［5］，其中tmrt为平均辐射温度（℃）.利用各体段的表面积与温度计算得到数值假人与气候室内各墙壁之间的平均辐射温度为32.500℃，代入近似表达式，得到优化数值气候室内的hr为6.095W／（m2·℃），通过模拟计算得到该系数为6.079W／（m2·℃），二者相对误差仅为0.26%.而对于对流换热系数hc，拉普（Rapp）建议的数值为hc＝4.0W／（m2·℃）（0.05m／s＜风速＜0.2m／s，1＜Δt＜15℃时，Δt为温差）［5］.经过模拟计算得到hc为4.393W／（m2·℃），二者存在差异.在优化数值气候室内，送风速度为0.05m／s，室内的最大风速达到0.256m／s，对流作用在一定程度上加剧，因此，优化数值气候室内的对流换热系数偏大.

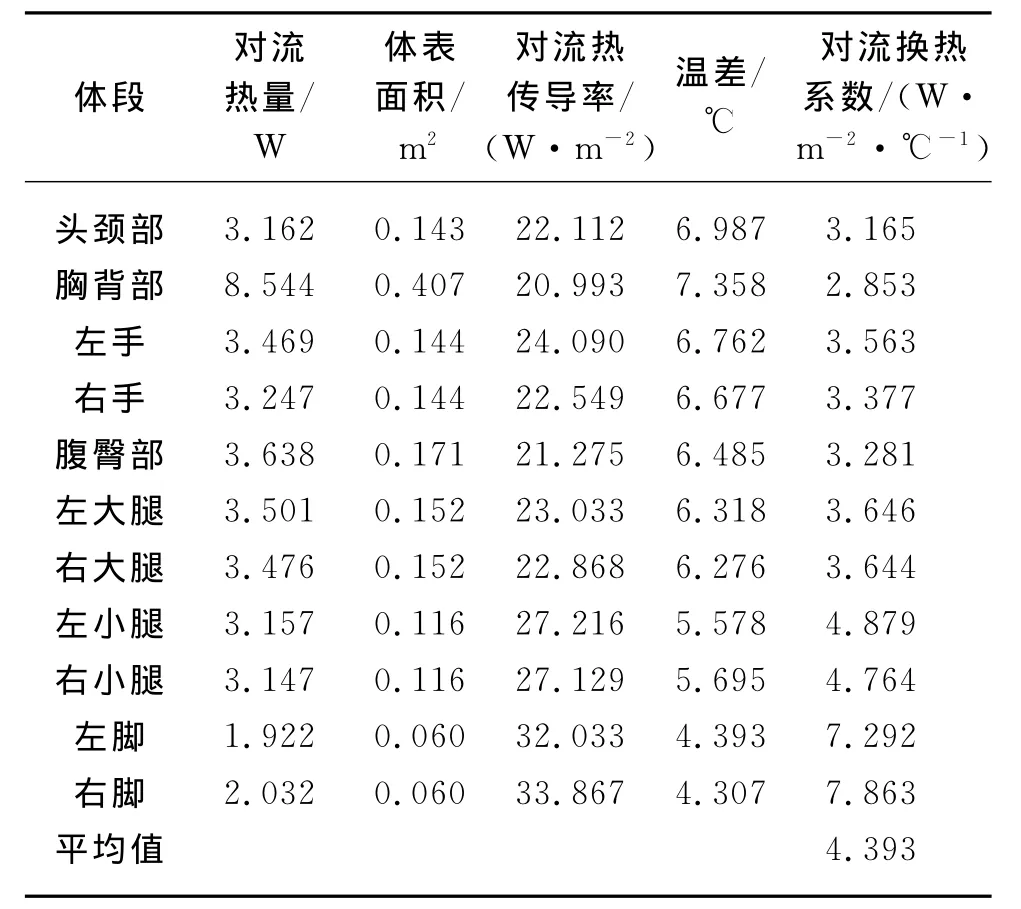
表8 优化数值气候室内数值假人局部的对流换热系数Table 8 The local convective heat transfer coefficient of numerical manikin in the optimized numerical climate chamber

4.3 在0.15和0.50m／s送风工况下的热传递模拟对比

风速的增加可以改变空气的流动状态，提高湍流强度.在风速为0.15和0.50m／s下，室内气流是自然对流与强迫对流的混合对流.在两种工况下数值假人各体段的辐射热量和温度如表9所示.由表9可知，在优化数值气候室内，人体不同部位的辐射热量和平均温度均随送风速度的增加而减小.人体的辐射热量与有效辐射面积、角系数、环境温度有关.

胸背部占据最大的表面积，其辐射热量最大；腹臀部的表面积其次，其辐射热量占人体总辐射热的第二大部分，有效辐射面积起主导作用.虽然大腿部面积大于头颈部，然而在低风速下（0.15m／s），两者与其他辐射面之间的位置关系起主导作用，头颈部直接与天花板进行辐射换热，而大腿部位上下分别受到腹臀部和小腿部位的阻碍作用，所以大腿部位相对于头颈部的辐射热有所减弱；但在较大风速情况下（0.50m／s），大腿部位的辐射热反而大于头颈部，此时，风速降低了室内的温度，从而使得辐射传热作用降低.脚部由于表面积较小，且处于送风口的位置，所以辐射热量最小.

1) 对比A、B、D 3个模型骨架曲线(图8)可以发现，模型B的极限承载力较模型A增长57.64%，模型D增长38.3%.可以发现增设抗震墙后结构的承载能力明显提高，同时也可以得出抗震墙布置在跨中时结构的极限承载力提高幅度最大.

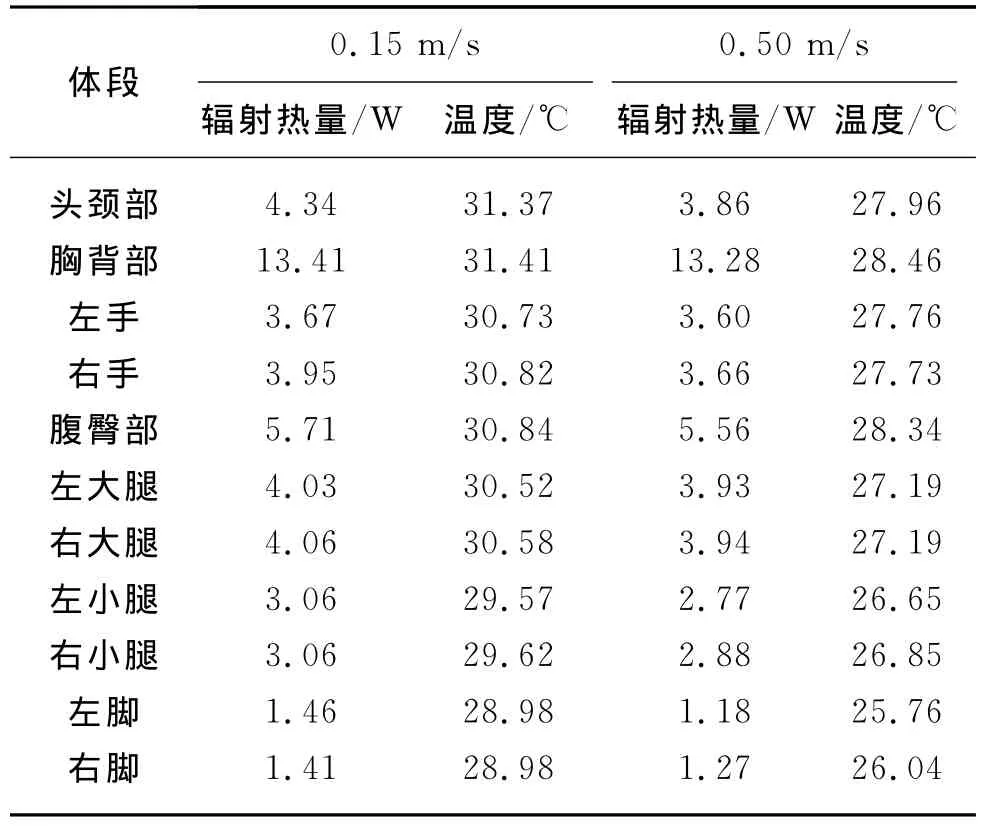
表9 两种工况下数值假人各体段的辐射热量与温度对比表Table 9 Comparison of radiate heat and temperature of each segment of numerical manikin under two conditions

在两种送风工况下，数值假人各体段的表面温度：头颈部、胸背部、腹臀部的温度均较高，自大腿向下至脚部，人体的温度逐渐降低，这与实际人体相吻合.

当送风速度为0.15m／s时，在优化数值气候室内y＝0截面处的温度及速度分布如图7所示.由图7可知，优化数值气候室内温差为6.4℃，由地板到天花板的温度梯度比较明显.由于人体代谢产热使得体表周围的空气受到向上扩散的浮升力，而室内送风也是下送上回，使得体表空气受到的浮升力作用加强，从而在室内产生自下而上的温度分层分布气流.

当送风速度为0.50m／s时，在优化气候室内y＝0截面处的温度及速度分布如图8所示.由图8可知，优化数值气候室内温度趋向于均匀分布，温差仅为4℃.从室内的温度分布来看，仍然可以看到人体代谢产热驱使下热空气浮升的效果.从室内风速分布可知，室内空气为充分发展的湍流，湍流有助于人体产热与周围冷空气的热交换.冷空气进入的风速较小时，人体代谢产热对空气的热影响作用占据主导；而随着风速的增加，冷空气的作用逐渐取代人体代谢产热的作用，此时，人体安静时的代谢产热不足以影响通风室内的空气温度.

图7 优化数值气候室内在0.15m／s风速下y＝0截面处的气流温度及速度分布图Fig.7 Distributions of air temperature and air velocity in the plane of y＝0at 0.15m／s in the optimized numerical climate chamber

图8 优化数值气候室内在0.50m／s风速下y＝0截面处的气流温度与速度图Fig.8 Distributions of air temperature and air velocity in the plane of y＝0at 0.50m／s in the optimized numerical climate chamber

5 结 语

本文利用CFD数值模拟方法计算了在0.05m／s送风工况下，数值假人体表自然对流边界层的温度场分布，在数值假人头部上方温度达到最大值30℃，从而使得优化数值气候室内温差为10℃，模拟计算得到该工况下辐射换热系数为6.079W／（m2·℃），对 流 换 热 系 数 为 4.393 W／（m2·℃），模拟计算与文献提供的参考值较为一致.在风速为0.15和0.50m／s工况下，室内气流是自然对流与强迫对流的混合对流.当送风速度为0.15m／s时，优化数值气候室内温差为6.4℃；当送风速度为0.50m／s时，优化数值气候室内温度趋向于均匀分布，温差仅为4℃.随着风速的增加，冷空气的作用逐渐取代人体代谢产热对空气的热影响，室内温度趋于一致.

CFD数值模拟为研究人体与环境热交换提供了一种方便有效的方法，它不仅能够在一定程度上取代暖体假人，而且可以克服气候室在尺寸和在送风方面的局限性.

参 考 文 献

［1］彭关中，缪小平，刘文杰，等.办公室空调房间热环境数值模拟研究［J］.建筑热能通风空调，2009，28（3）：54－57.

［2］刘玉峰，徐永清.房间气流组织对污染物空间分布的影响［J］.山东科技大学学报：自然科学版，2004，23（2）：104－107.

［3］WANG Y Y，HUANG Z W，LU Y H，et al.Heat transfer properties of the numerical human body simulated from the thermal manikin［J］.Journal of the Textile Institute，2013，104（2）：178－187.

［4］GB／T 18398—2001，服装热阻测试方法，暖体假人法［S］.

［5］姜怀，林兰天，孙熊.常用／特殊服装功能构成、评价与展望：上［M］.上海：东华大学出版社，2006：128－141.

［6］CHEN H C，PATEL V C.Near－wall turbulence models for complex flows including separation［J］.AIAA Journal，1988，26（6）：641－648.

［7］KOESTEL A，TUVE G.Performance and evaluation of room air distribution system ［J］.ASHRAE Transactions.1968，61：533.

［8］AL－MOGBEL A M.Analysis of human thermal comfort using a coupled model for predicting human body－environment heat and mass－exchanges［D］.Old Dominion University.2004.

Heat Transfer Simulation of Naked Numerical Manikin under Three Conditions

HUANGZi－wei1，LIJun2a，2b
（1.Art Institute，Hubei Polytechnic University，Huangshi Hubei 435003，China；a.Fashion and Art Design Institute；b.Key Laboratory of Clothing Design and Technology，Ministry of Education，2.Donghua University，Shanghai 200051，China）

In order to explore an effective way to replace the manikin field experiment，a numerical climate chamber was set up.With the method of computational fluid dynamics（CFD）simulation，the temperature and velocity fields together with heat transfer parameters of boundary air layer around numerical manikin were simulated under the condition of a supply air temperature of 20℃ and velocity of 0.05 m／s.And then，under the condition of a supply air temperature of 20℃and velocity of 0.15 m／s together with 0.50 m／s，the temperature and velocity fields as well as heat transfer parameters of mixed convection indoor were simulated respectively.The research shows the simulation results have a high reliability.

thermal manikin；numerical manikin；computational fluid dynamics （CFD）simulation；heat transfer

TS 941.17

A

1671－0444（2014）04－0461－08

2013－12－24

湖北理工学院校级青年基金资助项目（11yjr46Q）

黄紫薇（1983—），女，湖北孝感人，讲师，硕士，研究方向为服装舒适性与功能.E－mail：huangziwei822＠126.com