中空长航时无人机高升力层流翼型综合设计

李权, 曹燚, 冯海勇, 雷武涛

(1.西安飞机设计研究所 总体气动设计研究所, 陕西 西安 710089;2.西安飞机设计研究所 院长办公室, 陕西 西安 710089)

0 引言

中空长航时无人机是当前无人机家族的重要组成部分,如美国的“捕食者”系列、以色列的“苍鹭”等。该类无人机具有较高的升阻比,以维持较长的巡航或巡逻飞行时间,顺利执行侦察、跟踪或中继引导等任务。因此,该类无人机一般采用大展弦比、小后掠或直机翼;使用厚翼型,保证机翼提供充足的空间装载更多燃油。文献[1]表明,该类典型无人机的起飞重量约1 000 kg,起飞翼载约80 kg/m2,飞行高度6 000～7 000 m,飞行速度约170 km/h。按照上述参数测算,该类无人机的巡航/巡逻升力系数接近1.0,远高于常规飞机;飞行雷诺数约1.5×106,远低于常规客机。由于飞行雷诺数低,该类无人机可考虑采用层流翼型改善飞机的升阻特性,提高飞机巡航性能。根据无人机的使用特点,该层流翼型需在高升力状态下稳定工作,具有抵抗飞行性能因层流提前转捩大幅下降的能力。

1 设计要求

参考“捕食者”无人机,层流翼型设计要求为:

设计工况:Ma=0.15,Re=1.5×106；

目标:CL=1.1, 升阻比K最大；

约束条件:(1)俯仰力矩系数Cm大于-0.1;(2)巡航点附近,湍流状态的升力系数下降量不超过自由转捩状态相同迎角的升力系数的10%;(3)湍流工况的最大升力系数CLmax大于1.4;(4)翼型最大相对厚度大于16%。

该类无人机需在高升力状态下长时间工作,而常规翼型在高升力状态具有较大的低头力矩,全机配平阻力偏大,降低了飞机升阻性能。因此,引入约束条件(1),要求翼型在设计工况具有适中的俯仰力矩。实际飞行中,层流翼型不可避免地会遇到因表面污染等原因引起层流提前转捩,导致飞机性能发生改变的情况。为保障飞行安全,层流翼型设计时需考虑不会因提前转捩而引起飞行安全的要求,因此设定了约束条件(2)。

2 设计方法

对于复杂工程问题,各种要求之间往往是相互矛盾的,需采用一定的策略进行多目标多约束综合设计。根据本文问题特点,采用考虑层流转捩的气动力求解技术和多目标优化遗传算法,构建了翼型综合优化设计平台。

2.1 翼型参数化

翼型参数化采用Kulfan等[2]提出的基于类函数/型函数的参数化方法(class function/shape function transformation, CST),其具体表达式为:

翼型上、下表面分别为:

yu=C(x)Su(x)+xyTEu

yl=C(x)Sl(x)+xyTEl

式中,yTEu,yTEl分别为上、下表面后缘的y坐标。

类函数定义:

C(x)=xN1(1-x)N2

型函数定义:

其中:

式中,N1和N2分别取0.5和1.0;Aui和Ali为待定系数;Si(x)为Bernstein多项式。

Kulfan经过推导指出,Au0和Al0与翼型的前缘半径RLE有直接联系:

由上述分析可知,只要确定系数Aui和Ali,整个翼型即可以确定;上述参数可采用最小二乘法求解得到。

2.2 气动力求解

(1)基于XFOIL的快速气动力求解

XFOIL是由Mark Drela开发的一款低速和亚声速翼型的分析和设计软件,采用高阶面元法,通过有粘或无粘迭代计算翼型气动力,具备较高的分析和设计效率。转捩预测方面,XFOIL采用基于线性稳定性理论的eN方法进行转捩判定。eN方法是一种半经验方法,基本思想是假设层流边界层产生的最初小扰动以不变的频率向下游发展,当扰动值放大到原来的eN倍时认为流动发生转捩(见图1)。N因子需要通过试验或数值模拟确定,风洞环境下一般取9,飞行试验取10～18[3]。文献[4]研究表明，XFOIL软件可准确预测低速翼型的层流转捩,适用于低速层流翼型设计。

图1 层流边界层转捩示意图Fig.1 Expression of laminar boundary transition

(2)基于N-S方程的精细气动力求解

XFOIL具有较高的求解效率,适用于优化设计迭代,但最终结果需采用基于N-S方程的高精度流动求解器进行校核。本文采用ANSYS-CFX 12.0软件校核设计结果,其中湍流模型采用两方程的SST模型,转捩预测采用γ-Reθ转捩模型。

γ-Reθ转捩模型的基本思想是建立关于间歇因子γ和动量厚度雷诺数Reθ的标量输运方程,由应变率雷诺数Rev触发转捩,通过γ控制湍动能输运方程中的生成项,使其在流动转捩后再起作用,从而实现对边界层转捩的数值模拟[5]。CFX软件采用Menter发展的基于SST模型的γ-Reθ转捩模型进行层流转捩模拟,集合了转捩经验关系式和低雷诺数湍流模型的优势。文献[6]表明，该转捩模型可以有效预测机翼的转捩范围。

2.3 优化算法

气动设计经常需要处理多个目标问题。与单目标优化问题不同,多目标优化问题的解并不是唯一的,而是存在一个最优解集,即所谓的Pareto最优解集或非劣解集(Non-dominated)。Pareto最优解就是不存在比这个解方案中至少一个目标更好,而其他目标不低劣的更好的解[7]。由于多目标优化问题一般不存在单个最优解,因此设计人员希望得到Pareto最优解集(也称Pareto前沿),再根据最优解分布进行多目标决策。遗传算法是求解多目标优化问题的Pareto最优解集的有效方法。采用遗传算法进行多目标气动优化已有很多成功的案例[8-9]。

本文选择基于精英保留策略的非支配排序的多目标遗传算法(Nondominated Sorting Genetic Algorithm II,NSGA-II)作为优化算法。NSGA-II根据产生的各种非劣前沿,采用了一种快速的非支配排序方法,从而减小了算法运行的整体时间。NSGA-II使用了排挤算法来代替共享函数算法,无需确定一个共享参数就能控制个体的分布;并引入了精英保留策略,提高了种群的整体进化水平。在约束处理方面,NSGA-II算法加入了一种高效的约束处理机制,不需采用任何罚函数方法,而是通过引入一种虚拟的越界值,给所有的等式或不等式约束条件提供了一种通用的解决方案。NSGA-II算法操作简单,具有较好的收敛速度和全局搜索能力,已成为多目标优化领域的基准算法之一。

2.4 优化流程

优化设计流程如图2所示,兼顾了巡航点层流工况、湍流工况和最大升力系数工况(湍流状态)。

图2 多目标多约束优化设计流程Fig.2 Design progress for multi-objective and multi-constraint optimization

优化设计分2步:

第1步:以巡航工况层流升阻比、巡航工况层流俯仰力矩、低速最大升力系数为目标;以巡航湍流升力系数、俯仰力矩以及几何要求等为约束,进行翼型多目标多约束优化。

第2步:从第1步结果的Pareto前沿中筛选出一组结果,组成二次优化的初始种群。二次优化以巡航工况层流升阻比最大为目标,其余要求转化为约束。

3 设计结果

以Eppler432翼型为初始翼型(E432翼型),相对弦长厚度16%。图3为第1步优化的双目标Pareto前沿分布,可以发现巡航升阻比K和低速最大升力系数CLmax是相互矛盾的。翼型的最大升力系数要求大于1.4,但考虑计算误差和设计余量,这里选择CLmax大于1.5。CLmax大于1.5的结果均为可行解,即图3中分界线Line1以上部分。

将第1步最大升力系数目标调整为大于1.5的设计约束,从第1步优化的可行解中选择若干解组成第2步优化的初始种群,开始第2步优化设计。图4为第2步单目标优化收敛曲线,可以看到优化迭代已经收敛。由于采用XFOIL面元法程序,虽然迭代了近4 000步,但用时仅约3 h。

图4 单目标优化迭代曲线Fig.4 Iteration curve of single objective optimization

图5给出了优化翼型(OPT)与E432翼型的几何对比,优化翼型具有明显的前缘加载特征。图6为优化翼型与E432翼型在巡航设计点的压力分布对比。结果显示,优化翼型上表面层流区超过40%弦长,下表面层流区达到约80%弦长。

图5 优化翼型与初始翼型几何对比Fig.5 Geometry comparison between OPT airfoiland initial airfoil

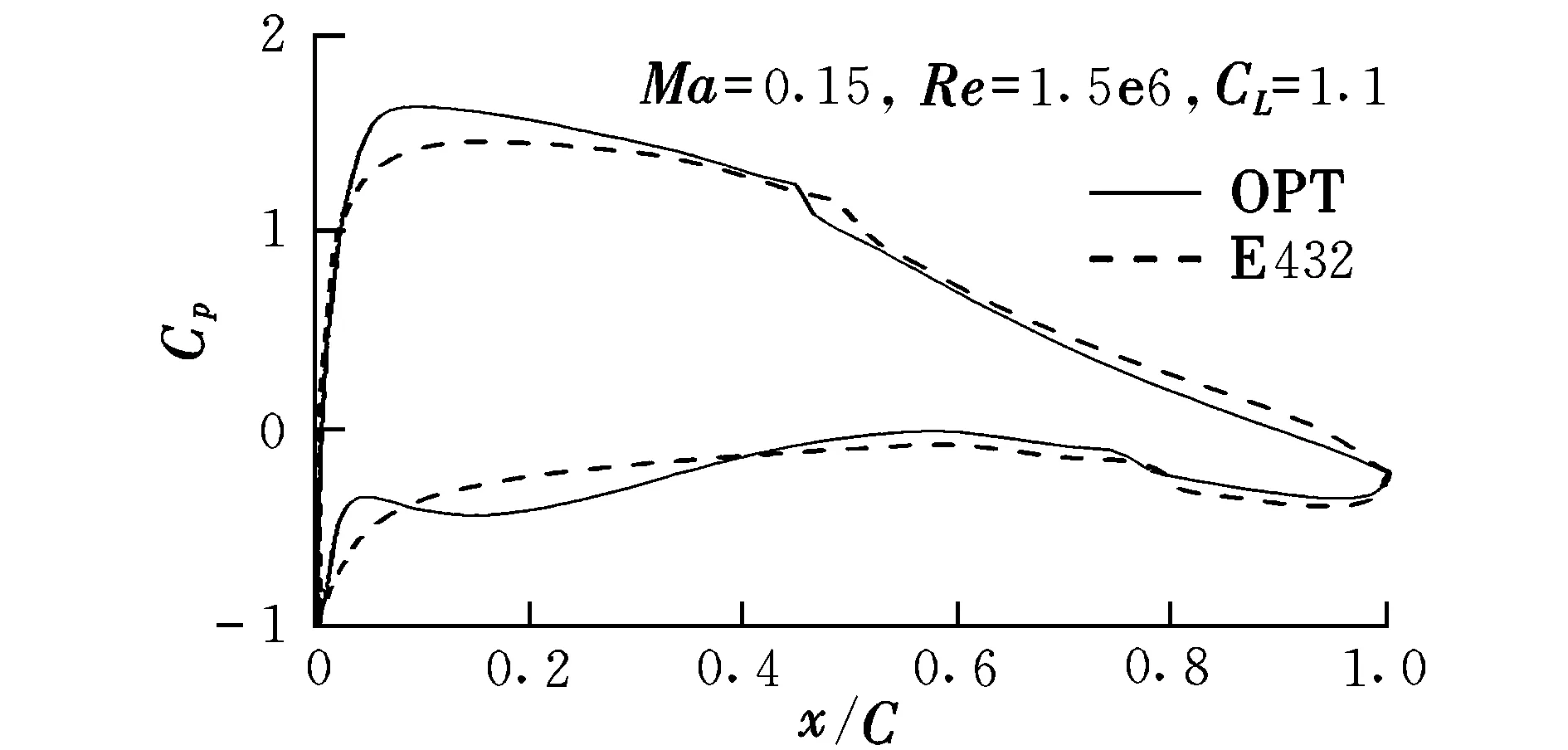
图6 翼型压力分布对比Fig.6 Comparison of Cp distribution

图7～图9为优化翼型与E432翼型按自由转捩计算的气动力对比曲线。由于优化翼型的层流区略小于E432翼型,其最大升阻比不及E432翼型;但优化翼型的大迎角分离特性和巡航工作状态的俯仰力矩特性都优于E432翼型。

图7 升力系数对比曲线Fig.7 Correlation curves of CL

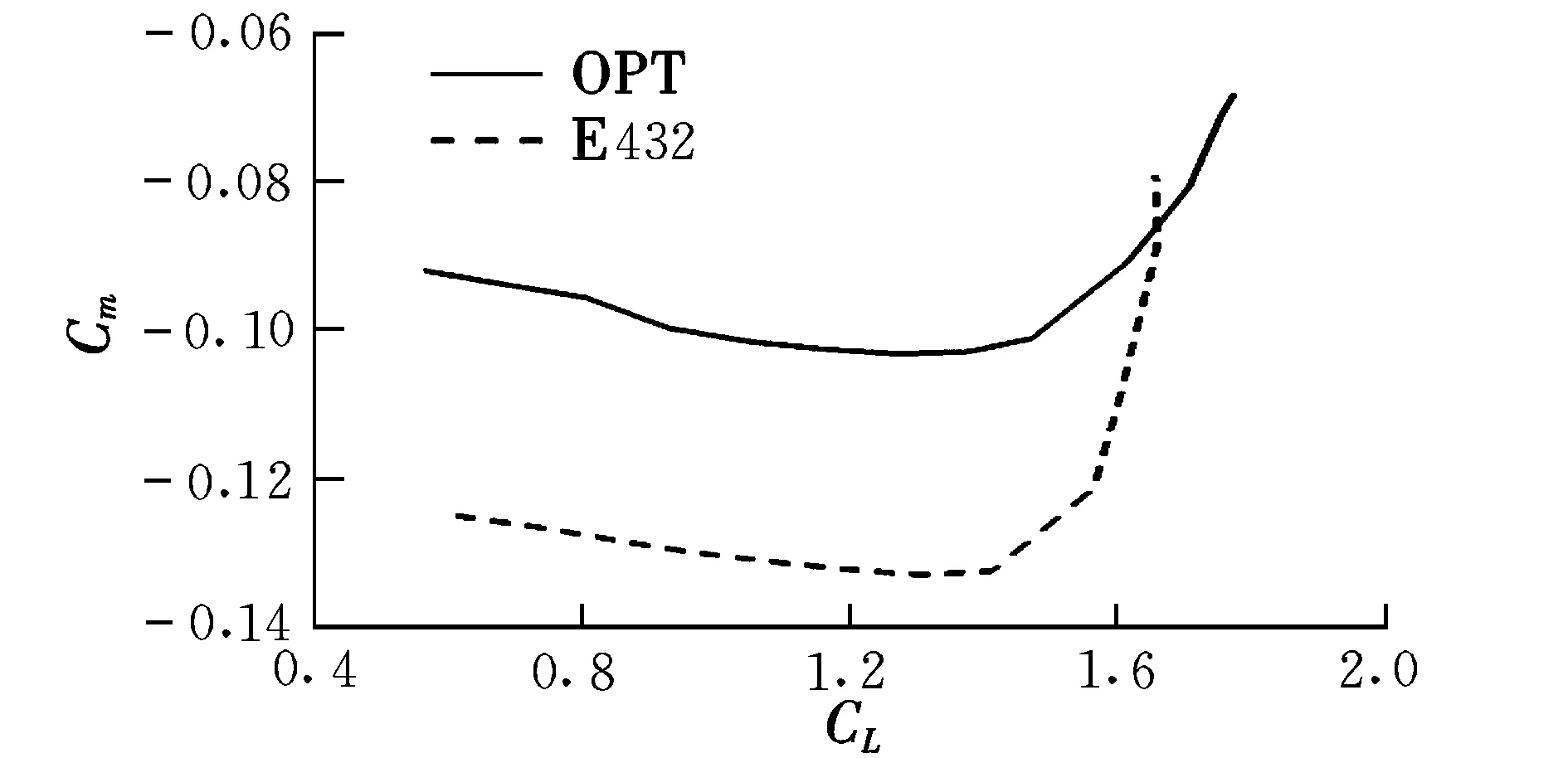
图8 俯仰力矩对比曲线Fig.8 Correlation curves of Cm

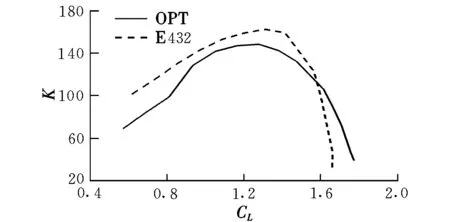
图9 升阻比对比曲线Fig.9 Correlation curves of K

4 校核分析

校核分析软件采用ANSYS-CFX 12.0,基于N-S方程求解,转捩预测采用γ-Reθ模型。分析工况:Ma=0.15,Re=1.5×106,α=0°～14°。结果如图10～图12所示。

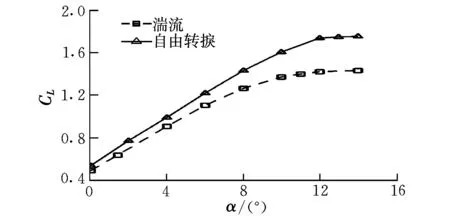
图10 升力系数曲线Fig.10 Curves of CL

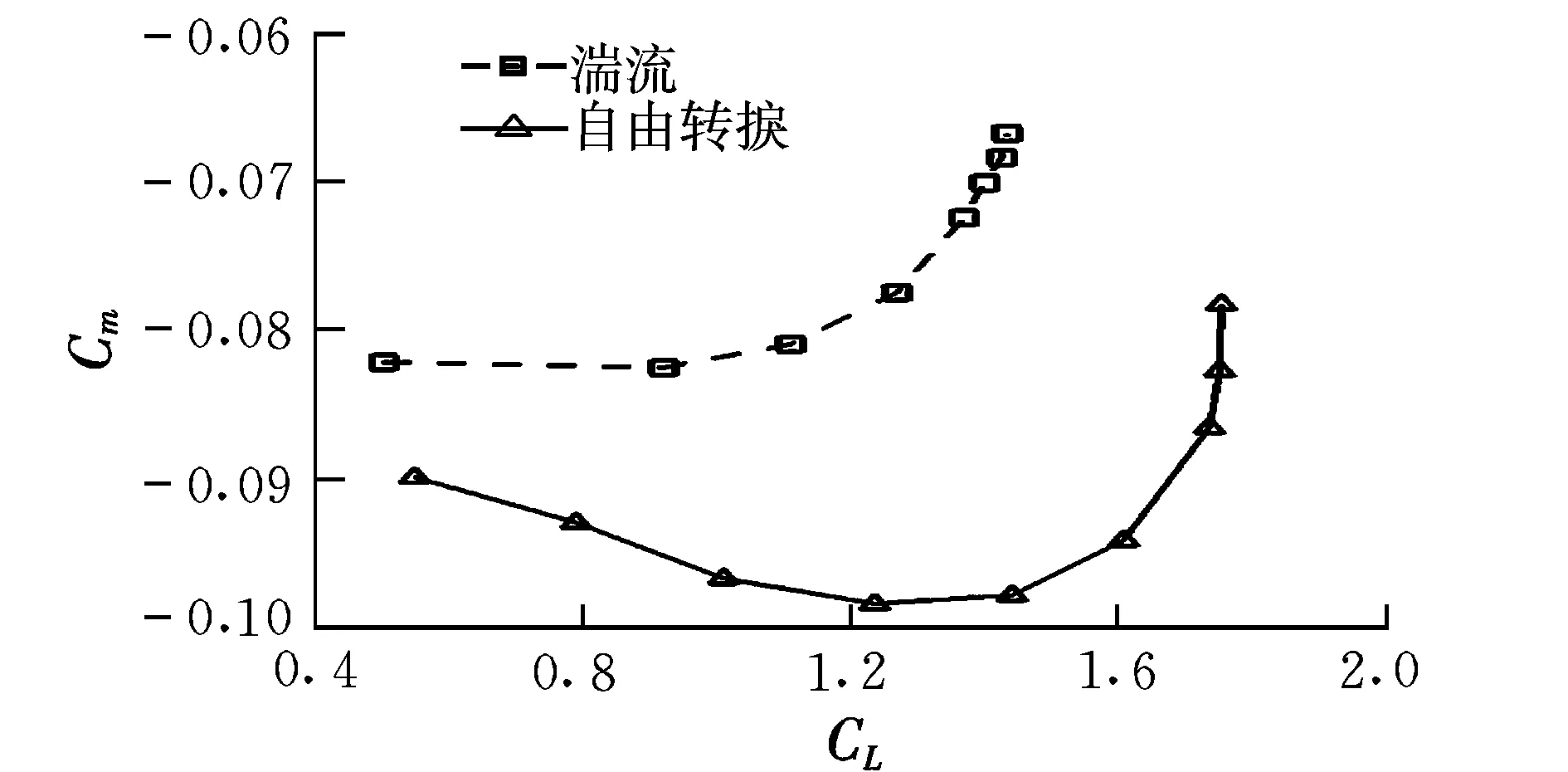
图11 俯仰力矩系数曲线Fig.11 Curves of Cm

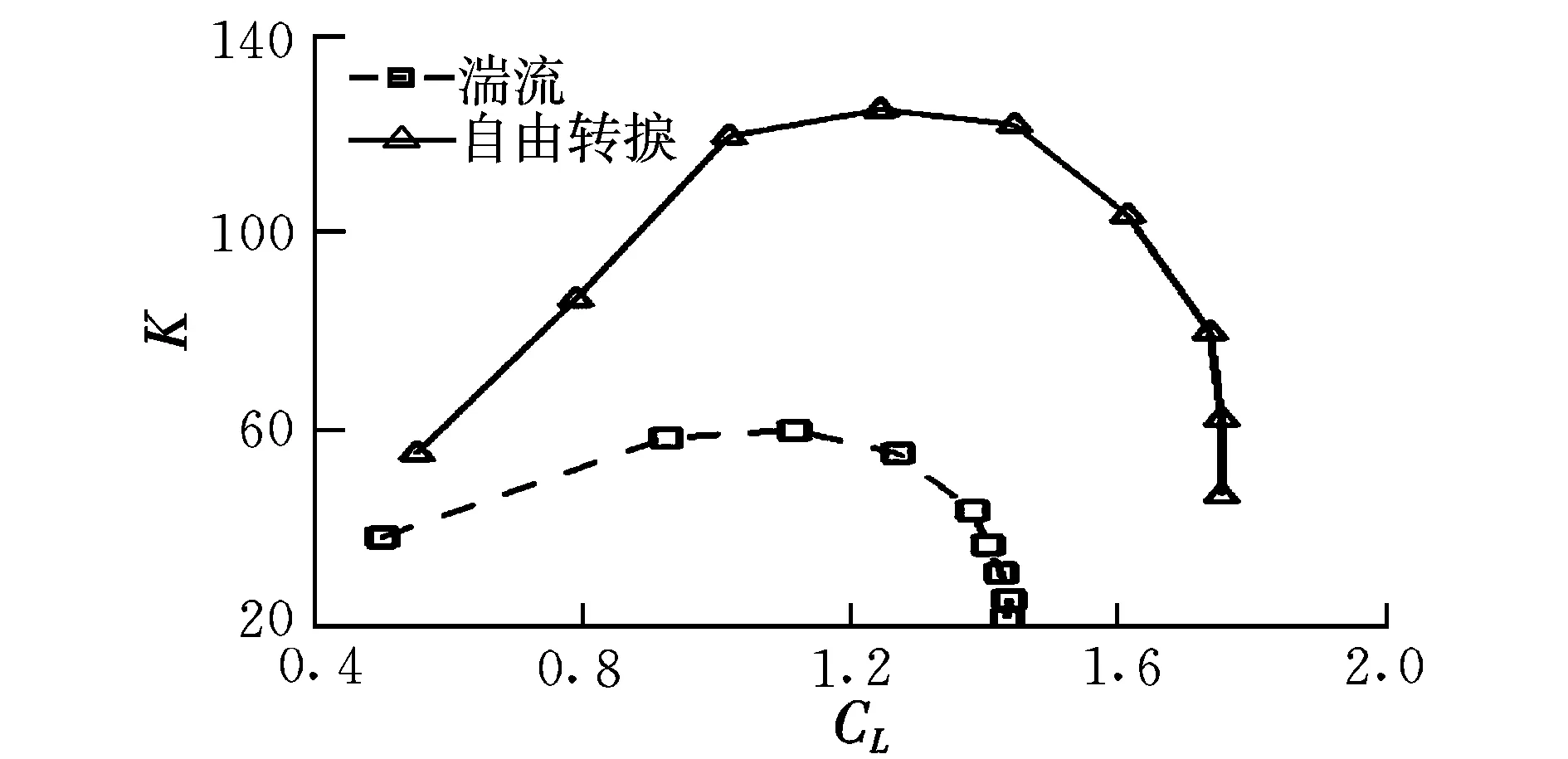
图12 升阻比曲线Fig.12 Curves of K

分析结果可以看出:

(1)设计点附近(CL=1.1),湍流相对于自由转捩,升力系数下降量在10%以内,满足设计要求;

(2)自由转捩条件下,翼型在设计点的升阻比约120,最大升阻比约128;湍流条件下翼型的最大升阻比仅约60;

(3)自由转捩条件下,设计点附近翼型的俯仰力矩大于-0.1,满足设计要求;

(4)自由转捩条件下,翼型失速迎角达到13°,最大升力系数约1.75;湍流条件下翼型失速迎角达到13°,最大升力系数超过1.4,满足设计要求。

综上所述,优化翼型满足设计要求。

5 结束语

优化翼型综合了高升力、层流和低力矩的要求,具有不因提前转捩引发飞行安全的能力及明显的前加载几何特性。本文方法具有良好的工程实用性。

参考文献：

[1] 冯密荣.世界无人机大全[M].北京:航空工业出版社,2004:207-208.

[2] Kulfan B M,Bussoletti J E.“Fundamental” parametric geometry representations for aircraft component shapes [R].AIAA-2006-6948,2006.

[3] 乔志德,吕晓斌.高Re数超临界自然层流翼型设计[R].西安:西北工业大学翼型研究中心,1989.

[4] 邱玉鑫,程娅红,胥家常.浅析高空长航时无人机的气动研究问题[J].流体力学实验与测量,2004,18(3):1-5.

[5] 符松,王亮.湍流转捩模式研究进展[J].力学进展,2007,37(3):409-416.

[6] Langtry R B,Menter F R.Transition modeling for general CFD application in aeronautics[R].AIAA-2005-522,2005.

[7] 崔逊学.多目标进化算法及其应用[M].北京:国防工业出版社,2008:40-56.

[8] 李倩,詹浩,朱军.基于Pareto遗传算法的机翼多目标优化设计研究[J].西北工业大学学报,2010,28(1):134-137.

[9] 王晓鹏.遗传算法及其在气动优化设计中的应用研究[D].西安:西北工业大学,2000.