一种离散直接自适应模糊滑模控制
张晓宇刘彬博
(1.华北科技学院 电子信息工程学院,北京 101601; 2. 中央新影集团 CCTV证券资讯频道,北京 100080)
模糊、自适应等方法在连续系统控制问题中已经显示出成功的运用[1-25]。但目前模糊直接、间接自适应等方法在离散系统中的运用研究尚不深入,有大量待研究、发展的问题。在离散系统中,由于系统的离散化以及系统的理想滑动模态根本不能到达,所以准滑动模态的降阶特性不再存在。这给系统的稳定性分析造成了困难。滑模控制的分步设计法虽然可以实施,但是不能保证较好的鲁棒稳定性。离散系统的采样时间对于模糊逻辑系统的逼近能力产生很大影响,对于自适应机构的自适应能力、速度也同样产生较大影响。因而离散系统中模糊自适应方法在滑模控制中的应用对于消除滑模控制的抖振作用较之连续系统大大减弱。
本文从自适应模糊逻辑系统出发用离散动态自适应模糊逻辑系统逼近滑模控制律,给出逼近误差收敛的自适应机构和构建方法;通过AFLS动态的参数设计形成较好的滤波效果,用以消除抖振。
1 离散非线性系统的SMC
考虑如下离散非线性系统,
(1)
式中:f(xi(k))、g(xi(k))满足
g(xi(k))=g+Δg(xi(k))

(2)
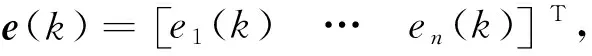
(3)
设滑模s(k)=CTe(k),C=[c1c2…cn-11]T∈Rn是Hurwitz多项式的系数。对于上述线性不确定离散系统提出以下定理。
定理1 对于非线性系统(1),若取准滑模控制律
r(k)+(qT1-1)s(k)+k2sgns(k)]
(4)
式中:T1为准滑模控制器的采样周期。设计参数q、k2满足
(5)

证明考虑不等式离散到达条件
(6)
Δsk+1=sk+1-sk=f(xi(k))+Δgusk-
(qT1-1)sk-k2sgnsk-sk
(qT1-1)sk-k2sgnsk]
(7)
[Δsk+1]2=[f(xi(k))+Δgusk-(qT1-1)sk-k2sgnsk]2+
(8)
若要使得到达条件(6)满足,将式(7)、(8)代入式(6)得
(1+Δgg-1)|(qT1-1)sk|+(1+Δgg-1)k2
(9)
依据式(5)式(9)等价为
可见在边界Δ外到达条件(6)成立。证毕。
定理1虽然得到了系统(3)的一个SMC,但是这个SMC使得滑模到达切换带是很宽的,而且宽度随着系统不确定性的变化而变化。这在实际上会形成很大的抖振。因此本文寻求其模糊自适应SMC以消除抖振。
2 模糊自适应SMC
对于定理1准滑模控制率,引入滑模边界层参数λ>0,当系统滑模到达边界层内施加模糊逻辑(FLC)控制律uf(k),停止准滑模控制率us(k)。即
u(k)=us(k)+uf(k)
式中:uflc是模糊逻辑系统的输出,Δ是准滑动模态区的宽度,因此λ≥Δ。
边界层厚度参数λ的范围与系统不确定动态非线性函数的上界有直接关系。非线性系统的不确定性越大,准滑动模态区宽度越大,参数λ选择范围越大。实验证明λ对每个具体非线性系统有一个最佳值。可以通过以下方法选择:已知状态的初始值,代入非线性函数上界得到Δ值。一般λ∈[Δ,3Δ]效果较好。
2.1 自适应模糊逻辑系统
对于系统(1)用AFLS来逼近滑模控制律。所采用的AFLS与文献[17]中相同,后件参数采用梯度优化自校正的方法进行。
选择滑模s(k)以及Δs(k)为输入变量,构造具有2个输入变量、1个输出变量的FBF型AFLS。其中的前件参数由设计者调节,后件参数由自适应机构校正。模糊控制规则为
Ri: Ifs(k) issiandΔs(k) isΔsithenuf(j) isθi(j)
i=1,2,…,m
式中:α为滑模s(k)的划分参数,β为滑模变化率,Δs(k)的划分参数,j是AFLS的采样步长,θi(j)是待校正的后件参数,m是规则总数。采用单点模糊化、乘积推理、加权平均解模糊方法滑模控制的模糊逼近输出为
uf(j)=θ(j)Tp
(10)
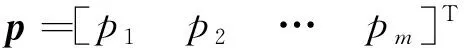

2.2 自适应率
定义自适应模糊逻辑系统(AFLS)逼近滑模控制律(4)的误差目标函数为
这样AFLS逼近控制律(4)的问题就转化为目标函数J(θ,x)的优化问题。即
求目标函数沿参数θ方向的梯度得
参数θ自校正的方向应该沿着目标函数对其梯度的负方向,由式(11)确定θ的校正方向,
θ(j+1)-θ(j)=p(u(k)-θT(j)p)
(11)
2.3 DAFLS逼近滑模控制
先考虑T1=lT2,l∈Ζ的情况下,AFLS输出(10)逼近普通离散SMC的误差。
定理2 对于准滑模控制(4),若AFLS以式(11)为自适应机构且其采样周期T2远比准滑模控制(4)的采样周期T1小,则AFLS(10)逼近准滑模控制(4)的误差渐近收敛。
证明在自适应律(11)下选取逼近误差的Lyapunov函数为
(12)
若AFLS的采样周期远比控制器u(k)的采样周期小则对式(12)有
利用式(11)有
pTp(u(k)-θ(j)Tp)θ(j)Tp-pTp(u(k)-θ(j)Tp)·
pTp(u(k)-θ(j)Tp)2
(13)
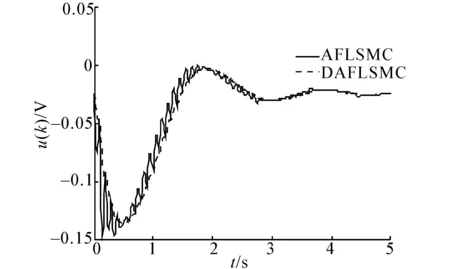
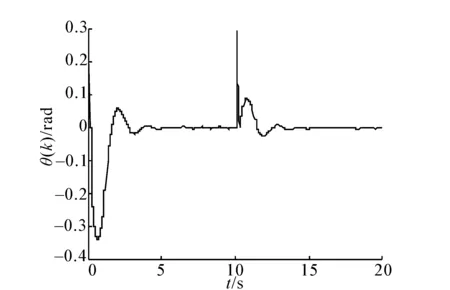
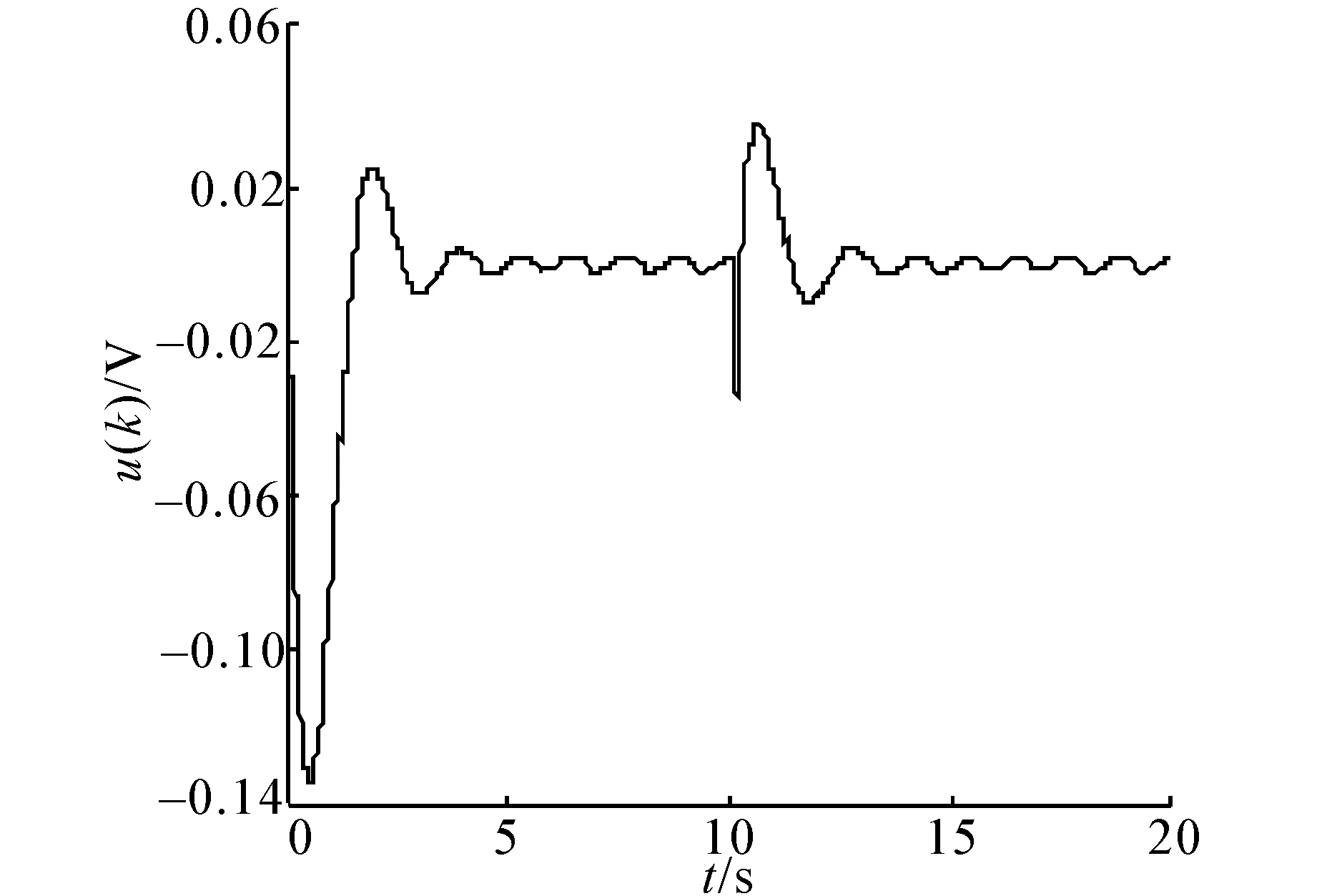
因为p是模糊基函数向量,所以0 Δv(j)=v(j+1)-v(j)<0 证毕。 接着,为进一步加强滤波效果以消除抖振,在AFLS基础上引入动态自适应模糊逻辑系统(dynamic adaptive fuzzy logic system, DAFLS)。 考虑n阶连续DAFLS,则 (14) 式中:di(i=0,1,…,n-1)、γ均为DAFLS的动态参数。 假设(14)的动态形成低通滤波。将其离散化得到离散的DAFLS, v(k)[r0+r1z-1+…+rnz-n]=ωθTp (15) 式中:ri(i=0,1,…,n)、ω是导出的参数。运用DAFLS逼近滑模控制式(4)。 将滤波器(式(14))看作一个子系统,可以通过选择状态变量,将式(15)变为状态空间模型, (16) 式中:θTp看作是子系统(16)的输入,v(j)是这个子系统的输出。定理2已经证明如果没有引入滤波器动态,AFLS逼近滑模控制的误差是收敛的。现在选取新的关于其输出v(j)与滑模控制之间误差的正定Lyapunov函数,其一阶差分负定,则DAFLS的输出v(j)在适当的自适应律下逼近滑模控制的误差仍然收敛。DAFLS中的动态滤波器可以看作是线性系统(16)。 定理3 对于准滑模控制(4),若DAFLS(16)以(11)为自适应机构且其参数满足:ATCTCA半负定,Cb=1,采样周期T2远比准滑模控制(4)的采样周期T1小,则DAFLS(16)逼近准滑模控制(4)的误差渐近收敛。 证明选取逼近误差的Lyapunov函数为 其一阶差分为 ΔV(j)=1/2({[CAη(j)]2+[CbθT(j)p])2- [Cη(j)]2+2CAη(j)CbθT(j)p}+ Cη(j)θT(j)p-θT(j+1)pCAη(j)- θT(j+1)pCbθT(j)p+ 1/2({[θT(j+1)p]2-[θT(j)p]2})+ [θT(j+1)p]2-[θT(j)p]2+ 2us(k)[θ(j)-θ(j+1)]Tp= 1/2({[CAη(j)]2+[CbθT(j)p])2- [Cη(j)]2}+CAη(j)CbθT(j)p+Cη(j)θT(j)p- θT(j+1)pCAη(j)-θT(j+1)pCbθT(j)p+ 2us(k)[θ(j)-θ(j+1)]Tp 若代入θ(j+1)-θ(j)=p(u(k)-θT(j)p),有 [Cη(j)]2}+Cη(j)θT(j)p- [θT(j)p]2Cb-θT(j)pCAη(j)(1-Cb)- pTp(us(k)-θT(j)p)·(CAη(j)+CbθT(j)p)+ 3θT(j)p[us(k)-θT(j)p]pTp- 2us(k)[us(k)-θT(j)p]pTp (17) 若Cb=1,式(17)变为 若矩阵A、C满足Lyapunov方程 ATCTCA-CTC=-Q 其中Q=QT,Q>0。则有[CAη(j)]2≤[Cη(j)]2则 ΔV(j)≤2[(pTp)2-pTp][us(k)-θT(j)p]2 又因为p是模糊基向量则pTp≤1 。因此有ΔV(j)≤0成立。若ΔV(j)≡0成立则有 v(j)=us(k)=θT(j)p 成立。根据Lyapunov理论逼近误差收敛。证毕。 定理4 对于准滑模控制(4),若DAFLS(16)以(11)为自适应机构且其参数且满足定理2内容,则滑模到达条件(6)能够得到满足。 证明考虑不等式离散到达条件, Δsk+1=sk+1-sk=Δf+Δgufk-(qT1-1)sk- k2sgnsk+g(ufk-usk)-sk (qT1-1)sk-k2sgnsk+g(ufk-usk)] [Δsk+1]2=[Δf+Δgufk-(qT1-1)sk- 2sk[Δf+Δgufk-(qT1-1)sk- k2sgnsk+g(ufk-usk)] 若要使得到达条件满足,将skΔsk+1、[Δsk+1]2代入得 (18) 由式(18)可见,只要ufk逼近usk误差为零则与(9)是等同的。证毕。 一阶倒立摆系统的离散模型如下: 式中:θ(k)是摆角位移,u(k)是小车控制电压。 当应用普通SMC方法控制和应用本文提出的控制方法时得到摆角位移曲线对比如图1所示,控制电压曲线对比如图2所示。 图1 SMC和DAFLSMC控制下摆角位移曲线对比Fig.1 Angle displacement contract curves of pendulum for SMC and DAFLSMC 图2 SMC和DAFLSMC控制下电压曲线对比Fig.2 Control voltage contract curves for SMC and DAFLSMC 通过图1、2可以得出,普通离散SMC稳态抖动很大,而本文提出的DAFLSMC消除了抖动。比较DAFLSMC控制电压曲线与在同等条件下实施普通SMC的控制电压曲线,如图2。因为设计的DAFLS逼近SMC的采样时间是0.01 s而被控对象及普通SMC采样时间是0.1 s。因此DAFLS输出的控制电压更加光滑。 为了观察DAFLS的滤波效果把滤波前后的控制电压曲线作对比如图3所示。从图3中可见加入了动态滤波的DAFLS后控制信号的高频抖动部分被滤掉了。 图3 滤波器前后的控制电压曲线对比Fig.3 Control voltage comparison of AFLSMC and DAFLSMC 为验证本文所提出方法的鲁棒性能,保持控制器参数不变的情况下,在仿真t=10 s时,给摆角位移施加幅度为0.3 rad的脉冲干扰,系统控制效果如图4、图5所示。可见,在较强干扰施加给摆角时,系统仍然能够稳定回到原点,稳态性能不变。说明本文提出方法的确保留了普通离散SMC的鲁棒性。 图4 DAFLS控制下摆角位移受扰曲线Fig.4 The angle excursion curve when disturbed under DAFLSMC control 图5 DAFLS控制下受扰时控制电压曲线Fig.5 The control volt curve when disturbed under DAFLSMC control 提出了一种离散直接自适应模糊滑模控制方法。通过用AFLS逼近离散滑模控制,消除了SMC的抖振。逼近SMC的AFLS中必须引入动态,才能实现滤波功能,而且,动态AFLS采样时间要比系统采样时间小。通过与普通离散SMC的应用仿真对比,证明了该方法通过适当参数设置,不但保证了滑模到达,消除了SMC的抖振,还保留了SMC很强的鲁棒性能。该方法对离散SMC的应用具有一定价值,需进一步加强其在实际控制系统中的应用研究。 参考文献: [1]李继超,管萍,刘小河.间接自适应模糊滑模控制在电弧炉中的应用[J].系统仿真学报, 2009, 21(2): 542-546. LI Jichao, GUAN Ping, LIU Xiaohe. Application of indirect adaptive fuzzy sliding mode control in arc furnace[J]. Journal of System Simulation, 2009, 21(2): 542-546. [2]刘姗梅,马迁,陈贤顺,等.自适应模糊滑模控制在PMSM中的应用[J].微电机, 2009, 42(5): 43-46, 87. LIU Shanmei, MA Qian, CHEN Xianshun, et al. Application of adaptive fuzzy sliding mode controller in PMSM[J]. Micromotors, 2009, 42(5): 43-46, 87. [3]张向文,王飞跃.汽车ABS自适应模糊滑模控制算法研究[J]. 汽车技术, 2009, 40(10): 25-30. ZHANG Xiangwen, WANG Feiyue. Study on adaptive fuzzy sliding mode control algorithm for the vehicle ABS[J]. Automobile Technology, 2009, 40 (10): 25-30. [4]董小闵,余淼,廖昌荣,等. 具有非线性时滞的汽车磁流变悬架系统自适应模糊滑模控制[J]. 振动与冲击, 2009, 28(11): 55-60, 203. DONG Xiaomin, YU Miao, LIAO Changrong, et al. Adaptive fuzzy sliding mode control for magneto-rheological suspension system considering nonlinearity and time delay[J]. Journal of Vibration and Shock, 2009, 28(11): 55-60, 203. [5]高文达,方一鸣,张文亮,等. 自适应模糊滑模控制在伺服电动机系统中的应用[J]. 微特电机, 2009, 37(11): 32-36. GAO Wenda, FANG Yiming, ZHANG Wenliang, et al. Application of adaptive fuzzy sliding mode control to servomotor system[J]. Micromotors, 2009, 37(11): 32-36. [6]张金萍,刘阔,林剑峰,等.挖掘机的4自由度自适应模糊滑模控制[J].机械工程学报, 2010, 46(21): 87-92. ZHANG Jinping, LIU Kuo, LIN Jianfeng, et al. 4-DOF adaptive fuzzy sliding mode control of excavator[J]. Journal of Mechanical Engineering, 2010, 46(21): 87-92. [7]王宏伟,井元伟,于驰.基于自适应模糊滑模控制的主动队列管理算法[J].系统仿真学报, 2008, 20(23): 6330-6332, 6342. WANG Hongwei, JING Yuanwei, YU Chi. Active queue management algorithm based on adaptive fuzzy sliding mode control[J]. Journal of System Simulation, 2008, 20(23): 6330-6332, 6342. [8]赵红超,徐君明,王东.变质心弹头的自适应模糊滑模控制[J]. 清华大学学报:自然科学版, 2008, 48(S2): 1733-1736. ZHAO Hongchao, XU Junming, WANG Dong. Adaptive fuzzy sliding mode control for mass motion warhead[J]. Journal of Tsinghua University: Science and Technology, 2008, 48(S2): 1733-1736. [9]彭亚为,陈娟,刘占富, 等. 自适应模糊滑模控制在化工过程中的应用[J].化工学报, 2012, 63(9): 2843-2850. PENG Yawei, CHEN Juan, LIU Zhanfu, et al. Adaptive sliding mode control in chemical process application[J]. Journal of Chemical Industry and Engineering, 2012, 63(9): 2843-2850. [10]刘金琨.滑模变结构控制MATLAB仿真[M]. 北京:清华大学出版社, 2005:32-36. [11]GUO Liping, HUNG J Y, NELMS R M, et al. Comparative evaluation of sliding mode fuzzy controller and PID controller for a boost converter[J]. Electric Power Systems Research, 2011, 81(1): 99-106. [12]POURSAMAD A, DAVAIE-MARKAZI A H. Robust adaptive fuzzy control of unknown chaotic systems[J]. Applied Soft Computing, 2009, 9(3): 970-976. [13]HSU C F, CHUNG I F, LIN C M, et al. Self-regulating fuzzy control for forward DC-DC converters using an 8-bit microcontroller[J]. IET Power Electonics, 2009, 2(1): 1-13. [14]TU K Y, LEE T T, WANG W J. Design of a multi-layer fuzzy logic controller for multi-input multi-output systems[J]. Fuzzy Sets and Systems, 2000, 111(2): 199-214. [15]LIN W S, CHEN C S. Sliding-mode-based direct adaptive fuzzy controller design for a class of uncertain multivariable nonlinear systems[C]//Proceedings of the American Control Conference. Anchorage, Alaska, USA, 2002: 2955-2960. [16]WAI R J, LIN C M, HSU F. Self-organizing fuzzy control for motor-toggle servomechanism via sliding mode technique[J]. Fuzzy Sets and Systems, 2002, 131(2): 235-249. [17]ZHANG X Y, SU H Y, CHU J. Adaptive sliding mode-like fuzzy logic control for high-order nonlinear systems[C]//Proceedings of the 2003 IEEE International Symposium on Intelligent Control. Houston, Texas, USA, 2003: 788-792. [18]HWANG C L, WU H M, SHIH C L, et al. Fuzzy sliding-mode underactuated control for autonomous dynamic balance of an electrical bicycle[J]. IEEE Transactions on Control Systems Technology, 2009, 17(3): 658-670. [19]WANG W, LIU X D. Fuzzy sliding mode control for a class of piezoelectric system with a sliding mode state estimator[J]. Mechatronics, 2010, 20(6): 712-719. [20]HO T H, AHN K. Speed control of a hydraulic pressure coupling drive using an adaptive fuzzy sliding-mode control[J]. IEEE/ASME Transactions on Mechatronics, 2012, 17(5): 976-986. [21]YAU H T, WANG C C, HSIEH C T, et al. Nonlinear analysis and control of the uncertain micro-electro-mechanical system by using a fuzzy sliding mode control design[J]. Computers and Mathematics with Applications, 2011, 61(8):1912-1916. [22]ZHU M C, LI Y C. Decentralized adaptive fuzzy sliding mode control for reconfigurable modular manipulators[J]. International Journal of Robust and Nonlinear Control, 2010, 20(4): 472-488. [23]SHAHRAZ A, BOOZARJOMEHRY R B. A fuzzy sliding mode control approach for nonlinear chemical processes[J]. Control Engineering Practice, 2009, 17(5): 541-550. [24]HO H F, WONG Y K, RAD A B, et al. Adaptive fuzzy sliding mode control with chattering elimination for nonlinear SISO systems[J]. Simulation Modelling Practice and Theory, 2009, 17(7): 1199-1210. [25]PALM R. Sliding mode fuzzy control[C]//Proceedings of IEEE International Conference on Fuzzy Systems. San Diego, CA, USA, 1992: 519-526.3 主要结果
3.1 动态AFLS的逼近误差
3.2 近似逼近下的滑模可达性
4 倒立摆系统应用仿真
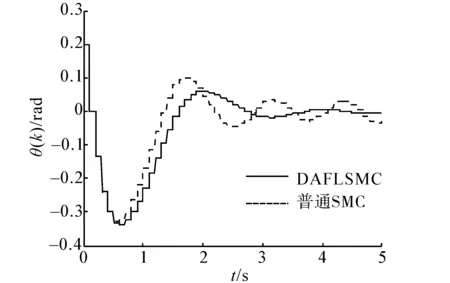
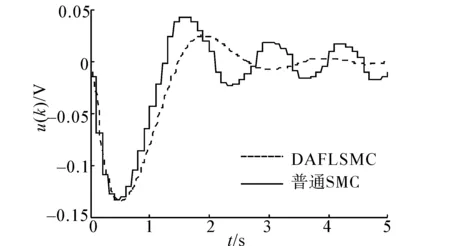
5 结束语

