基于四元数的欠驱动AUV的镇定控制设计

吴琪, 李晔

(哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001)

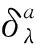
1 四元数

四元数向量写法为

Q=t+xi+yj+zk

以原点为旋转中心，旋转的轴分别是α、β、γ(α2+β2+γ2=1)，用右手系的坐标定义，望向向量α、β、γ的前进方向反时针旋转θ，用四元数表示为[4]

在大地坐标系和联体坐标系中，当给定物体的姿态用φ、θ、φ表示，并且分别以x、y、z旋转，则实现从四元数到欧拉角的转换公式为[5]

θ=arcsin[-2(q1q3-q0q2)]

式中：φ、θ、φ分别为横滚角、纵倾角和偏航角，q0、q1、q2、q3分别为四元数的各个分量。实现上述坐标转换的方向余弦矩阵为

Abg=Ax(φ)Ay(θ)Az(φ)=

实现相应坐标转换的四元数矩阵为

2 水下机器人空间运动方程

水下机器人6自由度空间运动方程可以写为[1]

(1)

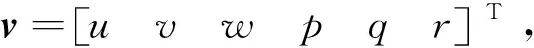
欠驱动水下机器人一般采用桨—舵—翼形式，因此外部作用力轴向推进力τ1、横滚力矩τ4、纵倾力矩τ5和偏航力矩τ6，忽略二阶非线性水动力细数的影响，将方程(1)展开为式(2):

w(cosφsinθcosφ+sinφsinφ)

w(sinφsinθcosφ-cosφsinφ)

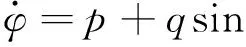
(Xu/m11)u]

(2)

为了获得合适的同类型的运动模型，选择单位四元数来参数化模型(2)，单位四元数定义为：在单位向量k附近旋转角度φ，则4个参数有如下形式：

ε4=cos(φ/2)

假设|φ|<π，且ε4>0，单位四元数满足：

(3)

方程(2)可以写为

(Xu/m11)u]

(Yv/m22)v]

(Zw/m33)w]

(4)

定义向量η=[η1η2]T，其中η1=[xyz]T是惯性坐标系下的位置向量，η2=[ε1ε2ε3]T。定义τ=[τ1τ2τ3τ4τ5τ6]T分别代表纵向、横向、垂向、横滚、纵倾、首摇方向的控制输入。

3 AUV的镇定设计

这一部分只考虑AUV的镇定控制输入只有4个方向：轴向推进力τ1、横滚力矩τ4、纵倾力矩τ5和偏航力矩τ6。根据Brockett定理的第3个条件[6]，可知六自由度空间运动方程不存在任何光滑时不变反馈控制使系统在平衡点附近渐进稳定。因此本文提出一个连续时变反馈控制律。

考虑虚拟设计控制输入：

ud(η,ε,v,w,t)=-kxx+

ρa(η,ε,v,w)sin(t/ε)

(5)

pd(η,ε,v,w,t)=-kε1ε1

(6)

qd(η,ε,v,w,t)=-kε2ε2-2(kz+

(7)

rd(η,ε,v,w,t)=-kε3ε3+2(ky+

(8)

式中：kx、kε1、kε2、kε3、k、d、ε均大于零。ρa(η,ε,v,w)是一个任意可微的同类型的标准函数[3]，考虑到其形式为

(λx,λ2y,λ2z,λε1,λε2,λε3,λ2v,λ2w,t)

进一步定义控制输入：

τ1(η,v,t)=-k1m11(u-ud(η,v,w,t))

(9)

τ4(η,v,t)=-k4m44(p-pd(η,v,w,t))

(10)

τ5(η,v,t)=-k5m55(q-qd(η,v,w,t))

(11)

τ6(η,v,t)=-k6m66(r-rd(η,v,w,t))

(12)

则存在ε0>0，对于任意的ε∈(0,ε0)，当k1、k2、k3、k4足够大且全为正数，则控制律(9)～(12)可使系统(4)局部指数镇。考虑如下的形式：

(λx,λ2y,λ2z,λε1,λε2,λε3,λ2v,λ2w,t)

证明：AUV的空间运动方程模型(1)在控制输入τ2=0,τ3=0的情况下，可写为

(13)

式中：

(14)

由于ε4没有包含在f(η,v,t)中，且ε4可由式(11)惟一定义，因此可以将系统(14)中的第7个方程去除。如果简化后的方程局部渐进稳定，则原系统方程(13)也渐近稳定。

(15)

方程组(5)～(8)定义了(15)的控制输入。鉴于其是周期时变输入，因此产生的系统结果也是周期时变的，可写为

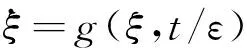
(16)

取用自治的平均系统近似的代替系统(16)，方程(16)的平均系统为

式中：g0(ξ)是其平均值。将控制输入(13)～(16)带入到(15)，系统(15)的平均系统可写为

(17)

方程(17)可以写成如下的级联系统：

(18)

(19)

根据线性理论知识容易得到式(19)是全局稳定的。当系统(19)全局稳定时，其状态向量全部趋近于零。且由(18)可以看出，关联项是高阶小的形式，因此只要设计证明系统(18)的名义系统稳定即可。根据Hurwitz稳定性定理，当名义系统矩阵的所有特征值具有负实部，则系统可以实现稳定。因此根据文献[4]命题，存在k1、k2、k3、k4足够大且全为正数，合理地选择参数k、d，能够使得系(18)渐近稳定。

4 镇定仿真

AUV的基本参数为[7]：m11=215，m22=265，m33=265，m44=40，m55=80，m66=80，d11=70，d22=100，d33=100，d44=30，d55=50，d66=50，且AUV是中性浮力，不计入重力和浮力(假设重力和浮力平衡，且重心浮心重合)。

采用式(9)～(12)的控制律进行控制输入，从上一节可知τ4=0，满足渐近收敛。相关控制参数如下：k1=3，k5=3，k6=3，kx=2，kε2=2，kε3=2，k=0.3，d=0.3，ε=2.5，名义准则取为

(30)

初始位置为

仿真结果如图1～6所示，图1表示平移速度u、v、w变化情况，图2表示转动角速度p、q、r的变化情况，图3表示位移x、y、z的变化情况，图4表示转换变量ε1、ε2、ε3曲线，图5反映机器人的实际镇定运动轨迹，图6代表名义标准ρα变化曲线。

图1 平移速度u、 v、 wFig.1 Velocity of vehicle u, v, w

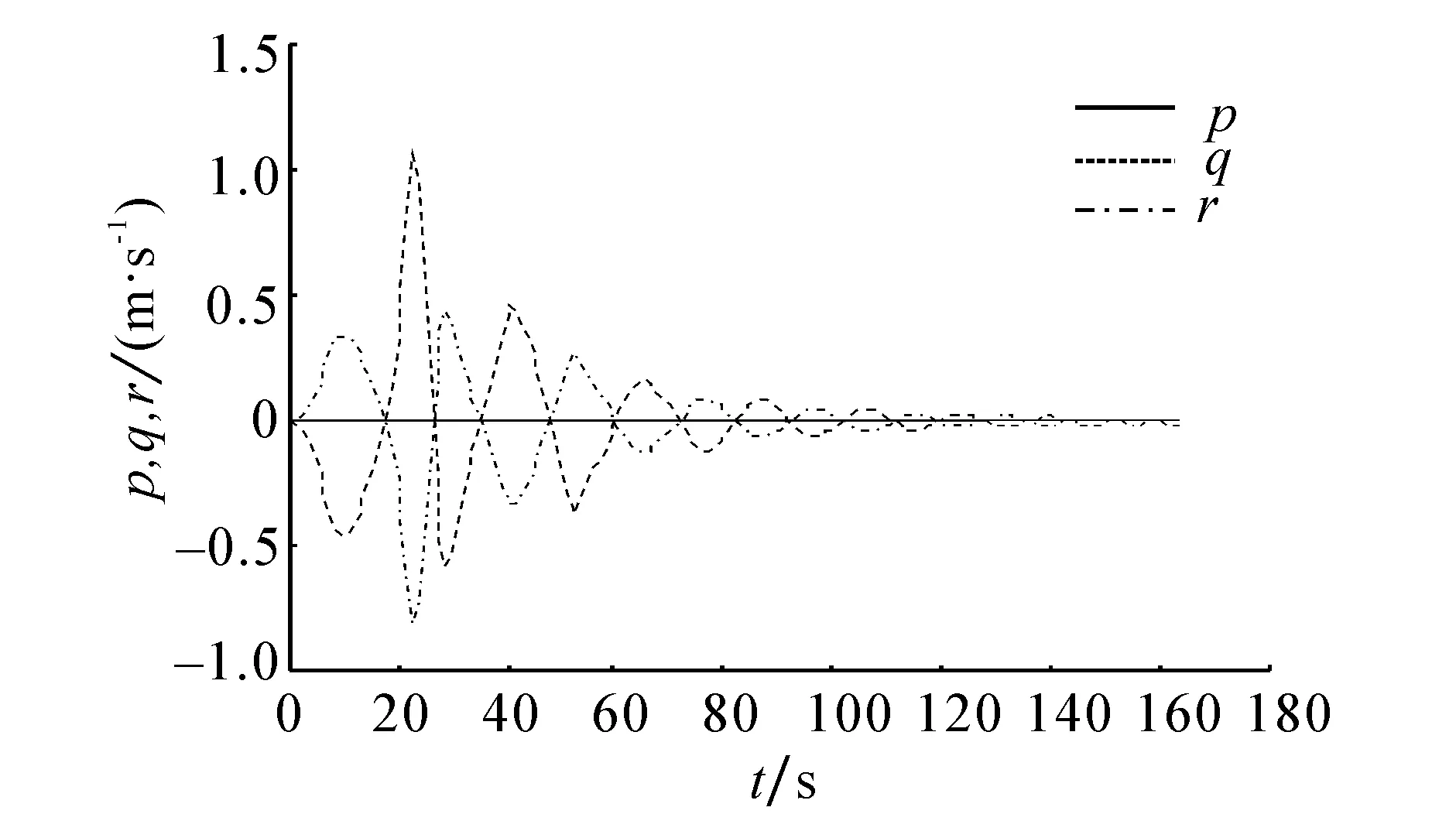
图2 旋转速度p、 q、 rFig.2 Rotational speed of vehicle p, q, r

图3 位移x、y 、zFig.3 Displacement of vehicle x, y, z

图4 转换变量ε1,ε2、ε3 Fig.4 Transformation variables ε1,ε2,ε3

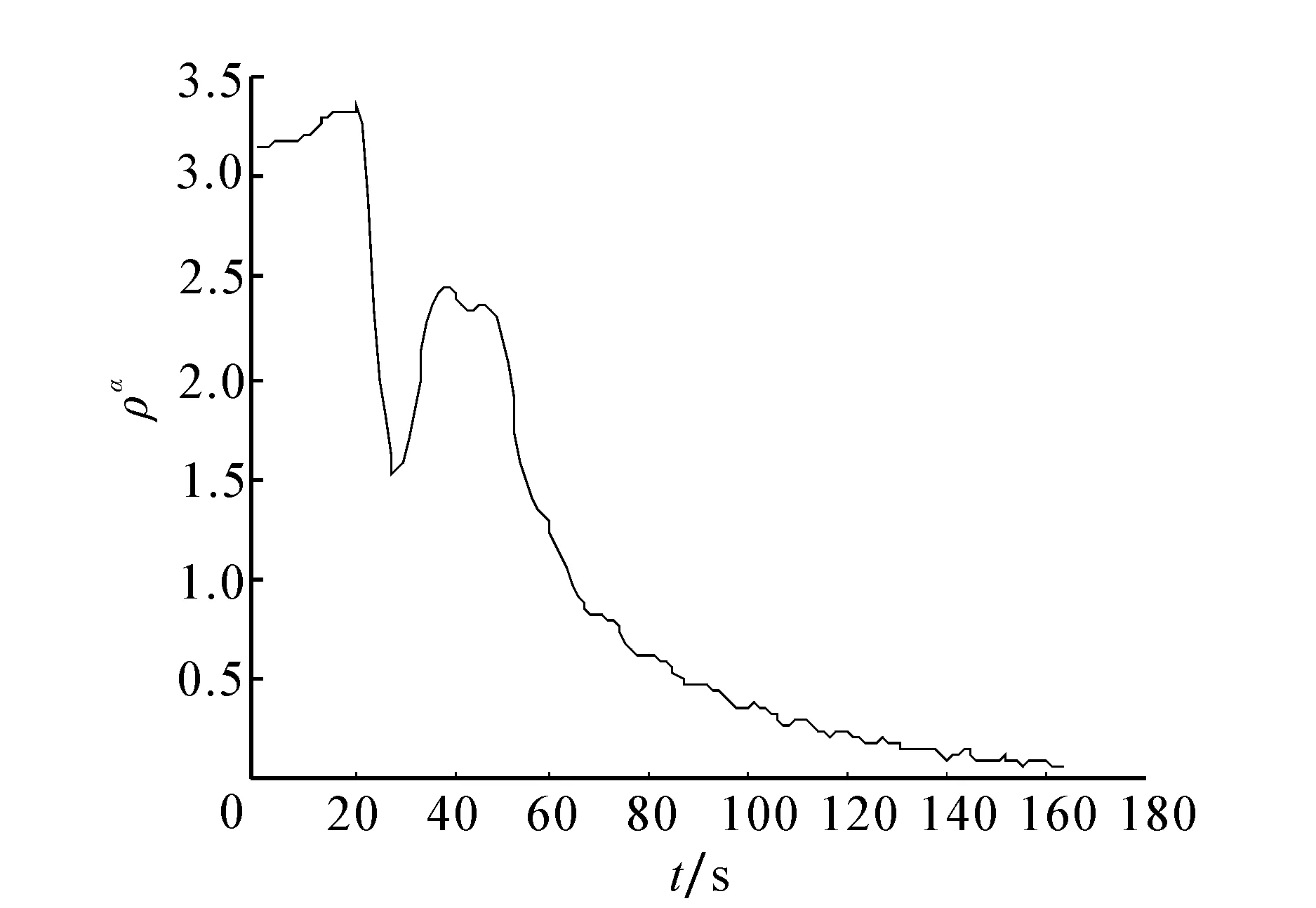
图5 实际轨迹图Fig.5 Actual path of vehicle

图6 名义标准ρα响应Fig.6 Response of the dilation ρα

图1中速度在初始时刻具有较大的变化率和超调量，说明初始时刻有较大的控制输入以及输入变化，即输入的力和力矩是突然加入的，引起欠驱动AUV有较大的速度变化，在仿真中这是允许的。位移图3在稳定点附近存在震荡，因此实际的运动轨迹在稳定点附近会比较密集，仿真结果与此相符合。因此在实际的AUV操控中，就需要考虑物理量的变化快慢，不能急剧地改变AUV的运动参数，使得AUV发生抖动，影响实际的轨迹跟踪。

由图1可以看出，纵向速度相比于横向和垂向速度收敛较慢，图3中纵向位移相比于横向和垂向位移收敛也较慢，因为纵向存在控制输入，而控制输入是各个变量的综合函数，其收敛要滞后于单个变量，因此纵向方向的变量收敛会比较慢。

转换变量ε1、ε2、ε3代表了横滚、纵倾、首摇的角速度，由于初始控制输入的较大加入，其变化震荡也比较明显，与平移速度相一致需要考虑实际情况的变化快慢。名义标准ρα是各个变量的偶次方之和，因此必大于零，随着各个变量的收敛到零，ρα必趋于零。初始时刻其变化较快，是因为各物理量收敛得较快，与之相对应ρα也较快减小。

从仿真结果曲线可以看出，采用四元数进行变量转换以后，设计的控制输入能够实现水下机器人的点镇定控制，欠驱动AUV的状态变量速度和位移均可以收敛到零。仿真结果证明在3个控制输入的情况下，设计的控制器能够实现三维镇定。

5 结束语

本文讨论了欠驱动AUV的三维镇定控制问题。通过对欠驱动AUV的六自由度空间运动方程和轨迹方程的简化，采用四元数方法进行了模型变换，提出一种具有4个控制输入的连续时变镇定控制律，证明提出的控制律的收敛性，并且进行镇定仿真实验演示。如果在横滚方向的水动力恢复力足够大的情况下，在3个控制输入的情况下AUV可以实现指数镇定。仿真结果表明控制律的有效性，能够在任意初始条件下实现镇定控制。

参考文献:

[1]毕凤阳. 欠驱动自主水下航行器的非线性鲁棒控制策略研究[D]. 哈尔滨：哈尔滨工业大学，2010: 15-18.

BI Fengyang. Research on nonlinear robust control strategies of underactuated autonomous undewater vehicle[D]. Harbin： Harbin Industrial of Technology University, 2010: 15-18.

[2]张铭钧，宋炜胥，褚振忠.自主式水下机器人模糊定性建模方法研究[J]. 哈尔滨工程大学学报，2013， 34(1)： 116-122.

ZHANG Mingjun, SONG Weixu, CHU Zhenzhong. Research on the method of fuzzy qualitative modeling for AUV[J]. Journal of Harbin Engineering University, 2013， 34(1)： 116-122.

[3]PETTERSEN K Y, EGELAND O. Robust control of an underactuated surface vessel with thruster dynamics[C]//Proc 1997 Amer Control Conf. Albuquerque， NM, USA， 1997: 3411-3416.

[4]倪振松,廖启征,魏世民,等. 空间6R机器人位置反解的对偶四元数法[J]. 机械工程学报, 2009， 45(11) : 25-29.

NI Zhensong, LIAO Qizheng, WEI Shimin, et al. Dual four element method for inverse kinematics analysis of spatial 6R manipulator[J]. Journal of Mechanical Engineering, 2009, 45(11) : 25-29.

[5]刘忠,梁晓庚,曹秉刚等. 基于四元数的空间全方位算法研究[J]. 西安交通大学学报, 2006， 40(5) : 618-620.

LIU Zhong, LIANG Xiaogeng, CAO Binggang, et al. Space omnidircetional algorithm study based on quaternion[J]. Journal of Xi′an Jiaotong University, 2006, 40(5) : 618-620.

[6]贾鹤鸣, 程相勤, 张利军,等. 基于自适应Backstepping的AUV的三维航迹跟踪控制[J]. 控制与决策, 2012， 5(27): 652-657.

JIA Heming, CHENG Xiangqin, ZHANG Lijun, et al. Three-dimensional path tracking control for underactuated AUV based on adaptive backstepping[J]. Control and Decision, 2012， 5(27): 652-657.