动态不确定因果图在化工过程故障诊断中的应用

杨佳婧，张勤，朱群雄

(1.北京化工大学 信息科学与技术学院，北京 100029； 2. 北京航空航天大学 计算机学院，北京 100083)

故障诊断主要研究如何对系统中出现的故障进行检测、分离和辨识，即判断故障是否发生，定位故障发生的部位和种类以及确定故障的大小和发生的时间等。在存在多种可能故障的情况下，计算各种故障的概率并根据其大小排序。故障诊断发展至今已经有很多方法，许多学者都对其进行过分类。其中德国的P.M.Frank 教授和美国的Venkatasubramanian 教授的分类方法是比较权威的。Frank教授将故障诊断方法分成基于知识的方法、基于解析模型的方法、基于信号处理的方法三大类[1]。Venkatasubramanian教授将故障诊断方法分为基于模型的定量方法、基于模型的定性方法和基于过程历史的方法三大类[2-4]。基于定量模型的方法要求建立系统的精确解析模型，非常复杂，因而难以实现；基于定性模型的方法利用过程作用的机理和系统元素的关系建立一种定性模型来描述系统，并进行故障诊断，故障推理时有一定的难度；基于数据的方法，要求对大量过程历史数据进行数学分析，挖掘出数据中包含的故障信息，必须利用已知的故障模式，对新出现的故障没有识别能力。每一种故障诊断方法都有各自的优缺点，单一的诊断方法不足以构建实时有效的诊断系统。实际的故障诊断系统通常都采用混合的故障诊断方法。其中，将客观定量数据和主观定性信息进行综合利用是重要的研究方向。基于动态不确定因果图(DUCG)的实时故障诊断方法就是一种定性分析和定量分析相结合的方法，既有由主观经验知识建立的定性模型，也包括客观定量数据的表达，弥补了纯定性方法或纯定量方法的不足。

本文将DUCG理论首次应用于化工过程的实时过程监控和故障诊断，并以国际上广泛采用的TE化工过程模拟器为平台，构建DUCG知识库，建立TE与DUCG之间的在线监测通信接口，进行实时故障诊断测试，取得了理想的结果。

1 动态不确定因果图理论

动态不确定因果图 (Dynamic Uncertain Causality Graph, DUCG) 理论[5-6]是张勤教授提出的一种用于处理不确定因果关系的理论模型。其基本思想是将不确定的因果关系用独立的随机事件并以图形的方式进行表达。由此引入了推理过程中的图形和逻辑化简，首先得到定性推理结果，然后再进行概率数值计算。DUCG的目标是在已知证据和所有假设事件先验概率的情况下，通过推理计算求解当前可能的假设事件及其后验概率。

1.1 DUCG简介

DUCG是一个有向图，图中包含一系列节点和有向弧，其中本文仅涉及多赋值DUCG(M-DUCG)模型，其定义如下：

X节点代表结果变量或事件，分别画为圆形或，其中n标识变量、k标识状态，之间可以用逗号隔开，例如X2,3等。X同时也可以是原因变量或事件，至少有一个输入，可以没有输出，不能是自己的输入和输出

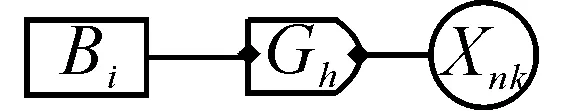
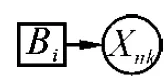
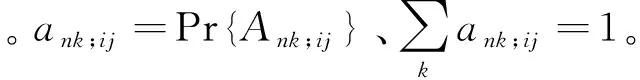
rn;i>0代表父变量Vi与子变量Xn之间的因果关系是否存在及其强度，称为关联度(relationship intensity)。rn;i≠0，否则该因果关系(有向弧)不存在。

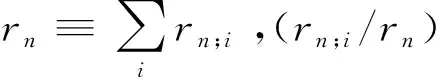
代表条件权重作用事件或事件矩阵，仅在满足给定条件Zn;i的情况下才成立，即当Zn;i满足时，虚线有向弧变成实线有向弧，当Zn;i不满足时，虚线有向弧被删除。Zn;i可以是任何可观测的事件。例如Zn;i=X2,1、Zn;i=B3,0X2,2等等。

1.2 事件展开

文献[5-6]对事件展开给出了详细的定义和解释。设Vi(V∈{B,X,G})是Xn的父变量，则式(1)成立：

(1)

当式(1)中的V为X或G类型节点时，按照上式或G的逻辑表达式继续展开，直到表达式中的所有变量或事件均为{B,A}类型变量或事件和r参数。当有多个X或B类型事件相乘时，需要对它们各自的表达式相乘后进行逻辑吸收或互斥运算，使之成为{B,A}类型事件或变量和r参数的积之和的表达式，然后将大写字母改成小写字母(小写字母代表与大写字母所代表的事件或事件矩阵对应的概率或概率矩阵)，即可计算这些表达式的概率值。逻辑吸收和互斥的运算规则详见参考文献[5-6]。

1.3 DUCG推理计算过程

1)根据接收到的证据信息E将DUCG图中的变量设为相应的状态，以此来初步化简DUCG。

2)文献[5-6]中提出了10条化简规则，根据规则1～10进一步化简已经初步化简的DUCG，规则1～10可按任何顺序反复应用，直到DUCG图不能化简为止。

3)在化简后的DUCG图中收集当前可能的故障假设事件(通常为B类型事件)。

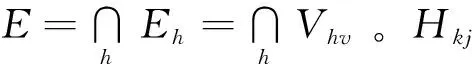
(2)

5)按式(3)计算事件的排序概率：

(3)

2 应用实例

本文首次将DUCG理论应用于化工过程，选取典型的化工过程——TE过程作为研究对象，对其进行实时过程监控和故障诊断。首先，需要对TE过程进行DUCG知识库模型，然后通过接收实时过程信息进行实时过程监控，最后当出现异常信息时，自动启动实时推理计算，确定故障发生的根原因，并计算这些根原因的后验概率，确定各故障原因的概率大小及排序。

2.1 TE过程介绍

TE(Tennessee Eastman)过程是由Downs和Vogel于1993年提出来的一个用来开发、研究和评价过程控制技术和监控方法的典型的化工过程模型[7]。测试过程是基于一个真实工业过程的仿真。TE过程的工艺流程图如图1所示。

TE过程包括5个主要单元：反应器、冷凝器、压缩机、分离器和汽提塔；包含8种成分：A、B、C、D、E、F、G和H。气体成分A、C、D和E以及惰性组分B被喂入反应器，液态产物G和H在反应器中形成，物质F是反应的副产物。反应器中的各种反应为

反应器中的反应产物以蒸汽形式离开反应器，并伴随着部分尚未反应的反应物，通过冷凝器进行冷却，然后送入到气液分离器。从分离器出来的蒸汽通过压缩机再循环送入反应器。为了防止过程中惰性组分B和反应副产品F的积聚，必须排放一部分再进行循环。来自分离器的冷凝成分(流10)被泵送到汽提塔。主要含A、C的流(流4)用于汽提流10中的剩余反应物，这些剩余反应物通过流5与再循环流结合。从汽提塔底部出来的产品G和H被送到下游过程。

TE过程包括41个测量变量和12个操作变量。

2.2 TE过程的DUCG知识库建模

TE过程的DUCG知识库的建造步骤如下：

1)研究确定对象系统即TE过程的{X,B}类型变量，所定义的变量如表1所示。其中，故障发生的根原因被定义为B类型变量，表1中的20个B变量依次对应TE过程中的20个故障；过程中的测量变量和操作变量对应于X类型变量。

续表1

2)对{X,B}类型变量进行状态划分。

3)对B类型变量确定其故障状态概率参数。

4)对每一个X类型变量，建造一个DUCG子模块，具体步骤为：

①选定模块子变量Xn；

②从已定义的{X,B}类型变量中确定Xn的父变量；

③用作用变量或条件作用变量将父变量与子变量Xn相连，其中可能用到逻辑门变量G，其定义见表1中G变量列表；

④对每个作用变量和条件作用变量，确定其关联度rn;i；

⑤由计算机将各子模块连结成完整的DUCG知识库。结果如图2所示。为简单起见，图中X、B、G等字母被省略，因为从其图形形状即可知其为何种类型变量。

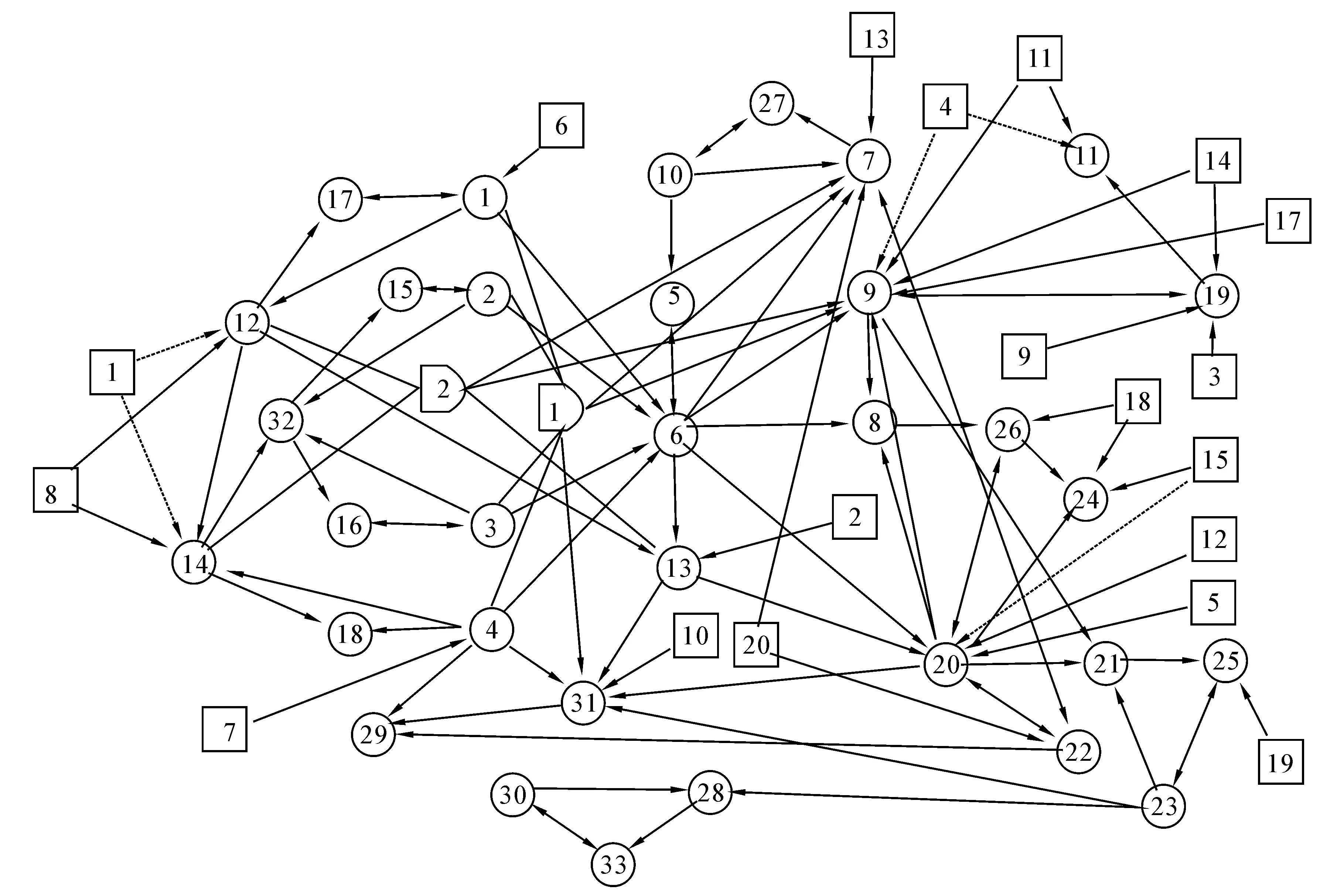
图2 TE过程的DUCG知识库模型Fig.2 The DUCG model of the TE process

2.3 TE过程的实时故障诊断测试

完成TE过程的DUCG知识库建模后，运行TE的MATLAB仿真可产生TE过程的实时数据，用通信模块将DUCG软件系统与之相连，可对TE过程进行实时监控和故障诊断。实验中，在第6小时引入故障。在实时监控中发现有变量处于异常，DUCG软件系统自动启动实时推理诊断，并显示结果。下面选其中2个故障的实验结果进行分析。在诊断结果图中，黄色表示变量值偏高，浅蓝色表示变量值偏低，深蓝色表示变量值极低，粉色表示变量值出现振荡。

2.3.1 故障6

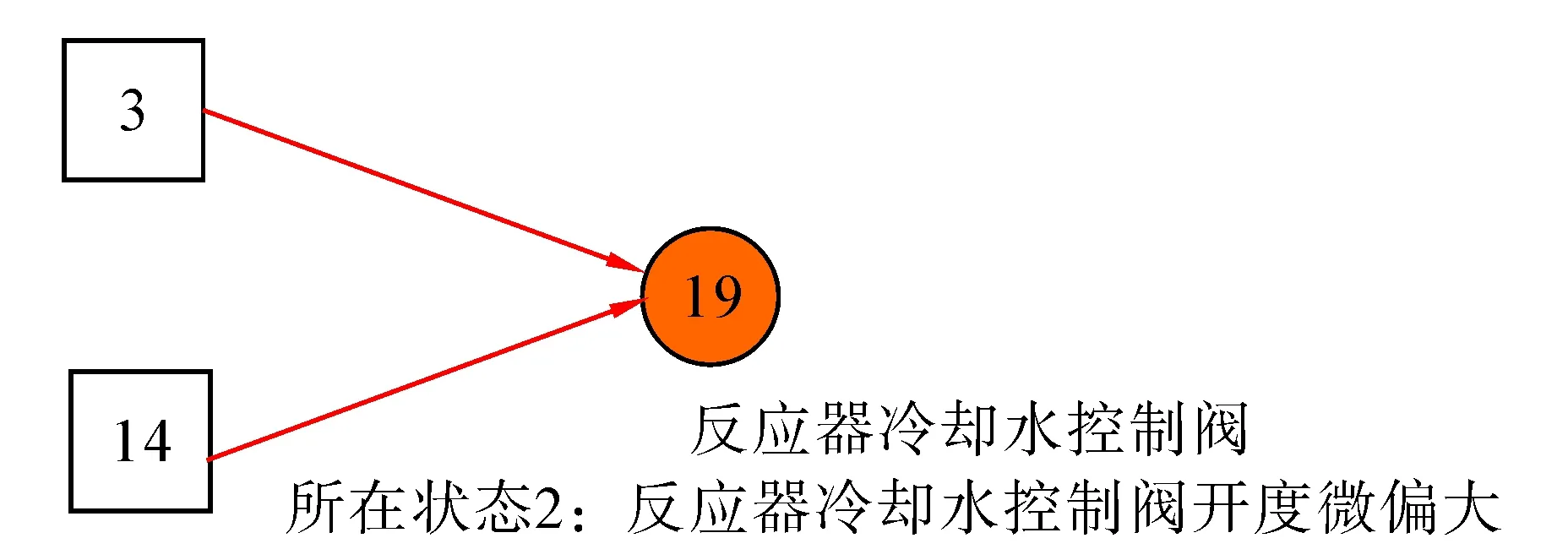
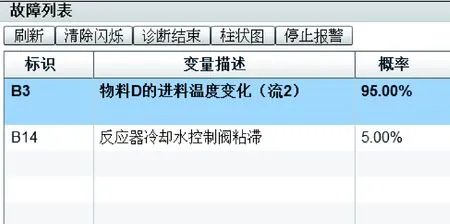
图3所示为引入故障6后，出现型的异常变量的4个时刻(t1

(b)t2时刻诊断结果

(c)t3时刻诊断结果

(d)t4时刻诊断结果图3 故障6的诊断结果Fig.3 The diagnosis results of fault 6

(a) t1时刻诊断结果

2.3.2 故障3

故障3是物料D的进料温度变化(流2)的一个故障。图4所示为引入故障3后，实时推理诊断的结果图。由图4(a)可以看出，变量X19(反应器冷却水控制阀) 出现异常，其开度微偏大，此时推理诊断出的故障原因有2个：B3和B14，即故障3和故障14；再由图4(b)所示的故障列表及计算出的排序概率可以看出，B3的排序概率为95%，排在第一位，B14的排序条件概率仅为5%，因此B3是真正故障原因的概率很大。此故障中，只有t1时刻出现异常，之后未再收到异常信号。

(a) t1时刻故障3诊断结果

(b) t1时刻故障列表及概率图4 t1时刻故障3的诊断结果Fig.4 The diagnosis results of fault 3 at time t1

故障3是TE过程中公认的用其他很多故障诊断方法都很难进行诊断或诊断正确率极低的一个故障。这里用本文提出的基于动态不确定因果图的实时故障诊断方法，诊断出故障3的概率为95%，说明了该方法用于故障诊断的可行性及优越性。TE过程的20个故障的测试结果如表2所示，其中故障16因过程运行数据未出现任何异常，故无故障诊断或故障预报。其余故障的诊断结果良好。

3 结束语

DUCG 模型有3个优点：1)能够直观简洁地表达模块内的各种复杂的不确定因果关系；2)由于引入独立的连接事件或作用事件，且仅表达所关注的因果关系(多数a矩阵为稀疏矩阵)，当获得证据后，可通过删除无关的独立事件而大大化简DUCG图，推理也变得非常容易；3)在建造DUCG 图的过程中，不同的模块可由不同的领域工程师分别独立建造，只要求相同变量的定义保持一致即可。这样，分别独立建造的不同的DUCG模块可以由计算机自动合成为一个完整的DUCG，从而将大型复杂的DUCG 建造和维护问题变得非常简单。

本文将动态不确定因果图理论及其软件系统首次应用于化工过程实时过程监控和故障诊断，以TE过程为具体研究对象进行实验验证，结果良好，尤其对于现有方法难以诊断的故障(故障3、9、15)均有很好的诊断效果，证明了本文采用的基于动态不确定因果图的实时故障诊断方法的有效性，为大型复杂化工过程的实时故障诊断提供了一个新的有效的途径。

参考文献:

[1] FRANK P M. Fault diagnosis in dynamics systems using analytical and knowledge-based redundancy: a survey and some new results[J]. Automatica, 1990, 26(3): 459-474.

[2]VENKATASUBRAMANIAN V, RENGASWAMY R, YIN K, et al. A review of process fault detection and diagnosis part I: quantitative model-based methods[J]. Computers and Chemical Engineering, 2003, 27(3): 293-311.

[3]VENKATASUBRAMANIAN V, RENGASWAMY R, KAVURI S N. A review of process fault detection and diagnosis part II: quantitative model and search strategies[J]. Computers and Chemical Engineering, 2003, 27(3): 313-326.

[4]VENKATASUBRAMANIAN V, RENGASWAMY R, KAVURI S N, et al. A review of process fault detection and diagnosis part III: process history based methods[J]. Computers and Chemical Engineering, 2003, 27(3): 327-346.

[5]ZHANG Qin . Dynamic uncertain causality graph for knowledge representation and reasoning: discrete DAG cases[J]. Journal of Computer Science and Technology, 2012, 27(1.): 1-23.

[6]ZHANG Qin , DONG Chunling , CUI Yan , et al. Dynamic uncertain causality graph for knowledge representation and probabilistic reasoning: statistics base, matrix, and application[J]. IEEE Transactions on Neural Networks and Learning Systems, 2013(99):1-18.

[7]DOWNS J J, VOGEL E F. A plant-wide industrial process control problem[J]. Computers and Chemical Engineering, 1993, 17(3): 245-255