含复折射率缺陷的一维线性函数光子晶体的电场特性

李 宏，孟祥东，吴向尧，马 季，刘晓静，张斯淇，王 婧

（吉林师范大学物理学院，吉林四平 136000）

含复折射率缺陷的一维线性函数光子晶体的电场特性

李 宏，孟祥东，吴向尧，马 季，刘晓静，张斯淇，王 婧

（吉林师范大学物理学院，吉林四平 136000）

用传输矩阵法计算光在掺杂金属缺陷的线性函数光子晶体中的电场分布，考察缺陷层位置、层数以及光子晶体半周期数对电场分布的影响，并与不含缺陷的结构进行比较.结果表明，有缺陷光子晶体的电场分布强度明显增强.

函数光子晶体；传输矩阵；缺陷层；电场分布

介电常数和真空磁导率分别为ε0＝8.854×10－12和μ0＝12.566×10－7；θ0i为入射角.

缺陷层的复折射率nd＝nd（0）－i k，其中nd（0）和k分别为缺陷层复折射率的实部和虚部，缺陷层传输矩阵为

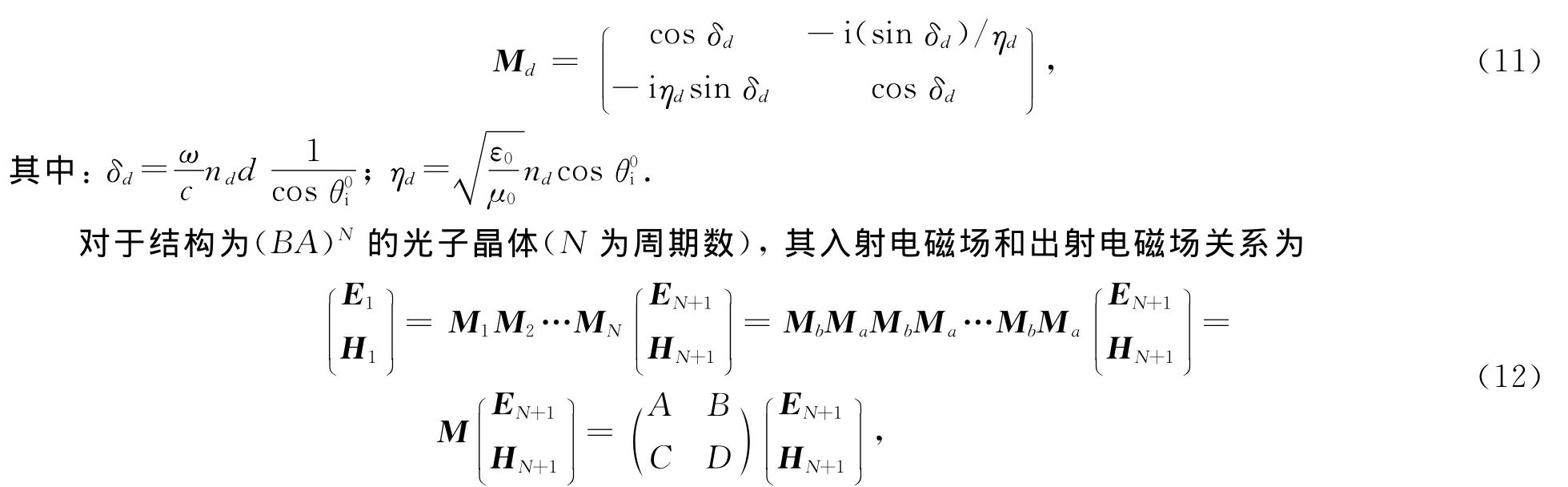
其中M＝MbMaMbMa…MbMa，方程（12）即为以角θ0i入射的光在一维线性函数光子晶体中的传输矩阵.

光在一维线性函数光子晶体中传播的透射率和反射率［10－11］分别为：

透射系数：

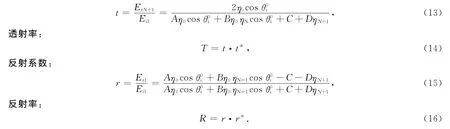
由一维函数光子晶体的传输矩阵可得光在光子晶体中的电场分布为

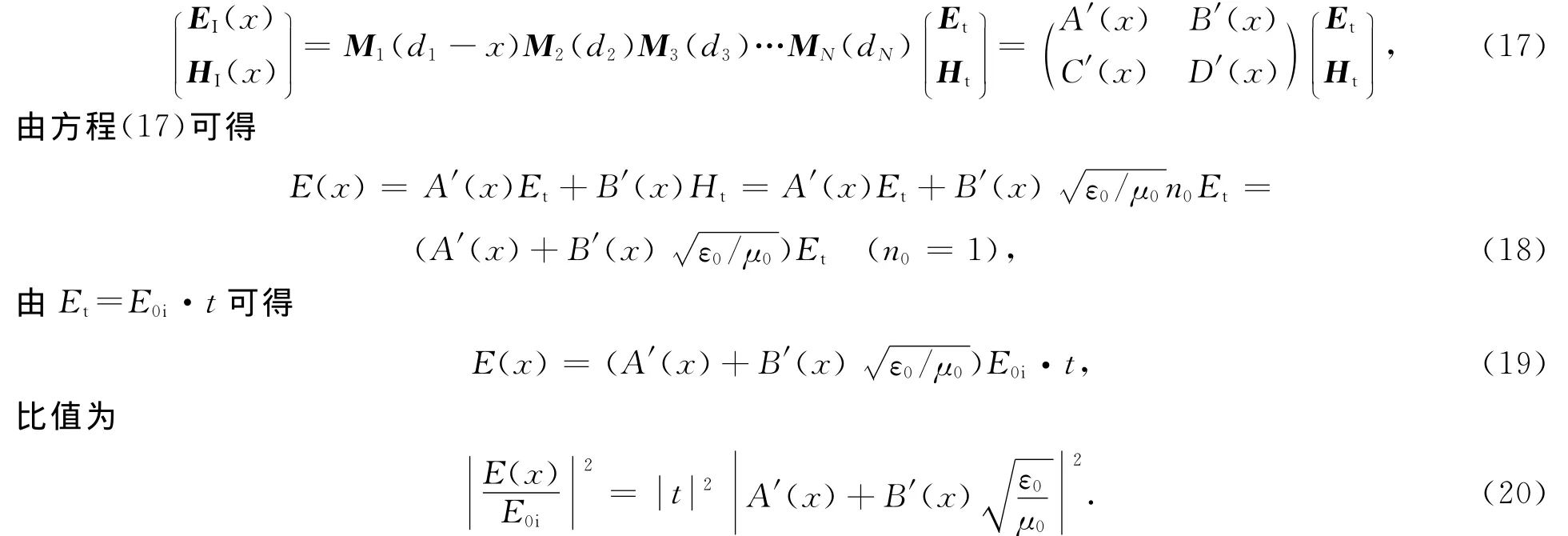
方程（20）即为一维函数光子晶体的电场分布公式.

2 数值分析

折射率为空间坐标线性函数的光子晶体，折射率分布函数为：

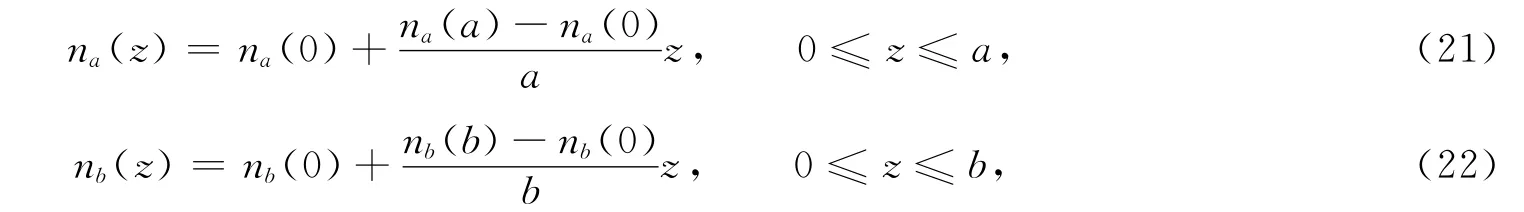
其折射率随位置变化的关系曲线如图1所示.

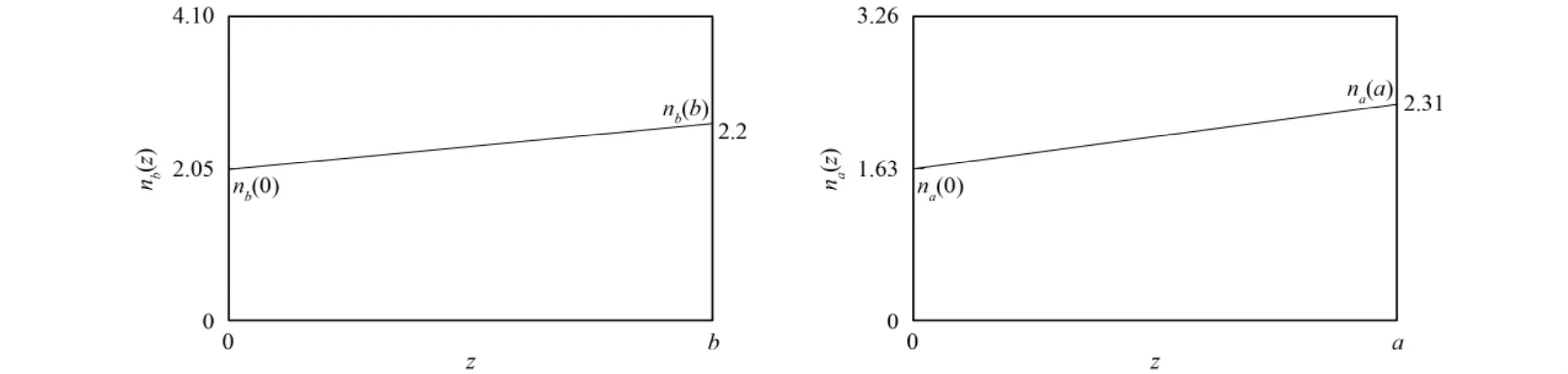
图1 线性函数光子晶体折射率随位置变化的关系曲线Fig.1 Refractive index of linear function photonic crystal change with position

计算中的各参数分别取为：nb（0）＝2.05；nb（b）＝2.2；na（0）＝1.63；na（a）＝2.31；入射角θ0i＝0；中心频率ω0＝1.216×1015Hz；λ0＝2πc／ω0；光学厚度naa＝nbb＝λ0／4，其中a和b分别为介质层A和B的厚度，周期数N＝16，即结构为（BA）16；缺陷层的折射率为复数，即nd＝nd（0）－i k，分别取nd（0）＝2.1，k＝0.05，nd（0）d＝λ0／4，d为缺陷层D的厚度.

结构为（BA）16和（BA）8D（BA）8的一维线性函数光子晶体的场强分布曲线如图2所示，其中横轴为光在函数光子晶体中的传播位置，纵轴为该位置处场强与入射场强比值的模方.由图2可见，光子晶体中插入复折射率缺陷层的电场分布强度明显高于无缺陷时的电场分布强度，表明光子晶体中插入缺陷可改变整体的电场分布，输出的电场强度更大.

当缺陷层分别插在第8，10，12周期处时，即结构分别为（BA）8D（BA）8，（BA）10D（BA）6和（BA）12D（BA）4时的线性函数光子晶体的场强分布曲线如图3所示，其中横轴为光在函数光子晶体中的传播位置，纵轴为该位置处场强与入射场强比值的模方.由图3可见，随着缺陷层向后移动，场强分布呈减小的趋势.

当缺陷层层数分别为1，3，5时，即结构分别为（BA）8D（BA）8，（BA）10D3（BA）8，（BA）8D5（BA）8的线性函数光子晶体的场强分布曲线如图4所示，其中横轴为光在函数光子晶体中的传播位置，纵轴为该位置处场强与入射场强比值的模方.由图4可见，当缺陷层层数呈奇数倍增加时，电场分布强度明显增强.

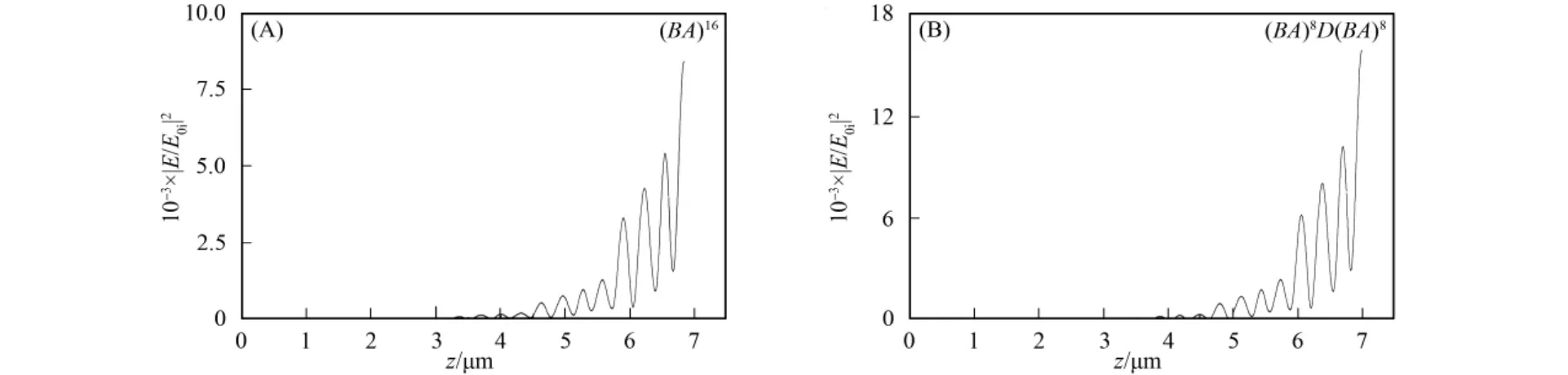
图2 结构为（BA）16和（BA）8 D（BA）8的函数光子晶体的场强分布曲线Fig.2 Electric field distribution of the function photonic crystals with the structure are（BA）16 and（BA）8 D（BA）8

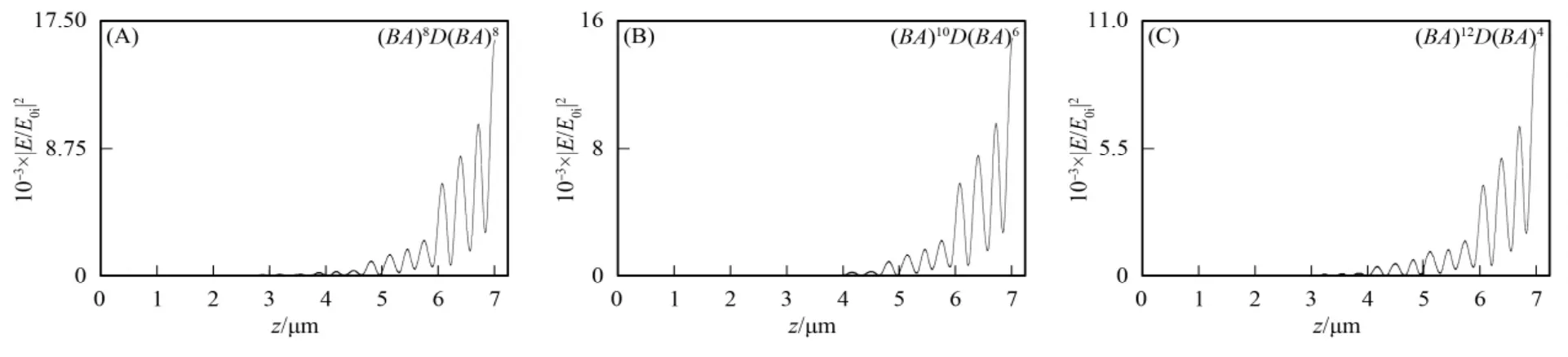
图3 缺陷层在不同位置时函数光子晶体的场强分布曲线Fig.3 Electric field distribution of the function photonic crystals with defect layer at different positions

图4 函数光子晶体中不同缺陷层层数的场强分布曲线Fig.4 Electric field distribution of the function photonic crystals with different numbers of defect layers

当函数光子晶体的结构为（BA）ND（BA）N（N为半周期数）时，半周期数对一维线性函数光子晶体的影响如图5所示，图5（A）～（C）中的半周期数N分别为8，6，4.由图5可见，当半周期数N减小时，其场强分布锐减，这是由于电磁波在非均匀介质中传播吸收了能量，使电场强度增加所致［13］.因此由非均匀介质构成的函数光子晶体，其电场强度在每个周期均会增加.

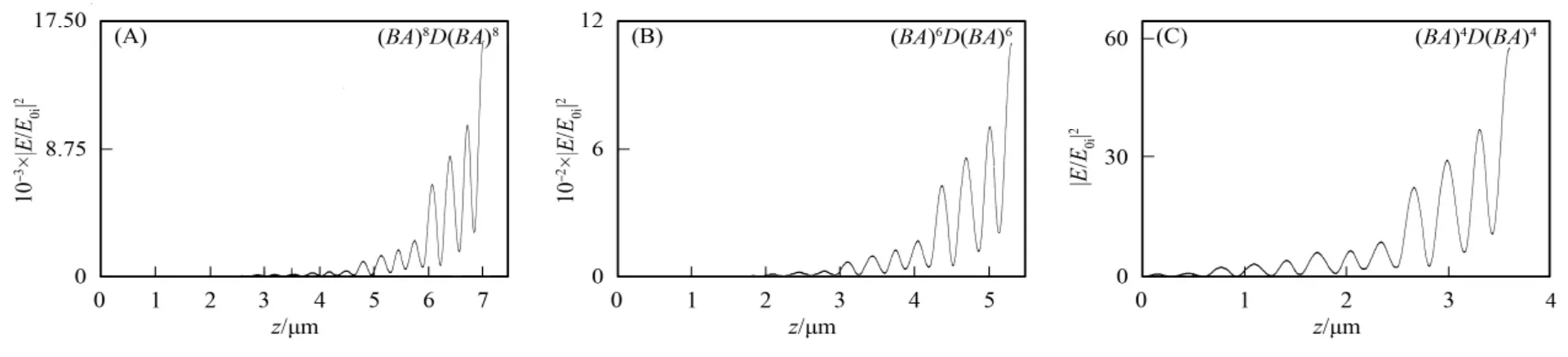
图5 函数光子晶体中不同半周期数N的场强分布曲线Fig.5 Electric field distribution of the function photonic crystals with different half period numbers N

综上，本文用传输矩阵法计算了光在掺杂金属缺陷的一维线性函数光子晶体中的电场分布，并考察了缺陷层位置、层数和半周期数对电场分布的影响，可得如下结论：

1）光子晶体中插入缺陷层后的电场分布强度明显高于无缺陷时的电场分布强度；

2）随着缺陷层向后移动，电场分布强度变弱；

3）当线性函数光子晶体中的缺陷层层数奇数倍增加时，电场分布强度增强；

4）当光子晶体中的半周期数减小时，电场分布强度锐减.

［1］ John S.Strong Localization of Photons in Certain Disordered Dielectric Superlattices［J］.Phys Rev Lett，1987，58（23）：2486－2489.

［2］ Yablonovitch E.Inhibited Spontaneous Emission in Solid－State Physics and Electronics［J］.Phys Rev Lett，1987，58（20）：2059－2062.

［3］ Belov P A.Backward Wave and Negative Refraction in Uniaxial Dielectrics with Negative Dielectric Permittivity along the Anisotropy Axis［J］.Microw Opt Tech Lett，2003，37（4）：259－263.

［4］ Prior J，Vega I，de，Chin A W，et al.Quantum Dynamics in Photonic Crystals［J］.Phys Rev A，2013，87（1）：013428.

［5］ Fan S，Villenenve P R，Joanhopoulos J D，et al.High Extraction Efficiency of Spontaneous Emission from Slabs of Photonic Crystals［J］.Phys Rev Lett，1996，78（17）：3294－3297.

［6］ Yakoyama H，Nishi K，Anan T，et al.Controlling Spontaneous Emission and Threshold－Less Laser Oscillation with Optical Microcavities［J］.Optical and Quantum Electronics，1992，24（2）：S245－S272.

［7］ 李文胜，张琴，黄海铭，等.含复折射率介质一维准周期光子晶体的透射特性［J］.量子光学学报，2013，19（2）：171－176.（LI Wensheng，ZHANG Qin，HUANG Haiming，et al.Transmission Characteristics of 1－D Quansiperiodic Photonic Crystal with Complex Refractive Index Medium［J］.Acta Sinica Quantum Optica，2013，19（2）：171－176.）

［8］ 杨光杰，孔凡敏，梅良模.金属光子晶体禁带研究［J］.光子学报，2007，36（10）：1821－1823.（YANG Guangjie，KONG Fanmin，MEI Liangmo.Band Gaps of Photonic Crystal Composed of Metallic Cylinders［J］.Acta Photonica Sinica，2007，36（10）：1821－1823.）

［9］ 王光怀，王清才，吴向尧，等.一维函数光子晶体的研究 ［J］.物理学报，2012，61（13）：134208.（WANG Guanghuai，WANG Qingcai，WU Xiangyao，et al.Research on One－Dimensional Function Photonic Crystals［J］.Acta Physica Sinica，2012，61（13）：134208.）

［10］ WU Xiangyao，ZHANG Bojun，YANG Jinghai，et al.The Characteristic of Light Transmission of Function Photonic Crystals［J］.Physica E，2012，44（7／8）：1223－1229.

［11］ WU Xiangyao，ZHANG Bojun，YANG Jinghai，et al.Transmission Character of General Function Photonic Crystals［J］.Physica E，2012，45：166－172.

［12］ WU Xiangyao，ZHANG Bojun，LIU Xiaojing，et al.Light Field Distribution of General Function Photonic Crystals［J］.Physica E，2012，46：133－138.

［13］ 张斯淇，吴向尧，刘晓静，等.新型线性函数光子晶体的光子二极管［J］.吉林大学学报：理学版，2013，51（5）：912－918.（ZHANG Siqi，WU Xiangyao，LIU Xiaojing，et al.Photon Diode of Linear Function Photonic Crystals［J］.Journal of Jilin University：Science Edition，2013，51（5）：912－918.）

（责任编辑：王 健）

Election Field Distribution of 1－D Linear Function Photonic Crystal with Complex Refractive Index Medium

LI Hong，MENG Xiangdong，WU Xiangyao，MA Ji，LIU Xiaojing，ZHANG Siqi，WANG Jing
（College of Physics，Jilin Normal University，Siping136000，Jilin Province，China）

The light propagation characteristic in one－dimensional function photonic crystal with metal defect was studied by transfer matrix，and compared with that of the function photonic crystal without defect layer，showing electric field intensity enhance obviously.We researched the effects of the position and the number of defect layers on electric field distribution.Then we studied the electric field distribution via changing the half period numbers.

function photonic crystals；transfer matrix；defect layer；electric field distribution

O436

A

1671－5489（2014）04－0811－05

光子晶体可通过改变不同折射率材料的堆积方式实现对光传播的控制［1－2］，由于其具有类似半导体能带的禁带，因此光子晶体在光学物理、凝聚态物理、电磁波和信息技术等领域应用广泛［3－8］.文献［9－12］提出了一种新型的函数光子晶体，即折射率是空间位置的任意函数，得到一些与常规光子晶体不同的特性.本文在此基础上，通过在函数光子晶体中插入金属缺陷层，即缺陷层折射率为复数，考察其缺陷层的位置、层数以及不同半周期数对电场分布的影响.

1 原 理

10.13413／j.cnki.jdxblxb.2014.04.35

2013－12－17.

李 宏（1989—），男，汉族，硕士研究生，从事理论物理的研究，E－mail：993387662＠qq.com.通信作者：吴向尧（1965—），男，汉族，博士，教授，从事理论物理的研究，E－mail：wuxy2066＠163.com.

国家自然科学基金（批准号：61275047）和吉林省科技厅项目（批准号：20130101031JC）.