鄂尔多斯盆地上三叠统延长组机械压实作用与砂岩致密过程及对致密化影响程度

刘明洁,刘震,刘静静,蔡长娥,张胜斌

中国石油大学油气资源与探测国家重点实验室,北京,102249

内容提要: 近年来,随着致密砂岩油气藏研究的不断深入,亟需明确致密砂岩储层致密化机理,从而更好地利于致密砂岩油气藏的勘探与开发。机械压实作用通常被理解为中浅层砂岩所经历的主要成岩作用,而深层的机械压实作用长期以来被人们所忽视。为探讨机械压实作用在砂岩致密过程中的作用及对致密化的影响程度,本次研究以鄂尔多斯盆地上三叠统延长组致密砂岩为例,通过井孔浅层与深层孔隙度变化趋势分析、镜下岩石结构的证据和砂岩压实模拟实验3个方面对延长组致密砂岩储层机械压实作用特征进行了分析。研究发现砂岩在深层与浅层压实减孔趋势一致或平行；随着上覆压力的增加,砂岩一直表现为减孔效应且机械压实作用强度随埋深的增加而变大；薄片特征显示延长组致密砂岩机械压实作用存在分级特征,不同级别的压实强度对应一定的镜下压实特征,通过统计薄片数据发现样品都处于压实作用与胶结作用对孔隙度影响评价图(Houseknecht图版)的左下区域。结果表明砂岩在埋藏致密化过程中自始至终存在机械压实作用,并且机械压实作用是导致砂岩致密减孔最重要的原因,远远超过胶结作用产生的减孔效应。由于砂岩孔隙度演化不仅与埋深有关,同样受到地质时间的影响,本次研究通过数学推导建立了砂岩孔隙度时间埋深双元函数模型,进而通过孔隙度双元函数可以对压实减孔进行定量分析,表征机械压实作用对砂岩致密化过程的影响程度。

随着成岩作用和成岩动力学研究的不断深入 (Johnson,1920；Carothers and Kharaka,1978；Surdam et al.,1984,1989；Ehrenberg,1990,1993；鲜本忠等,2004；李忠等,2006；刘宝珺,2009；Bjørlykke and Jahren,2012),储层成岩作用对储层原始物性的改造决定了储层的储集性能,而储集性能又是油气成藏的关键因素,因而在油气勘探领域储层物性变化过程逐渐为众多学者所重视(肖丽华等,2003；张雪芬等,2013)。目前对砂岩储层成岩作用的研究大多集中在定性的描述和分析阶段,勘探开发中过多关注储层特征的表征(白玉宝,1996；罗静兰等,2001；邱隆伟等,2001；张鼐等,2008；Gier et al., 2008; 王瑞飞等,2008, 2009；柳益群等,2009； Khidir and Catuneanu, 2010)。依据动态成藏观点,现今储层物性并不能代表成藏期油气充注时储层的储集性能,因此只有定量分析砂岩储层所经历的成岩作用过程,明确不同成岩作用对砂岩成岩过程的影响程度,才能有助于开展成藏条件分析,并更好地指导油气勘探。与其他成岩作用相比,压实作用主要表现为使砂岩孔隙度变小,是指沉积物沉积后在其上覆水体或沉积层的重荷下,或在构造形变应力的作用下,发生水分排出、孔隙度降低、体积缩小的作用(Makowitz et al., 2006)。

对于砂岩压实作用的研究,前人除了对砂岩储层压实作用特征进行表征外,还对压实作用其他方面做了大量的工作。李忠等(2009)通过对塔里木盆地库车坳陷的研究,分析压实作用与构造应变的关系,提出了砂岩储层改造的构造样式,探讨了构造应变与砂岩成岩的构造非均质性。Souque等(2011)研究阿塞拜疆Apsheron半岛构造作用对砂岩机械压实的控制,认为构造作用一方面促进压实使砂岩致密物性变差,一方面又因砂岩致密化易产生裂缝从而改善砂岩物性。Gutierrez 和 Wangen(2005)通过对沉积盆地压实作用和超压作用模型的研究,指出超压能导致欠压实和不均衡压实,表现出高孔隙度特征。Houseknecht(1987)通过砂岩压实作用和胶结作用对砂岩孔隙度降低相对重要性的对比,指出在决定最终孔隙度方面压实作用比胶结作用重要得多,强调在进行储层砂岩分析和埋藏成岩作用模拟时,必须结合对压实作用的评估。Lander 和 Walderhaug(1999)、刘国勇等(2006)及操应长等(2011)通过模拟实验对砂岩压实作用进行研究,再现了压实作用过程,以此定性分析了压实作用对砂岩储层物性的影响。

可以看出,前人研究主要集中于压实作用定性的描述、分析、模拟及趋势性预测,而针对机械压实作用在砂岩致密化过程中所起的作用及影响程度的定量研究工作相对比较少。笔者近年来在致密砂岩油气藏的研究过程中发现实际资料与深层压实终止论不符,在深部的致密砂岩中仍可见砂岩压实现象。通过前人大量研究成果的调研,发现深部砂岩储层仍存在机械压实证据(Milliken, 1994;Fisher et al., 1999; Chuhan et al., 2002; Makowitz and Milliken, 2002)。

本文以砂岩孔隙度演化趋势、砂岩镜下结构和砂岩压实模拟实验为切入点,针对机械压实作用在砂岩致密化过程中所起的作用及影响程度进行分析,进而利用数学模型推导对机械压实作用进行定量化研究,通过砂岩储层孔隙度演化来表征机械压实作用在成岩过程中的影响程度。

1 井孔砂岩孔隙度演化趋势

孔隙度—深度趋势可以提供机械压实作用发生的证据(Ramm,1992;Giles,1997)。整体上,井孔砂岩孔隙度随埋深增大而减小,符合Athy(1930)模型。在中浅层由于不考虑砂岩孔隙度增孔效应,在对数坐标下的孔隙度与直线坐标下的埋藏深度交会图上,会表现出孔隙度随埋深增加正比例减小的趋势。本文选取鄂尔多斯盆地典型井(图1),分析半对数坐标下砂岩孔隙度与埋深关系,对比深层与中浅层砂岩孔隙度演化趋势,发现两个现象,即一是深层砂岩压实趋势与中浅层砂岩压实趋势完全一致,二是深层砂岩压实减孔趋势与中浅层砂岩压实趋势平行。

1.1 深层砂岩压实趋势与中浅层压实趋势完全一致

长期以来,很多人认为机械压实作用只发生在中浅层,到了深层机械压实作用就消失了(Ramm,1992；Ramm and Bjørlykke,1994; Giles,1997, Bernaud et al., 2006; Mondol et al., 2007;Agersborg et al., 2011)。但是实际上在砂岩孔隙度与埋深图上可以看到深层仍然存在减孔现象,而且深层减孔趋势与中浅层减孔压实趋势重合。以鄂尔多斯盆地南部镇泾地区HH38井为例,分析砂岩孔隙度深度关系(图2a)可以发现,在次生孔隙发育带之上,砂岩孔隙度在半对数坐标下随埋深增加呈线性递减趋势,进入次生孔隙发育带后,砂岩由于溶蚀增孔效应孔隙度变大,孔隙度偏离正常压实趋势,越过次生孔隙发育带后,孔隙度仍保持随埋深增加而线性减小的趋势,且与次生孔隙发育带之上的正常压实趋势完全一致。

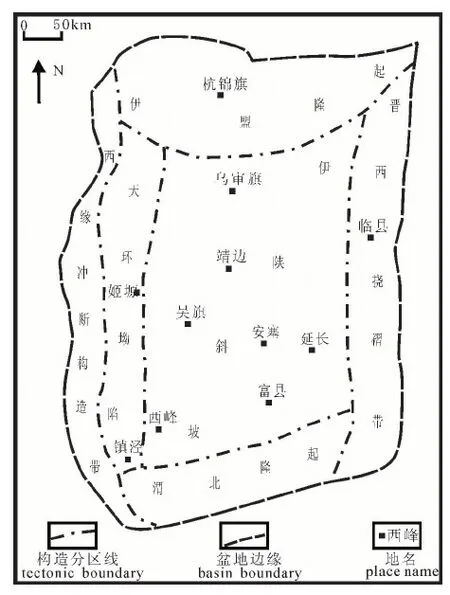
图1 鄂尔多斯盆地构造单元图Fig. 1 The structure unites of Ordos Basin

1.2 深层砂岩压实减孔趋势与中浅层压实减孔趋势平行

深层砂岩压实减孔趋势还可表现出另外一种现象,即表现为深层砂岩减孔趋势与中浅层压实减孔趋势平行的特征。分析鄂尔多斯盆地姬塬地区Y71井砂岩孔隙度深度关系图(图2b)、准噶尔盆地MS1井压实曲线(图3a)和准噶尔盆地腹部侏罗系砂岩埋深与孔隙度关系(图3b)表明：在次生孔隙发育带之上,半对数坐标下中浅层砂岩孔隙度随埋深增加呈线性递减趋势,进入次生孔隙发育带后,砂岩由于溶蚀增孔效应孔隙度变大而偏离正常压实趋势,此后随着埋深的增加,在溶蚀增孔的基础上孔隙度始终保持随埋深增加而线性减小趋势,呈现出深层砂岩相对于中浅层砂岩压实趋势整体平行偏移的特点。

从上述两种情况表明,在砂岩沉积后的埋藏过程中始终存在着机械压实作用。机械压实作用不仅在中浅层中存在,在长期以来被人们所忽视的深层依然存在,为致密砂岩储层的形成提供了有利条件。

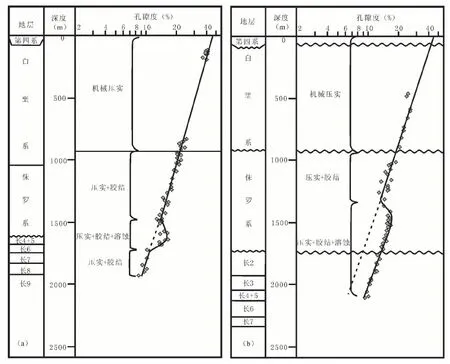
图2 鄂尔多斯盆地砂岩孔隙度深度关系图Fig. 2 Relationship between depth and porosity of sandstone in Ordos Basin (a)HH38井；(b)Y71井 (a)well HH38; (b) well Y71

2 致密砂岩储层镜下机械压实作用特征

致密砂岩储层镜下矿物颗粒表现出的特征能反映砂岩所经受的机械压实作用。本次研究通过镜下薄片的观察,分析了鄂尔多斯盆地延长组致密砂岩的机械压实作用特征,并通过对压实作用与胶结作用对孔隙度影响程度评价,明确了砂岩储层致密化的主控因素。

图3 准噶尔盆地浅层砂岩与深层砂岩压实趋势关系Fig. 3 Relationship of sandstone compaction trend between shallow layer and deep zone in Jungar Basin (a)MS1井压实曲线；(b)准噶尔盆地腹部侏罗系砂岩埋深与孔隙度关系图(据金振奎等,2011,有修改) (a)compaction curve of well MS1; (b) Relationship between burial depth and porosity of Jurassic sandstone in central Jungar Basin (from Jin Zhenkui, 2011, modified)

2.1 致密砂岩机械压实作用定量分级

本次研究从埋藏深度、颗粒接触类型比例、塑性颗粒变形角度和长石颗粒变形破裂程度等方面对延长组致密砂岩储层机械压实作用强度进行了定量分级,将机械压实作用划分为弱压实(Ⅰ级)、中弱压实(Ⅱ级)和中等压实(Ⅲ级)三类(表1),特征如下。

(1)弱压实(Ⅰ级)：延长组弱压实(Ⅰ级)主要变现为埋深<1200m,颗粒点接触比例>75%,线接触比例<25%,无凹凸接触(图4a),塑性云母颗粒变形角度<30°(图4b),无长石颗粒变形破裂现象。

表1 鄂尔多斯盆地延长组致密砂岩机械压实作用强度定量分级表Table 1 The quantitative table of the mechanical compaction grading to the tight sandstone of Yanchang Formation in Ordos Basin

(2)中弱压实(Ⅱ级)：延长组弱压实(Ⅱ级)主要变现为埋深1200～1700m,颗粒点接触比例50%～75%,线接触比例25%～50%,无凹凸接触(图4c),塑性云母颗粒变形角度30°～45°(图4d),可见长石颗粒变形为主(图4e)。

(3)中等压实(Ⅲ级)：延长组弱压实(Ⅲ级)主要变现为埋深1700～2200m,点接触比例<25%,线接触比例50%～75%,凹凸接触比例<25%(图4f),塑性云母颗粒变形角度>45°(图4g),可见长石颗粒破裂为主(图4h)。

通过对延长组致密砂岩储层机械压实作用强度定量研究可以发现,随埋深的增加机械压实作用强度变大。由于机械压实作用是不可逆的,不存在深部成岩之后抬升浅保存可能；同时一定的埋深对应着特定的机械压实作用强度及特征,排除了浅部成岩深部保存的可能。因而研究表明机械压实作用一直存在于致密砂岩储层成岩过程中。

2.2 砂岩储层致密化的主控因素

压实作用和胶结作用是导致砂岩减孔最主要的原因 (Wilson and McBride, 1988; Lundegard,1992; Ehrenberg , 1995; 寿建峰等,2006),但砂岩储层致密化的主控因素一直认识不清(Houseknecht, 1987 ; Pate,1989; Ehrenberg,1989)。本次研究以鄂尔多斯延长组致密砂岩为例利用Houseknecht(1987)图版,通过镜下薄片统计,定量评估压实作用和胶结作用对孔隙度影响,绘制了压实作用和胶结作用相对作用大小图版(图5)。从图中可以看出,样品数据主要分布在图版左下区域,表明砂岩储层在致密化过程中主要受压实作用控制。

3 致密砂岩压实作用实验模拟结果

本文利用双轴承压压实作用模拟实验,在测定不同压力条件(上覆地层压力和侧向地层压力)对应的砂岩孔隙度数据,通过分析有效应力和砂岩孔隙度之间的关系,来证明机械压实作用一直存在于砂岩储层致密化过程中。

3.1 实验原理、装置及方法

3.1.1 实验基本原理

双轴承压实验就是给砂岩样品施加一个轴压和一个围压来分别模拟侧向地层压力和上覆地层压力,其中围压是由人工控制的,以5MPa的增量逐渐增加,轴压则是通过地下岩层的平衡关系来确定。在此过程中,利用超声波测量仪直接测定与围压和轴压相对应的砂岩孔隙度值。

3.1.2实验装置

砂岩样品双轴承压实验装置包括围压监测设备、轴压监测设备、流压监测设备、岩心夹持器、以及超声波测量仪等。

本次实验最大围压Pw可达40MPa,轴压由关系式Pz=Pw·γ/(1-γ)计算得到,γ是动态泊松比,由纵横波速度来确定。样品在夹持器中的受力如图6所示。

3.1.3实验方法

本次实验通过模拟不同埋深条件下的上覆压力和侧向地层压力,测算与上覆压力对应的砂岩岩芯样品的孔隙度值,进而通过换算得到有效应力与砂岩孔隙度的关系。随着有效应力的变化,当砂岩孔隙度逐渐减小至10%以下成为致密砂岩时,分析这一过程中孔隙度与有效应力之间的关系,进而明确机械压实作用是否影响了砂岩致密化过程。

图4 鄂尔多斯盆地上三叠统延长组致密砂岩机械压实作用镜下特征Fig. 4 The tight sandstones characteristics of the microscope in Upper Triassic Yanchang Formation, Ordos Basin (a) 应1井,1163m,×5,单偏光；(b)塞129井,1142m,×10,单偏光；(c)塞193井,1539m,×10,单偏光；(d)镰34井,1356m,×20,正交光；(e)塞404井,1280m,×20,正交光；(f)西33井,1996.5m,×5,单偏光；(g)西128井,1987.55m,×10,单偏光；(h)西180井,2112.1m,×20,正交光 (a) well Ying1,1163m, ×5, single polar; (b) well Sai129, 1142m,×10, single polar; (c) well Sai193, 1539m,×10, single polar; (d)well Lian34, 1356m,×20, Orthogonal light; (e) well Sai404, 1280m,×20, Orthogonal light; (f) well Xi33, 1996.5m,×5, single polar; (g) well Xi128, 1987.55m,×10, single polar; (h) well Xi180, 2112.1m,×20, Orthogonal light

图5 鄂尔多斯盆地上三叠统延长组压实作用与胶结作用对孔隙度影响评价图Fig. 5 The effect evaluation map of the compaction and the cementation to the Upper Triassic Yanchang Formation in Ordos Basin (a) 西峰地区延长组；(b) 安塞地区延长组 (a) Yanchang Formation of Xifeng Area; (b) Yanchang Formation of Ansai Area

图6 双轴承压压实作用模拟实验砂岩样品受力示意图Fig. 6 Scheme of force analysis to sandstone sample during simulation experiment

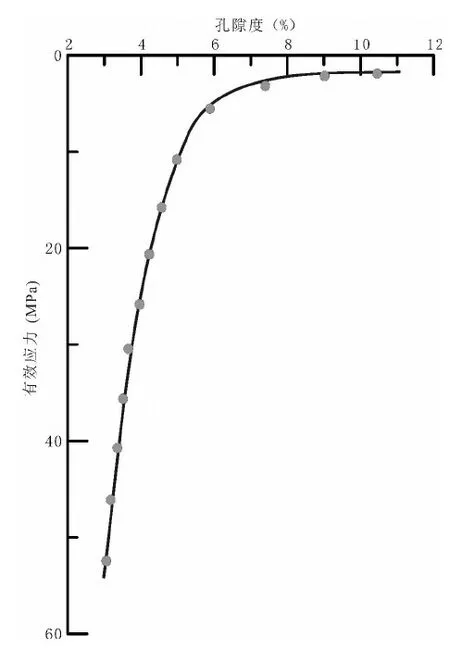
图7 鄂尔多斯盆地上三叠统延长组X17井 孔隙度与有效压力关系图Fig. 7 The relationship map between porosity and effective stress of the Upper Triassic Yanchang Formation in Ordos Basin

3.2 实验数据分析

本文以鄂尔多斯盆地延长组为例,对长8段砂岩样品进行压实作用模拟。

由于实验中的围压代表上覆地层负荷压力,利用Terzaghi(1925)模型计算有效应力,进而分析有效应力与孔隙度关系(图7)可知,孔隙度与有效应力呈现出良好的幂函数关系,表明随着有效应力增大,砂岩孔隙度会逐渐变小,并且当砂岩孔隙度减小到10%以下成为致密砂岩后,随着有效压力的增加,孔隙度继续保持减小的趋势。这一现象与常见的覆压实验中,当覆压逐渐超过现今埋深的等效压力后,孔隙度仍然持续减小的趋势一致(图8)。

通过压实模拟实验表明：随着砂岩的埋深,上覆地层负荷的增加,机械压实作用一直会对砂岩孔隙度表现出减小的效应,一直存在于砂岩储层致密化过程中。

4 压实作用阶段砂岩孔隙度演化定量模型分析

尽管Athy(1930)提出了正常压实条件下的泥岩孔隙度与埋深之间存在指数关系,这一模型同样被广泛地运用到砂岩研究中,而众多研究者尝试通过薄片观察统计建立压实作用的减孔模型(Stephenson et al., 1992; Ehrenberg et al., 1995; Paxton et al., 2002)。但随着研究的不断深入,越来越多的学者认为砂岩孔隙度不仅与埋深有关,同样受到地质时间的影响(Maxwell,1964; Schere, 1987; Hayes, 1991; Ehrenberg et al., 2009)。本文试图根据数学推导,证实埋深和埋藏时间对地层孔隙度有很大的影响,提出了压实作用过程中地层孔隙度受埋深和埋藏时间双重作用控制的数学模型。

由岩石力学基本理论可知,岩体是由岩块及各岩块之间的弱面和不连续面构成,而岩块是连续的岩石块体,是组成岩体的基本实体。孔隙结构型岩块受载时表现出复杂的力学性质：当时间延长时,由于岩块中原子和离子的热运动,弹性变形会消失,进而转变为塑性变形,应力随之减小。但由于岩块中存在内摩擦,加载后不能立即达到最终的变形,而是随时间的延长而逐渐增加,即蠕变效应。

显然,孔隙性地层在埋藏压实过程中所发生的变形既不是纯弹性变形也不是纯塑性变形, 而是存在内摩擦作用的粘弹塑性变形。既然孔隙性地层的受力变形过程是粘弹塑性变形过程,那么其应力应变关系就不能用简单的胡克定律(完全弹性变形模型)来表示,也不能用完全塑性变形模型来表示,而需要用粘弹塑性应力应变模型来表达。笔者认为,粘弹塑性应力应变模型是最适用于砂泥岩地层压实变形的应力应变模型,其中Bingham模型更适合于表达砂泥岩地层的受力变形过程。Bingham粘弹塑性应力应变模型的形式如下:

(1)

ε≈∆φ

(2)

另有,地层垂向受力与地层平均密度成正比,即：

σ=ρsgZ

(3)

其中：ρs为地层平均密度,g/cm3,Z为地层埋深,m。因此,(1)式变为:

(4)

从(4)式可以看出,地层孔隙度的变化率与埋深和埋藏速率有关。因此,可以认为地层孔隙度的变化必然与埋藏时间有关。

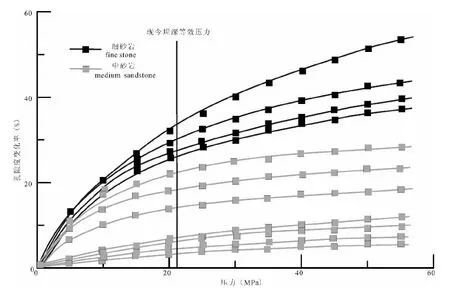
图8 鄂尔多斯盆地镇泾地区长8砂岩孔隙度变化率与覆压关系图Fig. 8 The relationship map between changing rate of sandstone porosity and overburden pressure within the 8th Member, Yanchang Formation,Zhenjing aera,Ordos basin

对于一个埋藏速率为k的等速埋藏过程,对(4)式两边求积分,将得到下式

(5)

φ0为初始孔隙度,%。显然,在一个等速埋藏阶段,地下地层的孔隙度不但与阶段最终埋深Z有关,而且与经历的阶段总时间t有关,另外与该变形阶段的初始孔隙度φ0也有关系。从 (5)式也可以看出,对于一定的岩层和给定的阶段,A、B、C和φ0这 4项参数可以视为常量,这样地层孔隙度就变成埋藏深度和经历时间的双元函数 (6式 )。这个函数属于二次曲线形式,相对比较复杂：

φ=αZ+bZt+ct+φ0

(6)

从(6)式中可以看出,在一个等速埋藏过程中孔隙度在受埋深影响的同时,也受到埋藏时间的影响,而且埋深与埋藏时间对孔隙度影响作用的级别是相同的。从这个意义讲,埋藏时间对孔隙度的影响作用是相当大的,相同埋深时不同埋藏时间所对应的孔隙度完全不相同。

由于地层沉积埋藏过程一般不为等速埋藏形式,埋藏过程变化比较复杂。但地层沉积埋藏过程总是按时间先后逐层叠加上覆地层,这样可以把一个埋藏速率变化复杂的埋藏过程视为若干个等速埋藏子过程的叠加,这样在每一个等速埋藏阶段其孔隙度变化就符合(6)式,即地层孔隙度是埋深和经历时间的双元函数。

5 讨论

砂岩压实作用对砂岩致密过程的影响是一个复杂的过程,本文以孔隙度为切入点将机械压实作用对砂岩致密过程的影响程度定量化,提出了地层孔隙度是埋深和经历时间的双元函数数学模型。由双元函数可知,只要沉积物开始沉积机械压实作用就一直存在,且随着埋深和埋藏时间的增加机械压实作用越来越强,因此机械压实作用对砂岩致密过程具有较大的影响。

与胶结作用相比,压实作用没有特定的时间、温度、压力和流体等诸多因素的限制而贯穿于成岩作用整个过程,尽管早期的胶结作用能为砂岩保存大量的原生孔隙空间,为之后的溶蚀作用提供大量的溶蚀空间,从而释放出孔隙空间大大改善了砂岩的储集性能。但一旦失去胶结物的支撑,上覆载荷产生的压实作用会导致溶蚀作用产生的次生孔隙大大减少,因而压实作用对成岩作用的影响程度超过胶结作用。

当考虑溶蚀产生的次生孔隙时,会存在如下3种情况：产生了较多次生孔隙的砂岩、产生了少量次生孔隙的砂岩以及不产生次生孔隙的砂岩。当上述3类砂岩处于同样的埋藏深度和埋藏时间时,溶蚀作用之后压实作用的压实程度一致还是存在差异？若是存在差异是哪一类砂岩压实程度大？这一问题有待于进一步的分析及研究。

6 结论

(1)井孔砂岩孔隙度变化趋势、砂岩镜下结构和压实模拟实验证实了机械压实作用一直存在于砂岩致密化过程中。

(2)压实作用是砂岩储层致密化最主要的原因,在致密减孔过程中压实作用对砂岩的影响程度要超过胶结作用产生的减孔效应。

(3)砂岩孔隙度受控于埋深和埋藏时间,通过建立定量计算压实作用减孔的双元函数模型,以孔隙度来定量分析压实作用对砂岩致密过程的影响程度。

致谢:感谢中石油“十二五”国家油气重大专项“岩性油气藏成藏动力、临界条件与分布模式”(编号 2011ZX05001-001-04)对本次研究的资助；感谢中国石油大学(北京)温顺久老师对薄片观察的帮助；感谢北京康普瑞基石油工程技术有限公司赵江青对双轴承压实验的帮助。