大型LNG储罐翻滚现象的预测模型研究

宋旦鹏，杜书成，李兆慈，孙恒

(1.华电郑州机械设计研究院有限公司，郑州 450015； 2.中国石油天然气股份有限公司天然气与管道分公司，北京 100007； 3.中国石油大学(北京)，北京 102249)

0 引言

大型液化天然气(LNG)储罐储存过程中，充注不当引起的分层是导致“翻滚”的直接原因，从而致使储罐内大量LNG迅速蒸发或泄漏，引发严重的安全事故，国内外对此已开展了大量的研究[1-6]。

在已有的预测模型中，如何计算通过上、下两层间分界面的传热、传质量对准确预测翻滚发生的时间有着重要影响。本文拟采用简单的大空间自然对流换热关联式确定通过分界面的传热、传质量，并希望在此基础上计算出罐内液体随储存时间变化的温度曲线、密度曲线等，使用户在使用中可以根据实际需要及时进行调整，在保证LNG储存安全的同时还可保证最佳的经济性。

1 模型

1.1 建立模型

本文模型的主要假设如下：LNG密度是组分和温度的函数；每层内密度、温度一致，是时间的函数。则控制方程如下。

(1)对下层液体。

质扩散：

d(nlxi)/dt=kA(yi-xi) ，

(1)

式中：n为物质的量，mol；x为下层液体的摩尔分数；y为上层液体的摩尔分数；t为时间，s；A为分界面面积，m2；k为质量扩散系数；下标l代表下层液体；下标i代表LNG的某一组分。

热扩散：

d(nlcplTl)/dt=hAΔT+Ql+Qml，

(2)

式中：cp为比定压热容，J/(kg·K)；T为温度，K；Q为漏热量，J；h为热量扩散系数；Qm为质量扩散引起的热量传递，J。

(2)对上层液体。

质扩散：

d(nuyi)/dt=-kA(yi-xi)+Vid(nu)/dt，

(3)

式中：V为气相空间体积，m3；下标u代表上层液体。

热扩散：

d(nucpuTu)/dt=-hAΔT+Qu-Qml+Qb，

(4)

式中：Qb为气化引起的热量传递，J。

(5)

当 (yi-xi)>0时，T=Tu；(yi-xi)<0时，T=Tl。

1.2 层间传热、传质与漏热模型

在式(1)～(5)中，需要确定的内容包括：气相空间至上层液体的传递热量；通过罐壁和罐底到上、下两层液体的漏热量；上、下两层液体之间的传热量和传质速率。

以往的预测模型[6]假设上、下两层间存在一个明显的分界面，但由于存在温度和密度2种梯度而形成稳定分层时，相邻两层液体之间会产生一个液-液界面，这种界面被称为双向扩散界面，它对两层液体间的传热产生很大的影响。

本文假设上层和下层液体间的热、质传递均通过中间的双向扩散界面进行，双向扩散界面相对稳定并近似于“平壁”，热量以自然对流的方式通过分界面。大型LNG储罐直径和罐高都有几十米，属于大空间自然对流换热，则上、下层间的换热量为

Ql_u=Ahl_in(Tl-Tin)=Ahin_u(Tin-Tu) ，

(6)

式中：hl_in为下层与中间层的自然对流换热系数；hin_u为上层与中间层的自然对流换热系数；下标in代表中间层。

可分别按大空间平壁热面朝上和冷面朝下计算

Nu=C(GrPr)n=C(Ra)n，

(7)

式中：Nu为努塞尔数；Gr为格拉晓夫数；Pr为普朗特数；Ra为瑞利数；C，n为常数。

由于热质交换同时存在，由准则关联式可以得到对流质交换系数

h/k=cpρ(Sc/Pr)2/3=cpρ(Le)2/3，

(8)

式中：Sc为施密特数；Le为路易斯数；ρ为密度，kg/m3。则有

k=h/[cpρ(Le)2/3] 。

(9)

1.3 离散方法

采用传递函数法对式(1)～(5)进行离散的方法已经得到比较广泛的应用。本文采用直接差分法对其进行离散，时间步长取为3 min，同样得到良好的效果。

2 计算结果与分析

采用上述模型对意大利LNG储罐“翻滚”事故进行了计算：LNG船在充注前已在终端停泊1个多月，所载LNG的密度和温度均有所上升。从储罐底部充注LNG时，由于新、旧LNG密度差为3.844 kg/m3，温度差为4.638 K，形成上、下两层。将LNG看作5种组分的混合物(C4以上组分按C4计算)，其参数见表1。

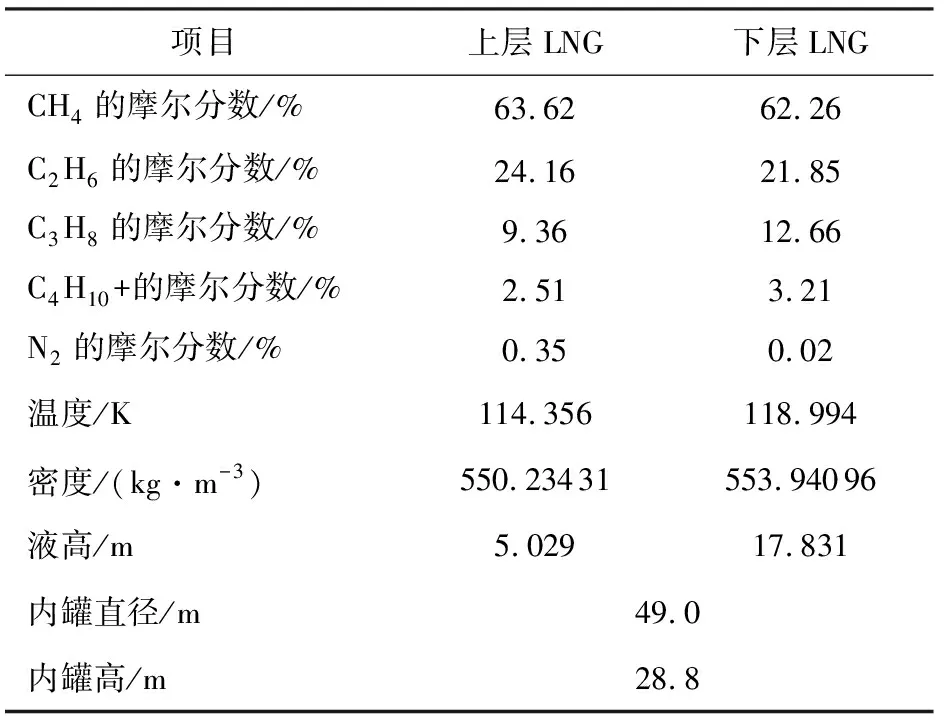
表1 上、下两层LNG参数

对上述算例进行计算，所得到上、下两层LNG温度、密度和组分随时间的变化，如图1～图5所示。从图中分析得出：

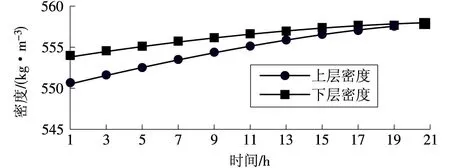
图1 LNG上、下两层密度随时间的变化

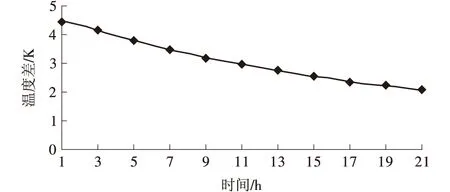
图2 LNG上、下两层温度差随时间的变化

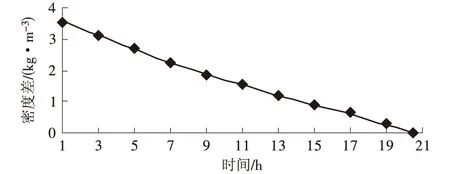
图3 LNG上、下两层密度差随时间的变化

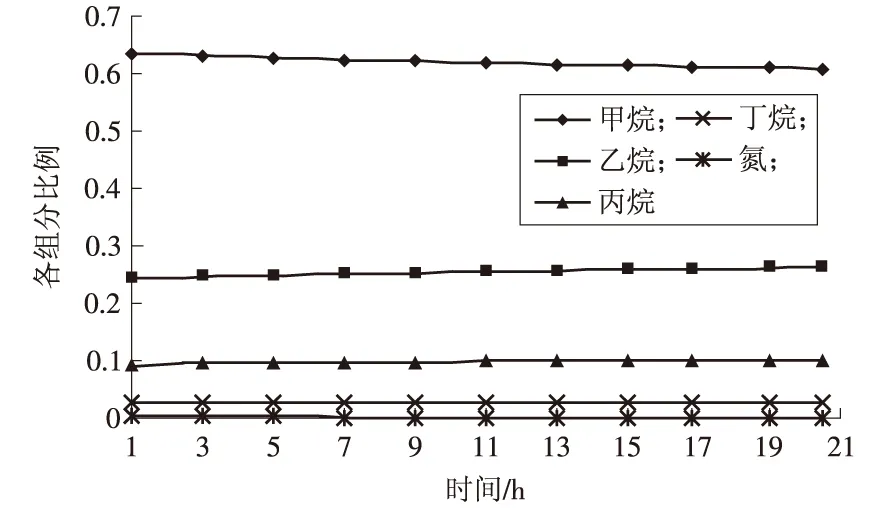
图4 LNG上层各组分随时间的变化

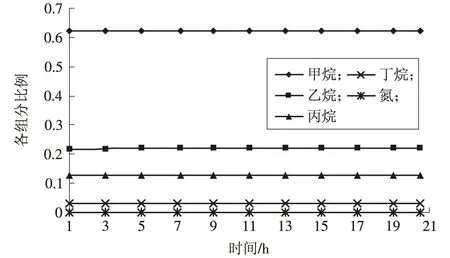
图5 LNG下层各组分随时间的变化

(1)上、下两层热、质交换时，密度差和温度差并没有同时变为0；

(2)下层各组分比例比较稳定，这是因为上、下两层通过扩散交换的质量很小。而上层各组分比例有较明显变化，这是因为甲烷和氮优先蒸发，引起上层各组分比例变化；

(3)当上、下两层密度接近时，翻滚发生，产生大量蒸发气体(BOG)，预测翻滚时间为21h，实际充注结束后18h发生翻滚，与文献[6]中的预测时间相比更接近实际情况。

3 结论

本文对大型LNG储罐充注不当引起分层后翻滚发生时间的预测模型进行研究，认为在各液层之间存在一个液-液分界面，各层液体之间的热、质传递均通过这个中间层进行双向扩散，并采用大空间自然对流关联式计算此传热、传质过程，获得了良好的效果。

参考文献：

[1]李品友,顾安忠.液化天然气涡旋及其预防措施[J].低温与特气,1998(2)：54-57.

[2]林文胜,顾安忠,李品友.液化天然气的分层与漩涡研究进展[J].真空与低温,2000(3)：125-132.

[3]游立新,顾安忠.液化天然气的分层和涡旋及防止措施[J].石油与天然气化工,1991,20(3)：21-25.

[4]程栋.液化天然气的贮存分层现象[J].深冷技术,1997(1)：13-15.

[5]覃朝辉,顾安忠. 液化天然气涡旋的模型研究[J].上海交通大学学报,1999,33(8)：954-958.

[6]S Bates,D S Morrison. Modelling the behaviour of stratified liquid natural as in storage tanks:a study of the rollover phenomenon [J].International Journal of Heat and Mass Transfer,1997,40(8)：1875-1884.