干扰条件下机载雷达对海探测距离数值计算分析

郭予并, 魏永峰

(91404部队，河北 秦皇岛066000)

干扰条件下机载雷达对海探测距离数值计算分析

郭予并, 魏永峰

(91404部队，河北 秦皇岛066000)

从雷达、干扰方程及海杂波基本模型出发，对有源干扰条件下机载雷达对海探测距离失真的成因进行了深入分析。通过仿真数值计算，揭示出不同背景环境下对目标探测距离变化规律，为指导实战运用提供合理可信的理论依据。

海杂波功率；雷达接收机功率；干扰功率

0 引 言

有源干扰条件下机载雷达对海上目标的探测，除了与所受到的有源干扰功率的大小、方位相关外，还与背景环境下的海面杂波干扰功率大小、方位有关。对海上目标距离的测算，由于有源干扰特征明显，往往忽略海杂波的存在。在远距离上这种忽略暂且可以视而不见，但在近距离上这种忽略有可能造成对海探测距离失真，从而影响武器系统打击效果。通过对比，本文深入分析无干扰、有干扰条件下对海探测距离的变化，给出不同距离、方位上干扰(有源+海杂波)对机载雷达探测距离的影响程度，揭示其影响变化规律，用数值仿真计算的方式对典型用例进行推演，从而为航空兵对海面目标突击训练及战术应用提供帮助。

1 无有源干扰条件下机载雷达对海探测距离分析[1-2]

1.1 海杂波分析

雷达在对海探测时将遇到强的海杂波，海杂波的存在将直接影响雷达的探测性能。海杂波功率为[1]

(1)

其中，Pt为雷达发射功率；Gt为雷达天线功率增益；λ为雷达工作波长；R为雷达距海面距离；LS为系统损耗；σc为产生海杂波的雷达截面积，σc=σ0Ac，σ0为表面后向散射系数，Ac为表面面积，这样：

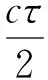
(2)

其中,ψ为入射余角或天线波束俯角，τ为雷达信号脉冲宽度，△φ3dB为天线方位3 dB波束宽度，c为光速。

故

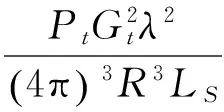
(3)

对海探测中，一般有如下3种不同情况：

(1) 在远距离，PC≪PN，PC的影响可以忽略，只需考虑接收机噪声对探测性能的影响；

(2) 在近距离，PC≫PN，PN的影响可以忽略；

(3) 在中间的一段距离，噪声功率和海杂波功率都要考虑。

1.2 自由空间中雷达探测距离

设雷达发射功率为Pt，雷达天线增益为Gt，目标与雷达天线的距离为R，目标散射截面积为σ，脉冲压缩比为D，雷达信号波长为λ，则在自由空间工作时，由基本雷达方程，雷达接收天线接收到的回波功率：

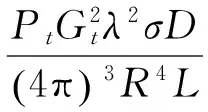
(4)

当Prs等于最小可检测信号功率Smin时，可得到雷达检测该目标的最大作用距离：

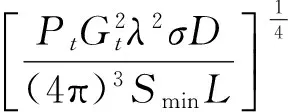
(6)

其中Smin可表示为

(8)

用检测因子D(n)表征检测目标信号所需的最小输出信噪比。则雷达方程为

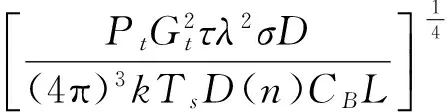
(9)

其中，τ=1/Bn为雷达信号脉冲宽度，CB为接收带宽修正因子。

1.3 雷达对海探测距离

机载雷达是在海杂波背景下检测海面上运动或静止目标的，海杂波对雷达检测性能的影响可以用等效噪声功率谱密度来表示。

雷达接收到的海杂波功率谱密度:

(10)

海杂波功率在雷达接收机输入端的等效噪声温度:

(11)

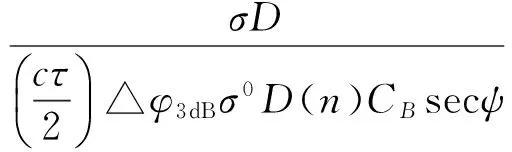
(13)

空中平台在高空飞行，对海探测距离较远时，PC≪PN，这时只需考虑接收机噪声对探测性能的影响，见式(9)。

2 干扰条件下机载雷达对海探测距离分析[3-4]

假设：有源干扰条件下，机载雷达、干扰机、目标配置关系如图1所示。

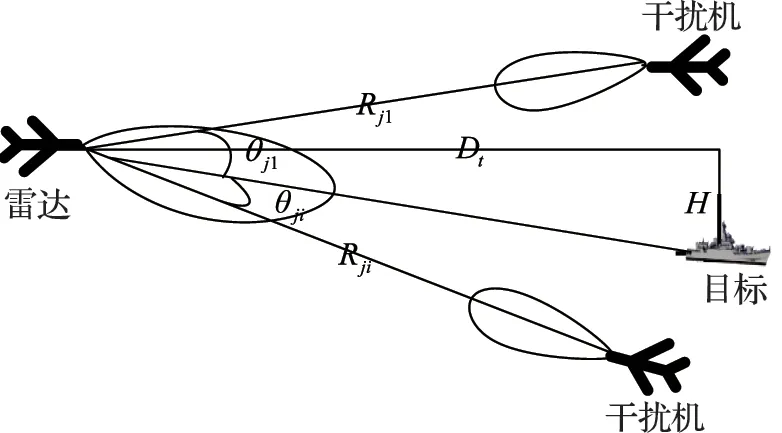
图1 雷达、干扰机、目标位置配置关系

雷达接收到的干扰信号功率为

(15)

其中,Pj为干扰机功率，Gj为干扰机天线增益，Gt(θ)为雷达天线在干扰机方向的等效增益，γj为极化失配损失，Rj为干扰机至雷达的距离。

有源干扰信号的带宽通常大于接收机的信号带宽，可以用等效噪声功率谱密度Nrj来表示。

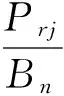
(17)

干扰功率在雷达接收机输入端的等效噪声温度Tj可表示为

(18)

(19)

有源干扰条件下的雷达方程仍为

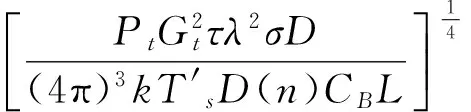
(20)

或

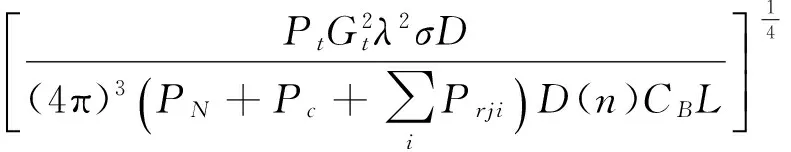
(21)

代入得

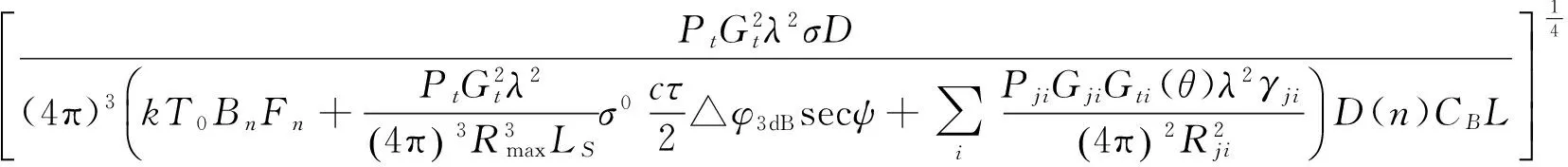
(22)

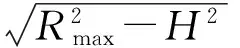
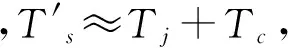
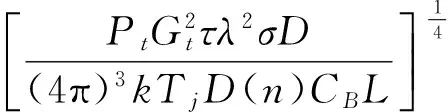
(23)

亦即

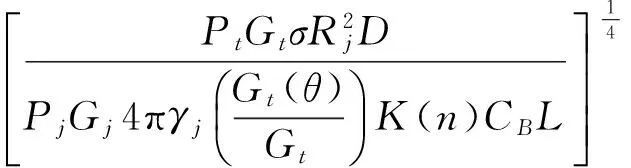
(25)

3 机载雷达对海探测数值计算用例[5-6]

假设：机载雷达参数设为Pt=400 W，Gt=33 dB，λ=0.112 m，τ=0.2 μs，脉冲压缩比D=60，k=1.38×10-23W/(Hz)(K)，△φ3dB=0.01534 rad。D(n)CB=2，T0=290 K，Fn=10，L=4 dB，c=3×108m/s。

3.1 无干扰条件下机载雷达对海探测距离计算

(1) 无干扰条件下不考虑海杂波机载雷达对海探测距离计算

考虑到检测因子，在不考虑海杂波的情况下，由式(9)计算σ=3000 m2时的雷达对海探测距离见表1。

(2) 海杂波功率计算

平台高度为H，R=H/sinψ，由式(3)分别计算ψ=10°、ψ=1°、ψ=30°时飞机位于不同高度的海杂波功率，如表2、表3、表4。

从中看出,ψ=30°、平台高度在5000 m以下时,PC≫PN，雷达对海探测距离最远不超过10 km,属于近距离，PN的影响可以忽略。

ψ=1°或ψ=10°、平台高度在2000 m以上时，PC≪PN，PC的影响可以忽略。

ψ=10°、平台高度在2000 m以下或ψ≥30°时，PC与PN相当，噪声功率和海杂波功率都要考虑。

表1 不考虑海杂波情况下不同雷达反射面积雷达对海探测距离

表2 ψ=10°时海杂波功率(三级海况，σ0=-46 dB)

表3 ψ=10°时海杂波功率(三级海况，σ0=-48 dB)

表4 ψ=30°时海杂波功率(三级海况，σ0=-38 dB)

(3) 无干扰条件下考虑海杂波机载雷达对海探测距离计算

求飞机位于10000 m高时的雷达对海探测距离。因为ψ=10°、ψ=1°时PC≪PN，海杂波对雷达对海探测距离不造成影响，只由噪声功率决定。而ψ在30°左右及以上时，PC与PN相当，故可取σ0=-38 dB。由式(12)得

代入求得方程式如下：

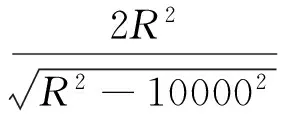
=1.997×107×60×σ

(26)

通过数值计算方法近似求解，部分解如表5所示。

表5 考虑海杂波情况下不同雷达反射面积雷达对海探测距离

3.2 干扰条件下机载雷达对海探测距离计算

干扰机参数设为：PjGj=105W，λ=0.112 m，θ0.5=1°，K=0.04，γj=0.5，Rj=300000 m，Gt=33 dB。

(1) 有源干扰功率计算

由式(15)，分别计算θ≥90°、θ=45°、θ=15°、θ=0°时的雷达接收的有源干扰功率如表6。

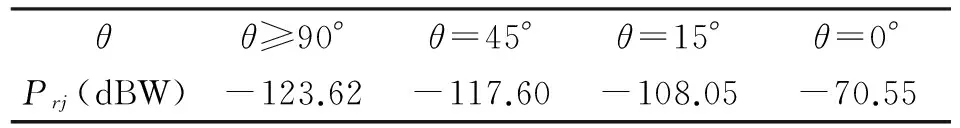
表6 雷达接收有源干扰功率

(2) 对海探测距离计算

当主瓣干扰和θ≤45°副瓣干扰时，雷达接收的有源干扰功率远大于接收机噪声功率、海杂波功率，对海探测距离主要受干扰功率影响。

当θ≥90°副瓣干扰时，雷达接收的干扰功率与接收机噪声功率、海杂波功率相当，接收干扰功率、噪声功率和海杂波功率都要考虑。由式(22)求得方程式如下：

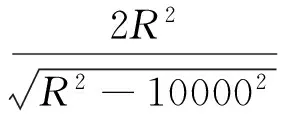
=1.997×107×60×σ

(27)

部分解如表7。如表7可知，在同样的距离上，考虑海杂波但不考虑有源干扰时能探测到的目标反射面积要小于考虑海杂波和有源干扰时能探测到的目标反射面积，大于不考虑海杂波和有源干扰时能探测到的目标反射面积，这与有源干扰和海杂波均影响机载雷达对海探测的定性分析是相符的。

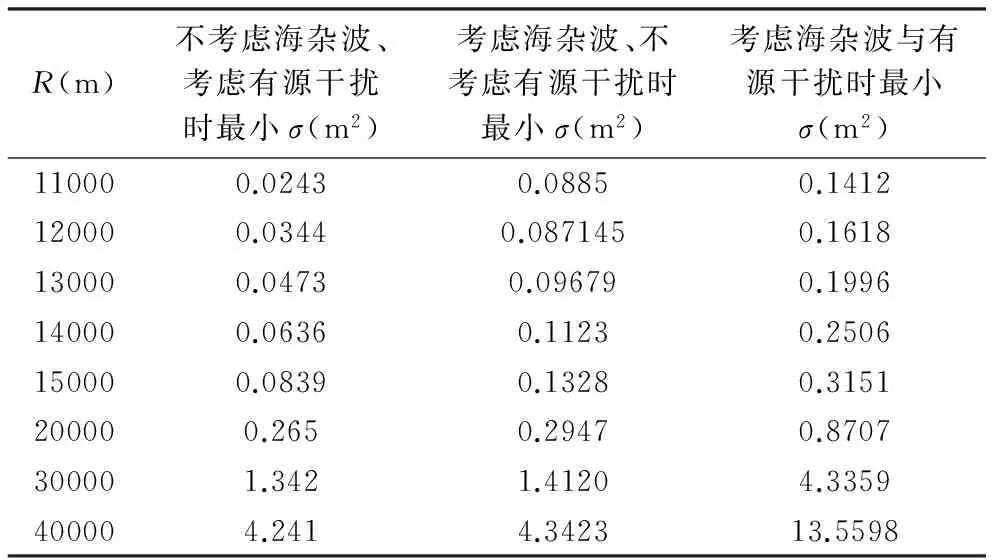
表7 考虑副瓣干扰与海杂波时雷达探测距离近似计算值

4 结束语

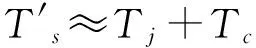
[1] 贲德，等.机载雷达技术[M].北京：电子工业出版社，254，271，288-290.

[2] 丁鹭飞.雷达原理[M].西安：西安电子科技大学出版社，2009.3.

[3] 赵国庆. 雷达对抗原理[M]. 西安：西安电子科技大学出版社，2012.10.

[4] 罗景青. 雷达对抗原理[M]. 北京：解放军出版社， 2003.4.

[5] 张锡祥. 新体制雷达对抗导论[M]. 北京：北京理工大学出版社， 2010.1.

[6] 邵国培，等. 电子对抗作战效能分析[M]. 北京：解放军出版社， 1998.2.

Numerical calculation and analysis on detection range of sea targets for airborne radars with interference

GUO Yu-bing, WEI Yong-feng

(Unit 91404 of the PLA, Qinhuangdao 066000, China)

The causes that result in distortion of the detection range of sea targets for the airborne radar with active jamming are analyzed in terms of radar, jamming equation and basic models of sea clutters. The change rules of the detection range under different conditions are unveiled through the numerical simulation, which provide the reasonable and credible theoretical basis for actual combat.

sea clutter power; radar receiver power; jamming power

2014-10-27

郭予并(1965-),男,高级工程师,研究方向：雷达指控试验。

TN959.73

A

1009-0401(2014)04-0005-04