开槽应力释放法优化整体结构件切削加工研究
刘秦龙,华 军,贾瑞艳
(西安建筑科技大学理学院,陕西西安 710055)
随着现代机械高速高机动性能不断提升,机械构件强度与韧性要求不断提高,机械构件日趋偏重于整体结构加工。但是在整体结构件加工过程中,由于毛坯初始残余应力释放引起的变形严重影响加工精度[1]。因为涉及国防关键性技术,所以尽管发达国家对切削加工中变形控制做了大量研究,但其研究成果皆属机密。而我国对其研究仍处于起步阶段,与发达国家相比依然存在不小的差距[2]。
开槽应力释放法是切削加工前,在毛坯件中开槽释放毛坯件中初始残余应力,减小由其引起变形的方法。开槽法应力释放机理复杂,研究资料稀缺,文献[3]、[4]中对于开槽法理论的解释仅限于几何推导层面,没有明确解释开槽法的作用机理。
本文从力学角度建立单一方向残余应力下开槽法力学模型,解释开槽法机理,建立毛坯件开槽法有限元模型,通过模拟运算对开槽法工艺进行讨论,为开槽法优化加工工艺提供理论依据。
1 开槽法简介
对于高强度铝合金板,其单向残余应力沿厚度方向分布。本文遵从如下假设:
a.铝板各向同性,材质均匀连续。
b.应力与应变线性相关,弹性模量不变。
c.残余应力仅沿板厚方向变化,在平行于板中面的任一平面内均匀分布且对称于中面(厚度方向几何中性层面即厚度中点所在面)。
开槽前板内残余应力处于平衡状态,开槽后其内部残余应力的平衡状态被打破,整体构件的初始残余应力由于开槽而释放,宏观表现为翘曲变形。在后续的加工工序中可以在开槽毛坯件背面进行加工,加工时背面残余应力释放,引起的变形将会抵消之前开槽引起的变形,降低整体构件内部的残余应力水平,最终减小构件的变形。
2 拱高理论推导
文献[3]、[4]中给出的拱高公式从开槽后构件几何变形角度推算拱高值,其关键参数——曲率半径很难测得,限制了该公式的应用,因此有必要从力学角度推导变形拱高公式。
假设毛坯件纵剖面如图1所示,初始曲率为0,长度为 (L1+L2+L3),厚度为h。L1与L2段为未开槽段,L3为开槽段,槽位于毛坯件正中,t为单层切削层厚度,b为毛坯件宽度。
由于L3段材料的去除打破了应力平衡,引起构件变形。图中σ1,σ2,σ3为开槽之后引起的反向等效应力[5],其大小与文献[6]中的残余应力分布曲线等值反向。L3段简化为两端简支的欧拉-伯努利梁,而L1段与L2段未被切削,可以认为段内应力分布依然自平衡,所以L1与L2段只是随L3段变形而产生转动。L3段拱高可由材料力学公式[7]给出:
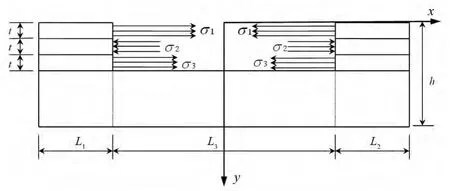
图1 开槽法力学模型

式中:M为开槽所引起的等效反力对L3段中性面的弯矩;I为L3段的截面惯性矩。其计算式分别如下:

式(2)中:M由残余应力分布函数σ与开槽深度y复合而成,其中残余应力分布函数σ通过实验拟合,是仅含自变量y的函数。因此一旦开槽深度y确定,M将会随之确定。同时,式(3)中变量只有开槽深度y,因此当y确定时I亦随之确定。再将式(2)、(3)代入式(1)得出变形拱高w,其与开槽宽度L3的平方成正比,可据此初步校核有限元模型的可靠性。但是当y变化时,式(2)中σ随y变化而变化,无法确定M,此时通过离散残余应力分布曲线确定y与σ(即在图2所示残余应力分布曲线中给定y值并查找对应σ),再求解M与I,同样代入式(1)中可以求解出w,以校核数值模拟模型的正确性。在基于上述两类数据判定有限元模型可靠性后,再采用有限元模型进行开槽加工优化。
3 数值模拟
开槽过程利用有限元软件的单元生死[8]来实现。有限元模型取材为国产T7075铝材,密度为2 780kg/m3,弹性模量 E=71GPa,泊松比为 0.33。模型尺寸为130mm×90mm×45mm,选取Solid185单元。为只约束其整体刚体平动,分别在其3个角点约束 XYZ、XZ、Z 方向自由度[3]。
根据“力平衡,力矩平衡”的原则离散残余应力分布曲线[6]。20个离散点均布于厚度方向。有限元模型也相应地分成20层,各层应力值对应于各离散点值,如图2所示。模型布槽与理论模型一致,为中心对称通槽。
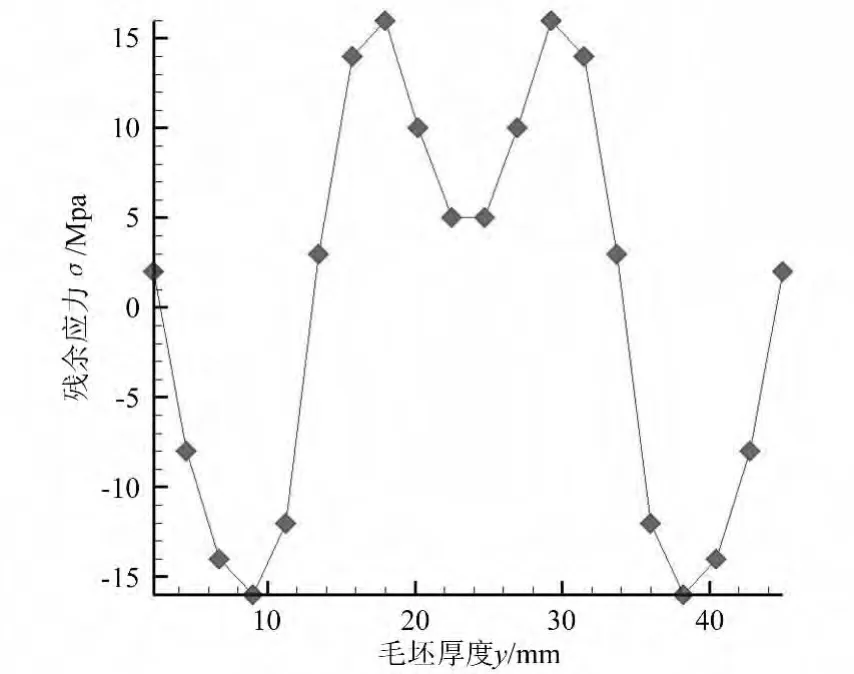
图2 残余应力离散曲线
通过理论与模拟两种不同方式分别计算拱高值,得到如图3,4所示拱高曲线。两图中理论与数值模拟曲线均走向一致,大小吻合,表明理论模型结果与模拟结果一致。
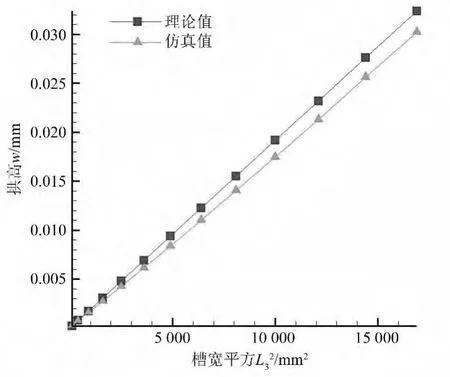
图3 槽深15.75mm时槽宽平方-拱高曲线

图4 槽宽10mm时槽深-拱高曲线
图3中曲线符合公式(1)中“M与I为常量时w与L3的平方成正比”。图中数值模拟结果与理论计算结果吻合,有限元模型合理。
4 开槽效果影响因素分析
实际加工中,开槽宽度与开槽深度为开槽加工的基本参数,直接影响开槽效果;而由于设计构造原因,应用开槽法时需要通过控制走刀方向与开槽数目来满足加工要求,因此对开槽走向与开槽数目的优化尤为重要。本文通过对铝合金毛坯件不同开槽方式所产生的变形拱高数据进行收集,分析不同开槽深度、宽度、走向、数目对变形拱高的影响,以得到较优化的加工方案。为切合实际工况,本文采用整体变形值Wf来表征拱高变形程度,即为满足变形协调关系,未开槽段转动,导致开槽部分发生刚体平动的位移值与拱高变形值的叠加值。
4.1 槽深
图5中曲线走势先下降后上升,表明在开槽宽度确定时,变形拱高并不随槽深单调变化,而是在变形达到一定限度时出现回弹,抵消之前的变形。拱高在开槽深度达到27mm之前逐渐增大,变化比较平缓,由式(1)可知,这是因为开槽部分拱高变形主要取决于作用于其上的弯矩M和其截面惯性矩I的比值,此时开槽部分截面惯性矩I比较大,二者比值变化平缓,拱高变形对于槽深变化不敏感。在槽深超过27mm之后变形拱高开始反弹,这是由于残余应力作用于开槽部分弯矩反向变化引起的;同时变形速率快速增加,由式(3)知随着开槽深度y增加,L3段截面惯性矩I急剧减小,导致拱高变形对槽深变化敏感。当槽宽在20mm和30mm时,同样可以观察到类似的曲线。

图5 槽宽10mm时槽深-变形曲线
4.2 槽宽
开槽时从10mm槽宽开始等步长增加开槽宽度,记录变形量,绘制成图6。图6表明在同一开槽深度下,拱高变形与开槽宽度近似呈抛物线关系,存在变形最大点,一旦超过该点变形就缓慢反弹,抵消之前开槽引起的变形。这符合在公式(1)中M与I确定时拱高w为槽宽L3的二次函数。在槽深为11.25mm、31.50mm、36.00mm 的情况下同样获得了类似曲线。
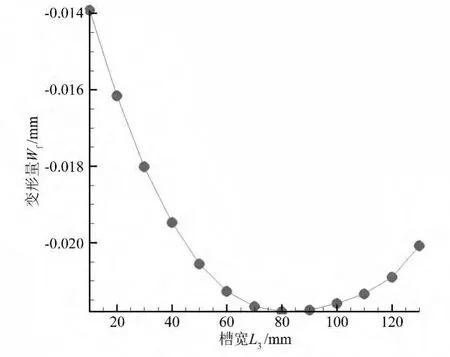
图6 槽深20.25mm时槽宽-变形曲线
4.3 开槽走向
开槽尺寸为纵槽30mm×10mm,横槽10mm×30mm,矩形槽中心位于毛坯件几何中心,两种开槽方式中横纵向分别与毛坯件横向(纵槽)、纵向(横槽)垂直,深度皆为15mm。变形数据如图7所示。

图7 开槽走向对变形的影响
图7 中横槽引起的变形拱高比纵槽的大幅增加,表明在同等条件下,开横槽释放残余应力的效果要优于纵槽。在槽深为11.25mm、31.50mm、36.00mm的情况下也得到相同的结论。因此,在实际加工中相同位置去除等量的材料时,应优先选用横槽。
4.4 开槽数目
选取单槽尺寸都为横槽10mm×30mm,深度15mm,分别均匀开4槽与8槽,图8为8槽布槽图,4槽布槽与之相类似。从图9中的数据对比可知,8槽变形大于4槽,应力释放更加充分。在深度11.25mm、31.50mm、36.00mm 情况下同样有此结论。因此在工况允许的情况下,应当充分开槽释放构件残余应力。

图8 横向8槽
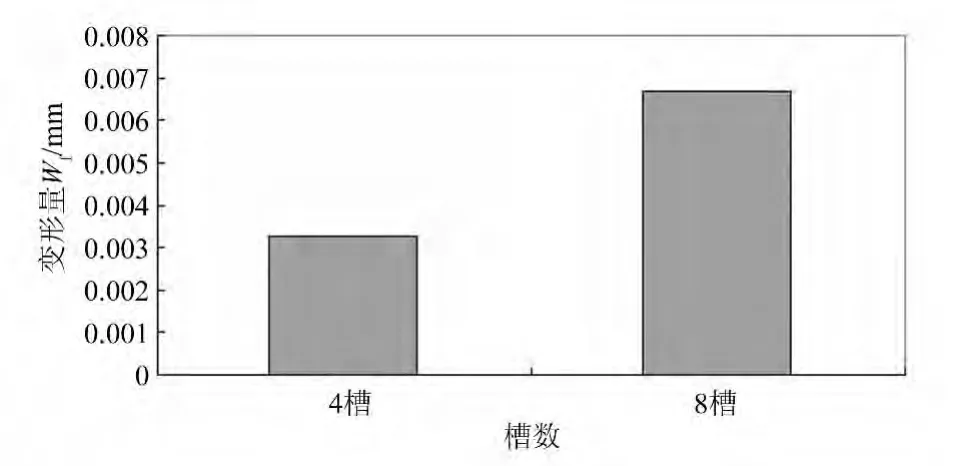
图9 开槽数对变形的影响
5 结论
a.开槽深度对残余应力释放有重要影响。开槽深度在残余应力分布中性面以上时,开槽越深,构件的变形越大,变形速率较为平缓;在深度超过中性层面时,变形量随开槽深度增加急剧回弹;构件在开槽过深时甚至产生反向变形。因此实际加工中需严格控制开槽深度,开槽深度不宜超过中性层面,开槽时应在毛坯件中性面附近开槽,以最大化释放残余应力。
b.开槽宽度对应力释放有重要影响。开槽深度确定时,开槽宽度与变形量近似呈二次关系,开槽时应当注意宽度控制,实际加工中开槽宽度应控制在总宽度的2/3以内为宜。
c.开非通槽时槽的走向对应力释放有影响。开同等量横槽效果要优于纵槽,实际开槽方案设计时应首选开横槽以达到应力最大化释放,去除等量材料开槽时应尽量开横槽。
d.开槽数目对应力释放有影响。开槽的数目越多,构件应力释放越多,变形越大,开槽效果越好。因此在构件的前期开槽中,应当在满足设计要求的前提下充分开槽,以完全释放毛坯件内部残余应力,减小后续加工中的变形。
[1] 董辉跃,柯映林,孙杰,等.铝合金厚板淬火残余应力的有限元模拟及其对加工变形的影响[J].航空学报,2004,25(4):429-432.
[2] 马海龙,段辉,汤爱君.薄壁零件切削变形的研究现状综述[J].机床与液压,2010,38(9):117-119.
[3] 马海营,何宁,李亮,等.基于开槽法的毛坯内应力释放数值研究[J].中国制造业信息化,2010,39(7):30-33.
[4] 马海营.基于开槽法的航空构件加工变形控制技术研究[D].南京:南京航空航天大学,2010.
[5] 袁发荣,伍尚礼.残余应力测试与计算[M].长沙:湖南大学出版社,1987:37-42.
[6] 王树宏.航空铝合金厚板初始残余应力及其对铣削变形影响的基础研究[D].南京:南京航空航天大学,2005.
[7] 孙训芳,方孝淑,关来泰.材料力学[M].北京:高等教育出版社,2009:165-169.
[8] 王立涛,柯映林,黄志刚,等.航空结构件铣削残余应力分布规律的研究[J].航空学报,2003,24(3):286-288.

