Active control of structural sound radiationin an acoustic enclosure consisting of flexible structure

Chen Dalin Chen Nan

(School of Mechanical Engineering, Southeast University, Nanjing 211189, China)



Active control of structural sound radiationin an acoustic enclosure consisting of flexible structure

Chen Dalin Chen Nan

(School of Mechanical Engineering, Southeast University, Nanjing 211189, China)

The active control of structural sound radiation in an acoustic enclosure is studied by using distributed point force actuators as the secondary control force, and the control mechanisms for the radiated noise in the cavity are analyzed. A rectangular enclosure involving two simply supported flexible plates is created for this investigation. The characteristics of the primary and secondary sound field and the structural-acoustic coupled system are analyzed, and the optimal control objective for reducing the sound pressure level (SPL) in the cavity is derived. The response of the SPL in the cavity is analyzed and compared when the secondary point force actuators with different locations and parameters are applied to the two flexible plates. The results indicate that the noise in the cavity can be better controlled when some point force actuators are applied to two flexible plates for cooperative control rather than the point force actuators being only applied to the excited flexible plate.

active control; acoustic mode; radiated noise; control mechanism; sound pressure level (SPL)

The study of the active control of structural sound radiation in the enclosure cavity is popular, for example, its application in the reduction of noise levels in aircraft fuselages or vehicle cabins[1-2]. Pan et al.[3]demonstrated that the optimal control of radiated noise in the enclosure does not only depend upon the strength of the control forces but also upon the location of the actuators and other parameters. Kim et al.[4]presented an analytical and experimental investigation into the active control of harmonic sound transmission in a structural-acoustic coupled system. They indicated that the number of control actuators must be equal to the number of modes being controlled[5-8]. Many researchers consider that the radiated noise in the interior can be well controlled by locating the actuators only on the excited flexible plate surface, but sometimes the noise cannot be well reduced at these frequencies which are dominated by the coupled plates. So we consider that we can put some point force actuators on both the excited plate and the coupled plate to minimize the SPL in the cavity.

A rectangular enclosure with two simply supported flexible plates and four rigid walls is used as a model for this investigation. Some equations for the sound field in the cavity and the structural vibration field in the panel are used to represent the system behavior, and Green’s function technique and boundary integrations are used to describe the sound pressure distribution in the cavity and the panel velocity distribution. The response of the SPL in the cavity is analyzed and compared with different control strategies used to reduce the radiated noise.

1 Analytical Model and Formulation

The panel-cavity system is used for this investigation (see Fig.1). The dimensions of the cavity areLX=0.868 m,LY=1.150 m,LZ=1.0 m. The top and right aluminum panels are simply supported and their thicknessesh=0.006 m. The primary point forceFpis expressed as the actuator locations and the complex force amplitudes, and the control point force actuators are described by the locations, numbers and the complex force amplitudes.

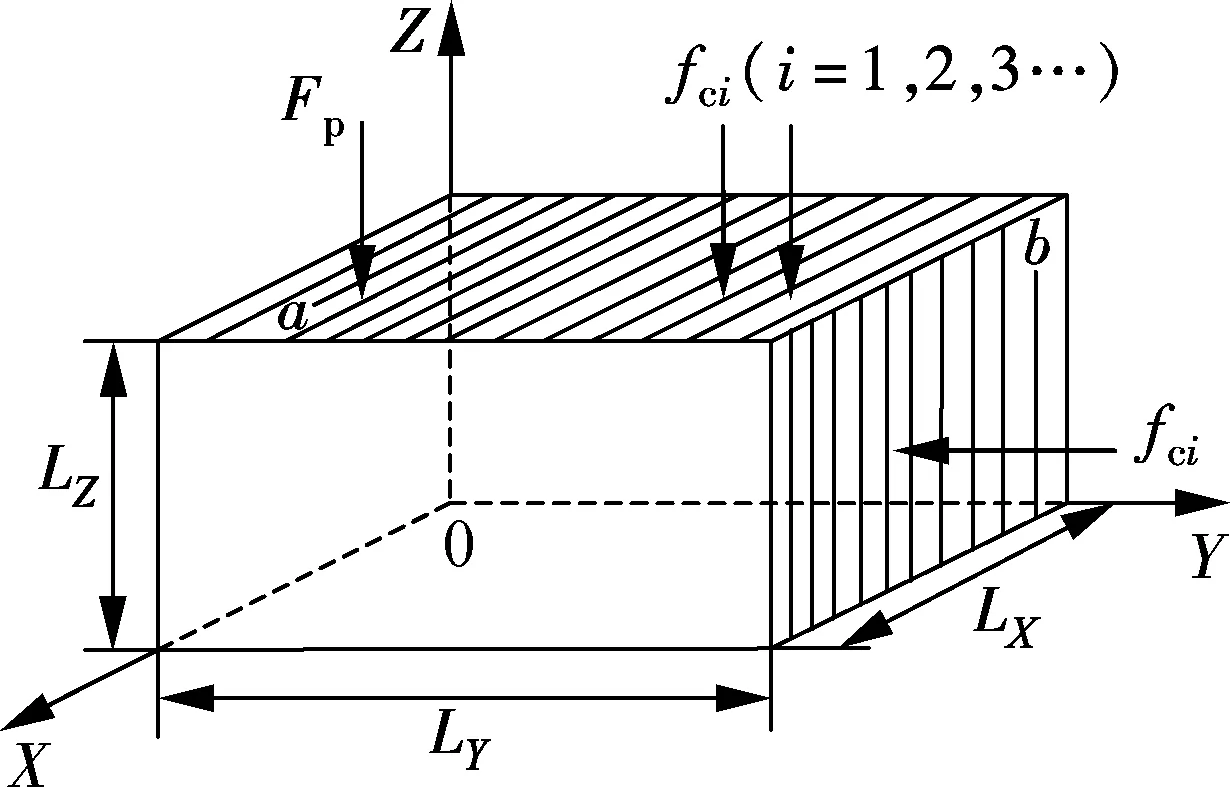
Fig.1 Enclosure geometry

The sound pressurepin the cavity is described as

(1)

whereδ(·) is the Dirac delta function;c0is the speed of sound in air;ρ0is the air density;waandwbare the normal displacement of panelaandb;vaandvbare the vibration velocity of panelaandb;σidenotes thei-th point force applied at position on the surface of platea. For the thin isotropic panelaand panelb, the flexural vibration equations are

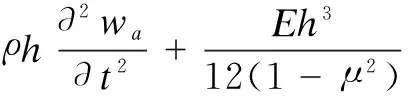
(2)

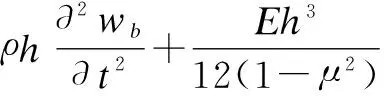
(3)

whereρ,E,μ,hare the density, Young’s modulus, Poisson’s ratio and the thickness of the panel, respectively. The Green functions are used to describe the sound field in the cavity and the vibration on the panel[3], and the sound pressure can be expressed as

p(r,ω)=jρ0ω∫AfGAv(r0,ω)dr

(4)

(5)

(6)

(7)

(8)

whereAfis the flexible panel surface area;riis the position in the cavity;ωis the angular frequency;GAis the Green function for the sound field;M2mis the cavity modal mass,kis the wave number in air;kmis the wave number of them-th cavity mode;φm(r) is the mode shape of the rectangular cavity;knis the wave number of then-th panel mode;ψn(σ) is the panel mode shape;Gsis the Green function for the simply supported panel;M1nis the panel modal mass. The panel velocity at locationσcan be expressed as

(9)

According to the modal synthesis method, the interior sound pressure and the panel velocity can be written as

(10)

(11)

Substituting Eq.(10) into Eqs.(4) and (9), we can obtain

P=ZAVm

(12)

Pext=ZsVm

(13)

whereVmis the panel velocity distribution;ZAis the internal modal radiation impedance matrix of the panel; andZsis the panel model input impedance matrix[3];Lnmis the modal coupling coefficient between them-th cavity mode and then-th panel mode. Here,Lnmcan be written as[9]

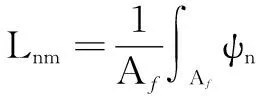
(14)

The modal amplitude of the primary sound pressure vectors due to the forceFpis given by

(15)

The sound pressure in the cavity without the influence of the point force actuators can be written as

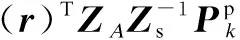
(16)

When some point force actuators are applied on flexible plates, and these actuators are located atσk, the secondary sound pressure in the cavity can be written as

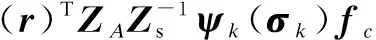
(17)

The total sound pressure in the cavity can be expressed by the linear superposition of the primary and secondary sound pressure

ptotal=pp+ps

(18)

The SPL is used to calculate the effect of constructing the acoustic pressure within the enclosure. The SPL and the panel averaged velocity can be written as

(19)

(20)

2 Results and Discussion

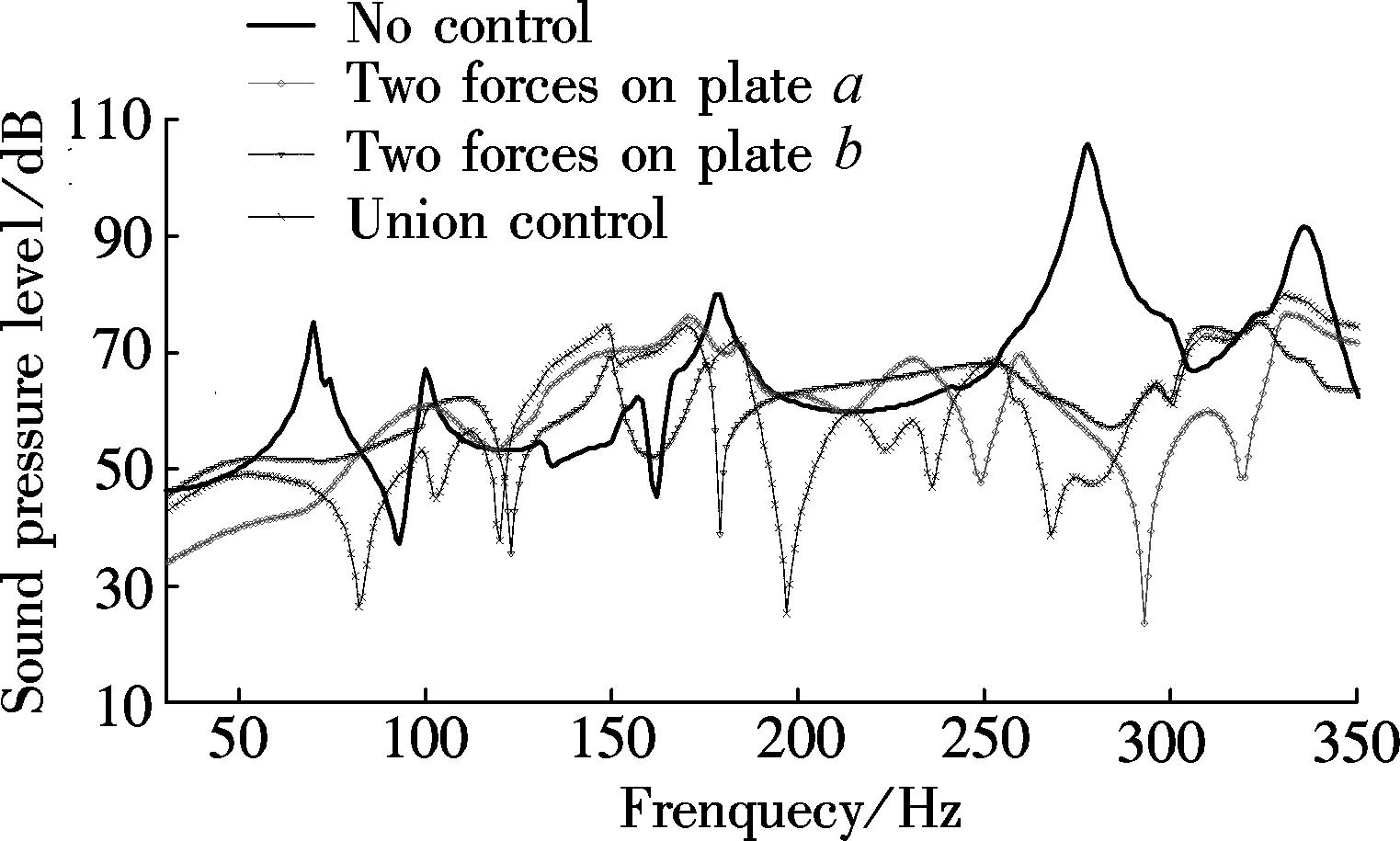
Numerical analyses are conducted using the configuration shown in Fig.1. The model parameters are as follows:ρ0=1.21 kg/m3,ρ1=2 700 kg/m3,E=68.5 GPa,η1=η2=0.01,μ=0.33,c0=344 m/s,c1=6 260 m/s. The primary unit harmonic forceFpis located at (0.3 m, 0.4 m) on platea. We take some control strategies to reduce the SPL in the cavity. First, we obtain the optimal location of each actuator, and then we use multiple actuators that are located on two flexible plates to obtain better control effort.

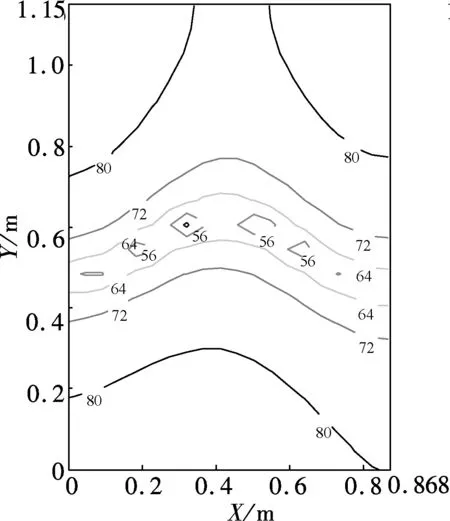
The region that we obtain the best noise control effort is just near the middle of the cavity. So we choose the region aroundSpoint at the coordinate (0.4 m, 0.5 m, 0.5 m) to analyze the control effort.

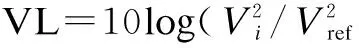
(a)

(b)

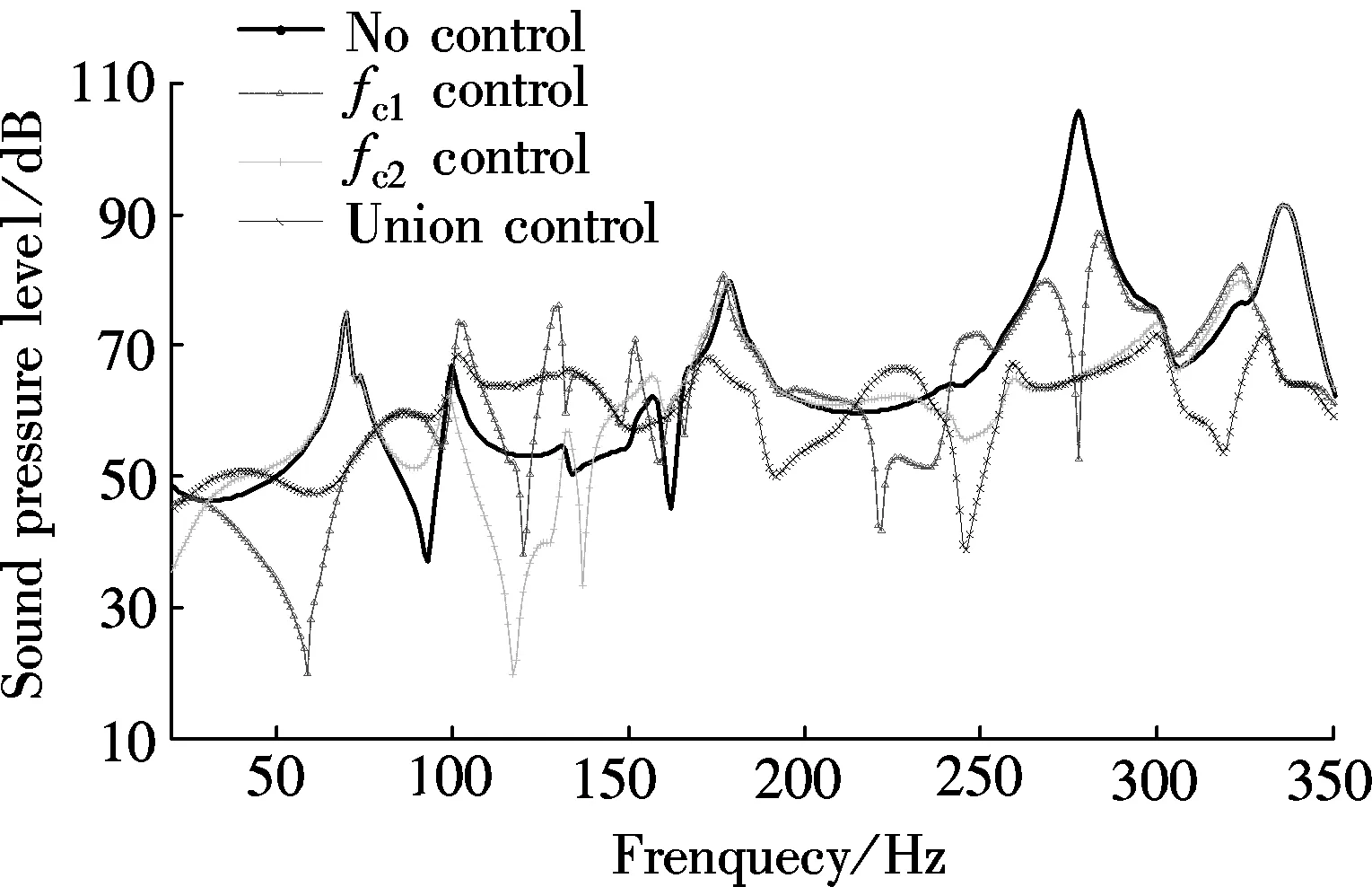
However, the noise interior is still high at 118, 184 and 252 Hz. Consequently,fc2is used to control the SPL in the interior at these frequencies. According to the VL equations and the rules on how the location offc1is selected, we obtain the location offc2at the high VL region. Fig.3(c) indicates that there are four regions where the VL is high on the plate.fc2is located at (0.5 m, 0.7 m) in the region that is diagonal fromFp. We can see that the SPL in the cavity is reduced by more than 20 dB at 118 and 252 Hz whenfc2is functioning. The results indicate that when the response noise is dominated by panel-controlled modes,

(a)

the sound pressure level in the cavity is minimized by suppressing these pane modes.

However, when the union control offc1andfc2are having an effective functioning, the noise reduction at 91 and 135 Hz is small, and the SPL is increased at some frequencies. As platebplays a leading role to the cavity noise at these frequencies, we need some new control mechanisms. So we consider to set some point force actuators on platebto reduce the SPL in the cavity.

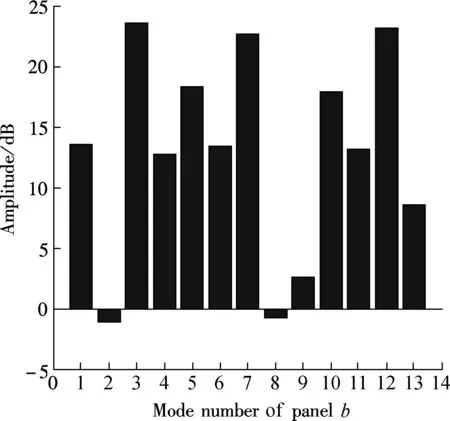
Fig.2(b) and Fig.4(a) indicate that the 3th, 7th and 12th structural modes of platebplay a contributing role to the noise in the cavity when the primary forces are located on platea. Sofc3is located at (0.72 m, 0.25 m) on panelb, andfc4is located at (0.72 m, 0.75 m) on panelb. Fig.2(b) shows that when there are two forces on panelb, the noise reduction is approximately 10 dB at 91 Hz and 135 Hz. It can be found that the cooperative control effect on panelaand panelbis better than only the control forces located on platea, as shown in Figs.2(a) and (b). Also, it can be seen that the SPL in the cavity is reduced at 172 Hz which is resonated by the cavity acoustic, and we can predict that when the noise is dominated by cavity-controlled modes, the control forces on panelbare used to change the panel velocity distribution and adjust the radiation of each panel mode for reducing the noise in the cavity.

(a)

Meanwhile, the increase of the SPL can reach 20 dB merely at 149 Hz, which is the resonant frequency of panelband the cavity acoustic. Fig.4(b) indicates that the 1st modal amplitude of acoustic plays a less important role when the primary force actuator is working on panelaatf=274 Hz. So the noise in the cavity can be better controlled when the control point force actuators are applied to two flexible plates for cooperative control.

3 Conclusion

The theoretical model of sound radiation in an enclosure surrounded by two flexible plates has been formulated. The simulations indicate that the excited flexible plate plays an important role for the noise in the cavity, and the coupled flexible plate also has some influences on the noise. The optimal control actuator location is obtained by the modal analysis method and contour plots; and multiple actuators are used on two flexible plates to reduce the SPL in the cavity. The results indicate that the cooperative control can obtain better control effects rather than the point force actuators that are only applied to the excited flexible plate.

[1]Hill S G, Tanaka N, Snyder S D. A generalized approach for active control of structural-interior global noise [J].JournalofSoundandVibration, 2009, 326(3/4/5): 456-475.

[2]Li Y Y, Cheng L. Active noise control of a mechanically linked double panel system coupled with an acoustic enclosure [J].JournalofSoundandVibration, 2006, 297(3/4/5): 1068-1074.

[3]Pan J, Hansen C H, Bies D A. Active control of noise transmission through a plate into a cavity: Ⅲ. effect of the actuator location [J].JournalofAcousticalSocietyofAmerica, 1991, 90(3): 1493-1501.

[4]Kim S M, Brennan M J. Active control of sound transmission into an acoustic enclosure using both structural and acoustic actuators [J].JournalofAcousticalSocietyofAmerica, 2000, 107(5): 2523-2534.

[5]Cui Huaifeng, Chen Nan. Active control of sound radiation and transmission into a cavity consisting of multi-flexible plates [J].NoiseControlEngrJ, 2012, 60(5): 492-506.

[6]Tanaka N, Takara Y, Iwamoto H. Eigenpairs of a coupled rectangular cavity and its fundamental properties [J].JournalofAcousticalSocietyofAmerica, 2012, 131(3): 1910-1921.

[7]Du J T, Li W L, Xu H A. Vibro-acoustic analysis of a rectangular cavity bounded by a flexible panel with elastically restrained edges [J].JournalofAcousticalSocietyofAmerica, 2012, 131(4): 2799-2810.

[8]Mohammad J I, Elliott S J. The performance of active control of random noise in cars [J].JournalofAcousticalSocietyofAmerica, 2008, 123(4): 1838-1841.

[9]Al-Bassyiouni M, Balachandran B. Sound transmission through a flexible panel into an enclosure: structural—acoustics model [J].JournalofSoundandVibration, 2005, 284(1/2): 467-486.

弹性结构封闭空间中结构辐射噪声的有源控制

陈大林 陈 南

(东南大学机械工程学院, 南京 211189)

研究了利用分布式点力源作为次级力源对封闭空腔内的结构辐射噪声进行控制的问题,并对封闭空腔中结构辐射噪声的控制机制进行了分析.建立了包含2块简支弹性板的矩形封闭空腔，并将其作为研究对象.通过对初、次级声场以及结构-声耦合的特性分析,以减小腔内声场的声压级为最优控制目标,分析比较了在不同位置及参数的次级点力激励下腔内声场的声压级响应.仿真结果表明，在2块弹性板上施加联合激振力控制腔内噪声的效果要明显好于激振力只作用在受激弹性板上.

有源控制;声模态;辐射噪声;控制机制;声压级

TB535

The National Natural Science Foundation of China (No.50975047).

：Chen Dalin, Chen Nan. Active control of structural sound radiation in an acoustic enclosure consisting of flexible structure[J].Journal of Southeast University (English Edition),2014,30(3):318-322.

10.3969/j.issn.1003-7985.2014.03.012

10.3969/j.issn.1003-7985.2014.03.012

Received 2013-12-11.

Biographies：Chen Dalin (1980—), male, graduate; Chen Nan (corresponding author), male, doctor, professor, nchen@seu.edu.cn.