棒/线两嵌段共聚物共混体系的自组装
韩向刚, 王鹏飞
(内蒙古科技大学 数理与生物工程学院, 内蒙古 包头 014010)
棒/线两嵌段共聚物共混体系的自组装
韩向刚, 王鹏飞
(内蒙古科技大学 数理与生物工程学院, 内蒙古 包头 014010)
运用二维格子自洽场方法, 研究棒/线两嵌段共聚物共混体系的自组装.结果表明: 在长/短两种嵌段体积比相等的棒/线两嵌段共聚物共混体系中, 当某种共聚物的混合比较大时, 观察到层状结构, 层的厚度与混合比大的嵌段共聚物长度有关; 在两种嵌段共聚物混合比相差较小的条件下, 出现了新的自组装结构, 即柱层和层与柱共存相, 这两种结构未出现在棒/线内嵌段共聚物熔体体系中, 它们的出现与棒/线两嵌段共聚物链构象的不对称性及共混的影响有关.
棒/线两嵌段共聚物; 共混体系; 自组装; 自洽场方法
嵌段共聚物具有纳米有序结构, 通过合成两嵌段共聚物或采用不同聚合物混合的方法可控制嵌段共聚物的有序结构.在线/线两嵌段共聚物和某种均聚物的混合系统中, 柔性均聚物的存在改变了嵌段共聚物有序结构的几何性质, 并出现新的稳定有序结构[1].由于棒和线链构象不同, 因此具有刚性链的聚合物与其他聚合物混合对自组装行为的影响较复杂.文献[2-5]通过向棒/线两嵌段和三嵌段共聚物添加构成共聚物的柔性或刚性均聚物, 研究了均聚物添加对自组装结构尺寸和自组装结构相对稳定性的影响; 文献[6]通过实验研究了棒/线两嵌段共聚物与柔性两嵌段共聚物混合物的薄膜体系.现有文献表明, 棒/线两嵌段共聚物与其均聚物混合体系的研究较多, 对其他棒/线嵌段共聚物混合体系中链刚性对混合体系性质的影响研究较少.
自洽场方法是目前最精确的平均场方法[7], 格子自洽场方法采用传递矩阵描述高分子链构象, 利用刚性嵌段的体积排斥效应代替各向异性相互作用, 因此求解自洽场方程组的计算相对简单, 并可处理含有刚性嵌段共聚物的相行为[8-9]及预测新的有序结构.本文利用格子自洽场模型, 研究短/长两种嵌段体积比相等的棒/线两嵌段共聚物共混体系的自组装行为, 并分析棒/线两嵌段共聚物链构象的不对称性及共混对自组装结构的影响.
1 模型体系和理论方法
系统由n条长的棒/线两嵌段共聚物和ns条短的棒/线两嵌段共聚物构成, 假设每条长高分子链由NA个A单体和NB个B单体组成, 高分子链聚合度Ns=NA+NB; 每条短的高分子链由NAs个A单体和NBs个B单体组成, 高分子链聚合度Ns=NAs+NBs, 所有链段尺寸相同, 每个链段占据一个格点, 整个格子均被链段占据.格点总数NL, 因此有NL=nN+nsNs.用传递矩阵λ描述高分子链, 它依赖于所选择的链模型, 采用不直接回头的无规行走链模型, 对于线嵌段A,
对于棒嵌段B,
其中:r′表示r的最近邻点;rj,s和αj,s分别表示第j个高分子链的第s链段的位置和方向;α为由格子模型决定的任何一个键取向;z为所用格子的配位数.
按照Leermakers和Scheutjens的算法[10], 嵌段共聚物的末端分布函数Gαs(r,s|1)服从如下递推关系:
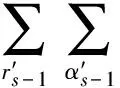
另一个链末端分布函数为
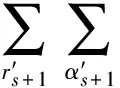
自由能函数表达式为

分别表示长/短嵌段共聚物的单链配分函数.
取自由能函数F的极小值, 可得如下自洽场方程组:
采用两步弛豫方法[8]求解自洽场方程组.求解自洽场方程组步骤为: 先通过随机函数产生初始势场ωA(r)和ωB(r), 再利用方程(3)~(7)求得体积分数和自由能, 并更新化学势场, 通过迭代求解.当相邻两个迭代步骤的自由能之差小于设定的精度时, 系统弛豫停止.比较得到的不同随机势场末态, 自由能最小的为系统稳态.
2 结果与讨论
2.1棒/线两嵌段共聚物熔体的自组装
在模拟计算中, 格子尺寸为40×40的立方格子, 高分子链聚合度N=20, 采用周期性边界条件.在二维正方格子中验证三维简立方格子中棒/线两嵌段共聚物熔体的自组装行为, 如图1所示.由图1可观察到稳定的胶束(图1(A))、柱状(图1(B))和层状相(图1(C))的二维有序结构.当frod=0.2,frod=0.3时, 胶束结构为稳定相; 当frod=0.4时, 柱状结构为稳定相, 未观察到穿孔层结构, 这与三维结果不同.当frod≥0.5时, 层状结构为稳定结构, 以Zigzag层作为亚稳结构(图1(D)), 除未观察到三维螺旋结构外, 二维空间系统的相图与三维结果[8]基本一致.

图1 嵌段共聚物熔体和共混体系的自组装结构Fig.1 Ordered structures observed in rod/coil diblock copolymers and their blends
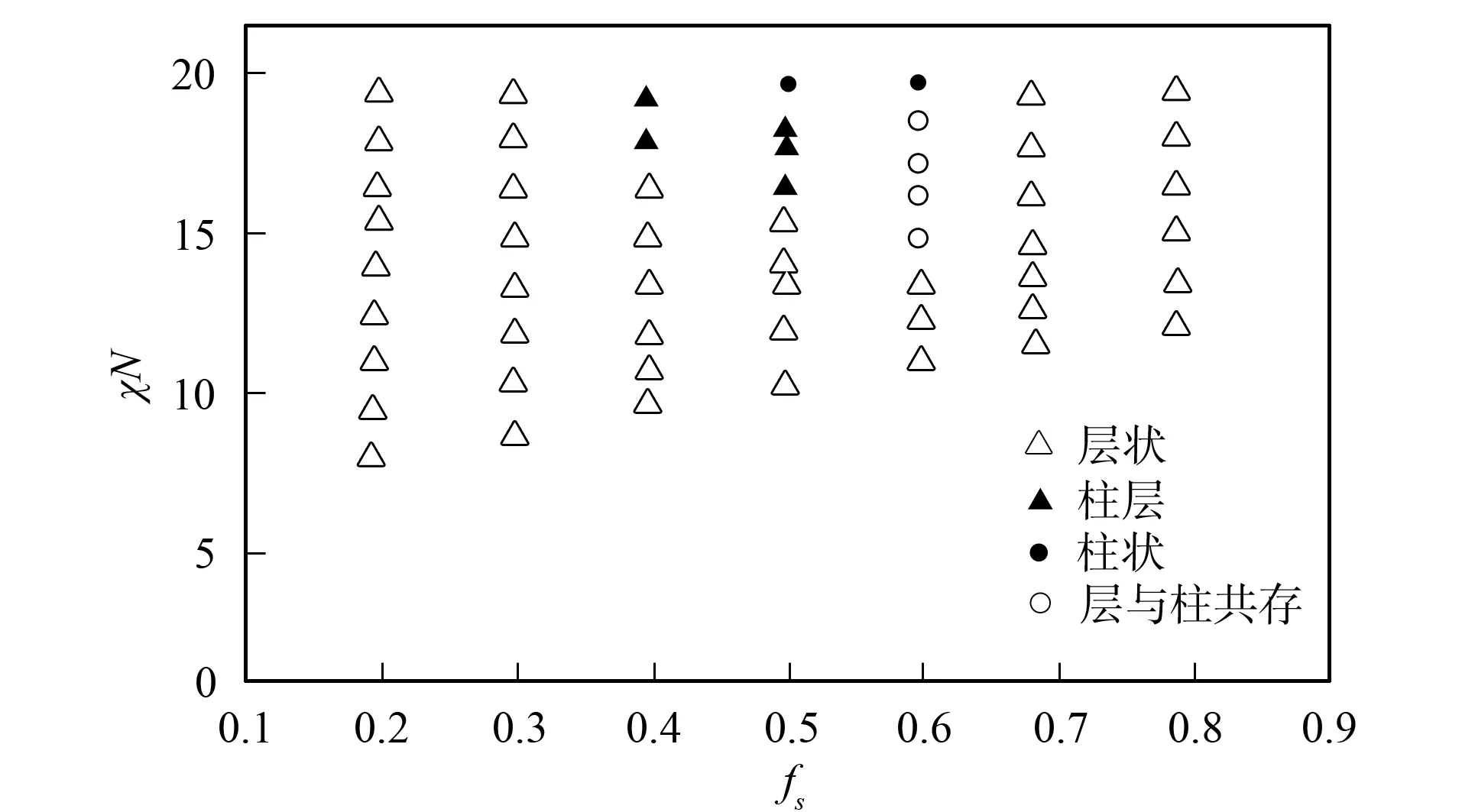
图2 棒/线两嵌段共聚物共混系统相图Fig.2 Phase diagram for the blends of rod/coil diblock copolymer
2.2棒/线两嵌段共聚物共混体系的自组装
模拟短/长两种嵌段比例相等的棒/线两嵌段共聚物的相行为, 构建系统相图, 如图2所示.由图2可见: 当短嵌段共聚物混合比相差较小(fs≤0.3)时, 在弱分凝的条件下(χN≤20), 共混体系自组装为层状结构; 当两种嵌段共聚物混合比相差较大时, 层状结构的厚度与混合比有关; 当长嵌段共聚物的混合比较大时, 层的厚度较大, 当短嵌段共聚物的混合比较大时, 层的厚度较小; 当两种嵌段共聚物混合比相差较小(0.4≤fs≤0.6)时, 系统出现多种自组装结构, 包括柱、柱层和层与柱共存结构; 当fs=0.5时, 柱层出现在比层更大的相分凝程度区域, 这与多嵌段共聚物体系的结果一致[11]; 继续增加相分凝程度, 柱状结构为稳定相, 这与多嵌段共聚物体系出现穿孔层不同, 即柱层相为层和柱的过渡相; 当fs=0.4, 且相分凝增加到一定程度时, 柱状相为稳定相; 当fs=0.6, 且相分凝程度较大时, 柱状相也为稳定相, 但层和柱之间的相不再是柱层相, 而是层和柱的共存相, 这是由于随着短嵌段体积比的增加, 自组装结构需提供更大的界面供短嵌段共聚物占据, 而层/柱共存相的棒/线聚集区之间的界面比柱层相更大所致.在对应的柔性两嵌段共聚物共混体系中, 两种嵌段共聚物混合比相差较小也出现层和柱的共存结构, 与上述结果一致[12].
综上所述, 本文利用格子自洽场方法, 在正方格子中计算了弱分凝条件下棒/线两嵌段共聚物熔体和其共混体系的相行为.结果表明: 在二维空间观察到了胶束、条状和层状3种稳定结构, 并得到了与三维空间基本一致的系统相图; 在长/短两种嵌段体积比相等的棒/线两嵌段共聚物共混体系中, 当两种嵌段共聚物混合比相差较小时, 出现新的自组装结构, 有柱层和层与柱共存相, 这两种相未在棒/线两嵌段共聚物的熔体体系中出现, 这是由于两种棒/线嵌段共聚物链构象不对称所致.
[1]Matsen M W.Phase-Behavior of Block Copolymer/Homopolymer Blends [J].Macromolecules, 1995, 28(17): 5765-5773.
[2]He L L, Zhang L X, Chen H P, et al.Effect of Nanorods on the Meseophase Structure of Diblock Copolyners [J].J Chem Phys, 2009, 130: 144907.
[3]Tao Y F, Olsen B D, Ganesan V, et al.Domain Size Control in Self-assembling Rod-Coil Block Copolymer and Homopolymers Blends [J].Macromolecules, 2007, 40(9): 3320-3327.
[4]Gao L C, Yao J H, Shen Z, et al.Self-assembly of Rod-Coil-Rod Triblock Copolymer and Homopolymer Blends [J].Macromolecules, 2009, 42(4): 1047-1050.
[5]SONG Wendi, TANG Ping, QIU Feng, et al.Phase Behavior of Rod-Coil Diblock Copolymer and Homopolymer Blends from Self-consistent Field Theory [J].J Phys Chem B, 2011, 115(26): 8390-8400.
[6]SHI Lingying, ZHOU Yu, SHEN Zhihao, et al.Hierarchical Structures in Thin Films of Macrophase- and Microphase-Separated AB/AC Diblock Copolymer Blends [J].Macromolecules, 2012, 45(13): 5530-5537.
[7]Matsen M W, Schick M.Stable and Unstable Phases of a Diblock Copolymer Melt [J].Phys Rev Lett, 1993, 72(16): 2660-2663.
[8]CHEN Zhizhong.A Novel Self-consistent-field Lattice Model for Block Copolymers [J].J Chem Phys, 2006, 124(10): 104907-104911.
[9]韩向刚, 张程祥.棒/棒二嵌段共聚物自组装行为的自洽场研究 [J].高等学校化学学报, 2010, 31(3): 566-570.(HAN Xianggang, ZHANG Chengxiang.Study on Self-assemble of Rod-Rod Diblock Copolymers with Self-consistent Field Lattice Model [J].Chemical Journal of Chinese Universities, 2010, 31(3): 566-570.)
[10]Leermakers F A M, Scheutjens J M H M.Statistical Thermodynamics of Association Colloids.Ⅰ.Lipid Bilayer Membranes [J].J Chem Phys, 1988, 89(5): 3264-3274.
[11]XIA Yingdong, CHEN Jizhong, SHI Tongfei, et al.Self-assembly of Linear Rod-Coil Multiblock Copolymers [J].Chinese Journal of Polymer Science, 2013, 31(9): 1242-1249.
[12]Wu Z Q, Li B H, Jin Q H, et al.Phase Behavior of Binary Blends of Diblock Copolymers [J].J Phys Chem B, 2010, 114(48): 15789-15798.
Self-assemblyoftheBlendsofRod/CoilDiblockCopolymers
HAN Xianggang, WANG Pengfei
(SchoolofMathematics,PhysicsandBiologicalEngineering,InnerMongoliaUniversityofScienceandTechnology,Baotou014010,InnerMongoliaAutonomousRegion,China)
Based on the self-consistent field theory of lattice model in two dimension space, the self-assembly of the blends of diblock copolymers was studied.For the blends of long/small two diblock copolymers in which volume fraction of rod block equal that of coil block, when blend fraction of the two diblocks was not comparable, lamellae were observed, and their thickness was related with the length of the big blend fraction of the two diblock copolymers; on the other hand, as blend fraction of the two diblocks is comparable, the new ordered structures, including lamellar strips and coexisted lamellae and strips, were observed.These new ordered structures did not appear in the rod/coil diblock copolymer melts.The results are related to the asymmetry of the chain conformation and the blend of rod/coil diblock copolymer.
rod/coil diblock copolymer; blends; self-assembly; self-consistent field theory
2014-04-18.
韩向刚(1979—), 男, 锡伯族, 博士, 从事软凝聚态物理的研究, E-mail: xghan0@163.com.
国家自然科学基金(批准号: 11147132)和内蒙古自治区自然科学基金(批准号: 2012MS0112).
O411
A
1671-5489(2014)06-1297-04
10.13413/j.cnki.jdxblxb.2014.06.36
王 健)

