基于分量替换高分辨率遥感图像融合方法的对比研究

李春华

（福建师范大学 地理科学学院，福州350007）

Aiazzi等［1］在对25a来遥感图像融合的回顾中最新提出了遥感图像融合可以分为两类方法：分量替换法和多分辨率分析法。分量替换融合方法是其中一类重要的融合方法，该方法基于新的向量空间对原始的多光谱图像进行光谱变化。分量替换融合思想最早出现在Carper等［2］提出的IHS融合方法中。该方法首先对多光谱数据（仅限3个波段）进行IHS变换，再用Pan波段数据替换I分量，最后将新的数据集进行IHS逆变换即可获得融合图像。通常在进行波段替换之前，将Pan波段进行直方图匹配，使得Pan波段总体的均值与方差和I分量一致。随后出现的主成分融合法（PCA）和IHS融合法相似，区别在于PCA融合法是利用Pan波段数据替换第一主成分（PC1），并可以对多个波段进行融合处理［3］。

由 Laben 和 Brover［4］提 出 的 Gram－Schmidt（GS）融合算法是另一个基于分量替换思想的融合算法。该方法首先模拟低分辨率全色波段，将模拟的低分辨率全色波段作为第一分量参与GS正交变换，再将Pan波段替换第一分量构成新的数据集进行GS逆变换得到融合图像。在进行波段替换之前，将Pan波段进行直方图匹配，使得Pan波段总体的均值与方差和模拟的低分辨率全色波段一致。

以上提到的IHS，PCA和GS分量替换法的基本方法都是在进行逆变换之前，将Pan波段替换经变换后的第一分量（称为可替换分量），在替换前首先对Pan波段进行直方图匹配，使得Pan波段总体的均值、方差和所替换的分量一致，但是由于局部均值和方差的不一致往往导致融合图像出现光谱失真。为了改善光谱失真，Aiazzi等［5］提出了改进的分量替换法，该方法首先通过对全色波段和多光谱波段进行线性回归获取拟合系数来构造可替换分量，再将Pan波段替代可替换分量进行逆变换获取融合图像，改进的分量替换法可以应用在IHS和GS融合算法中。分量替换法由于其简单快速的特点，在高分辨率遥感图像融合中一直得以运用，但涉及该方法关键性原理的阐述在国内还鲜有报道，在众多的应用中往往由于缺乏对该融合算法机理的理解而未能得以正确使用。

为此，本文首先从线性代数的角度阐述分量替换融合算法的实质，并对基于光谱响应函数模拟低分辨率全色波段和基于多元线性回归模拟低分辨率全色波段的这两种GS融合算法进行原理分析。其次，以QuickBird数据为例，进行三种基于分量替换的融合方法的对比分析，分别是PCA融合法、基于光谱响应函数模拟低分辨率全色波段的GS融合法［6］、基于多元一次线性回归拟合低分辨率全色波段的GS融合法［5］。最后，对上述三种融合算法的光谱保真性进行评价，并分析融合影像光谱失真的原因，以此来探明高分辨率遥感图像融合的研究方向。

1 原理分析

1.1 分量替换融合算法的实质

Dou等［7］分析了分量替换融合方法的理论框架，本研究从线性代数的角度结合Dou的理论框架更为具体地阐述分量替换融合算法的技术细节和实质。

首先，假设原多光谱数据有n个波段，将多光谱数据用矩阵形式表示为：

式中：MSi（i＝1，2，…，n）——用行向量的形式表示的原始多光谱波段数据。

将多光谱波段数据进行线性变换（只须可逆变换即可）得到新的数据集，表示为：

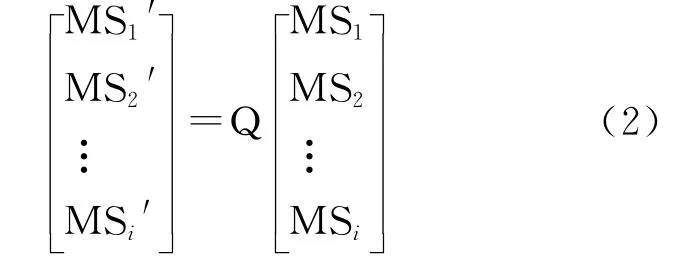
式中：MSi′（i＝1，2，…，n）——经过线性变换后的各多光谱波段数据；Q——线性变换对应的可逆矩阵。

用全色波段Pan替换MS1′得到新的数据集，对新数据集进行逆变换，得到融合影像，见式（3）：

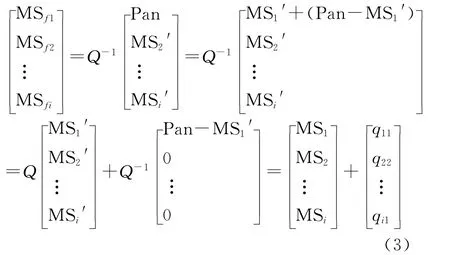
式中：MSfi（i＝1，2，…，n）——融合后的各多光谱波段数据；qi1（i＝1，2，…，n）——Q－1的第一列向量的各分量元素。以上的推理过程说明，任意的非退化矩阵（可逆矩阵）都可以定义相应的线性变换，式（3）表明融合的结果实质上是由两部分构成，一部分是原始的多光谱图像，另一部分Pan－MS1′代表Pan波段数据的高频部分。融合的效果取决于线性变换的第一分量MS1′，MS1′称为被替换波段，在IHS融合算法中MS1′即为I分量，PCA融合算法中MS1′表示第一主成份PC1，在GS融合算法中 MS1′称为模拟的低分辨率全色波段。

因此，减少光谱失真的关键性技术就在于构造被替换的波段 MS1′。只有当 MS1′能真实地模拟出Pan波段的灰度信息，Pan－MS1′才能确切地反映出Pan波段数据的高频信息，否则其中必然包含不一致的灰度信息，从而造成融合影像光谱失真。

1.2 两种典型的构造可替换波段的分量替换法

基于光谱响应函数模拟低分辨率全色波段的GS融合算法［6］和基于多元线性回归方法模拟低分辨率全色波段的GS融合算法［5］是两种十分有代表性的通过构造可替换波段改进光谱失真的分量替换方法，以下对这两种方法的原理进行说明。

1.2.1 基于光谱响应函数模拟低分辨率全色波段的GS融合算法 理解光谱响应函数对传感器接收到的辐射亮度值的影响是说明基于光谱响应函数模拟低分辨率全色波段的GS融合算法的前提，因此，本节首先说明什么是光谱响应函数以及光谱响应函数对影像融合的影响，再解释该融合算法的具体步骤。光谱响应函数反映的是传感器的一种静态性能，遥感器的光谱响应特征是波长的函数，是遥感器在每个波长处接收辐亮度与入射辐亮度的比值。不同传感器光谱响应函数曲线的形状、波段中心波长位置、带宽、波段之间交迭程度等的不同都将导致它们观测得到的波段反射率不一致［8］。遥感器每个波段都有一定的波长响应宽度，遥感器的每个波段实际接收到的能量是该波段的波长范围内各个波长处接收的能量的和。通常采用对遥感器接受的辐亮度按照光谱响应函数进行归一化来降低光谱响应特征不同的影响［8］，如（4）式所示。

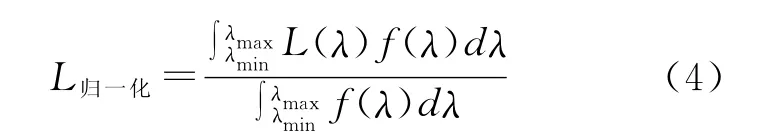
式中：f（λ）——遥感器某波段的光谱响应函数；L（λ）——入射到遥感传感器所接收到并记录的辐亮度值；λmax，λmin——波段范围的上下界。

为了说明光谱响应函数对遥感图像融合的影响，本文以QuickBird数据为例，表1表示QuickBird各波段波长范围和中心波长，图1表示QuickBird的光谱响应特征［9］，从表1和图1可以看出Blue、Green、Red和NIR各波段之间都有交迭，而且Pan波段上界超出了NIR的上界，全色波段与多光谱波段光谱响应函数不完全一致。如果按照传统的GS融合方法，仅仅通过简单地选取多光谱图像的均值来模拟低分辨率全色波段，该方法虽然快速简单，但不能准确获取Pan波段数据在低分辨率情况下的灰度信息。

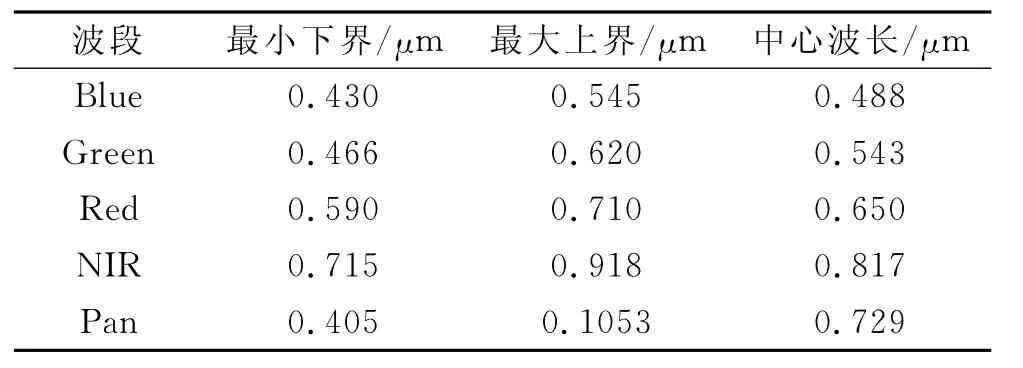
表1 QuickBird波段范围和中心波长［9］

为了避免上述问题，Gonzales［6］通过对 MS与Pan传感器的光谱响应函数进行线性回归，获取使用MS模拟低分辨率Pan的线性组合系数，再将模拟的低分辨率全色波段应用到GS融合模型中。具体步骤如下：

（1）首先对MS和Pan的光谱响应函数进行线性回归，获取各波段的拟合系数 ，通过对MS各波段的光谱响应函数的线性组合模拟Pan波段的光谱响应函数，见式（5）：

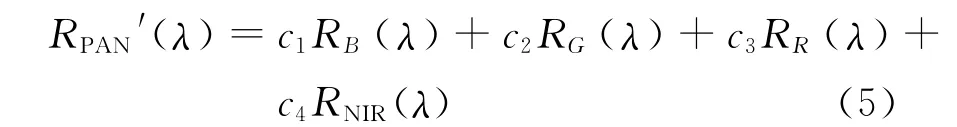
其中：RPAN′（λ）为模型的Pan波段的光谱响应函数，RB，RG，RR，RNIR分别为红、绿、蓝、近红外波段的光谱响应函数。

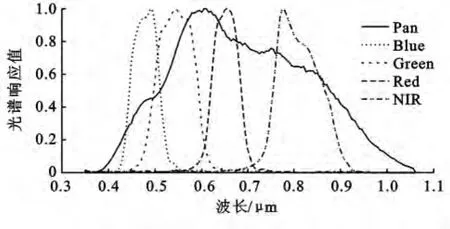
图1 QuickBird多光谱波段和全色波段的光谱响应函数［9］

（2）由于模拟Pan波段光谱响应函数和Pan波段很接近，因此由模拟的Pan波段光谱响应函数所记录的光谱辐射值与Pan波段数据具有较高的可比性，这一模拟的低分辨率全色波段辐射亮度值可以表示为

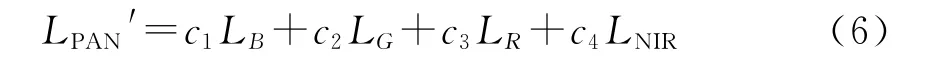
式中：LPAN′（λ）——模拟的Pan波段的辐射亮度值；LB，LG，LR，LNIR——红、绿、蓝、近红外波段的辐射亮度值；ci（i＝1，2，3，4）——拟合系数。

（3）最后，将模拟的低分辨率Pan波段数据应用到GS融合模型中。

1.2.2 基于多元线性回归方法模拟低分辨率全色波段的GS融合算法 Aiazzi等［5］在研究改进的分量替换方法中利用最小二乘法，直接通过全色波段和多光谱波段进行线性回归获取拟合系数来模拟出低分辨率全色波段。算法的具体步骤如下：

（1）将原始Pan波段数据通过低通滤波重采样为分辨率和原始多光谱波段分辨率一致的图像，记为P。假设

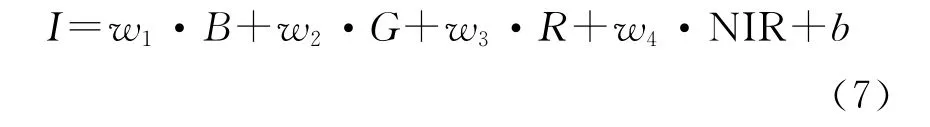
式中：I——所要模拟的低分辨率全色波段I的估计量，通过线性回归方法最小化P和I之间的PMSE获取估计量w1，w2，w3，w4和b。

（2）通过以上的拟合系数模拟出低分辨率全色波段

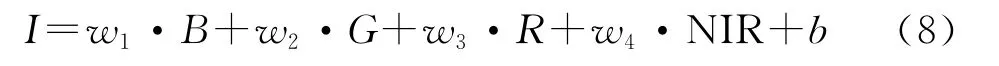
（3）最后，将模拟的低分辨率全色波段数据应用到GS融合模型中。

2 融合实验结果与分析

为了进一步理解分量替换融合思想，并检验改进的分量替换融合方法在光谱保真性上的改善。本文进行三种典型的分量替换融合方法的对比分析，分别是PCA融合法、基于光谱响应函数模拟低分辨率全色波段的GS融合法（以下简称GS1）以及基于多元一次线性回归拟合低分辨率全色波段GS融合法（以下简称GS2）。

2.1 数据说明

遥感数据融合前的辐射水准归一化以及参与融合的各波段数据的精确配准是融合前的重要基础工作。论文所选取的数据为DigitalGlobe公司的Demo数据（qb＿boulder＿msi和qb＿boulder＿Pan），多光谱图像大小为1 024×1 024像素，多光谱图像空间分辨率为2.8m，全色图像空间分辨率为0.7m。图像的辐射分辨率为11bit，以16bit的格式发放，数据的动态范围为0～2 047。影像级别为标准产品（Standard Imagery Products）：具有地理参考和地图投影，经过了辐射校正、传感器和卫星平台引起的系统误差校正，利用粗DEM做了地形误差校正，经过了全色和多光谱波段之间的配准。由于所选取的数据已经经过了辐射校正和各波段间的配准，可直接用于本文的融合实验。

本文选取ENVI 5.0软件实现PCA和GS融合实验。目前集成在ENVI 5.0软件中的GS算法有4种可选择的模式用来模拟低分辨率全色波段，模式一：选取多光谱波段的均值来模拟低分辨率全色波段；模式二：输入现有的单波段数据来模拟低分辨率全色波段；模式三：基于不同传感器光谱响应函数模拟低分辨率全色波段；模式四：自定义低通滤波函数来模拟低分辨率全色波段。本实验选择模式三进行GS1融合实验，选择模式四进行GS2融合实验。

2.2 融合效果对比

融合效果评价是一个复杂的问题，均值差（Mean Bias，MB）、方差差异（Variance Difference，VD）、标准偏差差异（Standard Deviation Difference，SDD）、相 关 系 数 （Correlation Coefficient，CC）、光 谱 角（Spectral Angle Mapper，SAM）、相对量纲全局误差（Relative Dimensionless Global Error，ERGAS）、Q4质量评价指标（Q4Quality Index，Q4）是目前遥感领域常用的7个融合质量评价指［10－13］。Zhang［14］通过比较实验发现这7个指标的定量评价结果和目视比较分析结果以及数字分类结果存在严重的不一致，他认为目前国际上常用上述7个指标并不能作为评价遥感图像融合质量的可靠标准。

因此本研究没有使用7个评价指标，而是从融合前后图像的总体和细节（典型地物）的光谱特征展开比较：（1）从总体上进行比较，包括融合影像与原始影像的相关系数、RMSE和灰度直方图的比较；（2）融合影像与原始影像典型地物的光谱特性比较，所选取的典型地物既有高反射率地物（如沙地、水泥地），也有低反射率地物（如水体），还包括植被。依此来考察经过融合处理后的影像在整个谱段范围的光谱保真性。

2.2.1 融合影像与原始影像的总体比较 从融合目视效果看，三种方法融合处理后的影像都纹理清晰，地物清晰可辨，PCA和GS2融合影像颜色上和原多光谱图像非常一致，但GS1融合后影像上植被的颜色明显比原多光谱图像亮。下文从融合影像与原始影像的灰度直方图、相关系数和RMSE三方面来做比较分析。（1）图2显示，从总体上，三种方法融合后的图像和原多光谱图像各波段的灰度直方图较为一致，并且各融合图像之间各波段的灰度直方图极其一致，几乎重叠在一起。（2）从所获取的相关系数（表2）来看，相关系数都接近1，其中GS2融合后Band1，Band2，Band3和原多光谱图像的相关系数最高（0.917 1，0.919 8，0.921 4），PCA融合后Band4和原多光谱图像的相关系数最高（0.931 0）。（3）表3中所有RMSE≤2.5%灰度范围，其中PCA融合后的Band1、Band2和原多光谱图像的RMSE最小（10.906 0，22.321 3），GS2融合后的 Band3、Band4和原多光谱图像的RMSE最小（28.572 7，46.876 8）。

从总体的比较分析发现，三种融合方法都具有很高的光谱保真性，其中GS2具有最优的光谱保真性，PCA和GS1融合算法次之。

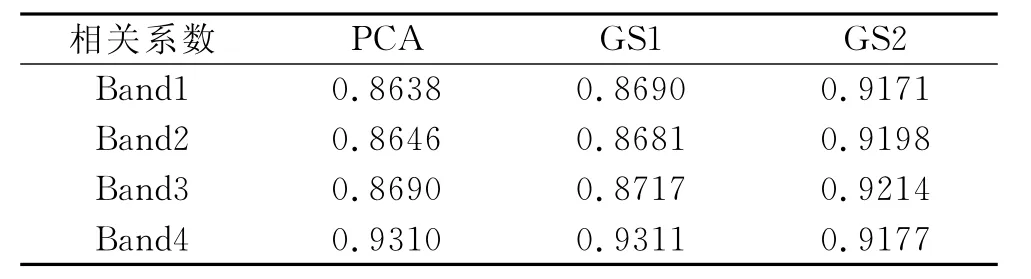
表2 融合影像与原始影像的相关系数

表3 融合影像与原始影像的RMSE

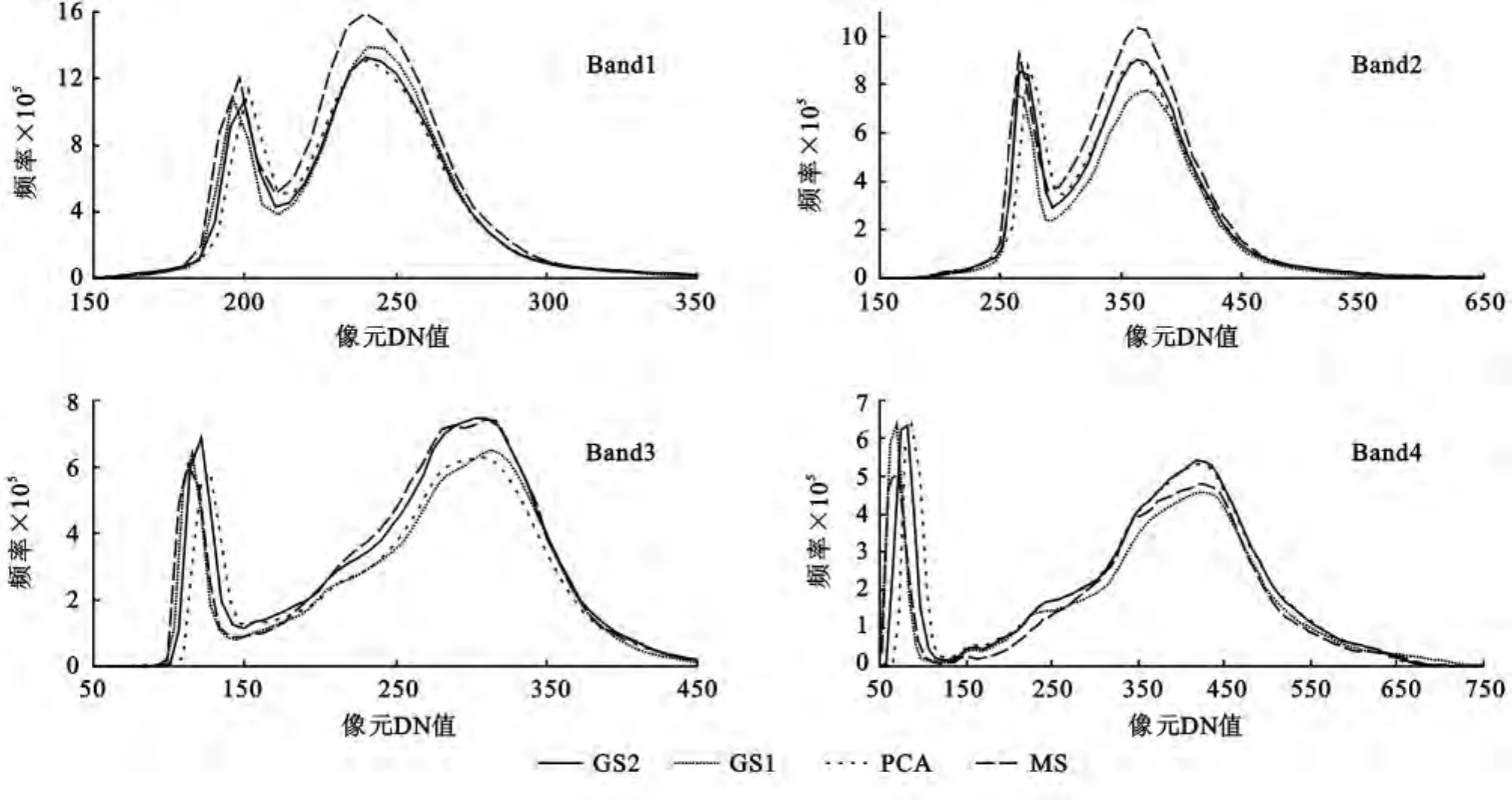
图2 原始图像和融合后图像的灰度直方图

2.2.2 融合影像与原始影像典型地物的光谱特性比较 为了进一步更全面考察经过融合处理后影像的光谱保持性，本研究选取纯净的水体（代表低反射率地物）、植被和建筑（代表高反射率地物）三种典型地物来探究融合前后影像光谱特性的变化。尽量选取同质均匀的典型地物区域，以利于融合前后典型地物光谱特性的对比。

（1）PCA、GS1、GS2融合前后水体的光谱特性比较。根据水体的光谱反射率随着波长的增大逐渐降低的特性，本研究选取水体的绿光波段（Green）和近红外波段（NIR）进行光谱分析，图3表示融合前后水体在Green和NIR波段水平方向的光谱剖面曲线，分析图3可以得出以下结论：① 经过PCA融合处理后图像水体的Green和NIR波段灰度值略高于原图像；② 经过GS1、GS2融合后的图像和原始图像水体的Green波段灰度值几乎完全一致；③ 经过GS1融合后的图像水体的NIR波段灰度值和融合前最为接近。因此，GS1融合方法具有最优的水体光谱保真性，GS2次之，PCA融合方法在水体的绿光和近红外波段的光谱反射率略高于原图像。

（2）PCA、GS1、GS2融合前后植被的光谱特性比较。根据植被在红光（Red）吸收而在近红外（NIR）波段反射剧增的光谱特性，论文中选取Red和NIR波段进行植被的光谱分析，图4表示融合前后植被在Red和NIR波段的空间光谱剖面曲线（利用ENVI软件绘制图像的线向量的空间光谱剖面曲线），分析融合前后Red和NIR的变化可以得出以下结论：①经过GS1融合处理后的图像植被的Red和NIR波段明显高于原图像和其他融合结果，这一结论和Konstantinos［15］的结论相一致，Konstantinos认为融合后植被覆盖地区能够更容易从耕地和建筑物中区分出来；②GS2融合处理后的图像植被的Red和NIR波段和原图像最接近，PCA融合方法次之。

（3）PCA，GS1，GS2融合前后建筑物的光谱特性比较。选取Green和NIR波段进行建筑物的光谱分析，图5为融合前后建筑在Green和NIR波段的空间光谱剖面曲线（利用ENVI软件绘制图像的线向量的空间光谱剖面曲线），经过分析有如下结论：① 经过GS1融合处理后的图像建筑物在Green和NIR波段的灰度值都明显低于原图像；② 经过PCA和GS2融合处理后的图像建筑物在Green波段和NIR波段灰度值略低原图像，其中PCA融合结果和原图像最为接近。

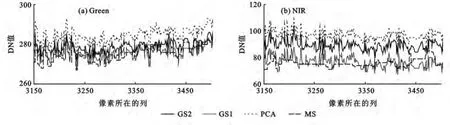
图3 融合前后水体在Green和NIR波段水平方向的光谱剖面曲线

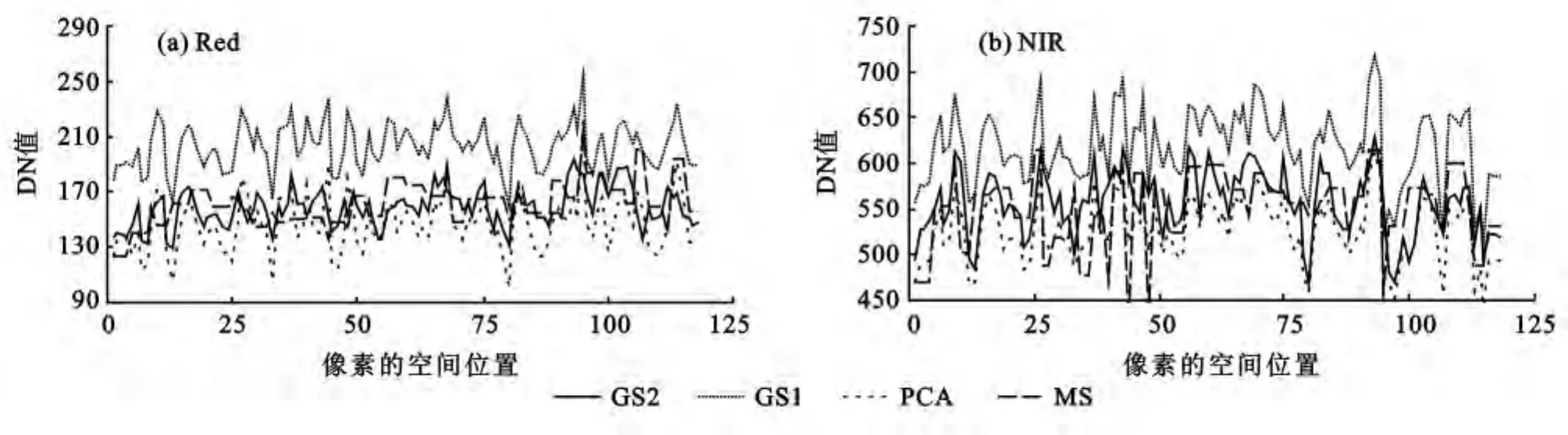
图4 融合前后植被在Red和NIR波段的空间光谱剖面曲线

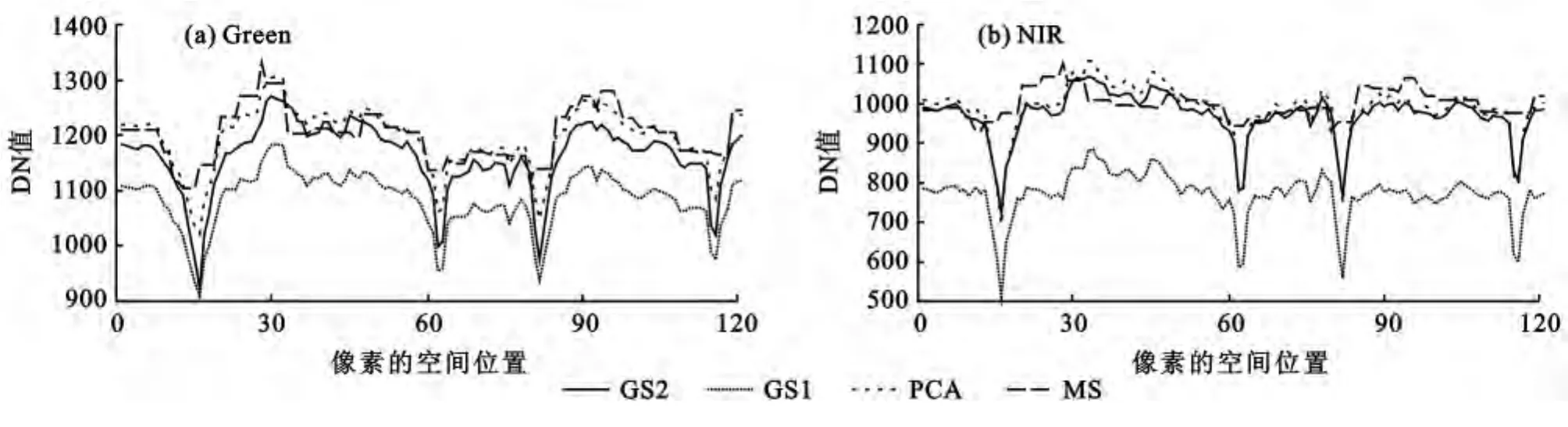
图5 融合前后建筑在Green和NIR波段的空间光谱剖面曲线

3 结论

（1）从总体的比较（融合影像与原始影像的相关系数、RMSE和灰度直方图）和典型地物在融合前后的光谱保持性的比较一致发现，三种融合方法都具有很高的光谱保真性，其中基于多元一次线性回归拟合低分辨率全色波段的GS2融合方法具有最优的光谱保真性，PCA和GS1融合方法次之。尤其值得注意的是GS1融合处理后的图像存在部分光谱失真的现象。经过GS1融合处理后的图像，植被覆盖地区Red和NIR波段光谱反射率明显高于原始的多光谱图像，而高反射率区域（如沙地、水泥建筑）Green和NIR波段光谱反射率则明显低于原始的多光谱图像。

（2）造成GS2融合算法明显优于GS1的原因是GS1融合算法使用的只是实验室理想环境下所获取的名义上的光谱响应特征。传感器的实际成像过程受到诸多因素的影响，如传感器在轨工作环境、大气的影响、观测角度不同等的影响。GS1算法单纯通过不同波段的光谱响应函数的线性组合来模拟低分辨率全色波段并不十分准确，GS2直接利用MS和Pan波段像元灰度值进行线性回归，克服了上述不确定性问题。

（3）通过对PCA、GS1和GS2三种融合算法的光谱保真性的比较分析说明，如何利用多光谱数据准确地模拟低分辨率全色波段，直接影响到融合后影像的光谱保真性，是目前高分辨率遥感图像融合的关键技术。由多光谱数据模拟低分辨率全色波段的方法引起了越来越多研究人员的重视，也代表了目前高分辨率遥感图像融合的研究方向。

［1］ Aiazzi B，Alparone L，Baronti S，et al.25years of pansharpening：a Critical Review and New Developments［M］∥Signal and Image Processing for Remote Sensing.2nd E－dition.Boca Raton，FL：CRC Press，2011：533－548.

［2］ Carper W，Lillesand T，Kiefer R.The use of intensityhue－saturation transformations for merging SPOT panchromatic and multispectral image data［J］.Photogrammetic Engineering and Remote Sensing，1990，56（4）：459－467.

［3］ Chavez P S，Sides J S C，Anderson J A.Comparison of three different methods to merge multiresolution and mutispectral data：Landsat TM and SPOT panchromatic［J］.Photogrammetic Engineering and Remote Sensing，1991，57（3）：295－303.

［4］ Lanben C A，Brower B V.Process for enhancing the spatial resolution of multispectral imagery using Pansharpening［P］.Tech.Rep.，Eastman Kodak Company：US，6011875.2000.

［5］ Aiazzi B，Baronti S，Selva M.Improving component substitution pansharpening through multivariate regression of MS＋Pan data［J］.Geoscience and Remote Sensing，IEEE Transactions on，2007，45（10）：3230－3239.

［6］ González－Audícana M，Otazu X，Fors O，et al.A low computational－cost method to fuse IKONOS images using the spectral response function of its sensors［J］.Geoscience and Remote Sensing，IEEE Transactions on，2006，44（6）：1683－1691.

［7］ Dou W，Chen Y，Li X，et al.A general framework for component substitution image fusion：An implementation using the fast image fusion method［J］.Computers＆ Geosciences，2007，33（2）：219－228.

［8］ 梁顺林.定量遥感［M］.北京：科学出版社，2009：157－176.

［9］ DigitalGlobe，Inc.Spectral Response for DigitalGlobe Earth Imaging Instruments［EB／OL］.2011.http：∥www.digitalglobe.com／downloads／DigitalGlobe＿Spectral＿Response.pdf.

［10］ Wald L，Ranchin T，Mangolini M.Fusion of satellite images of different spatial resolutions：assessing the quality of resulting images［J］.Photogrammetric Engineering ＆ Remote Sensing，1997，63（6）：691－699.

［11］ Wang Z，Ziou D，Armenakis C，et al.A comparative analysis of image fusion methods［J］.Geoscience and Remote Sensing，IEEE Transactions on，2005，43（6）：1391－1402.

［12］ Wang Z，Bovik A C，Sheikh H R，et al.Image quality assessment：From error visibility to structural similarity［J］.Image Processing，IEEE Transactions on，2004，13（4）：600－612.

［13］ Wang Z，Bovik A C.A universal image quality index［J］.Signal Processing Letters，IEEE，2002，9（3）：81－84.

［14］ Zhang Y.Methods for image fusion quality assessment－a review，comparison and analysis［J］.The International Archives of the Photogrammetry，Remote Sensing and Spatial Information Sciences，2008，37：1101－1109.

［15］ Nikolakopoulos K G.Spatial resolution enhancement of Hyperion hyperspectral data［C］∥Hyperspectral Image and Signal Processing：Evolution in Remote Sensing，2009.WHISPERS′09.First Workshop on.IEEE，2009：1－4.