一种准零刚度隔振器的特性分析与实验研究

徐道临，张月英，周加喜，张 敬

(湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082)

近年来，很多学者通过正负刚度组合提出了具有QZS特性的隔振系统。在小幅振动下，这种系统具有高静刚度低动刚度的特性，从而保证系统在小变形下固有频率很小。最典型的代表是，Carrella等[1-9]将三个线性或非线性弹簧进行组合通过参数优化设计得到一种QZS系统，并进行了一系列的静态和动态分析。Platus[10]利用在轴向载荷作用下表现负刚度特性的纵向弯曲梁和线性弹簧，设计出一种QZS结构。Robertson等[11]运用高静刚度低动刚度理念，利用磁铁弹簧实现了低频隔振。Zhou等[12]通过并联一个磁铁弹簧与一个机械弹簧设计出一个高静刚度低动刚度的半主动隔振系统。刘兴天等[13]讨论了滑动梁与线形弹簧组成的QZS系统带来的新特性。

现有的研究工作主要是关于QZS系统的运动机理和理论分析的，很少有文献涉及这方面的实验研究。为了评估其实际隔振性能，本文利用5个线性弹簧设计了一个简单的QZS模型，并进行了一系列的实验研究。首先，对所建模型进行理论分析，展示其静动力学特性。然后通过实验研究，比较QZS模型与其相应的线性系统在谐波激励作用下的实际隔振性能，评估其实际隔振效果。实验结果表明，QZS系统具有良好的隔振性能，尤其是在低频带，其隔振效果相当显著。

1 数学模型

本文所设计的QZS系统模型包括一个竖直弹簧和四个倾斜弹簧，其中，倾斜弹簧提供的负刚度抵消竖直弹簧提供的正刚度，其结构示意图如图1(a)(不考虑被隔振设备)所示。倾斜弹簧的一端与刚度为kv的竖直弹簧在E点连接，另一端分别铰接在水平面上的A，B,C和D点，且四个倾斜弹簧具有相同的原长L0、刚度k0以及初始水平倾斜角θ0。假设力f作用在点E，方向向下。作用点E的初始位置在水平面ABCD的正上方h处，分别与点A，B,C和D水平相距a。当一个大小合适的质量块置于系统上时，弹簧连接点E会被压缩至平衡点O，此时，倾斜弹簧处于水平状态，静载完全由竖直弹簧支撑，系统演变为QZS系统。位置O是系统的静平衡位置，在位置O附近系统具有高静态刚度低动态刚度，所以研究系统在位置O附近的运动是非常有意义的。

根据系统的结构示意图，建立其在静载作用下处于平衡位置的实验装置模型图，如图1(b)所示。四个支柱被固定在支撑板上，倾斜弹簧的一端与支柱铰接，另一端与导杆铰接。导杆由竖直弹簧支撑，可以在支撑板上的孔中自由滑动。承载平台固定在导杆的顶端，用于安装被隔振质量。为了避免弹簧被压缩时弯曲失稳以及由于各部件间的摩擦而导致系统过阻尼，每个弹簧都设有导杆和直线轴承。

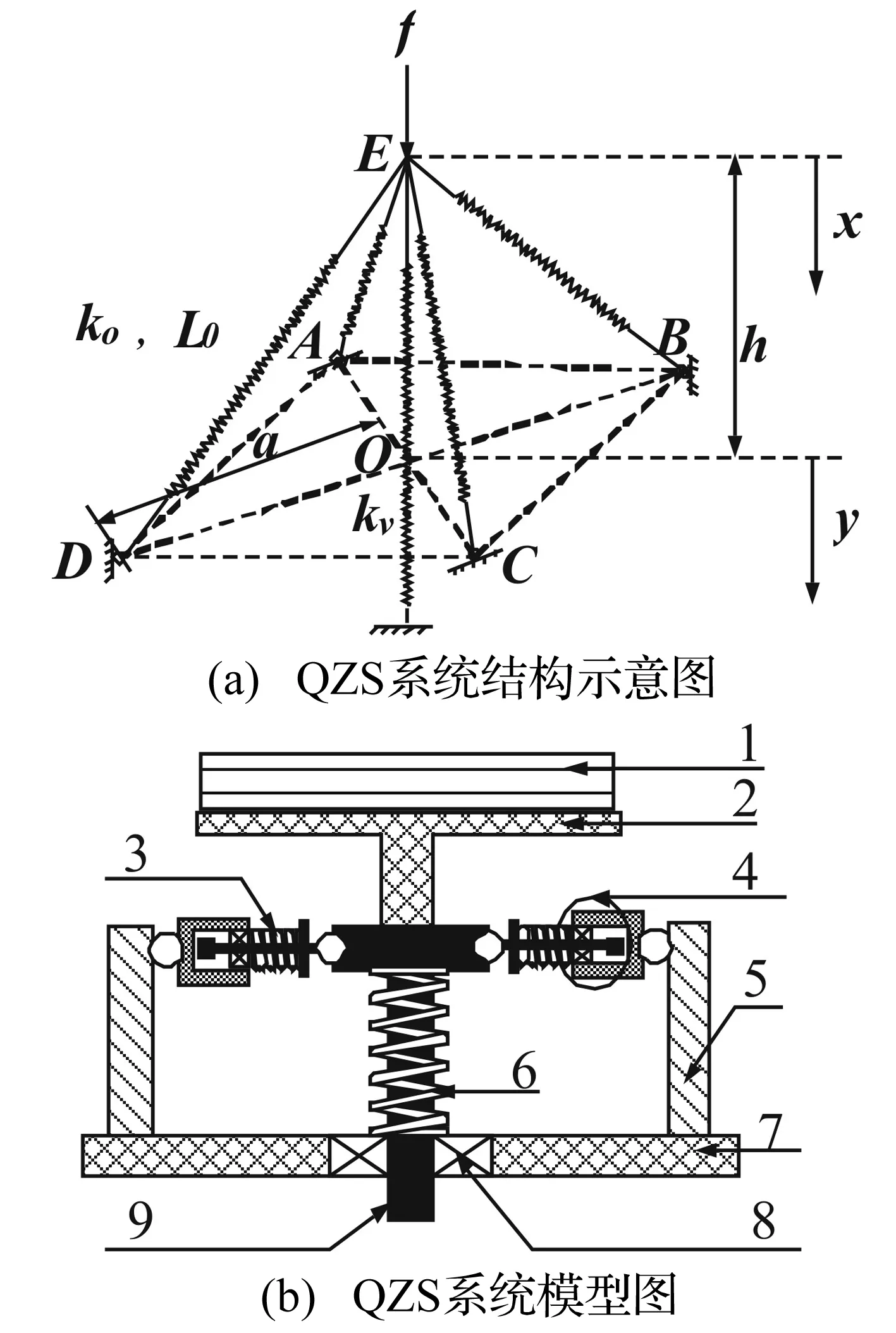
1.静载 2.承载平台 3.倾斜弹簧 4.导向装置 5.支柱 6.竖直弹簧 7.支撑板 8.线性轴承 9.导杆

1.1 组合刚度分析

为了减小设计难度，模型所用弹簧都是线性的。由于倾斜放置的弹簧使系统具有几何非线性，所以图1所示的QZS模型是个非线性系统，其非线性由几何参数a和h决定。假设坐标x定义为点E从初始位置开始在竖直方向上的位移，那么如图1(a)所示，系统在外力f作用下产生位移x，二者的关系可表示为

(1)

如果坐标y定义为点E从位置x=h也就是静平衡位置开始在竖直方向上的位移，那么，式(1)可以表示为

(2)

将力与位移的关系式(2)无量纲化为

(3)

(4)

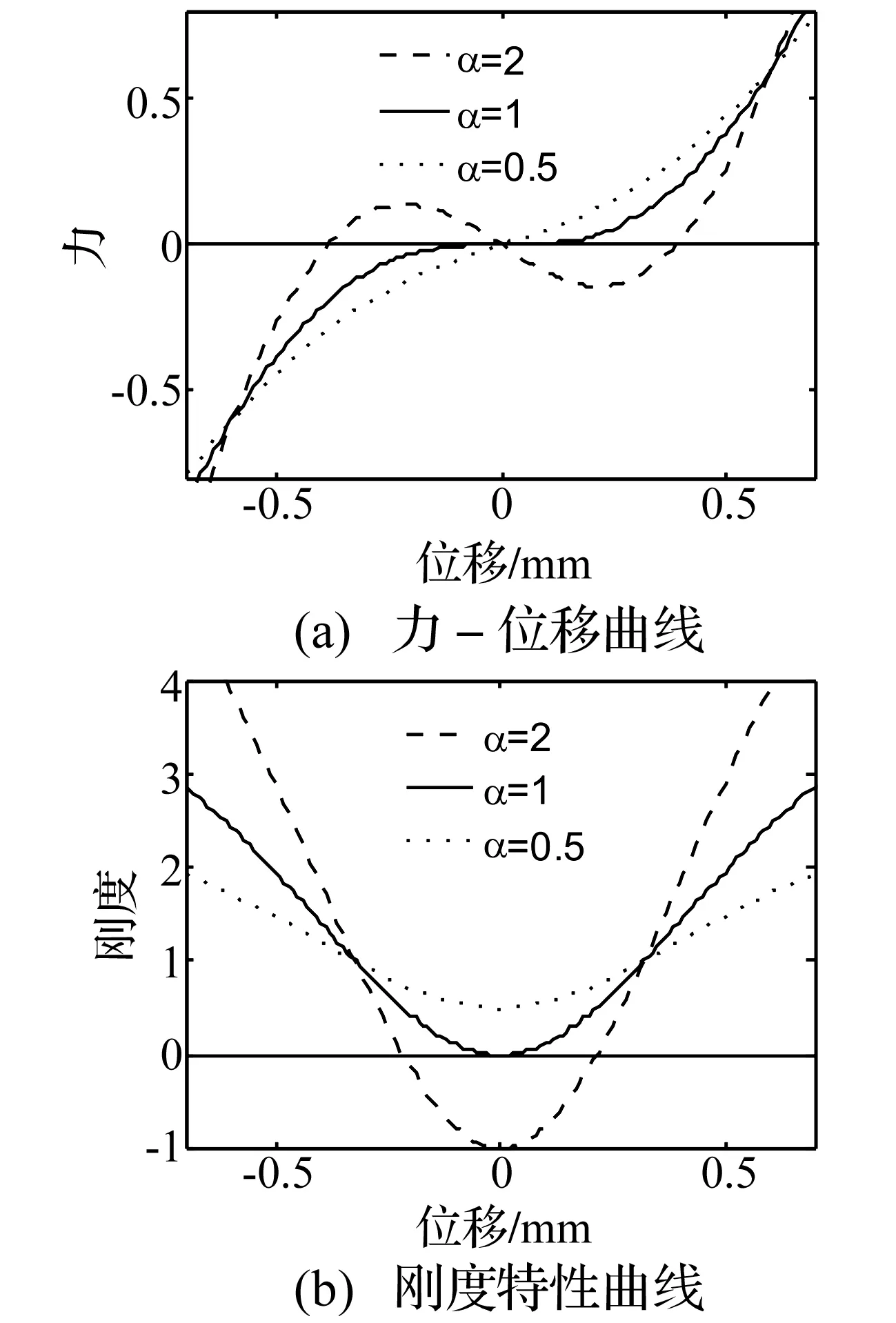
图2 当=0.8时，对于不同的α，系统的无量纲曲线

(5)

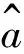
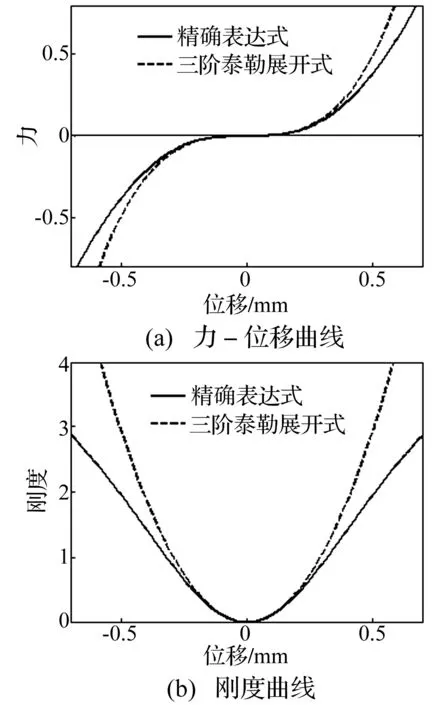
图3 当时，QZS系统曲线

(6)

则QZS系统刚度的近似表达式为：

(7)

1.2 QZS系统的运动方程

从前面的分析可知，QZS系统在其静平衡位置附近刚度很小。为了保证质量m的被隔振设备放于QZS系统上时，倾斜弹簧刚好被压缩到水平位置，静载完全由被压缩的竖直弹簧支撑，即系统处于静平衡位置，那么，设备质量m要满足条件：

f=kvh=mg⟹m=kvh/g

(8)

式中，kv满足式(5)，以保证系统具有QZS。

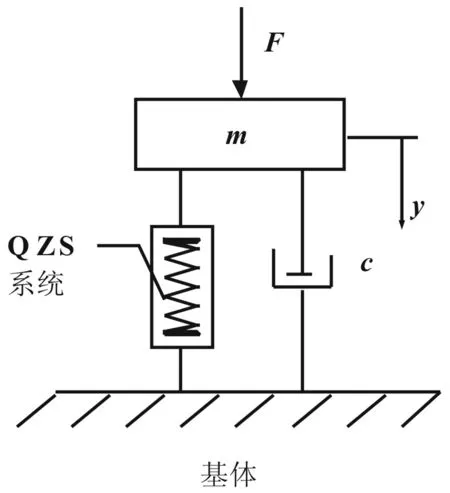
图4 承载质量m的QZS系统等效模型

在实验中，如图4所示，考虑阻尼c的影响，被隔振质量m使QZS系统刚好处于静平衡位置。在简谐激励f=Fcosωt作用下，系统在其平衡位置附近做小幅振动。若其弹性恢复力用三阶近似表达式代替，系统的无量纲运动方程可如下所示：

(9)

从运动方程(9)式可以看出，QZS系统是一个缺少线性项的达芬系统。

2 传递率

接下来主要分析系统的幅频特性、力传递率以及阻尼和激励幅值对传递率的影响。

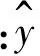
(10)

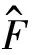
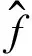
(11)

(12)

从(12)式可以看出，传递到基础上的力同样依赖于响应幅值A、阻尼比ζ、刚度γ以及激励频率Ω。传递率定义为传递到基础的力的幅值与激励力幅值之比，那么传递率T：

(13)

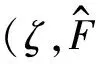
阻尼比对力传递率的影响如图5所示。从中可以看出，阻尼比对系统的振动衰减性能很敏感。当阻尼比ζ=0.01时，系统存在跳跃现象，传递率曲线在很大程度上向右弯曲，这表明阻尼比过小时衰减结果并不理想。当阻尼比ζ=0.15时，共振区附近的振动显著减小，衰减频域被拓宽，但是高频区的衰减效果变差。当阻尼比ζ=0.4时，跳跃现象消失，振动衰减情况与上述类似，低频区隔振效果显著，而代价是高频区的隔振效果更差。从上述可见，随着阻尼比的增大，跳跃区间[8]逐渐减小，当跳下频率等于跳上频率即跳跃区间等于零时，跳跃现象消失，此时的阻尼比即为临界阻尼比。只要系统阻尼比大于其临界阻尼比，系统中就不会再出现跳跃现象。

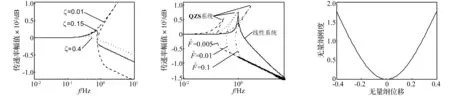
图5 当γ=5，=0.1时，阻尼比ζ对系统力传递率的影响

3 实验研究

为了评估所设计的QZS系统的隔振性能，开展了一系列的实验工作。首先介绍实验设备及其安装过程，然后展示实验结果及结果分析。

3.1 实验装置

QZS系统的试验装置如图8所示，其相应的参数如表1所示。表1中的参数可以用来验证实验系统是否存在QZS特性。图7给出了实验模型在其平衡位置附近的刚度曲线。从中可以看出，在静平衡位置系统具有零刚度特性。

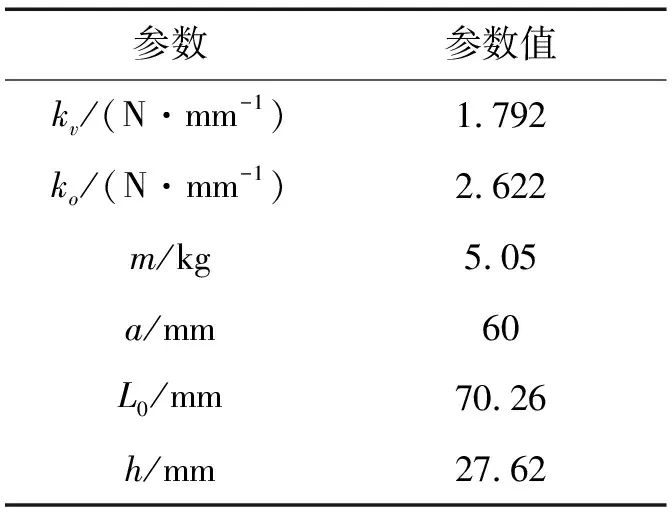
表1 实验装置的物理参数

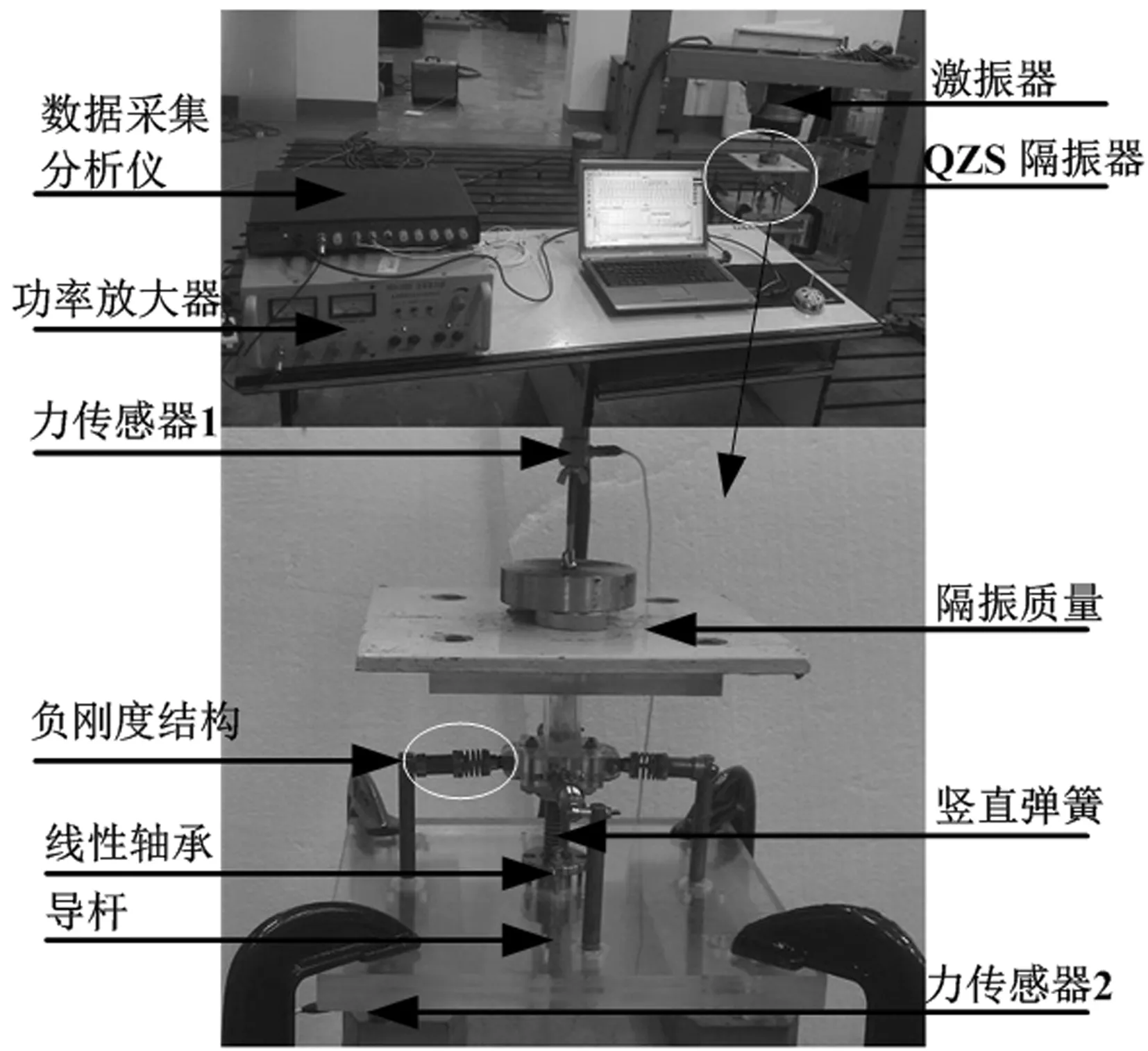
图8 实验装置照片

QZS系统的实验装置照片如图8所示。被隔振质量块由竖直弹簧支撑。在质量块的正上方装有一个由功率放大器(型号HEA-200C)驱动的激振器(型号HEV-200)，此激振器用于提供竖向的激振力。在质量块与激振器之间，装有一个用于测量激振力的力传感器(型号208C02)。另一个力传感器(型号208C02)安装在QZS装置支撑板的下面，用于测量振动过程中被传递到基础上的力。由于阻尼对系统的动力学行为比较敏感，所以QZS系统的试验装置进行了多次修改以减小各运动部件间的摩擦。导杆可以通过线性轴承顺利地滑动。由ECON公司制造的数据采集与分析仪(型号AVANT-MI-6008)，用于采集传感器的输入输出信号。一台电脑用于处理整个测量系统的I/O数据操作。

3.2 隔振性能评估

本节用试验评估QZS系统的隔振性能。隔振性能用力传递率来评估，即传递至基础的力与激励力的有效值之比。将撤去倾斜弹簧后的线性系统作为对比隔振系统。外部激励力由激振器提供，直接作用在质量块上，激励频率带宽从0.5 Hz到20 Hz。

在介绍实验结果之前，有关实验操作中的几个问题需要加以说明。首先，与线性系统不同，QZS系统的传递率受激励力幅值的影响，为了使线性系统与QZS系统之间传递率的比较有意义，实验中两者的激励条件应保持一致。

第二，选择既适合线性系统又适合QZS系统的激励力是不容易的。为了防止实验装置被损坏，对于线性系统而言在其共振区附近采用较小的激励力是非常必要的。然而对于QZS系统而言却不能采用同样的激励力，具体原因会在下面详述。由振动理论可知，在线性系统中传递到基础的力与激励力是成正比的。所以，为了使两系统之间被传递到基础的力的比较有意义，将线性系统传递至基础的力乘以一个放大因子，即QZS系统与线性系统的激励力幅值之比。

第三，为了展示QZS系统良好的隔振效果，选择大小合适的激振力是非常必要的。虽然仿真结果没有揭示，但实验测试结果却一再表明，QZS系统的优良的隔振性能对小振幅振荡是不敏感的。这是因为在小振幅振动中，QZS系统的负刚度因素没有发挥重要作用。因此，在小幅振动状态下，QZS系统与线性系统的隔振性能差异很小，而在大振幅振动状态下，大位移范围内QZS系统的正负刚度互相抵消，呈现出良好的隔振效果。值得一提的是，一般而言，较大激励力对应较大振幅响应，但在接近共振区和低频区域，小激励力也可以引起相对大的振幅，所以这里提到的大振幅并不对应大激励力。可参见表2中，激励力幅值随着频率增加逐渐变大。

最后需要指出的是，在整个实验过程中保持恒定的激励力是非常困难的。在激励力的作用下，系统在不同频率带的响应是不同的。在低频带，为了防止实验装置被损坏，选择较小的激励力。所以在实验过程中，系统在低频带的激励力是渐变的，一旦系统的振动处于安全范围之内，后续频域内的激励力幅值就设定在一个恒定值。

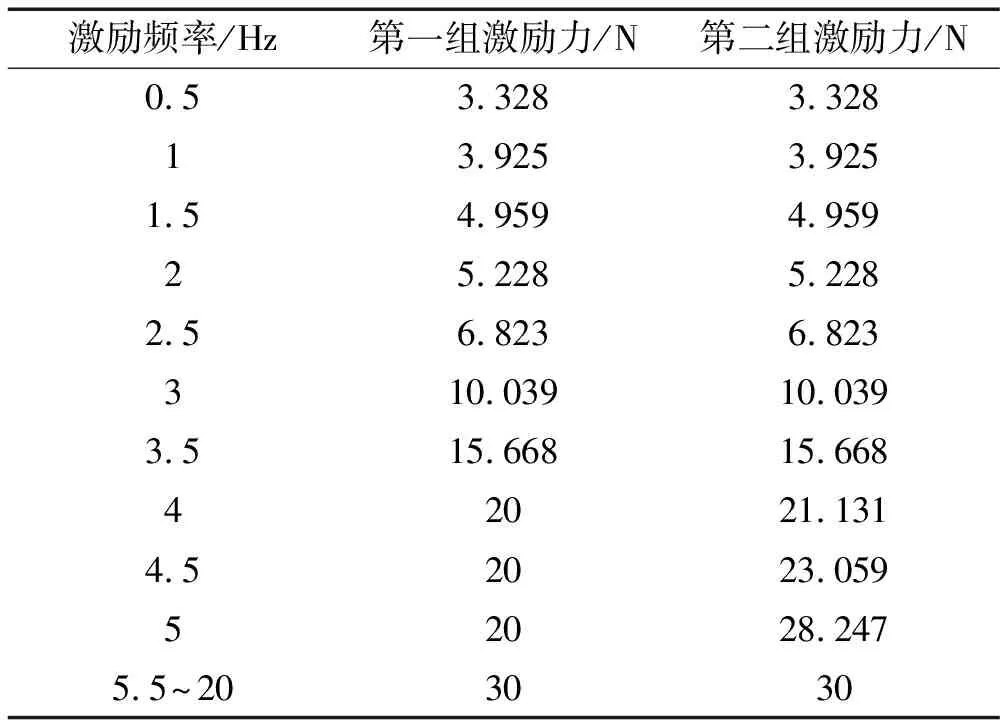
表2 实验所用正弦激励信号的频率和有效值

在实验中，设计两组不同的激励力进行测试，其目的是为了测试QZS系统在不同激励力下的隔振性能，测试所用的激励频率及其相应的激励力如表2所示。从中可以看出，在低频带激励力从小到大逐渐增加，第一组激励力在频率达到4 Hz以后一直保持在20 N，第二组在频率达到5.5 Hz以后一直保持在30 N。激励信号是正弦的，表2中给出的激励力都是力的有效值(力的均方根值)。

图9展示了系统在不同激励力作用下的传递率。在每组实验结果中，带点的实线表示的是QZS系统，带圆圈的虚线表示的是线性系统。从图中可以看出：第一，线性系统在大约3 Hz时达到共振峰值，而QZS系统没有出现共振；第二，QZS系统的有效衰减(传递率小于1)是从0.5 Hz开始的，而线性系统是从大约4.2 Hz开始的，这就意味着QZS系统非常有效地延长了隔振区间；第三，在0.5 Hz到10 Hz的低频带，QZS系统的传递率比线性系统低很多，特别是在线性系统的共振峰附近，而在高频带，QZS系统的隔振性能与线性系统几乎相当。综上所述，QZS系统非常适用于低频隔振。

前面的理论分析已经指出QZS系统对阻尼是敏感的。也就是说从理论上来讲，QZS系统有一个弯曲共振峰，但是只要系统阻尼大于其临界阻尼就能使共振峰消失，如前面图5所示。所以在实验时，弯曲共振峰的消失使系统不再共振，这是所提出系统的一个优点。

4 结 论

本文提出了一种由5个线性弹簧并联组成的QZS隔振装置，推导了静平衡位置处的零刚度条件。利用谐波平衡法得到了力传递率表达式。理论分析表明：随着阻尼的增加和激励幅值的减小，传递率共振峰值逐渐减小。

通过试验研究评估了QZS系统的隔振特性。结果表明，在低频范围内，QZS系统的隔振性能明显优于相应的线性系统，但在高频范围内，其隔振性能与线性系统相当。这表明QZS系统更适用于低频隔振。此外，在实验中观察到，QZS系统的隔振性能依赖于振动幅值，只有在一定的大振幅振动状态下，QZS系统才能表现出优良的隔振性能。

[1]Carrella A, Brennan M J, Waters T P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic[J]. Journal of Sound and Vibration, 2007,301 (3-5):678-689.

[2]Carrella A, Brennan M J, Waters T P. Optimization of a quasi-zero-stiffness isolator[J].Journal of Mechanical Science and Technology, 2007, 21 (6): 946-949.

[3]Carrella A, Brennan M J, Waters T P, et al. On the design of a high-static-low-dynamic stiffness isolator using linear mechanical springs and magnets[J]. Journal of Sound and Vibration, 2008,315 (3):712-720.

[4]Carrella A, Brennan M J, Waters T P. Optimization of a passive vibration isolator with Quasi-Zero-Stiffness characteristic, university of southampton[M]. Institute of Sound and Vibration Research, Dynamics Group, 2006.

[5]Carrella A, Brennan M J, Kovacic I, et al. On the force transmissibility of a vibration isolator with Quasi-Zero-Stiffness[J]. Journal of Sound and Vibration, 2009,322 (4-5):707-717.

[6]Kovacic I, Brennan M J, Waters T P. A study of a nonlinear vibration isolator with a quasi-zero stiffness characteristic[J]. Journal of Sound and Vibration, 2008,315 (3):700-711.

[7]Kovacic I, Brennan M J, Lineton B. Effect of a static force on the dynamic behavior of a harmonically excited quasi-zero stiffness system[J].Journal of Sound and Vibration, 2009,325 (4-5): 870-883.

[8]Brennan M J, Kovacic I, Carrella A, et al. On the jump-up and jump-down frequencies of the Duffing oscillator[J].Journal of Sound and Vibration, 2008,318 (4-5) 1250-1261.

[9]Gatti G, Kovacic I, Brennan M J. On the response of a harmonically excited two degree-of-freedom system consisting of a linear and a nonlinear quasi-zero stiffness oscillator[J]. Journal of Sound and Vibration, 2010,329 (10) 1823-1835.

[10]Platus D L. Negative-stiffness-mechanism vibration isolation systems[J]. Proceedings of SPIE-the International Society for Optical Engineering, 1999,3786: 98-105.

[11]Robertson W S, Kidner M R F, Cazzolato B S, et al., Theoretical design parameters for a quasi-zero stiffness magnetic spring for vibration isolation[J]. Journal of Sound and Vibration, 2009,326 (1-2):88-103.

[12]Zhou N, Liu K. A tunable high-static-low-dynamic stiffness vibration isolator[J].Journal of Sound and Vibration 2010,329 (9):1254-1273.

[13]刘兴天，张志谊，华宏星.新型低频隔振器的特性研究[J].振动与冲击，2012,31(5):161-164.

LIU Xing-tian, ZHANG Zhi-yi, HUA Hong-xing. Characteristics of a novel low-frequency isolator [J], Journal of Vibration and Shock, 2012, 31(5):161-164.