基于自适应响应面法的输电塔线体系腐蚀疲劳可靠度研究
张春涛, 范文亮, 鲁 黎, 李正良, 刘 潇
(1. 西南科技大学 土木工程与建筑学院,四川 绵阳 621010;2. 重庆大学 土木工程学院,重庆 400045;3.中机中联工程有限公司,重庆 400039)
输电塔线体系作为大型复杂结构体系,同时具有高耸结构和大跨度结构的共同特点,对风荷载作用十分敏感[1-2]。而且整个服役期内由于长期处于环境腐蚀和风致振动作用下,结构会产生腐蚀疲劳损伤累积,导致体系的抗力和性能逐步退化,从而降低结构抵抗极端环境作用的能力,致使结构实现预定功能的概率减小[3]。因此,随电力行业的发展环境腐蚀作用下输电塔线体系的风振疲劳可靠度问题不可忽略,为减少或避免由此带来的灾害,必须建立正确评估腐蚀疲劳耦合作用下输电塔线体系的可靠度分析方法。
输电塔线体系的可靠度是在空间桁架和大跨度结构体系的研究基础上发展起来的,受到了广泛关注。Natarajan[4]以风荷载为随机变量对输电塔的可靠度展开了研究,但是仅对风荷载进行研究还并不能真实反映结构的随机可靠性能;为此,Natarajan等[5]同时选取风荷载和结构构件抗力为随机变量对输电塔的体系可靠度进行了研究;石少卿等[6]在Natarajan的研究基础上,分析了塔架结构体系在极值型风荷载作用下的可靠性;高险峰等[7]在风洞试验的基础上,对高度为345.5 m的江阴长江大跨越500 kV输电塔进行了可靠性研究;与此同时,李杰等[8]亦采用概率密度演化方法对输电塔线体系的动力可靠度进行了研究;李宏男等[9]对杆型输电塔体结构的疲劳可靠性展开了研究;李茂华等[10]通过一次二阶矩方法对1 000 kV输电塔体结构的可靠性能进行了分析。
显然,上述学者对输电塔线体系可靠度的研究已取得了许多显著的成果。然而,上述研究一方面仅是对输电塔的风致动力可靠度进行了研究,而风振疲劳可靠度却由于构件S-N曲线模型的匮乏研究尚少;另一方面,研究中采用的基本理论又多是以一次二阶矩方法为基础展开的,计算量大,效率低下。于是,本文将原理简单、实现容易的响应面法拓展至体系可靠度分析领域。但是目前常用的响应面形式有含交叉项的完全二次多项式和不含交叉项的二次多项式。含交叉项的二次多项式虽然计算精度高,但是待定系数多,需要的抽样点亦多,计算效率低;不含交叉项的响应面法虽然待定系数少,应用方便,只需较少的结构分析即可,但是计算结果精度低。同时,不含交叉项亦意味着各轴之间并未被充分覆盖[11],这对于随机变量存在相互影响的情形(比如强非线性情形、荷载和结构参数均为随机变量的情形等)显然是不合理的。于是,Faravelli[12]通过引入误差修正项,Rajashekher等[13]引入交叉项和迭代选点,Zheng 等[14],Yu等[15]通过逐步引入二次项和交叉项对响应面法表达式进行了改进,虽然提高了计算精度,更具有合理性,但亦增加了计算难度,降低了计算效率,实现起来更为复杂。
为此,本文首先综合考虑精度和效率给出了响应面中交叉项是否存在的判断准则,并构造了相应的实现算法,从而建立了可以确定较为合理的含交叉项的二次响应面形式的自适应响应面法。同时,通过Q345等边角钢构件的腐蚀疲劳试验结果和概率论建立了构件腐蚀疲劳随机S-N曲线模型。最后,根据建议自适应响应面法和构件腐蚀疲劳试验结果对输电塔线体系进行腐蚀疲劳可靠性研究。
1 考虑交叉项的自适应响应面法
1.1 交叉项的判断准则
响应面法的完全二次多项式为
(1)
式中,a0,ai,aij为待定参数,共0.5n2+1.5n+1个。若以xi为基本变量,式(1)亦可表示为
(2)
式(2)可简化为
(3)
式中,f0为包含n-1个变量的二次多项式,f1为包含n-1个变量的一次多项式。显然,若f0和f1又以xj(j≠i)为基本变量进行改写,并分别记为φ0(xj)和φ1(xj),式(3)可进一步改写为
(4)
显然,式中φ0(xj)和φ1(xj)均为多项式且系数仅包含n-2个变量,若这n-2个变量均取为常数,则两者即为xj的一元多项式。
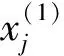
(5)
显然
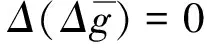
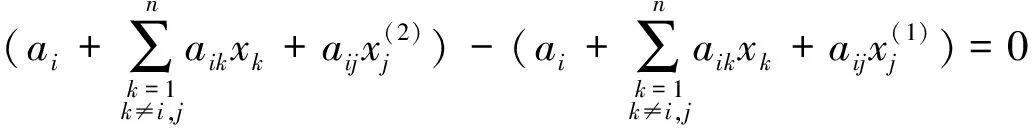
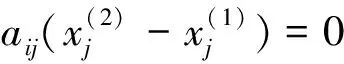
(6)
1.2 自适应响应面法
根据1.1的交叉项判断准则,基于式(1)可以获得自适应响应面的表达式
(7)
式中,I[xixj]为xixj的示性函数,即
根据交叉项的判断准则,可给出自适应响应面法的实现步骤如下:
(1) 若Xi~N(μi,σi),分别取xi=μi和xi=μi+kσi(k为给定常数),其余变量均取均值;若Xi为非正态变量,则xi可取与上述取值具有相同超越概率的值。对i=1,…,n重复上述步骤可给出n+1个样本点;
(2) 取xi=μi+kσi(i=1,…,n)和xj=μj+kσj(j>i),其余n-2个变量取均值,共确定(n2-n)/2个样本点;
(3) 根据上述样本点计算每组随机变量的对应函数值,对任意两随机变量可得到Δg=g(x1,…,xi+kσi,…,xn)-g(x1,…,xi,…,xn)和Δg=g(x1, …,xi+kσi,…,xj+kσj,…,xn)-g(x1,…,xi,…,xj+kσj,…,xn)。根据交叉项的判断准则,若两差值不等,则变量xi和xj之间存在相互影响,多项式中含有交叉项xixj,即式(7)中I[xixj]=1;若两差值相等,则多项式中不存在交叉项xixj,式(7)中I[xixj]=0。
(4) 再增加n个样本点,即xi=μi-kσi,其余变量取均值。只要k选择合理,可保证极限状态曲面穿过样本点区域,从而具有较高的精度,参考文献[5]的研究,可取k=3;
(5) 利用上述样本点可方便的拟合出自适应响应面。为改善以均值点为中心选点的不足,文中亦借鉴Bucher & Bourgund的迭代改进思想,即先由上述响应面确定验算点X*,再由下式确定新的选点中心XM
(8)
式中,μ代表均值点。然后,以XM为中心,类似于步骤(1)和(4)可确定新的2n个样本点。
(6) 根据上述样本点可给出最终的响应面,最后可对此响应面利用Monte Carlo法等计算可靠度。
2 腐蚀疲劳随机S-N曲线方程的建立
2.1 试验概况
本次试验通过MTS电液伺服加载系统(如图1所示)对70 mm×5 mm的Q345等边角钢进行了腐蚀疲劳试验,加载频率为4 Hz。根据角钢构件在输电塔体中的连接构造要求对试件进行开孔加工,孔洞直径为20 mm,试件最终加工状态如图2所示。

图1 MTS电液伺服加载系统
试验中首先利用浓硫酸、硝酸、盐酸和蒸馏水按照一定比例配置成PH值为2的酸性溶液[3]。然后,采用"浸泡-晾置"间浸式腐蚀方式腐蚀试件,即首先将试件在酸性溶液中浸泡2 h,然后取出试件再在空气中晾置2 h,如此"浸泡-晾置"往复循环3次,共计12 h为一次完整腐蚀。腐蚀疲劳试验中采用"腐蚀-疲劳"交替循环加载方式,即先采用上述腐蚀方式将试件腐蚀12 h后,再进行疲劳振动。按此思路,为了研究Q345等边角钢疲劳性能随腐蚀时间的变化规律,分别对四组试件进行试验,其中一组为纯疲劳试验;其余三组为腐蚀疲劳试验,分别"腐蚀-疲劳"交替循环2次、3次和4次,腐蚀时间t1、t2和t3分别为24 h、36 h和48 h。同时,各组试件的等幅疲劳荷载水平均相同,共6级。每级荷载水平均采用一个角钢构件进行单点试验。
2.2 试验结果
各组试件经不同“腐蚀-疲劳”循环次数后的疲劳寿命如表1所示。

表1 不同腐蚀时间的疲劳寿命试验结果
根据文献[3]建议的单点-似然法实现算法,由表1的试验数据可以确定出任意可靠度P时试件随腐蚀时间变化的腐蚀疲劳t-P-S-N曲线方程,P=99%时,曲面方程为
(9)
由上式绘制出不同腐蚀时间的99%-S-N曲线和试验结果如图3所示
2.3 随机S-N曲线方程
首先,由上述试验结果可以建立具有不同可靠度的腐蚀疲劳t-P-S-N曲线方程。由此曲线方程,分别计算出腐蚀时间等于0 h、25 h、50 h、75 h、100 h、125 h和150 h七个等级时,不同可靠度P对应的疲劳寿命Np。然后,将不同腐蚀时间内的各疲劳寿命Np与P=50%的疲劳寿命N0.5相除,得到不同可靠度P对应的疲劳寿命与平均疲劳寿命的比值γ。最后,根据P与比值γ分布情况,由常用的疲劳寿命分布函数正态分布和三参数Weibull分布函数计算出的超值累积频率曲线如图4所示。
不难发现,相同腐蚀时间内正态分布和Weibull分布曲线与计算值吻合良好,差异较小;但是与正态分布曲线相比,Weibull分布的吻合性更好,更能真实反映出γ的超值累积频率的变化情况。同时,腐蚀时间对γ的P值亦存在显著影响。例如,γ为0.9时,与腐蚀时间为0 h的可靠度P值相比,腐蚀时间分别为50 h、100 h和150 h时,采用正态分布计算的P值分别增加了6.37%、12.12%和16.28%,而采用Weibull分布计算出的P值增加幅度相对较小,增加的百分比分别为3.44%、6.69%和14.75%。因此,Weibull分布能够更加准确合理地反映γ的分布情况。

图3 腐蚀时间对构件腐蚀疲劳P-S-N曲线的影响
根据不同腐蚀时间作用下比值γ及其对应P值可以拟合出对应Weibull分布的参数值见于表2。显然,随腐蚀时间增加试件抗疲劳性能降低,疲劳寿命与均值之间的偏差较小。计算值亦表明了Weibull分布各参数随腐蚀时间的变化规律:特征参数α随腐蚀时间增加而降低,腐蚀时间由0 h增加到50 h、100 h和150 h时,α分别降低了18.20%、33.63%和46.44%;形状参数β和最小比值υ随腐蚀时间增加而增大,腐蚀时间增加到50 h、100 h和150 h时,β分别增加了5.02%、9.18%和12.75%,而υ的增加幅度与β大致相同,分别增加了5.13%、9.55%和13.26%。
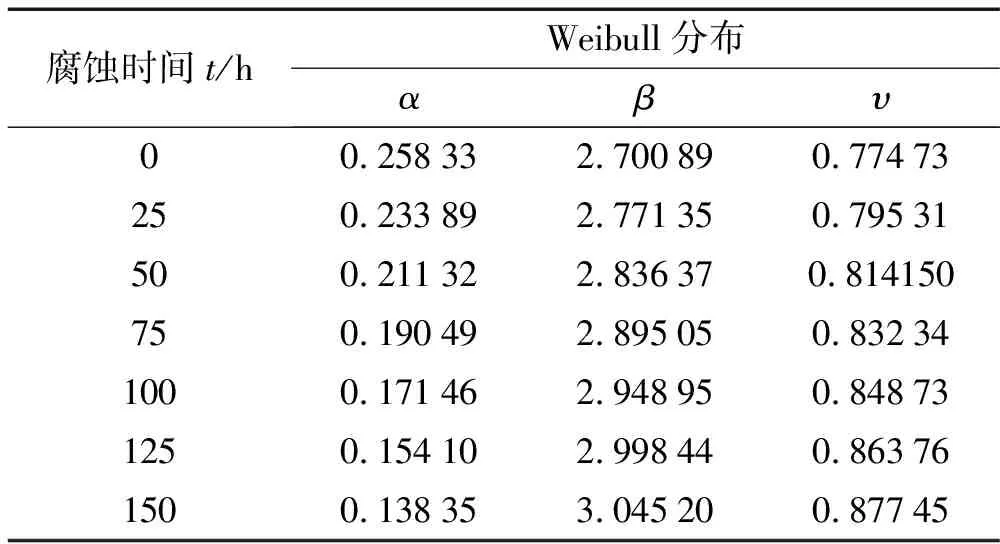
表2 分布函数参数
首先,由表2中各参数值随腐蚀时间的变化规律建立与之对应的变化式α(t)、β(t)和υ(t);然后,再将各参数变化式代入分布函数即可得到随腐蚀时间变化的Weibull分布函数表达式为
(10)
式中,各参数随腐蚀时间t的变化式为
(11)
β(t)=3.551 46-
(12)
υ(t)=1.042 49-
(13)
显然,将式(11)和式(13)代入式(10)即能给出随腐蚀时间变化的Weibull分布表达式,并绘制出相应的概率密度变化曲面,如图5所示。曲面形象地反映出了随腐蚀时间t增加,随机变量γ取值的离散程度逐渐减小的变化规律。若将随机变量γ代入可靠度P为50%的S-N曲线方程,便可得到随机腐蚀疲劳S-N曲线表达式
N=γ·N0.5=
γ·f(Smax,t)=
(14)
3 输电塔线体系疲劳可靠性分析
本节以风速V、腐蚀时间T、以及S-N曲线随机因子γ作为随机变量,采用文中建议自适应响应面法拟合出输电塔线体系的极限状态曲面并进行可靠度分析。其中,随机变量风速V~N(11,1.35)和腐蚀时间T~N(1 018,98);前已述及Weibull更能真实地反映γ的超值累积频率的变化情况,因此,确定样本点时概率密度函数采用式(10)。塔体服役期为100年[2],损伤[D]为1。

图7 输电塔分段示意图
3.1 腐蚀疲劳损伤计算
首先,根据自适应响应面法的实现算法构造出样本点,再由样本点中各风速值按文献[2,16-17]的方法拟合出不同的风速功率谱并转化为气动力。然后,对输电塔线体系进行时程分析,找出结构中最不利受力杆件(关键杆件)的应力时程,并采用雨流计数法对应力时程进行整理统计,得到各应力幅及其在整个时程分析中出现的次数,再由文中建立的随机腐蚀疲劳S-N曲线模型(即式(14))确定各应力幅的疲劳寿命;最后,结合各应力幅出现的次数和对应的疲劳寿命采用Miner准则计算出该平均风速对应功率谱对结构构件造成的实际损伤,由此损伤亦可确定构件或结构的疲劳寿命。
具体计算过程为:由上述步骤可计算出某平均风速对应风速功率谱作用下输电塔线结构体系中待研究杆件的应力时程[σi](应力幅个数i=1,2…,k),并通过雨流法得到应力幅矩阵
S=[S1,S2,S3,…,Sk]
(15)
显然,将式(15)确定的应力幅和各样本点中的t和γ代入式(14)可计算出各应力幅对应的疲劳寿命矩阵,即
N=[N1,N2,N3,…,Nk]
(16)
同时,由雨流计数法经统计分析可得到整个计算期内式(15)中各等效应力幅出现的循环次数
n=[n1,n2,n3,…,nk]
(17)
根据Miner累积损伤理论,即可得到杆件的损伤矩阵
(18)
由式(18)即可计算出各平均风速的模拟风场在计算期对构件造成的损伤。
3.2 疲劳损伤可靠性分析
腐蚀疲劳作用下结构可靠度功能函数可表示为
g(x)=D-d(x)
(19)
式中,d(x)表示由式(18)确定的腐蚀疲劳损伤值,x=(v,t,γ)表示基本随机变量。显然,d(x)为隐式函数,因此g(x)亦为隐式函数,可用建议自适应响应面法拟合出g(x)的显示表达式并求解其可靠度,具体计算过程如下:
① 由交叉项判断准则确定交叉项vt、vγ和γt的存在性。根据建议算法,首先由1.2节步骤(1)~(2)选取4个样本点,再按步骤(3)判断交叉项是否存在,并确定自适应响应面的形式,详细过程示于表3。

表3 自适应响应面形式的确定过程
② 按照步骤(4)确定初始响应面为
g(x)=2.421 6+1.114 7v-0.001 4t-10.027 5γ
-0.074 2v2-4.086 9×10-7t2+
5.339 6γ2+0.000 14vt
(20)
利用Monte Carlo法可计算出失效概率为22.88%(抽样数为1×105,下同)。
③ 同时由JC法给出其验算点X*的坐标为(13.1, 1 018.4,1)。然后,根据步骤(5)可确定新的选点中心和其他6个新的样本点。综合利用上述样本点进行回归分析,可确定最终的自适应响应面为
g(x)=-6.311 2+0.834 1v+0.004 0t+4.590 1γ
-0.060 3v2-3.697 6×10-6t2-
2.044 6γ2+0.000 2vt
(21)
与之对应的失效概率为36.92%。
同时,采用传统的不含交叉项的响应面法,根据Bucher选点方案,通过两次迭代得到的响应面为
g(x)=-7.589 6+0.958 1v+0.005 1t+4.430 7γ
-0.056 68v2-3.011 88×10-6t2-2.038 18γ2
(22)
对应的失效概率为19.52%。显然,式(21)因为考虑了存在相互影响的随机变量之间的交叉项,其失效概率与不考虑交叉项的式(22)存在较大差异。最后,由文献[3]的方法,采用ANSYS中的Monte Carlo法即可验证结构可靠度分析中建议自适应响应面法的有效性。
4 结 论
本文首先通过严格的数学推导给出了交叉项是否存在的判断准则,考虑了相互影响随机变量之间的交叉项,舍弃了不存在的交叉项,建立了更为合理和精确的自适应响应面法。同时,为了克服传统材性试件S-N曲线模型的不足,文中通过Q345等边角钢的腐蚀疲劳试验建立了构件随机腐蚀疲劳S-N曲线模型。最后,结合自适应响应面法和构件随机S-N曲线模型对输电塔线体系进行了疲劳可靠性分析,验证了随机变量交叉项判断准则能有效地保留相互影响随机变量之间的交叉项;建议自适应响应面法在保证精度的同时能显著减少计算量;构件随机腐蚀疲劳S-N曲线模型在结构可靠度分析中既简单易行又能考虑构件截面形式的影响。
[1]肖正直. 特高压输电塔风振响应及等效风荷载研究[D].重庆:重庆大学2009,5.
[2]汪之松. 特高压输电塔线体系风振响应及风振疲劳性能研究[D].重庆:重庆大学,2009,9.
[3]张春涛. 腐蚀环境和风振疲劳耦合作用下输电塔线体系疲劳性能研究[D]. 重庆: 重庆大学, 2012, 12.
[4]Natarajan K. Wind load analysis-probabilistic approach national seminar on analysis and design for wind loads[J]. Indian Concrete Institute (ICI), Madras, 1991:35-46.
[5]Natarajan K,Santhakumar A R. Reliability-based optimization of transmission line towers [J]. Computers & Structures, 1995, 55(3):387-403.
[6]石少卿, 童卫华, 姜节胜,等. 极值型风荷载作用下大型结构可靠性分析[J]. 应用力学学报, 1997, 14(4): 142-147.
SHI Shao-qing, Tong Wei-hua, Jiang Jie-sheng, et al.. System reliability analysis of large structure under Gumbel distribution wind loads [J]. Chinese Journal of Applied Mechanics, 1997, 14(4): 142-147.
[7]高险峰, 屠海明.江阴长江大跨越输电塔节段静力试验模型可靠度分析[J]. 特种结构, 2004, 21(3):15-17.
GAO Xian-feng, TU Hai-ming. Reliability analysis of mockup experiment of Jiang Yin long-span transmission tower [J]. Special Structures, 2004, 21(3):15-17.
[8]李杰, 何军, 李天.大型电力网络系统抗震可靠度分析[J].哈尔滨建筑大学学报, 2002, 35(1): 7-11.
LI Jie, HE Jun, LI Tian. Seismic reliability analysis of large electric power systems [J]. Journal of Harbin University of Cvil Engineering & Architecture, 2002, 35(1): 7-11.
[9]李宏男,白海峰. 输电塔线体系的风(雨)致振动响应与稳定性研究[J]. 土木工程学报, 2008, 41(11):31-38.
LI Hong-nan, BAI Hai-feng. Dynamic behavior and stability of transmission tower-line system under wind (rain) forces[J]. China Civil Engineering Journal, 2008, 41(11):31-38.
[10]李茂华. 1 000kV级特高压输电杆塔结构可靠度研究[D].重庆:重庆大学,2012,4.
[11]Bucher C G, Bourgund U. A fast and efficient response surface approach for structural reliability problems[J]. Structural Safety, 1990, 7(1): 57-66.
[12]Faravelli L. Response surface approach for reliability analysis[J]. Journal of Engineering Mechanics, 1989, 115(12): 2763-2781.
[13]Rajashekher M R, Ellingwood B R. A new look at the response surface approach for reliability analysis[J]. Structural Safety, 1993, 12(3): 205-220.
[14]Zheng Y, Das P K. Improved response surface method and its application to stiffened plate reliability analysis[J]. Engineering Structures, 2000, 22(5): 544-551.
[15]Yu L, Das P K, Zheng Y L. Stepwise response surface method and its application in reliability analysis of ship hull structure[J]. Journal of Offshore Mechanics and Arctic Engineering, 2002, 124(4): 266-270.
[16]张春涛,李正良,范文亮,等.考虑风向风速联合分布的输电塔线体系风振疲劳研究[J]. 工程力学, 2013, 30(3): 315-322.
ZHANG Chun-tao, LI Zheng-liang, FAN Wen-liang, et al.. Study on wind-induced fatigue of transmission tower-line coupled system considering the joint distribution of wind speed and wind direction [J]. Engineering Mechanics, 2013, 30(3): 315-322
[17]张春涛,李正良,范文亮,等.遮挡山体对输电塔线体系风振疲劳的影响[J]. 振动与冲击, 2013, 32(10): 184-191.
ZHANG Chun-tao, LI Zheng-liang, FAN Wen-liang, et al.. Effect of occluding hills on wind-induced fatigue of transmission tower-line coupled system [J]. Journal of Vibration and Shock, 2013, 32(10): 184-191.

