三维耦合Timoshenko梁功率流主动控制研究

王有懿，赵 阳，马文来

(哈尔滨工业大学 航天学院，哈尔滨 150001)

三维耦合梁结构广泛应用于航天与土木建筑工程中，例如由三维耦合梁结构组成的航天器空间桁架结构因其质量轻、灵活及易拆装等特点，将会成为未来航天器的主体承力结构。飞轮和陀螺等高速旋转部件工作时产生的中、高频扰动在航天器梁式结构中传播，将会引起结构不必要的振动。由于太空中阻尼较小，这种振动一旦发生很难衰减，将会影响其支撑的高精度有效载荷的正常工作[1]。因此，对三维耦合梁结构进行振动分析与控制研究是十分迫切和必要的。

结构振动的功率流综合了力和速度响应大小及相位关系，能够给出结构内的局部能量分布和功率流的传播路径，揭示整个系统的能量分布，是研究复杂系统振动的有效工具。在低频段，基于模态叠加的有限元法适用于振动功率流的求解，但在求解中高频问题时，需要划分更多的单元，考虑更多的高阶模态，计算量变得十分庞大，而高阶模态计算本身不准确，从而导致相应的中高频功率流计算结果不准确。统计能量法仅仅适用于高模态密度的高频域振动功率流的计算，且只能得到全域的平均信息，无法获得具体位置的功率流。行波方法[2]则从振动的本质出发，完整地回答了振动传播的根本问题，其可以精确计算结构振动的功率流。行波方法一般不受分析频率的限制，更具有鲁棒性。

自Goyder等[3]提出功率流的基本概念以来，功率流方法就被作为振动控制研究的分析工具。功率流主动控制方法克服了传统模态控制方法和数学模型紧密相关及控制频率受限的缺点和不足，其基本观点是隔离结构中能量的传递，仅仅通过最小化功率流就可以达到减小结构整体抖动的目的。功率流模型可以用来描述结构中的振动传播，是振动控制设计中一个很重要的控制优化特征量。Pan等[4]推导了弯曲、扭转和纵波的功率流表达式，并研究了无限长梁结构的功率流主动控制。Schwenk等[5]提出了一种用于控制梁结构振动功率流的算法。Audrain等[6]研究了梁结构的功率流控制理论，并进行了实验验证。Pereira等[7]采用基于最小化结构功率流实部的控制方法，实现了梁结构整体抖动的降低。Liu等[8]采用行波方法研究了有限二维L型梁结构的功率流主动控制。朱宏平等[9]采用导纳波动方法研究了建筑结构的功率流主动控制策略。宋孔杰等[10]对柔性隔振系统的功率流理论进行了深入研究。伍先俊等[11]研究了主动隔振系统中反馈控制的功率流计算方法。金全洲等[12]研究了圆柱壳结构的功率流主动控制方法。上述研究对梁结构的功率流分析与主动控制主要采用的是Euler-Bernoulli经典梁理论,这种理论在进行结构动力学分析时具有局限性，Timoshenko梁理论考虑了横向剪切变形和转动惯量的影响,能够更为全面的反映梁结构的动力学特性，特别适合中高频问题的分析，且其分析结果更接近工程实际。陈荣等[13]基于Timoshenko梁理论进行了斜置隔振系统的功率流分析，Beale等[14]考虑结构中弯曲波、纵波与扭转波的影响，使用波散射法分析了二维与三维结构的功率流，为了精确获得结构的中高频特性，弯曲波的分析采用Timoshenko梁模型。上述对Timoshenko梁的研究仅限于功率流的计算，而没有进一步研究功率流的控制问题。王有懿等[15]基于 Timoshenko梁理论研究了一维悬臂梁结构的功率流主动控制，但在此研究中仅考虑梁中弯曲波的影响。

因此，本文在文献[14-15]研究的基础上，基于Timoshenko梁理论，考虑三维耦合梁中弯曲波、纵波与扭转波的共同作用，建立了三维耦合梁结构的行波动力学模型，并获得了其结构中传播的功率流；并以此为目标函数，进行了基于主动功率流的控制研究；进行数值仿真分析，对比Euler-Bernoulli理论与Timoshenko梁的功率流结果；并分析了三维耦合梁结构中纵波与扭转波对结构总功率流的影响；进一步从频域与空间域研究了功率流主动控制方法的控制效果，并分析了最优控制力偏差和误差传感器位置对功率流主动控制效果的影响。

1 三维耦合梁结构行波动力学模型

如图1所示的三维耦合梁结构可以看成一维波导(结构单元)通过结点(边界)连接而成，在每个结构单元中存在弯曲波、纵波与扭转波，单元的动力学模型由波动方程描述。在结点处，存在弯曲波、纵波与扭转波之间的相互转换,所有外力和位移边界条件作用于结点。为了获得更为精确的结构中高频动力学特性,考虑剪切变形和转动惯量的Timoshenko梁模型用来进行单元弯曲运动的分析。

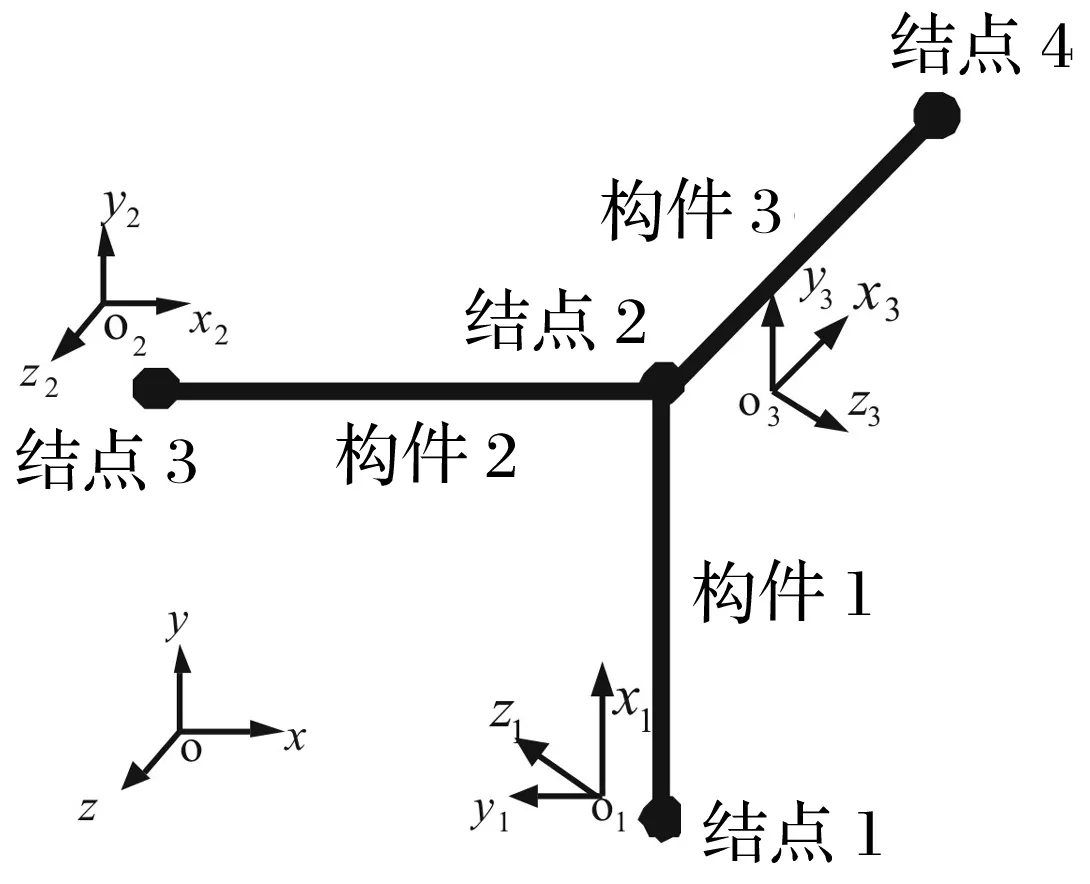
图1 三维耦合Timoshenko梁模型

1.1 单元模型

梁纵向运动的波动方程为：

式中：u和N分别为纵向位移和纵向力，ρ为材料密度，A为截面积，E=ER(1+iη)为复弹性模量，η为损耗因子，ω为圆频率。

根据行波理论，梁纵向位移的行波解[14]为：

u(x)=uleikxx+ure-ikxx

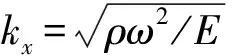
(1)

由于Timoshenko梁模型包含剪切变形和转动惯量的影响，其弯曲运动的波动方程为：

式中：w和φ分别为横向位移和转角，M和V为弯矩和剪力，G为剪切模量，I为梁的惯性矩，k为剪切折算系数，且k=π2/12。

根据行波理论，梁横向位移与转角的行波解[14]为：

k1=-k3=

s1=ρω2/E,s2=ρω2/kG,s3=A/I

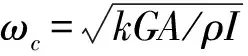
弯曲波在y方向的状态变换方程如下所示，对z方向的弯曲运动可同样导出类似方程。

(2)

梁扭转运动的波动方程为：

式中,φ为扭转角，T为扭矩，GJ为扭转刚度，IP为梁的截面极惯性矩。

根据行波理论，梁扭转角的行波解为[14]：

φ(x)=φleikTx+φre-ikTx

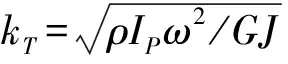
(3)

对同时存在纵向、弯曲、扭转运动的三维耦合梁结构，由式(1)-(3)得单元状态变换方程为：

(4)

式中：u=[uxwywzφxφyφz]T为截面位移向量，f=[NVyVzTMyMz]T为截面内力向量，wl=[ulwy1wz1φlwz2wy2]T为左行波向量，wr=[urwy3wz3φrwz4wy4]T为右行波向量，上标T为转置符号，Yul、Yur、Yfl、Yfr为单元状态矩阵。

单元传递方程表示为：

(5)

其中：t1(x2-x1)和t2(x2-x1)为单元传递矩阵。

1.2 结点散射模型

在结点上有外力及位移边界条件作用，因而需要满足位移连续及力平衡方程。

设一个结点有N个单元与之相连，在第n个单元上相对结点有入射波wni和出射波wno。由单元状态变换式得：

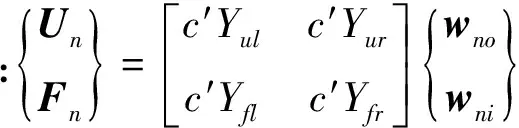
(6)

式中：c′为坐标变换矩阵。

由结点处的力平衡和位移协调条件得：

U1=U2=…=UN

(7)

式中，δ为作用在结点上的位移激励，Q为作用在结点上的外力，α,β为位移边界条件选择矩阵。

定义结点出射波向量为wo=[w1o,w2o,…wMo]T，结点入射波向量为wi=[w1i,w2i,…,wNi]T，将式(6)代入式(7)可得结点散射方程：

wo=Snwi+GnRn

(8)

式中Sn为结点散射矩阵，Gn为结点影响矩阵，Rn为作用在结点上的外激励向量。

1.3 系统总体方程

针对第m个单元，令单元出射波向量为wmo=[wo2wo1]T单元入射波向量为wmi=[wi2wi1]T定义系统出射波向量和入射波向量分别为：Wo=[W1o,W2o,…WMo]T,Wi=[W1i,W2i,…,WMi]T，其中M为单元数。

类似于有限元方法中刚度阵和质量阵的叠加方式，将所有结点散射方程(8)叠加得：

Wo=SWi+GR

(9)

式中S称为系统散射矩阵，G为系统影响矩阵，R=[R1,R2,…,RJN]T，JN为结点总数。

由单元传递方程(5)进行单元叠加得：

Wo=TWi

(10)

式中，T为系统传递矩阵。

联立方程(9)和(10)可得：

Wi=(T-S)-1GR

(11)

给定外激励R即可求得Wi和W0，并运用单元状态变换方程和传递方程式(4)-(5)可求得任意截面处的内力与位移：即获得了三维耦合梁结构的动力学响应。由于行波方法不受模态的限制，且在建模过程中采用Timoshenko梁理论，考虑了剪切变形与转动惯量的影响，因而其获得的中高频动力学特性将更为精确。

2 三维耦合梁结构中的功率流传播与主动控制

三维耦合梁功率流主动控制方法的基本思想是施加控制力耗散由扰动力产生的输入功率流，从而通过耗散输入能量来抑制结构整体的振动。其一般实现方式为：最小化误差传感器位置处扰动力和控制力产生的总功率流，从而获得最优控制力的大小和相位，并将最优控制力施加于结构以此耗散扰动力产生的输入功率流，最终通过减小结构中传递的功率流(综合了力和速度响应大小与相位关系)达到减小结构整体振动量级的目的。

结构的功率流表示为结构中某一截面能量传递的时间平均。在三维耦合梁结构中某一x位置截面处的主动功率流可表示为[15]：

(12)

式中：um=[Yu1Yur]wm为位移向量，fm=[Yf1Yfr]wm为内力向量，*为共轭转置符号，Re表示取实部。

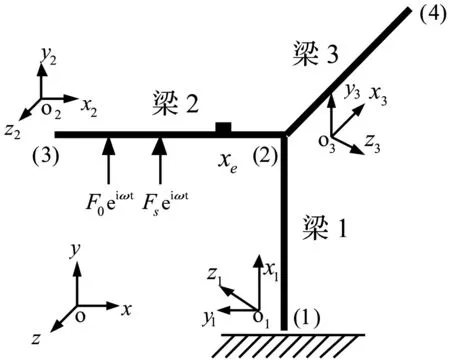
图2 三维耦合Timoshenko梁功率流主动控制图

如图2所示的三维耦合Timoshenko梁，作用于x0位置的扰动力F0eiωt在任意截面位置的位移向量和内力向量可以表示为：

u0(x)=ux0(x)F0,f0(x)=fx0(x)F0

(13)

式中：ux0(x)，fx0(x)为作用于x0位置的单位力产生的位移向量和内力向量。

同理：作用于xs的控制力Fseiωt在任意截面位置的位移向量和内力向量分别为：

us(x)=uxs(x)Fs,fs(x)=fxs(x)Fs

(14)

式中：uxs(x)，fxs(x)的形式和意义与ux0(x)，fx0(x)相同，仅仅是主动控制力Fseiωt作用位置处的连续条件不同。

由式(13)、(14)可得：当扰动力和控制力共同作用时，任意截面位置处的位移向量和内力向量为：

u(x)=ux0(x)F0+uxs(x)Fs

f(x)=fx0(x)F0+fxs(x)Fs

(15)

将式(15)代入式(12)得：

(fx0(x)F0+fxs(x)Fs)}

(16)

由在误差传感器位置x=xe，主动功率流Pxa对控制力Fs的实部和虚部偏导数为0，可得最优控制力为[15]：

(17)

式中：xe为误差传感器的位置，

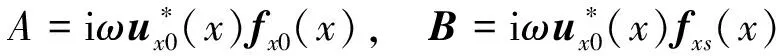
把式(17)代入式(16)可得通过三维耦合梁x截面的最小功率流。即通过优化功率流获得了控制力的大小与相位，通过自适应前馈控制方法施加控制力，以此实现了三维耦合梁功率流传播的主动控制。

3 仿真算例与分析

以悬臂三维耦合Timoshenko梁为例进行数值计算分析，首先采用行波方法计算其动力学响应并与有限元法计算结果进行比较，分析行波方法计算结构动态特性的精确性；在此基础上，基于Timoshenko梁理论获得了结构中传播的主动功率流，并与Euler-Bernoulli经典梁结果进行对比；进一步分析纵波与扭转波对结构总功率流计算结果的影响；最后研究三维耦合梁结构功率流的主动控制，分别从频域和空间域验证功率流主动控制方法的正确性与有效性，并分析最优控制力微小偏差和误差传感器位置对控制效果的影响。

3.1 动力学响应仿真算例与分析

如图2所示的悬臂三维耦合梁结构，其由三根空间梁单元相互垂直连接，三根梁的结构尺寸和材料参数相同。结构尺寸长度L=2 m，梁截面为圆形，且直径D=0.02 m；材料参数弹性模量E=2.0×1011N/m2，密度ρ=7 800 kg/m3，泊松比ν=0.3，阻尼因子η=0.001；扰动力F0eiωt(F0=1 N)作用于2梁x0=1 m位置；控制力Fseiωt作用于2梁xs=1.2 m位置；而误差传感器位于3梁xe=0.8 m位置。其仿真结果如下：

图3给出了扰动力F0eiωt作用于2梁x0=1 m位置时，1梁中点位置处Y方向位移频响函数的行波解及将结构分别划分为120、180、240梁单元的有限元解。在有限元方法计算中，当分析频率为2 000 Hz时，选取的最长单元长度Δ=L/40=0.05 m<λmin/4=0.07 m(λmin为最小波长)，满足由频率范围上限来确定有限元网格划分的细化标准，保证了有限元方法的计算精度。图4为分别基于Timoshenko梁理论与Euler-Bernoulli经典梁理论计算3梁中点位置处的主动功率流对比图。图5给出了不同位置处包含纵波和扭转波的总功率流和仅考虑弯曲波的功率流的对比结果，以此说明纵波和扭转波对三维耦合梁结构功率流计算结果的影响。

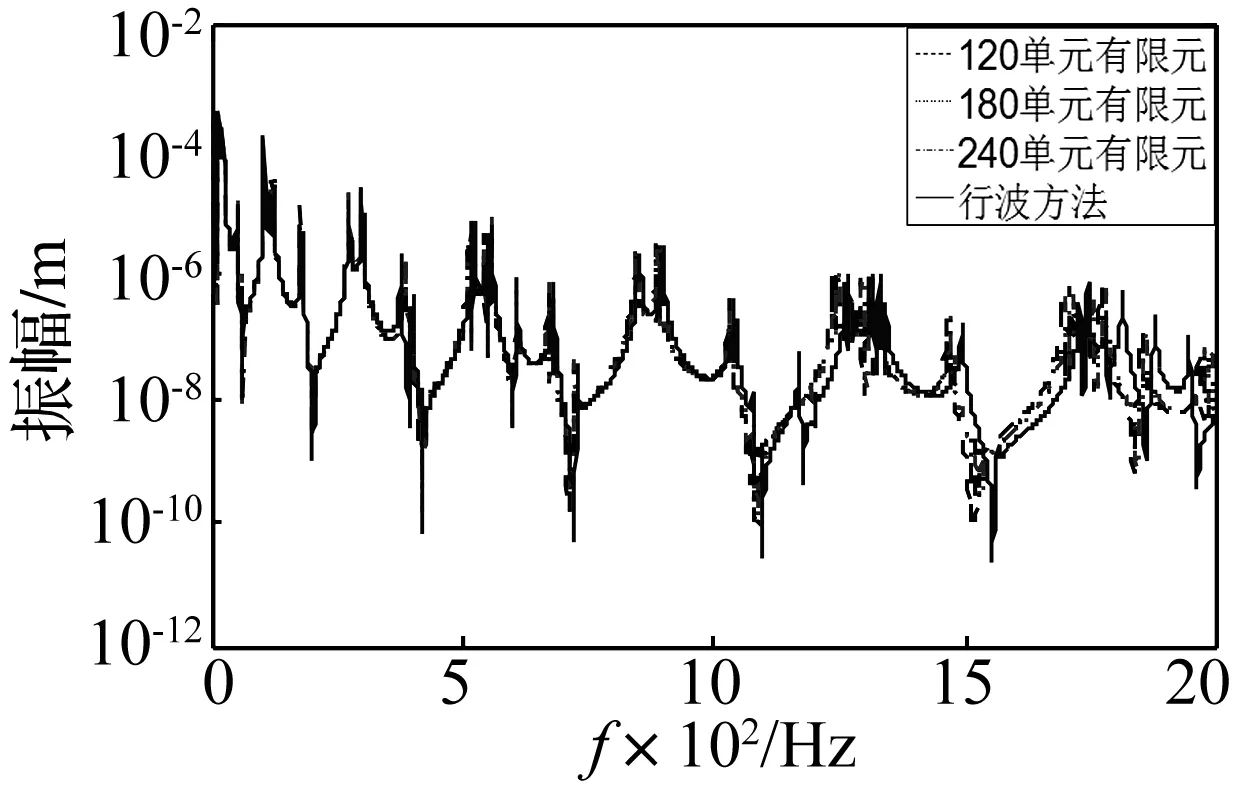
图3 有限元与行波方法计算三维耦合梁结构动力学响应

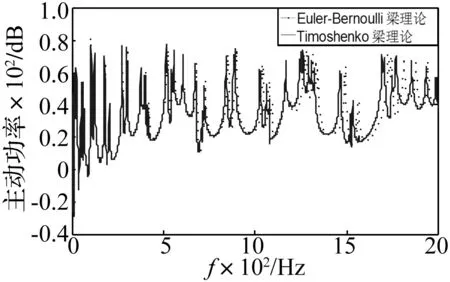
图4 Timoshenko梁理论与Euler-Bernoulli梁理论计算结构中的主动功率流(dB ref：10-10w)

(a) 2梁x=1.4 m (b) 1梁中点 (c) 3梁中点

从图3中可以看出：基于模态叠加的有限元法计算结果在低频段与行波方法计算结果很吻合。在中高频段，随着单元的增加，有限元法的解逐渐趋向于行波解。造成这种差别的原因在于有限元采用模态叠加方法计算结构响应，在求解过程中存在截断误差，且高阶模态计算不准确；而行波方法不受模态的限制，因而可以精确计算结构在全频域下的响应。

由图4可得：两种梁理论计算三维耦合梁结构中主动功率流的结果是不同的，Timoshenko梁理论计算的共振频率要明显低于Euler-Bernoulli梁理论计算的结果。其原因为：在Euler-Bernoulli梁理论中，没有考虑结构剪切变形的影响，梁的剪切刚度是被认为是无穷大，然而，梁的实际剪切刚度是有限的。Timoshenko梁理论考虑了剪切变形和转动惯量的影响，其不仅在高频段，而且在中、低频段影响了梁结构的功率流传播，使其计算的共振频率要低于Euler-Bernoulli理论结果，而且其结果更接近于真实梁结构的动态特性。

图5给出了不同响应位置处总功率流与仅考虑弯曲波的功率流的对比。从图中可以看出，随着分析频率的升高和响应位置与扰动位置距离的增加，两者结果的差异变大。这是因为在三维耦合结点处存在弯曲波、纵波与扭转波相互之间的转换，即使横向扰动力作用于结构，通过耦合结点也会产生纵波与扭转波，且纵波与扭转波的影响随频率升高而不断增大。因此，在分析三维耦合梁结构中传播的功率流时，需包含纵波与扭转波的影响，否则在进行复杂结构分析时，将会产生较大的误差。

3.2 功率流主动控制仿真算例

针对图2所示的悬臂三维耦合梁结构进行功率流主动控制仿真，其初始条件同3.1节。图6和8分别为功率流主动控制在频域与空间域的控制效果对比图，在图7中给出了最优控制力微偏差的影响。图9研究了不同误差传感器位置对功率流主动控制效果的影响。

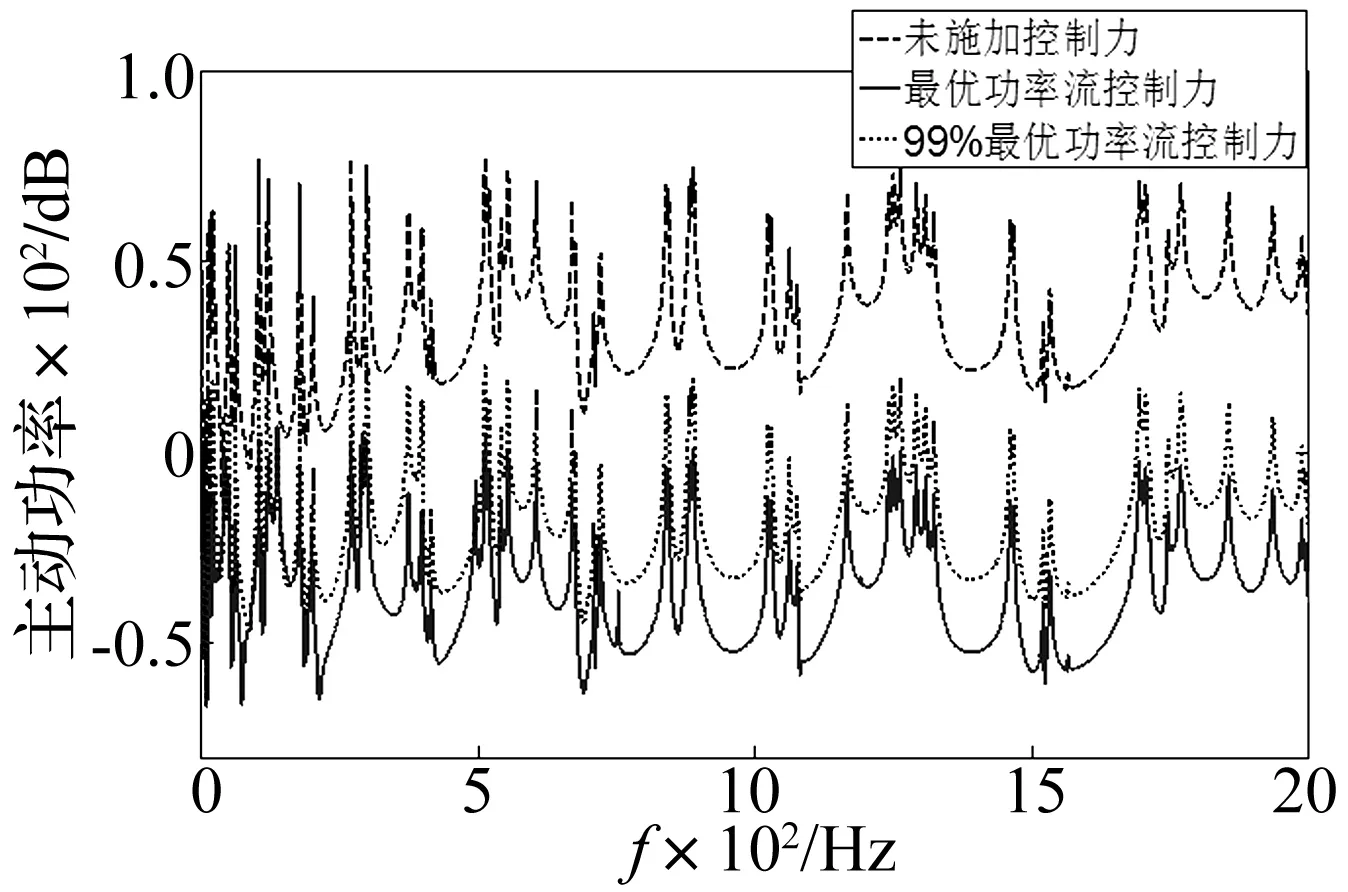
图6 3梁中点截面位置处控制前后的频域功率流对比(dB ref：10-10w)

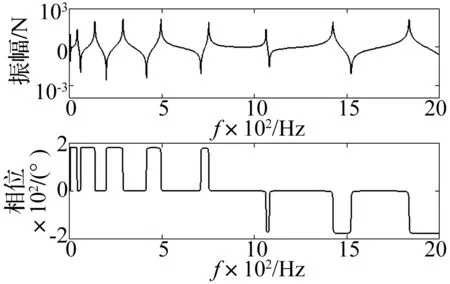
图7 功率流主动控制下的最优控制力

图6和图8分别为三维耦合梁结构功率流主动控制在频域和空间域的控制效果图，图7为功率流主动控制的最优控制力图。从图6中可以看出：采用功率流主动控制方法可以明显降低三维耦合梁结构中传播的功率流，且在全频域中功率流平均衰减了大约70 dB，1%的最优控制力偏差对控制效果的影响甚微。由功率流优化可以得到如图7所示的控制力，控制通过前馈自适应算法可以实现结构振动功率流传递的抑制。图8给出了三维耦合梁结构在低、中、高频域下定频激励结构空间域的控制效果。从图中可以得出：通过施加最优控制力，1、2、3梁单元中传播的主动功率流得到了有效控制；且扰动力与控制力的作用将引起结构功率流传递的不连续，由2梁仿真结果可以得到在控制力作用的下游位置，功率流的衰减较为明显。综上所述，功率流主动控制方法可以实现三维耦合梁结构全频域整体振动的抑制。

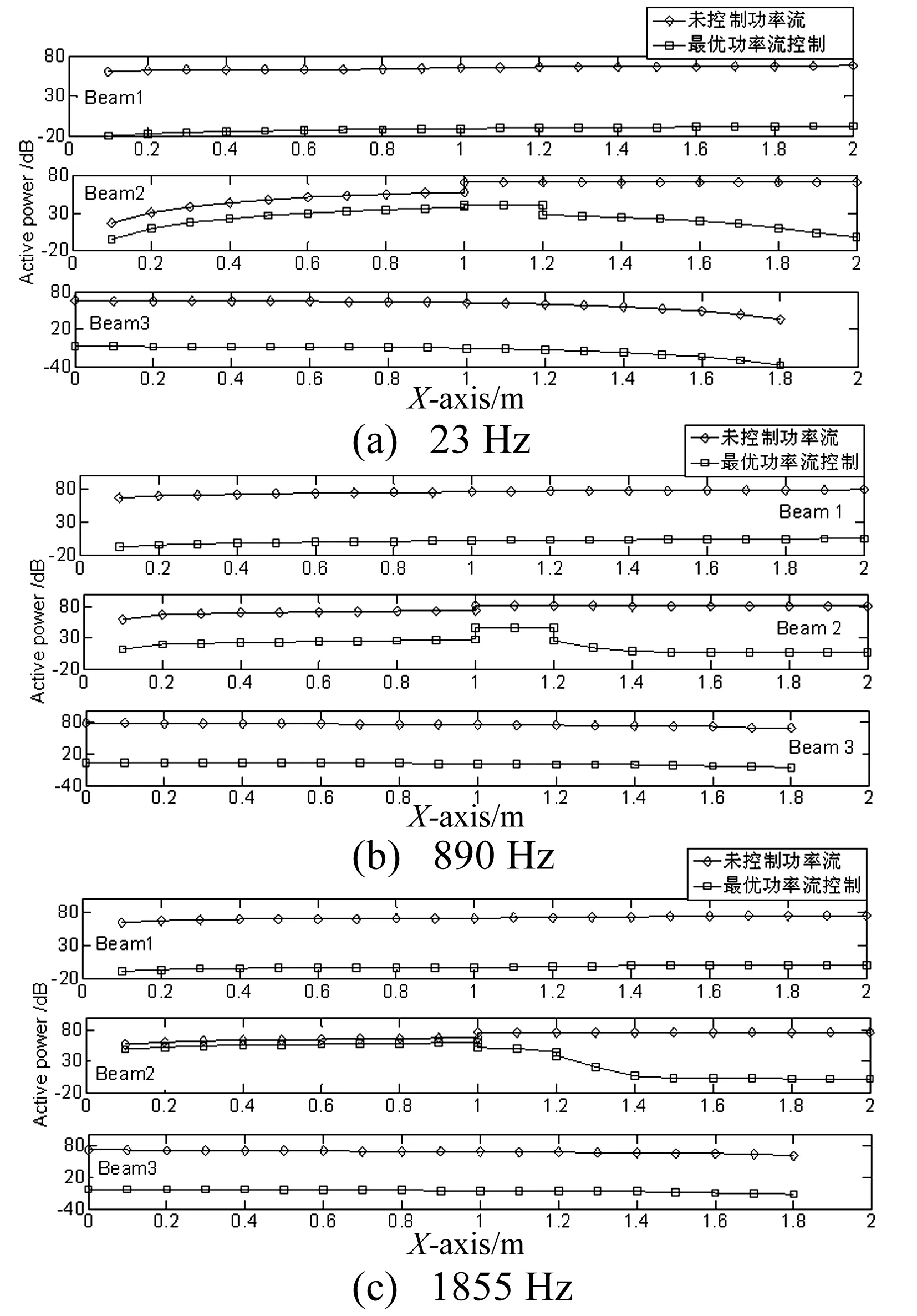
图8 不同频率空间域中控制前后的功率流对比 (dB ref：10-10w)

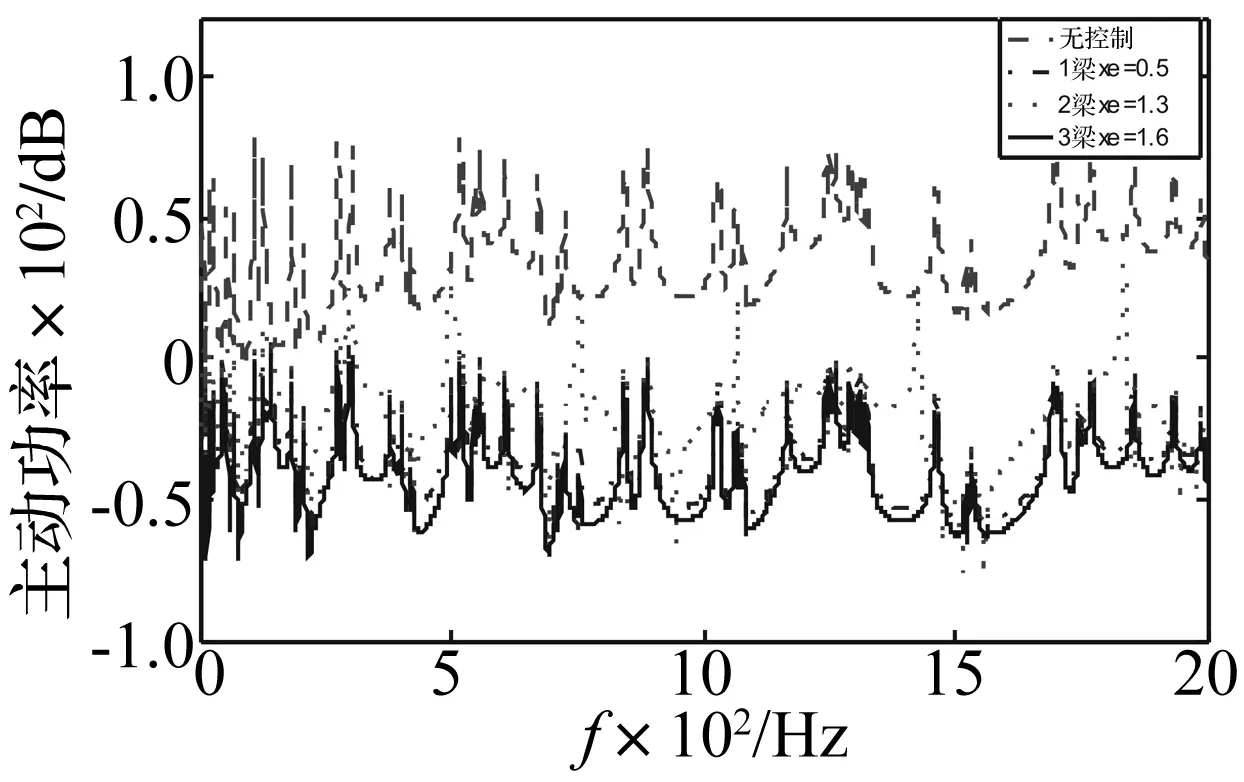
图9 误差传感器不同位置处的功率流

图9为误差传感器位于控制力近场或远场情况下功率流主动控制的控制效果。从图中可以看出：无论误差传感器位于控制力的近场或远场，功率流主动控制方法都可以很好地实现三维耦合梁结构全频域下振动的控制[7]。

4 结 论

本文基于行波方法对三维耦合Timoshenko梁结构中的功率流传播与主动控制进行了深入研究。其主要结论有：

(1) 行波方法可以精确计算三维耦合梁结构全频域下的动力学响应。

(2) 通过Timoshenko梁理论与Euler-Bernoulli经典梁理论计算结果对比可知：Timoshenko理论考虑了剪切变形和转动惯量的影响，能更为完整地反映梁结构的动力学特性。在中高频域其分析结果更为精确，并且更接近于工程实际。

(3) 由于三维耦合梁结构结点处存在弯曲波、纵波与扭转波之间的相互转换，因此在进行三维耦合梁结构的主动功率流计算时，为获得更为真实和精确的结果，需同时考虑弯曲波、纵波与扭转波对结构主动功率流的贡献。

(4) 通过上述理论分析与数值计算可得：功率流主动控制可以克服传统方法中高频控制受限，不能有效控制中高频扰动的缺点和不足，实现了三维耦合梁结构全频域下整体振动的抑制，并且最优控制力的微小偏差和误差传感器的位置对功率流主动控制效果影响甚微。

本文基于Timoshenko梁理论给出了三维耦合梁结构的精确动力学模型与功率流主动控制方法，其研究成果可以进一步应用到复杂空间桁架结构的动力学分析与振动控制研究中。

[1]庞世伟, 杨雷, 曲广吉. 高精度航天器微振动建模与评估技术最近进展 [J]. 强度与环境, 2007, 34 (6): 1-9.

PANG Shi-wei, YANG Lei, QU Guang-ji. New development of micro-vibration integrated modeling and assessment technology for high performance spacecraft [J]. Structure & Environment Engineering, 2007, 34 (6): 1-9.

[2]Miller D W, Von Flotow A. A travelling wave approach to power flow in structural networks [J]. Journal of Sound and Vibration, 1989, 128(1): 145-162.

[3]Goyder H G D, White R G. Vibrational power flow from machines into built-up structures. Part I. Introduction and approximate analyses of beam and plate-like foundations [J]. Journal of Sound and Vibration, 1980, 68 (1):59-75.

[4]Pan J, Hansen C H. Active control of total vibratory power flow in a beam. I: Physical system analysis [J]. The Journal of the Acoustical Society of America, 1991, 89(1): 200-209.

[5]Schwenk A E, Sommerfeldt S D, Hayek S I. Adaptive control of structural intensity associated with bending waves in a beam[J]. The Journal of the Acoustical Society of America, 1994, 96(5): 2826-2835.

[6]Pereira A K A, Moreiraf F J O, Arruda J R F. Active control of the structural intensity in beams using a frequency domain adaptive method [J]. AIAA-1998-1798: 841-849.

[7]Audrain P, Masson P, Berry A. Investigation of active structural intensity control in finite beams: theory and experiment [J]. The Journal of the Acoustical Society of America, 2000, 108(2): 612-623.

[8]Liu Chun-chuan, Li Feng-ming, Huang Wen-hu. Active vibration control of finite L-Shaped beam with travelling wave approach [J]. Acta Mechanica Solida Sinica, 2010, 23(5): 377-385.

[9]朱宏平，徐荣光. 基于功率流的结构主动控制方法 [J]. 振动与噪声控制，1998(5): 21-28.

ZHU Hong-ping, XU Rong-guang. Based on the power flow in active structural control method [J]. Journal of Vibration and Noise Control, 1998(5):21-28.

[10]宋孔杰，张蔚波，牛军川. 功率流理论在柔性振动控制技术中的应用与发展 [J]. 机械工程学报，2003，39(9):23-28.

SONG Kong-jie, ZHANG Wei-bo, NIU Jun-chuan. Application and development of power flow theories in the field of the vibration control for flexible systems [J]. Chinese Journal of Mechanical Engineering, 2003, 39(9): 23-28.

[11]伍先俊，朱石坚. 振动反馈主动控制的功率流计算方法研究 [J]. 船舶力学，2009，13(2): 298-304.

WU Xian-jun, ZHU Shi-jian. A method to calculate the vibration power flow in the feedback vibration control system [J]. Journal of Ship Mechanics, 2009, 13(2): 298-304.

[12]金全洲，李天匀，赵耀，等. 圆柱壳结构振动功率流和主动力幅值的控制研究 [J]. 船舶力学，2009，13(2): 305-312.

JIN Quan-zhou, LI Tian-yun, ZHAO Yao, et al. Active control of cylindrical shells based on structure power flow and control inputs [J]. Journal of Ship Mechanics, 2009, 13(2): 305-312.

[13]陈荣，孙玲玲，吴银兵，等. 基于Timoshenko梁理论的斜置系统功率流特性分析 [J].振动与冲击, 2010, 29(9): 97-101.

CHEN Rong, SUN Ling-ling, WU Yin-bing, et al. Power flow analysis of inclined isolation system based on viscoelastic fractional derivative model [J]. Journal of Vibration and Shock, 2010, 29(9):97-101.

[14]Beale L S, Accorsi M L. Power flow in two-and three-dimensional frame structures [J]. Journal of Sound and Vibration, 1995, 185(4):685-702.

[15]王有懿，马文来，赵阳. Timoshenko梁功率流主动控制研究[J]. 振动与冲击，2013, 32(7):102-106.

WANG You-yi, MA Wen-lai, ZHAO Yang. Active control for power flow of a Timoshenko beam [J]. Journal of Vibration and Shock, 2013, 32(7):102-106.