含间隙曲柄滑块系统动力响应的随机性分析

赵 宽, 陈建军, 曹鸿钧, 云永琥

(西安电子科技大学 电子装备结构设计教育部重点实验室，西安 710071)

在机构多体系统中，由于装配误差、摩擦磨损以及机构运动的需要，运动副间隙是不可避免的，这将导致机构的实际运动与理想运动之间出现偏差，且在运动过程中运动副会因间隙的存在出现瞬间失去接触，待再接触时将产生碰撞，从而引起振动、产生噪音、加速磨损，甚至会严重影响系统的动态性能，降低系统的运动精度、稳定性、可靠性以及使用寿命[1]。另一方面，由于制造、装配、摩擦、冲击、温变等因素，将使包含间隙在内的机构系统的几何参数和物理参数都具有一定的随机性，综合考虑这些随机因素下的系统响应，将使分析结果更接近工程实际，同时也为含间隙系统的可靠性分析及优化设计奠定了基础。

目前，国内外对关节间隙所带来的动力学现象以及优化、控制等方面开展了许多研究工作。文献[2]分别对含间隙铰和润滑铰的机构系统进行了动力学研究，数值仿真表明接触碰撞力对含间隙铰系统的动力学特性有较大的影响，而润滑铰和理想铰的性能十分接近。文献[3]分别对含间隙和润滑球铰的空间柔性多体系统进行动力学分析。文献[4]利用遗传算法对含间隙铰的曲柄滑块机构的传动角进行优化。文献[5]基于Pyragas方法对含间隙铰的曲柄滑块机构进行稳定性分析。但在以上文献的模型中是将所有参数和作用载荷均视为确定性量或参数，而实际上在随机因素的作用下这些参数的取值可能呈现出某种程度的随机性。对含有间隙的精密机械系统，参数的随机性对系统动力特性的影响是不容忽视的。文献[6-7]对无间隙的不确定参数弹性连杆机构的动力响应进行了分析。然而，对于含有间隙和摩擦的随机参数多体系统的动力学分析研究却鲜有报道。

本文基于以上研究成果，建立了含间隙和摩擦的曲柄滑块系统的动力学模型，同时综合考虑系统物理参数和几何参数的随机性，利用BP人工神经网络的函数逼近能力，建立起系统基本随机变量和系统动力响应间的映射关系，利用矩法获得了各响应量的均值和均方差随时间的变化规律，考察了系统各随机参数对系统动力响应的影响，并通过Monte-Carlo(MC)模拟法对计算结果进行验证，得出了一些有意义的结论。

1 曲柄滑块系统运动的随机性分析

图1为曲柄滑块系统理想模型的示意图，曲柄AB和连杆BC的长度分别为L1和L2，曲柄以角速度ω绕支点A匀速转动，则滑块的位移xC可表为：

(1)

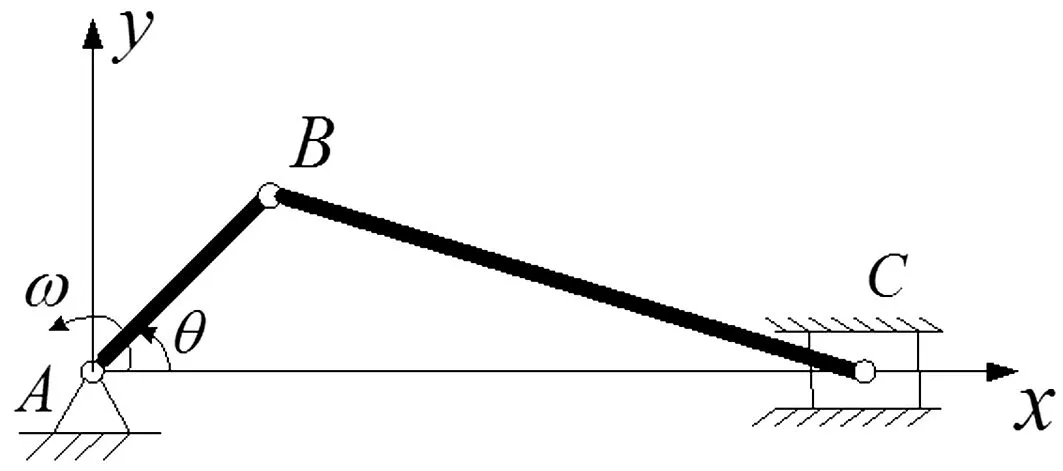
图1 曲柄滑块系统

设几何参数L1和L2为相互独立且服从正态分布的随机变量，对上式利用矩法[8]可求得滑块C在任意时刻位移xC的均值μC和均方差σC分别为：

(2)

(3)

式中，μL1和μL2分别为L1和L2的均值，σL1和σL2分别为L1和L2的均方差。

将式(1)对时间求导，同理可求出滑块C的速度和加速度的均值和均方差。

2 含间隙曲柄滑块系统的动力学建模

2.1 间隙旋转铰模型

由于旋转铰间隙的存在，使得系统成为变拓扑结构系统，一种是不含约束的自由运动；另一种是具有单边约束的运动。目前处理铰间隙问题主要有三种模型，一是无质量刚性杆模型，该模型无法考虑接触时的冲击效应，难以描述运动副间的动力特性以及碰撞对系统动力学的影响；二是等效弹簧阻尼模型，该模型难以描述碰撞过程中能量转移的物理本质。为此，本文采用了第三种模型，将间隙铰视为两个弹性碰撞体，即图2所示的旋转铰模型，设轴承和轴颈的半径分别为rB和rJ，中心距为r，则间隙大小为：

rc=rB-rJ

(4)

轴承和轴颈接触点的法向穿透深度为：

δBJ=r-rc

(5)

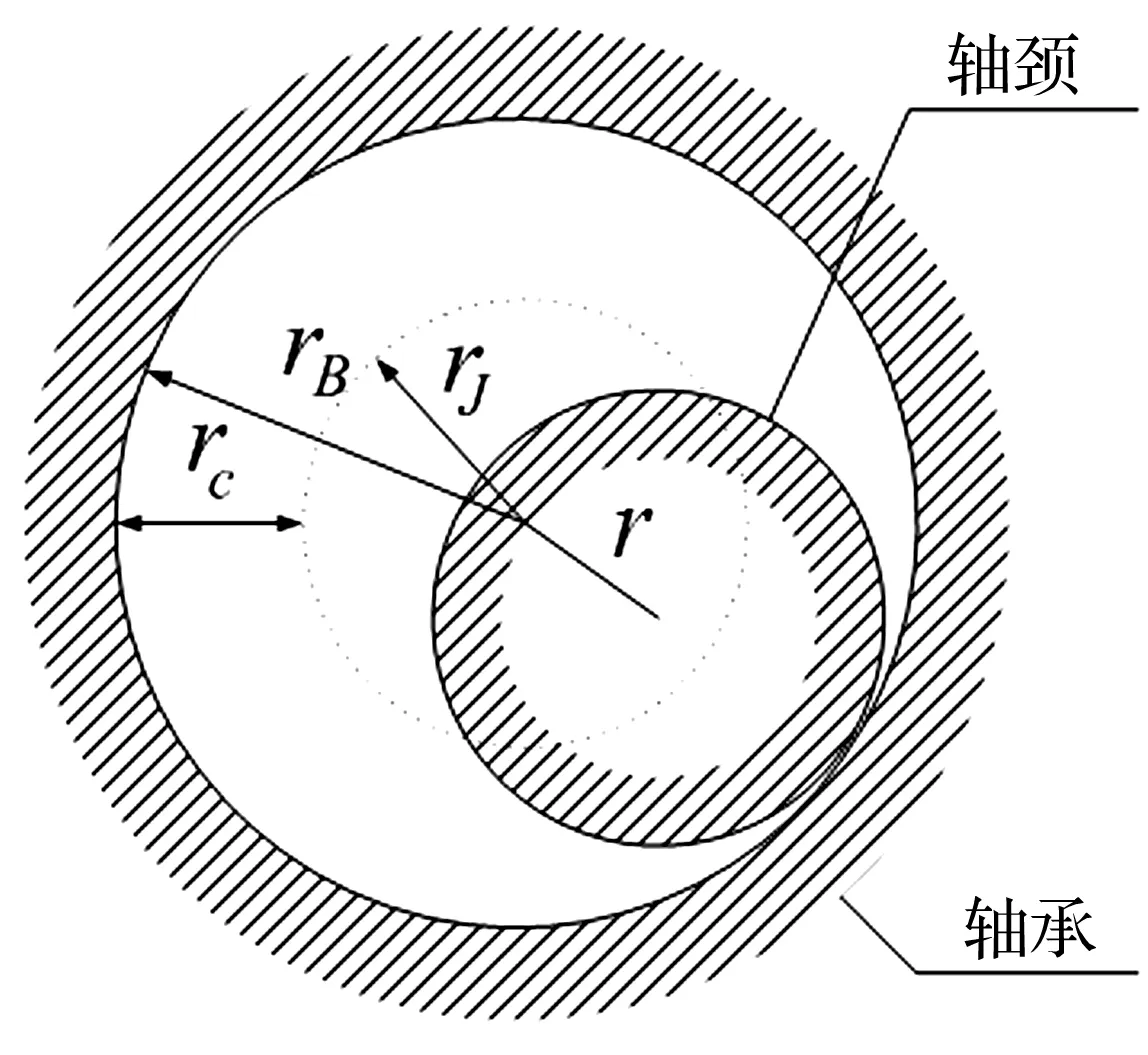
图2 间隙旋转铰

目前，对于描述铰间隙处碰撞接触过程中力与位移之间的关系，最常用的有Hertz接触力模型和Lankarani与Nikravesh提出的连续接触力模型，前者是一种纯弹性碰撞模型，不考虑碰撞过程中的能量损失，主要用于早期的碰撞问题；后者不仅考虑碰撞接触速度、构件的材料属性以及碰撞体的几何特性等因素，而且有利于系统动力学方程的稳定求解，因此得到了广泛的应用。故本文采用了后者，则轴承和轴颈法向接触力Fn可表为[9]：

(6)

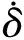
(7)

当两间隙物体接触后，由于切向摩擦力的作用会发生相对滑动或粘滞，进一步影响到整个间隙系统的运动和动力响应，因此有必要考虑摩擦力对系统动力响应的影响。对铰间隙碰撞接触处采用了Ambrosio提出的Coulomb摩擦模型，切向摩擦力的表达式为[11]：

(8)

式中，cd为动态修正系数；cf为动摩擦因数；vT为相对切向速度。

2.2 系统动力学模型

(9)

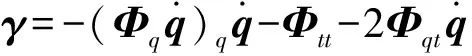
该方程综合了旋转间隙铰脱离接触自由运动和接触碰撞两个阶段的运动模式，有利于实现系统整个运动过程的动力学仿真。

3 含间隙曲柄滑块系统动力响应的随机性分析

方程(9)为确定性系统的分析模型。现考虑系统具有随机性的情况，假设含间隙曲柄滑块系统中共有m0个相互独立的服从正态分布的随机参数，将这些随机参数代入式(9)中，则系统模型成为含随机参数的不确定性模型。由于含间隙的曲柄滑块是一个变结构、含碰撞、非定常、且非线性很强的系统，利用传统的算法难以对其进行随机性分析，而神经网络法较多项式响应面法具有更高的稳定性和更好的精度[13]，因此，本文利用该方法获得系统随机参数和动力响应的近似函数关系式以及系统动力响应对各随机参数的灵敏度，然后应用矩法对系统的动力响应进行随机性分析。

3.1 BP神经网络法

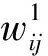
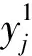
(10)

(11)

(12)

式中fi(·)(i=1,2)为传递函数。

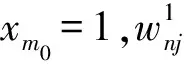
3.2 系统动力响应的随机性分析

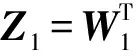
(13)

式中Y(X)=[y1(X),y2(X),…,ym3(X)]。

由于系统动力响应的随机性分析中需要系统动力响应的导数，即系统动力响应对各随机参数的灵敏度，由复合函数的求导法则可得：

(14)

其中yl(l=1,2,…,m3)表示第l个系统动力响应，由矩法可得yl的均值和均方差分别为：

μyl=yl(μX)

(15)

(16)

综合以上分析过程，给出利用BP神经网络对含间隙和摩擦的曲柄滑块系统随机性分析的具体步骤如下：

(1) 选取广义坐标，建立式(9)所示的系统动力学模型，具体建模和编程过程可参考文献[12]和[14];

(2) 确定系统随机输入参数的分布类型，随机抽取50组输入参数，采用自适应4阶龙哥库塔算法求出与输入随机参数X相对应的系统动力响应Y；

(3) 以数据{X,Y}为学习训练样本，利用Levenberg-Marquardt法[7]对图3所示的神经网络进行训练，得到系统动力响应的近似表达式，再由式(14)得到系统动力响应对各随机参数的灵敏度；

(4) 利用式(15)和(16)求出系统动力响应的均值和均方差。

4 数值算例

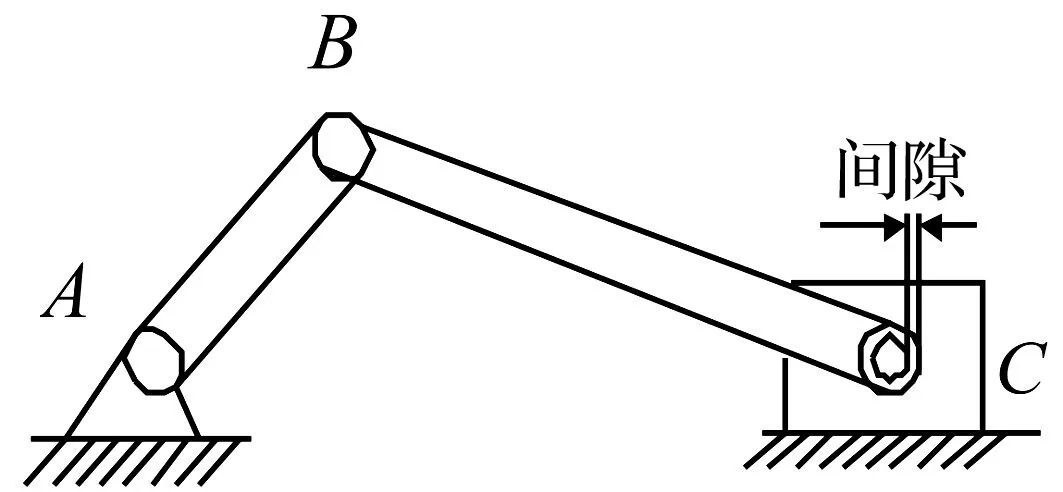
图4 含间隙的曲柄滑块系统

考虑间隙和摩擦的随机参数曲柄滑块系统如图4所示，其中点A、B两处为理想铰，点C处为间隙铰。曲柄以转速150 r/min定轴旋转，滑块的质量为0.14 kg，取轴承和轴颈碰撞过程中的能量恢复系数ce为0.95。现考虑系统中曲柄和连杆的两者的弹性模量E、长度Li(i=1,2)、质量mi(i=1,2)、转动惯量Ii(i=1,2)，以及轴承和轴颈的半径rB和rJ、轴承和轴颈的滑动摩擦系数cf等均为相互独立的正态分布随机参数，它们的均值见表1。借助Matlab神经网络工具箱编制程序，选取步长为10-6s，针对无间隙和摩擦的理想模型及含间隙和摩擦的间隙模型两种情况，对一个周期内系统动力响应的随机性进行分析，并将计算结果以时间历程图的方式给出。

表1 系统构件尺寸及物理参数的均值

图5、图6分别给出了理想模型和考虑间隙的确定性模型其滑块速度响应和加速度响应的时间历程图。图7、图9给出了系统各参数的变异系数均取0.01时滑块速度均值和加速度均值在随机参数理想模型和含间隙模型中随时间变化的对比曲线。图8、图10给出了系统各随机参数的变异系数均取0.01时滑块速度均方差和加速度均方差在随机参数理想模型和含间隙模型中随时间变化的对比曲线。从这些图中显见：① 在确定性理想模型中，滑块的速度和加速度响应是平滑的，而间隙模型中则有较大的波动，原因是在系统运动过程中，由于铰间间隙和摩擦的存在，使得轴承和轴颈间发生从不接触到接触碰撞、再到不接触的连续循环状态，这与文献[5]的计算结果相近，说明计算结果的正确性；② 滑块速度和加速度的均值出现震荡现象，这是由系统参数的随机性使得间隙处接触碰撞的时间发生微小改变而引起的；③ 与不考虑间隙和摩擦的随机理想模型相比，含间隙模型中滑块速度和加速度的均方差偏大，这有可能造成整个系统的功能失效或破坏，因此有必要就各随机参数对系统动力响应的影响进行分析，从中找出关键参数以提高系统运动功能的可靠性。

为了考察各随机参数的分散性对系统动力响应的影响，表2列出了在0.01 s时刻所有随机参数的变异系数vall均取0(确定性模型)和0.01，以及同种类随机参数的变异系数取0.01，而其余为0时滑块位移、速度和加速度均值和均方差的计算结果，表中第4行为Monte-Carlo(MC)法模拟1 000次的结果。对表中结果分析可见：① 本文方法的结果与MC法模拟的结果两者吻合较好，表明该方法的可行性； ② 与确定性模型相比，随机模型中参数的随机性对滑块位移和速度的影响不大，但对加速度的影响较大；③ 在诸随机参数中，弹性模量对系统动力响应随机性的影响最小，转动惯量次之，而间隙的影响最大。

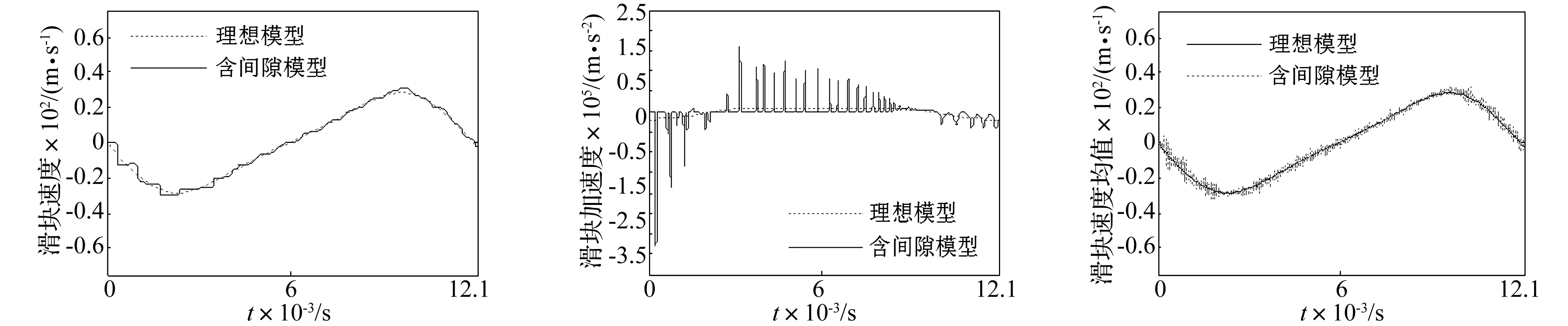
图5 滑块速度的响应时程

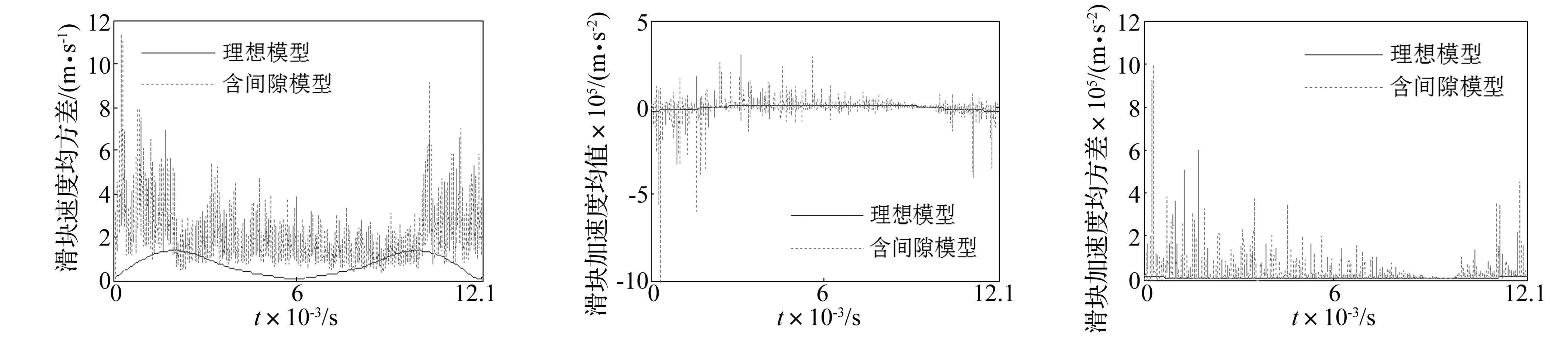
图8 滑块速度均方差的时间历程图

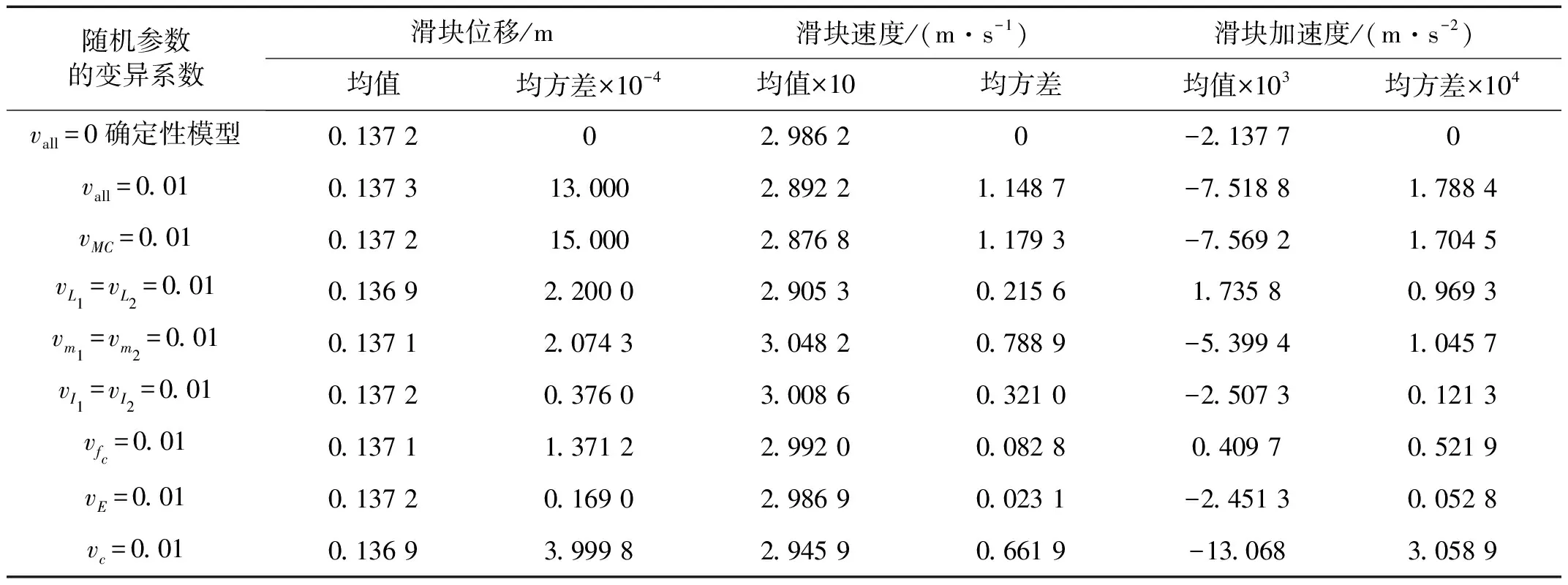
表2 不同随机参数对系统动力响应数字特征的影响

5 结 论

文中在考虑铰间摩擦以及系统参数具有随机性的情况下，对含间隙的曲柄滑块系统其动力响应问题进行了分析。建立了系统的动力学模型，将BP神经网络法拓展应用于含间隙及摩擦的曲柄滑块系统的随机性分析中，通过算例验证了文中模型和方法的合理性和正确性，并得出以下结论：① 通过与MC法计算结果的对比表明，本文方法可行且具有一定的精度；② 系统参数的随机性将有可能增强系统间隙处的碰撞，使系统动力响应的分散性增大；③ 系统参数的随机性对含间隙系统动力响应的影响不容忽略，其中间隙的随机性对系统动力响应分散性的影响最大。故欲提高系统的动力学性能，应首先降低该参数的分散性。

[1]Erkaya S, Uzmay I. Experimental investigation of joint clearance effects on the dynamics of a slider crank mechanism[J]. Multibody System Dynamics, 2010, 24(1): 81-102.

[2]Flores P, Amrosio J, Claro J C P, et al. A study on dynamics of mechanical systems including joints with clearance and lubrication[J]. Mechanism and Machine Theory, 2006, 41(3): 247-261.

[3]TIAN Qiang, ZHANG Yun-qing, CHEN Li-ping, et al. Dynamics of spatial flexible multibody systems with clearance and lubricated spherical joints[J]. Computers and Structures, 2009, 87(13-14): 913-929.

[4]Erkaya S, Uzmay I. Optimization of transmission angle for slider-crank mechanism with joint clearance[J]. Struct Multidisc Optim, 2009, 37(5): 493-508.

[5]Olyaei A A, Ghazavi M R. Stabilizing slider-crank mechanism with clearance joints[J]. Mechanism and Machine Theory, 2012, 53: 17-29.

[6]魏永祥, 陈建军, 马洪波，等. 随机参数弹性连杆在平稳随机激励下的动力可靠性分析[J]. 机械工程学报, 2012, 48(2): 36-43.

WEI Yong-xiang, CHEN Jian-jun, MA Hong-bo, et al. Dynamic reliability analysis of elastic linkage mechanism with stochastic parameters under stationary random excitation[J]. Journal of Mechanical Engineering, 2012, 48(2): 36-43.

[7]拓耀飞, 陈建军, 陈永琴，等. 基于神经网络的弹性连杆机构动力响应分析[J]. 西安电子科技大学学报, 2006, 33(5): 711-715.

TUO Yao-fei, CHEN Jian-jun, CHEN Yong-qin, et al. Dynamic analysis of the elastic linkage mechanism based on the artificial neutral network[J]. Journal of Xidian University, 2006, 33(5): 711-715.

[8]陈建军. 机械与结构系统的可靠性[M]. 西安: 西安电子科技大学出版社, 1995.

[9]Lankarani H M, Nikravesh P E. A contact force model with hysteresis damping for impact analysis of multibody systems[J]. Journal Mechancal Design, 1990, 112(3): 369-376.

[10]Dubowsky S, Freudenstein F. Dynamic analysis of mechanical systems with clearances, part 1: formation of dynamic model[J]. Journal of Engineering for Industry, 1971, 93(1): 305-309.

[11]Flores P. Dynamic analysis of mechanical systems with imperfect kinematic joint[D]. University of Minho, Guimaraes, Portugal, 2005.

[12]Flores P, Ambrosio J. On the contact detection for contact-impact analysis in multibody systems[J]. Multibody System Dynamics, 2010, 24(1): 103-122.

[13]段巍, 王璋奇. 利用响应面方法的汽轮机叶片振动可靠性分析[J]. 振动、测试与诊断, 2012, 32(1): 84-90.

DUAN Wei, WANG Zhang-qi. Vibration reliability of turbine blade based on response surface method[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(1): 84-90.

[14]Nikravesh P E. Computer aided analysis of mechanical systems[M]. Prentice Hall, Englewood Cliffs, New Jersey, 1988.