考虑火灾全过程的钢管混凝土平面框架受力性能分析

王景玄，王文达

(兰州理工大学 甘肃省土木工程防灾减灾重点实验室，兰州 730050)

近年来由于建筑火灾的频发和钢管混凝土结构广泛应用于各种多高层民用建筑和工业建筑中[1]，深入研究其耐火性能和抗火设计方法具有重要的理论与应用价值。目前，对于钢管混凝土构件的抗火试验及理论研究较多，而节点和框架的研究相对较少。如Schaumamn等[2]进行了高强钢管内填充高强混凝土柱耐火极限研究；任晓虎等[3]进行了火灾下钢管混凝土梁落锤冲击试验研究；Yang等[4]对钢管混凝土轴压柱受火性能进行了理论分析；Song等[5]分析了钢管混凝土短柱在经历常温加载、升温、降温以及火灾后不同阶段的力学性能；Huo等[6]进行了8个有初始荷载作用的钢管混凝土柱经历火灾全过程的滞回试验研究。Tao等[7]进行了64根受火的钢管混凝土柱和12根未受火的钢管混凝土柱钢管和核心混凝土粘结滑移性能试验研究；霍静思等[8]进行了标准火灾下钢管混凝土短柱落锤冲击试验研究。Wang等[9]进行了矩形钢管混凝土柱-外伸端板连接钢梁节点的耐火性能研究；Ding等[10]进行了7榀方钢管混凝土柱-组合梁子框架部件模型的耐火试验；Song等[11]介绍了钢管混凝土柱-钢梁组合节点在考虑荷载与温度共同作用下的试验与理论研究；Tan等[12]对钢管混凝土柱-钢筋混凝土梁组合节点耐火性能和破坏机制进行了分析。Han等[13]介绍了6榀钢管混凝土柱-钢筋混凝土梁平面框架耐火性能试验研究，基于此试验，Han等[14]进行了该类框架耐火性能的数值模拟和参数分析；王景玄等[15]进行了考虑火灾全过程的钢管混凝土柱-钢梁平面框架温度场计算和力学性能的初步分析。

目前对于考虑火灾全过程作用的钢管混凝土柱-钢梁平面框架抗火试验研究还未见报道。因此，本文通过数值模拟，对经历常温加载、恒载升温、降温以及火灾后继续加载等受火全过程作用的钢管混凝土柱-组合梁平面框架的受火机理和受力性能进行分析研究，并进行相应的参数分析，了解该类结构在不同参数下的工作机理，以期为考虑火灾全过程作用的钢管混凝土组合框架性能研究提供参考。

1 有限元模型

1.1 热传模型

在温度场模型中，钢管、核心混凝土、钢梁、栓钉以及RC板均采用八节点三维实体单元DC3D8，以便考虑温度梯度效应；钢筋采用二节点杆单元DC1D2。钢管和混凝土构件、钢梁和RC板之间采用绑定约束(Tie)，即不考虑相对滑移。钢筋和RC楼板之间采用约束方程(Equation)建立接触关系。在输入文件(*.inp)里写入命令“NODE FILE, ENTER NT”语句，生成(*.fil)文件，实现热传模型与力学模型的顺序耦合。计算时考虑钢材和混凝土膨胀热应变影响，由于混凝土高温徐变与热膨胀应变相比，绝对值约小一个数量级，故不考虑混凝土高温徐变和瞬态热应变等影响[11]。

1.2 力学模型

考虑火灾全过程作用的钢管混凝土柱-组合梁平面框架力学模型中，合理选取火灾全过程每个阶段的材性是至关重要的。韩林海[1]中归纳了常温、升温、自然冷却火灾后钢材与考虑钢管约束效应核心混凝土的材料本构关系，并且通过大量试验验证。本文选用Song等[5]中钢材降温段的材性，假定钢材在弹性段和强化段材性都有所恢复，其应力-应变关系表达式如下：

(1)

式中：T为当前温度；Tmax为历史最高温度；T0为环境温度，取20℃；

fyc(T,Tmax)=fyh(Tmax)-

为降温过程中钢材的屈服强度；

εyc(T,Tmax)=εyh(Tmax)-

为降温过程中钢材的屈服应变；

为降温段的弹性模量。

降温段混凝土材料本构关系假定与当前温度无关，只考虑历史最高温度的影响，故采用高温后核心混凝土的应力-应变关系模型[1]。对于钢筋混凝土楼板中普通混凝土材性按吴波[16]选取。

此外，材料的热膨胀效应对受火计算影响较大，本文通过热膨胀系数反映升温段和降温段材料的温度变形，其计算公式如式(2)和(3)所示，式中αs为钢材的热膨胀系数，αc为混凝土的热膨胀系数。

(2)

αc=(0.008T+6)×10-6m/(m·℃)

(3)

在力学模型中准确调用每个阶段的材性是火灾全过程计算的核心和关键问题。为了更清楚了解整个受火阶段计算过程，图1给出了其分析流程。

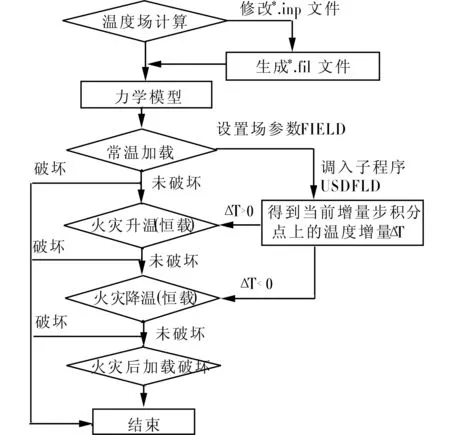
图1 分析流程

王景玄[17]给出了考虑火灾全过程的钢管混凝土柱-组合梁框架力学有限元模型的具体建模方法和不同受火阶段材性的具体调用方法。有限元模型网格划分以及边界条件如图2所示，以方截面柱钢管混凝土柱-组合梁平面框架为例。

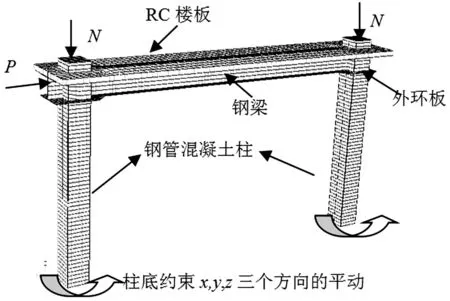
图2 网格划分及加载边界条件

2 算例分析

2.1 模型验证

由于目前没有公开关于考虑火灾全过程的钢管混凝土柱-组合梁平面框架的抗火试验数据，为验证模型的正确性，分别选择已有研究者完成的考虑火灾全过程作用的钢管混凝土柱、钢管混凝土组合节点试验和钢管混凝土柱-钢筋混凝土梁平面框架耐火试验结果对比验证。

采用Huo等[6]中火灾全过程作用钢管混凝土柱滞回性能试验模型进行分析。试件编号CF26构件信息如下：D×t×H=330 mm×6 mm×1 500 mm，升温时间t=60 min，火灾荷载比n=0.2。图3所示为经历火灾全过程后钢管混凝土柱水平荷载-水平位移(P-Δ)滞回骨架曲线试验与本文计算结果对比。可见，计算结果与试验结果总体上吻合良好。

图3 钢管混凝土柱试验与计算结果比较

钢管混凝土组合节点算例取自Song等[11]中编号JCFST2试件，节点信息为：D×t=325 mm×5 mm，H=3.8 m，钢梁H200 mm×120 mm×4.85 mm× 7.63 mm，钢筋混凝土板bslab×tslab=1 000 mm×100 mm，柱防火保护层厚度ac=7 mm，钢梁防火保护层厚度ab=15 mm，升温时间30 min。图4(a)为节点柱顶轴向变形(Δ)-升温时间(t)关系曲线，可见高温作用使得钢材和混凝土材性有着不同程度的劣化，升温初始阶段柱顶轴向压缩变化较快，最终柱端变形趋于平缓，火灾后采用梁端加载破坏方式，故柱轴向压缩变形在后期较小，两者总体吻合良好。图4(b)为梁端竖向变形(Δ)-升温时间(t)关系曲线，经历降温段到火灾后梁端变形急剧加大。计算结果与试验数据吻合良好。

图4 钢管混凝土组合节点变形(Δ)-升温时间(t)关系比较

框架算例选取Han等[13]钢管混凝土柱-钢筋混凝土梁框架耐火试验中编号CFRC-2试件进行框架模型验证。主要参数信息为：钢管混凝土柱截面D×t=140 mm×3.85 mm；钢筋混凝梁尺寸为h×b= 180 mm×100 mm(2Φ16, 2Φ12)；框架柱高1.45 m，跨度2.4 m，柱保护层厚度ac=7 mm。由图5可见，钢管混凝土柱端竖向变形和钢筋混凝土梁跨中挠度变形总体上与试验数据吻合较好，说明该框架建模方法合理。

2.2 力学性能分析

采用上述建模方法建立了考虑火灾全过程作用的钢管混凝土平面框架力学模型，基本信息如下：钢管混凝土柱D(B)×t×H=400 mm×9.3 mm×3 300 mm，钢梁截面为H320 mm×160 mm×7 mm×7 mm，外加强环板宽80 mm，RC楼板bslab×tslab×Lslab=1 000 mm×80 mm×6 000 mm，板内纵向钢筋和分布钢筋均为φ8@200；栓钉为φ16@200，沿梁翼缘轴线方向单排布置，柱含钢率α=0.1，Q345钢。图6(a)所示为平面框架在经历火灾全过程后与常温阶段水平荷载(P)与水平位移(Δ)关系曲线。可见，由于高温作用使得框架水平极限承载力相对于常温框架有所降低。图6(b)为框架柱顶轴向位移(Δ)与升温时间(t)关系曲线，在升温阶段钢材和混凝土材性均有着不同程度的劣化，轴向压缩量较大；进入降温段后，由于钢材性能有一定程度的恢复，使其轴向压缩量减少并最终保持平缓变化趋势。

2.3 水平荷载(P)-变形(Δ)关系分析

以圆截面钢管混凝土柱-组合梁平面框架为例，进行平面框架受火后水平荷载(P)-水平位移(Δ)关系曲线分析。如图6(a)所示，在曲线上选取3个特征点，A为外钢管进入屈服对应点，B为框架水平极限承载力最大值对应点，C为框架极限二倍位移对应点(2Δmax)。通过分析曲线中特征点应力状态，了解其在经历火灾全过程作用的工作机理。图8所示为平面框架特征位置C1、C2、C3分别在A、B、C点的核心混凝土应力分布(取左柱为研究对象)。具体截面位置如图7所示。

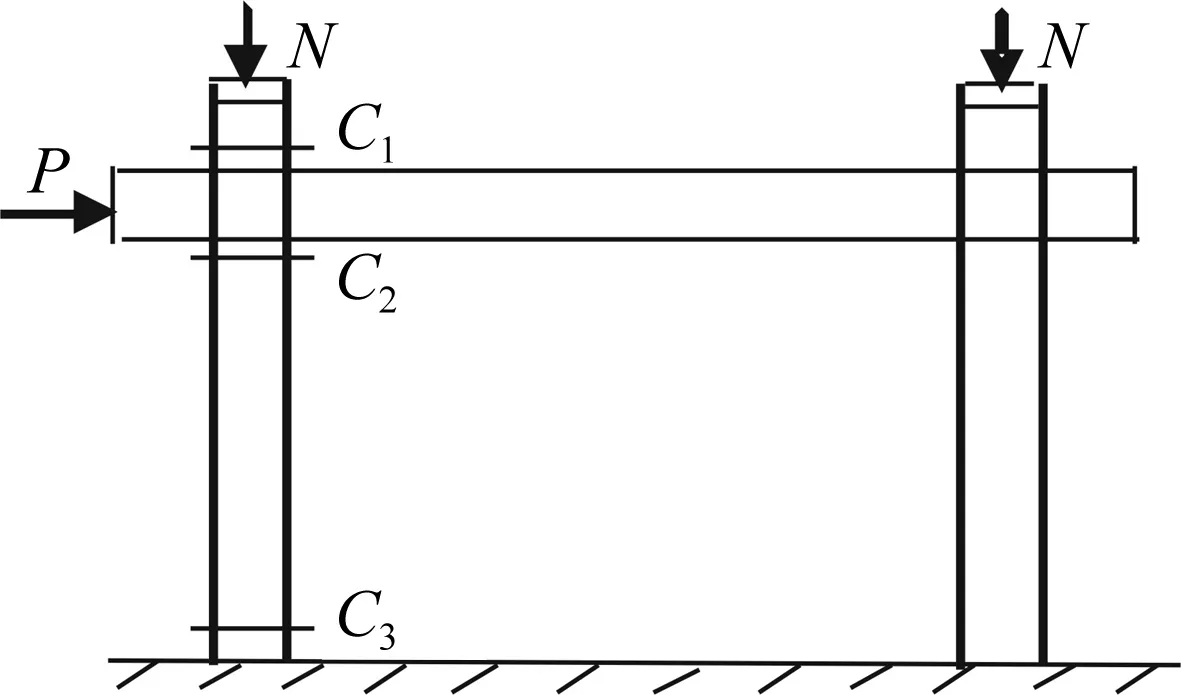
图7 平面框架特征截面位置示意图

由图8可见，对于位置点C1，在特征点A、B、C处核心混凝土处于全截面受压状态，应力分布较均匀。位置C2初期在轴向压力作用下截面处于受压状态，到达A点后由于水平荷载的增大使得柱右半截面压应力区域减小，有向拉应力过渡的趋势；在B点和C点出现了明显的拉应力区，并且随着水平荷载的增大，受拉区面积增大，中和轴向截面中间部位移动。C3位于组合框架柱脚位置，在水平荷载作用下出现明显的受拉区和受压区，且随着水平荷载的增大，受拉区面积也相应增大，中和轴逐渐向截面中间移动。

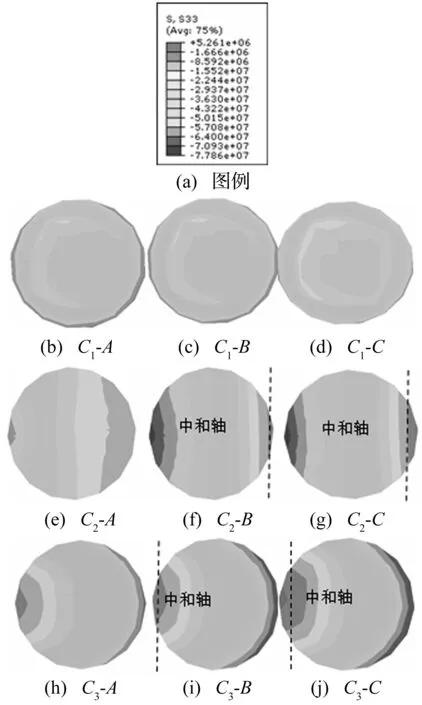
图8 不同截面不同时刻核心混凝土纵向应力分布

图9所示为钢管在特征点A、B、C时刻的纵向应力沿着长度方向分布示意图。可见，在钢管与钢梁相互作用位置以及柱脚位置应力值最大，在反弯点区域应力相对较小，从A点到C点，随着水平荷载的增大，应力和变形增大，受拉区应力面积增大。

图10所示为框架左柱节点核心区在曲线A、B、C相应时刻的应力分布图。可见，随着水平荷载的增大，钢梁和钢管应力相应增大，变形也随之增大；但到达C点后，节点核心区应力有所减小，这是由于水平荷载越大，组合框架右柱部分将分担更多的应力。

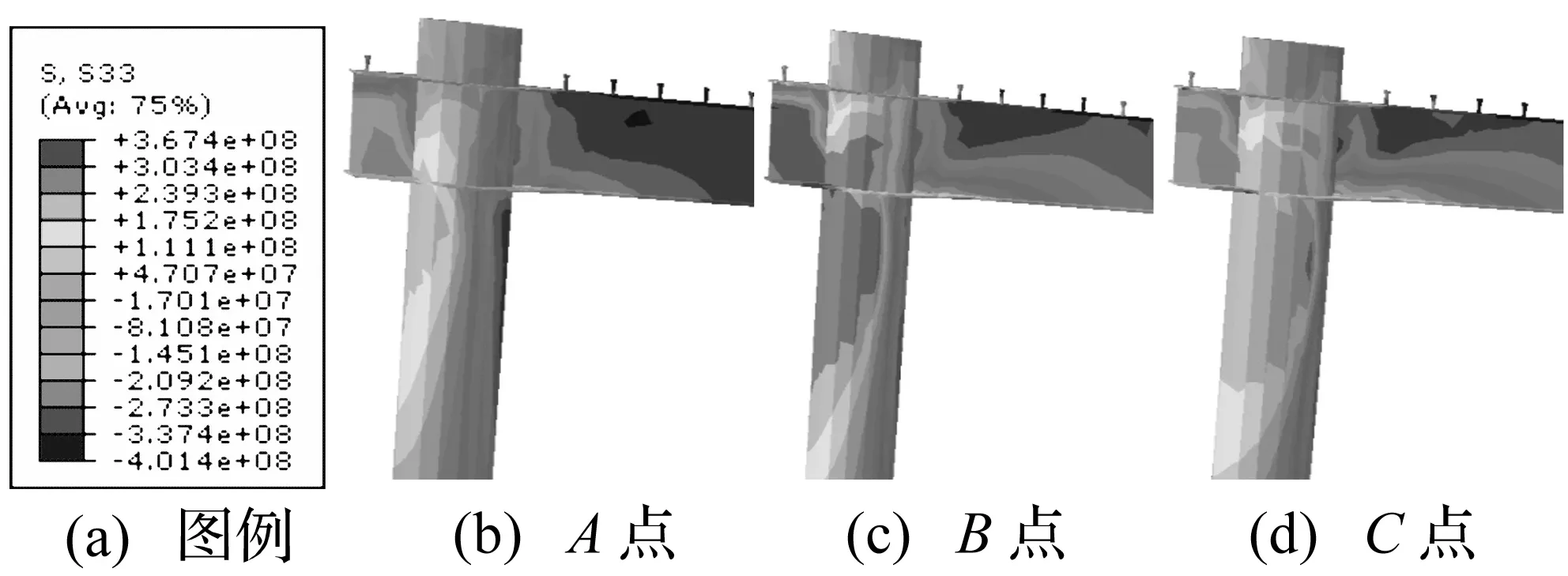
图10 节点核心区应力分布图

3 参数分析

为了解该类结构在经历火灾全过程后的受力性能，对可能影响因素进行参数分析，依据工程常用参数范围进行选取，即火灾荷载比n=0.2～0.8；升温时间比t0=0.2～0.6；框架柱防火保护层厚度a=0～15 mm；钢梁防火保护层厚度按照《建筑设计防火规范》GB50016-2006[18]选取，使梁耐火极限满足2 h，考虑算例中混凝土楼板的吸热作用，取20 mm；框架柱长细比λ=33～80。

3.1 柱火灾荷载比n

柱火灾荷载比定义为n=NF/Nu，其中NF为受火阶段柱顶作用荷载，Nu为常温下钢管混凝土框架柱极限承载力。图11所示为柱火灾荷载比n对钢管混凝土平面框架水平荷载P-水平位移Δ关系曲线影响规律。可见，柱火灾荷载比对P-Δ曲线的形状影响较为显著，随着n的增大，框架水平极限承载力和初始刚度均有所降低；当其达到一定数值时，曲线出现下降段，且下降段的幅度随着n的增大而增大，位移延性越来越小。由图11可见，柱火灾荷载比n对圆截面框架P-Δ曲线形状影响较方截面平面框架明显，主要是由于当n较小时，圆截面钢管对核心混凝土具有更好的约束作用，使得其承载力较高，故P-Δ曲线没有出现下降段。

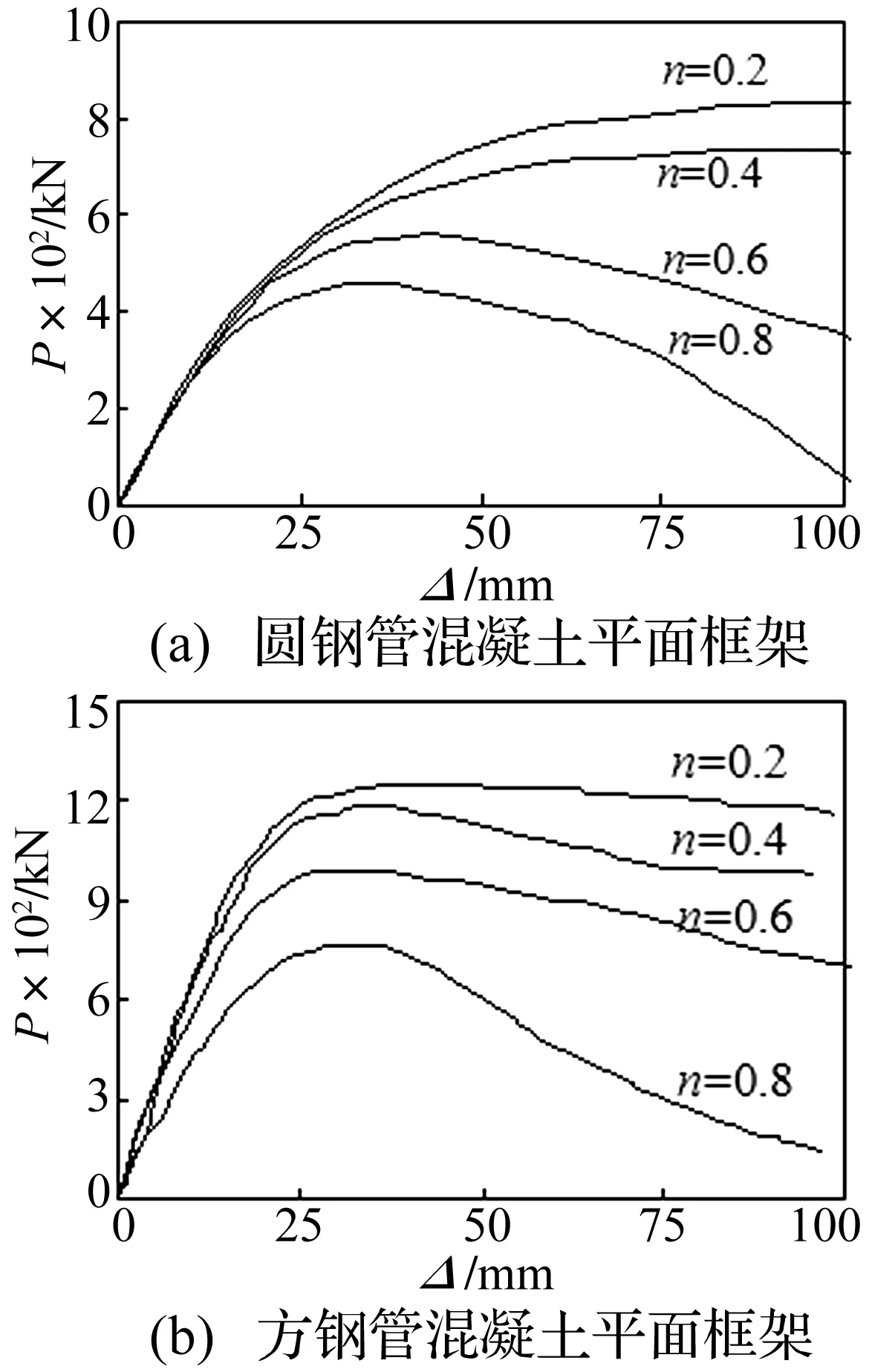
图11 火灾荷载比对P-Δ曲线的影响

3.2 升温时间比t0

图12给出了升温时间比t0对平面框架P-Δ曲线影响规律，其中升温时间比t0定义为：

(4)

式中：th为升降温临界时间；tR为组合框架耐火极限，目前钢管混凝土框架耐火极限的计算公式规范中未给出，

所以本文在计算框架柱耐火极限时参考韩林海[1]中关于钢管混凝土柱耐火极限的计算公式。

由图12可见，随着t0增大框架水平极限承载力降低，且初始刚度也略有所下降。升温时间比t0对圆截面钢管混凝土柱-组合梁平面框架P-Δ关系曲线影响较小，对方截面柱平面框架影响较大。

3.3 柱防火保护层厚度a

图13给出了柱防火保护层厚度a对框架P-Δ曲线影响规律。可以看出a对框架P-Δ骨架曲线的影响较显著，在受火时间t相同的情况下，裸钢管所对应框架的水平极限承载力相对较低，当柱保护层厚度为15 mm时，框架的水平极限承载力基本接近于常温，这与李国强等[19]中所提到的结论是相符合。此外，随着a的增大，圆截面柱平面框架后期刚度和延性有所提高，这主要是由于随着钢管混凝土柱防火保护层厚度的增加，框架的整体温度越低，对钢材和混凝土材性的影响越小，但柱保护层厚度对方柱框架的延性影响并不明显。

3.4 柱长细比λ

图14为柱长细比对钢管混凝土柱-组合梁平面框架的P-Δ曲线影响规律。本文长细比计算中保持框架柱直径D不变，改变其有效高度L0进行计算。由图14可见，柱长细比对P-Δ骨架曲线的数值和形状影响均较显著。随着λ的增大，框架初始刚度和水平极限承载力均有所减小，当长细比分别为60和80时，此时框架初始刚度和水平承载力都很低，且曲线没有出现下降段。柱长细比对圆截面和方截面平面框架影响规律基本一致。

图12 升温时间比对组合框架P-Δ曲线的影响

4 结 论

在本文研究的参数范围内，可初步得到以下结论：

(1) 通过合理选取材料本构模型和边界条件的基础上，建立了考虑火灾全过程作用的钢管混凝土柱-组合梁平面框架有限元模型。结果表明高温作用使得受火后框架整体水平极限承载力和初始刚度均有不同程度降低。

(2) 参数分析结果表明，火灾荷载比和柱长细比对框架P-Δ曲线数值和形状影响较大。当火灾荷载比n较大时，曲线出现明显下降段，后期延性较差。因此，建议该类结构进行参数设计时，柱火灾荷载比宜取0.2～0.6；柱长细比宜取20～40范围内，而且钢管混凝土柱与钢梁均要设防火保护层。

(3) 为进一步系统研究该类结构受火全过程性能，进行相应的试验研究很有必要。

[1]韩林海. 钢管混凝土结构-理论与实践(第2版)[M]. 北京：科学出版社, 2007.

[2]Schaumann P, Kodur V, Bahr O. Fire behaviour of hollow structural section steel columns filled with high strength concrete[J]. Journal of Constructional Steel Research, 2009, 65(8-9): 1794-1802.

[3]任晓虎，霍静思，陈柏生. 火灾下钢管混凝土梁落锤冲击试验研究[J]. 振动与冲击, 2012, 31(20): 110-115.

REN Xiao-hu, HUO Jing-si, CHEN Bai-sheng. Anti-impact behavior of concrete filled steel tubular beam in fire[J]. Journal of Vibration and Shock, 2012, 31(20): 110-115.

[4]Yang H, Han L H, Wang Y C. Effects of heating and loading histories on post-fire cooling behaviour of concrete-filled steel tubular columns[J]. Journal of Constructional Steel Research, 2008, 64(5): 556-570.

[5]Song T Y, Han L H, Yu H X. Concrete filled steel tube stub columns under combined temperature and loading[J]. Journal of Constructional Steel Research, 2010, 66(3): 369-384.

[6]Huo J S, Zeng X, Xiao Y. Cyclic behaviours of concrete-filled steel tubular columns with pre-load after exposure to fire[J]. Journal of Constructional Steel Research, 2011, 67(4): 727-739.

[7]Tao Z, Han L H, Uy B, et al. Post-fire bond between tube and concrete in concrete-filled steel tubular columns[J]. Journal of Constructional Steel Research, 2011, 67(3): 484-496.

[8]霍静思，任晓虎，肖岩. 标准火灾作用下钢管混凝土短柱落锤动态冲击试验研究[J]. 土木工程学报，2012，45(4)：9-20.

HUO Jing-si, REN Xiao-hu, Xiao Yan. Impact behavior of concrete-filled steel tubular stub columns under ISO-834 standard fire[J]. China Civil Engineering Journal, 2012, 45(4): 9-20.

[9]Wang Y C, Davies J M. An experimental study of the fire performance of non-sway loaded concrete-filled steel tubular column assemblies with extended end plate connections[J]. Journal of Constructional Steel Research, 2003, 59(7): 819- 838.

[10]Ding J, Wang Y C. Experimental study of structural fire behaviour of steel beam to concrete filled tubular column assemblies with different types of joints[J]. Engineering Structures, 2007, 29(12): 3485-3502.

[11]Song T Y, Han L H, Yu H X. Concrete filled steel tube stub columns under combined temperature and loading[J]. Journal of Constructional Steel Research, 2010, 66(3): 369-384.

[12]Tan Q H, Han L H, Yu H X. Fire performance of concrete filled steel tubular (CFST) column to RC beam joints[J]. Fire Safety Journal, 2012, 51：68-84.

[13]Han L H, Wang W H, Yu H X. Experimental behaviour of reinforced concrete (RC) beam to concrete-filled steel tubular (CFST) column frames subjected to ISO-834 standard fire[J]. Engineering Structures, 2010, 32(10): 3130-3144.

[14]Han L H, Wang W H, Yu H X. Analytical behaviour of RC beam to CFST column frames subjected to fire[J]. Engineering Structures, 2012, 36: 394-410.

[15]王景玄，张鹏鹏，王文达. 考虑火灾全过程的钢管混凝土组合框架力学性能初步研究[J]. 防灾减灾工程学报，2012, 32(1): 84-88.

WANG Jing-xuan, ZHANG Peng-peng, WANG Wen-da. Preliminary research on mechanical behavior of composite frame with CFST columns after exposure to overall stage of fire[J]. Journal of Disaster Prevention and Mitigation Engineering, 2012, 32(1): 84-88.

[16]吴波. 火灾后钢筋混凝土结构的力学性能[M]. 北京：科学出版社, 2003.

[17]王景玄. 考虑火灾全过程的钢管混凝土组合框架力学性能研究[D]. 兰州：兰州理工大学, 2011.

[18]GB50016-2006. 建筑设计防火规范[S]. 北京：中国计划出版社，2006.

[19]李国强，韩林海，楼国彪,等. 钢结构及钢-混凝土组合结构抗火设计[M]. 北京：中国建筑工业出版社，2006.