齿轮减速器振动噪声预估公式定制方法研究
周建星, 孙文磊, 万晓静
(1.新疆大学 机械工程学院,乌鲁木齐,830047; 2.新疆大学 机械工程博士后流动站,乌鲁木齐,830047)
随着现代工业化程度的不断提高,振动噪声问题也越来越受到重视。工业设施的振动噪声不仅会引起噪声污染,还影响着设备的稳定性及操作舒适性。在汽车领域,NVH已成为汽车业各大制造企业重点关注的问题之一;对于武器载体(如舰船等)振动噪声将直接影响到其隐蔽性及战斗力。
齿轮传动具有效率高,结构紧凑,工作可靠,寿命长等特点,广泛应用于各工业领域中。由于齿轮的结构特性,在其啮合过程中不可避免地存在着齿轮啮合刚度的波动及误差作用,使传动系统发生振动,并通过轴承传递于箱体,不仅影响系统的整体的动态性能,还产生噪声污染。减速器振动噪声研究经历了从定性判断到定量分析的过程,上世纪60年代起,为了简化计算齿轮减速器的振动噪声,Nakamura、Niemann、Kato及Masuda等先后开展了噪声预估公式的研究,他们通过大量的试验测试,总结了减速器辐射噪声的变化规律,提出了一些简化计算方法[1-4],并得到了一定的推广和应用,但其计算准确性上仍存在不足;90年代以来,有限元法、边界元法和无网格等工程计算方法逐渐完善,为噪声预测提供了有效支持[5-7]。在对齿轮减速器振动噪声方面的研究中,以FEM/BEM方法使用最为广泛。文献[8-10]采用FEM/BEM方法对减速器振动噪声进行预测,并通过实验得到了较好的验证。但是减速器振动噪声的数值预估不仅需要较为细致的减速器结构特征以及相关工程经验,求解过程还要消耗大量计算资源,不便于工程设计阶段的使用。
本文以单级齿轮减速器为研究对象,通过FEM/BEM仿真的方法分析了齿轮减速器振动噪声随齿轮精度等级的变化,综合考虑误差与转速和负载的耦合作用关系,拟合得到了考虑齿轮精度等级的减速器噪声预估公式,并通过实验对其准确性进行了验证。
1 减速器噪声预估方法
1.1 经验预估方法
1965年,为了预测齿轮传动系统的振动噪声, Niemann提出了减速器噪声与20logW(W为传动功率)成线性比例关系,并拟合了单级减速器噪声强度的经验公式:
L=50+20logW+∑K
(1)
式中:L为噪声强度(dB);W为传递功率(hp);K为修正值。
1975年,Kato按照Niemann的思路,考虑了传动功率、速度、重合度、传动比、螺旋角、精度等级对减速器辐射噪声的影响,提出了以下的半经验公式:
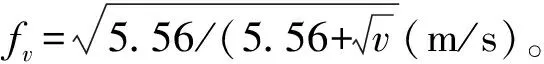
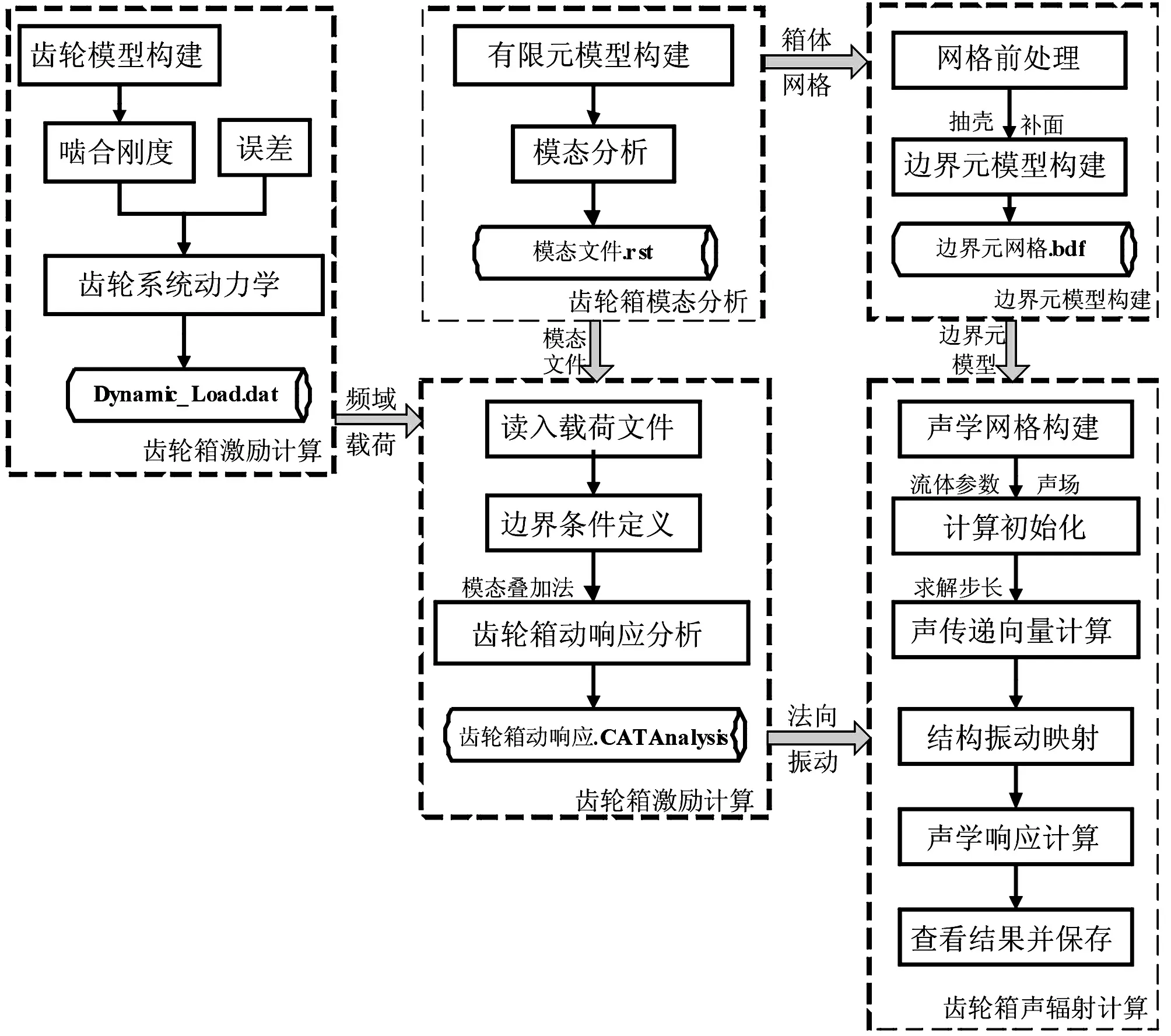
图1 FEM/BEM噪声辐射求解流程
由于Kato公式形式简单,并可以定量地计算出齿轮副的噪声值,在工程设计中得到了一定的应用。但由于公式中无法对齿轮误差形式及齿轮精度对减速器噪声的影响进行合理的体现,故其计算结果仅在少数情况下与实验结果吻合较好。
1.2 FEM/BEM噪声辐射分析方法
在进行声场边界元分析时,一般是以结构表面法向振动加速度作为边界条件,而这些数据主要是通过其他数值方法(如有限元法)计算或者通过试验测得,分析流程如图1所示。首先采用合理的方式对齿轮副时变啮合刚度及误差等激励进行等效,并建立齿轮系统动力学模型,以求解作用于齿轮箱上的动载荷;其次,建立齿轮箱有限元模型,求解齿轮箱结构稳态动响应,并得到齿轮箱表面振动信息;然后,建立齿轮箱声学边界元模型;最后,以结构体表面的法向速度作为边界条件对齿轮箱噪声辐射进行分析。
若能合理的对减速器振动激励进行等价,求取轴承动载荷,则FEM/BEM方法可以有效求解减速器噪声辐射。
2 减速器振动噪声数值计算
2.1 分析模型
分析模型参数如表1所示。

表1 分析模型参数
分析模型如图2所示,为单级直齿圆柱齿轮减速器,模型构建时,对结构中存在的较小的倒角及细小特性进行了适当简化。
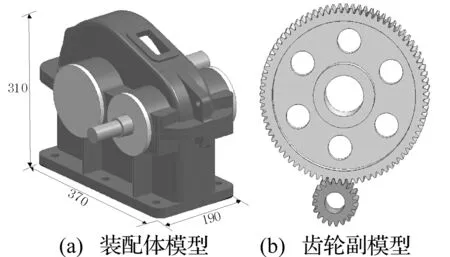
图2 减速器模型
2.2 齿轮箱激励计算
减速器运转过程中,由于齿轮时变啮合刚度及误差激励的作用,使齿轮动态啮合力产生波动,从而引起系统振动。
对齿轮啮合刚度引入有限元接触算法,采用真实齿轮模型,计算得到在啮合线方向上由齿轮轮体,轮齿弹性变形及赫兹接触变形组成的总变形μ。而在该位置的啮合刚度为:
K=T/Rbu
(3)
其中:Rb为齿轮基圆半径;T为负载扭矩。
将一个啮合周期划分为若干等分,分别求取各啮合位置上的刚度。对于其他位置则采用样条插值得到,齿轮时变啮合刚度曲线如图3所示,基本成矩形波形式。
对于误差激励,可以采用简谐函数对其进行模拟,并假设在一个啮合周期中,误差为正弦分布如图3所示,将轮齿误差表示为:
e(t)=ersin(ωt/Tm+φ)
(4)
式中:er为误差幅值,Tm为齿轮啮合周期,ω为主动轮转速,φ为相位角。
2.3 传动系统模型构建
传动系统动力学模型如图3所示,其中p为主动轮,g为从动轮。由于传动轴两轴承间跨度较短,弯曲刚度较大,故不考虑其弯曲变形,因此可将轴承支撑刚度和阻尼用等效值kyp,kyg和cyp,cyg来表示。系统共包含4个自由度,分别为:
yp为主动轮p平移位移;θp为主动轮p转动位移;
yg为从动轮g平移位移;θg为从动轮g转动位移;
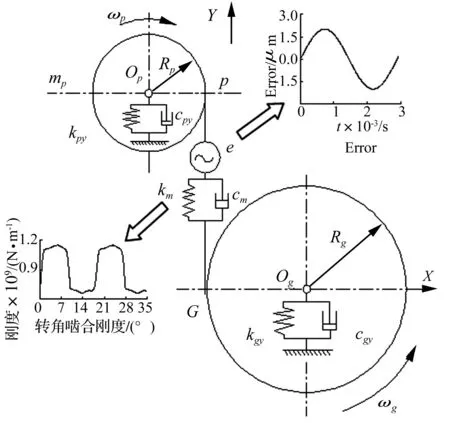
图3 齿轮副动力学模型
轮副的啮合力和啮合阻尼力,可表示为:

式中,km为齿轮啮合刚度,cm为齿轮啮合阻尼,e为啮合误差,Rp、Rg分别为主从动轮基圆半径。
因此齿轮副动态啮合力Fpg为:
Fpg=Fk+Fc
(5)
依据各齿轮受力平衡关系有:
(6)
式中:mp为主动轮质量,mg为从动轮质量,Tp为输入扭矩,Tg为输出扭矩。
方程的矩阵形式为:
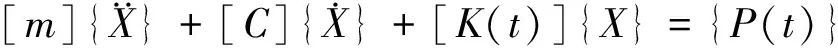
(7)
式中:M、C、K为质量阵、阻尼阵及刚度阵;X为位移向量;P为广义力向量
2.4 减速器振动噪声计算
齿轮箱动响应分析模型如图4所示。采用4面体单元进行网格划分,模型共划分节点38 634个,单元146 238个,箱体材料为铸钢,定义弹性模量E=207 GPa,泊松比υ=0.3,密度ρ=7 800 kg/m3。
作用于输出轴和输入轴的动载荷通过轴承传递于箱体,在主从动轮轴承支承位置建立中心节点,与轴承壁面节点建立耦合关系,将动载荷施加于中心节点。
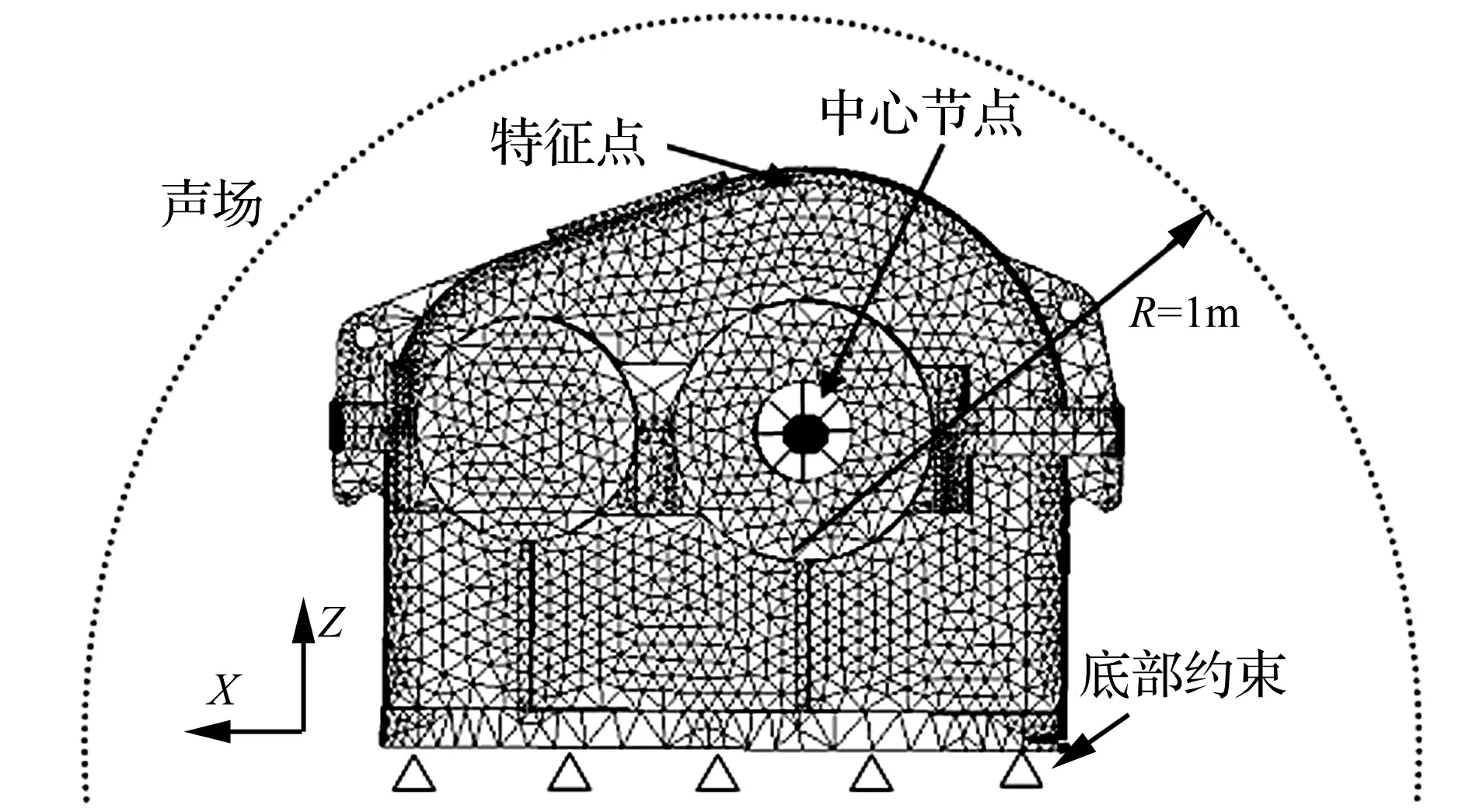
图4 箱体有限元模型
采用Lanczos法对齿轮箱进行模态计算,齿轮箱固有频率如表2所示。

表2 减速器固有频率(Hz)
采用自主研发的一套结构动响应计算流程对齿轮箱动响应进行求解(求解流程详见[11]),得到了齿轮箱结构动响应,以齿轮箱外表面法向振动加速度为边界,采用BEM方法求解齿轮箱噪声辐射。为保证数据输入的正确性,边界元网格与有限元网格采用相同的划分方式,以保证两种模型节点间数据传递的稳定性。
在不考虑误差时,齿轮箱噪声谱如图5所示,由于齿轮箱以扭转振动为主,顶部法向振动分量不大,故顶部场点噪声明显小于两侧;轴承两侧场点呈对称分布,其声压级分布曲线基本一致,并均在齿轮啮合频率的2倍频,4倍频及5倍频位置处产生了峰值,最大峰值出现在二倍频及五倍频位置,为50 dB。

图5 不同位置的箱体噪声谱
由式(8)可计算各场点等效声压级:
(8)
其中:P(t)为时刻t的声压;P0为参考声压;T为求解周期。
采用Kato公式计算可以得到齿轮箱辐射噪声为46.88 dB,通过FEM/BEM方法计算得到齿轮箱各场点噪声分布在41 dB~50 dB之间,故可认为在不考虑误差时,两种方法计算结果具有一致性。
3 计算模型匹配性分析
通过上述分析,可认为算例中减速器在其额定工况下辐射噪声与Kato公式计算结果基本一致,但在修正前还需对分析模型与Kato计算模型的匹配性进行分析,本文主要从减速器噪声辐射随转速及负载的变化两个方面来说明其变化规律的一致性。
3.1 转速对噪声辐射的影响
本文计算了减速器常规工作转速(即500~3 000 r/min)的噪声辐射,并采用瀑布图的方式进行表述,如图6所示,其中fb1为齿轮箱1阶固有频率,fm为齿轮副啮合频率。颜色较深的区域代表噪声辐射较大的位置,可以看到在低速时齿轮箱噪声谱各频率成分均不大,随着转速的增加,噪声辐射逐渐强烈。
各转速在齿轮啮合频率及其倍频位置,均产生了放射状深色区域,但并不明显。在与齿轮箱固有频率较为接近的670 Hz附近,1 300 Hz~1 700 Hz位置以及3 000 Hz~4 000 Hz位置均产生了深色区域,其中由于箱体第二、三、四阶固有频率对激励较为敏感且振动能量较大,故各转速下在该频带产生了强烈的共振区;同时,齿轮箱结构第一阶固有频率及在3 000 Hz~4 000 Hz位置的振型在轴承激励作用下虽然振动能量不大,但其相对法向振动也较强,故在该频带噪声辐射也较为强烈。
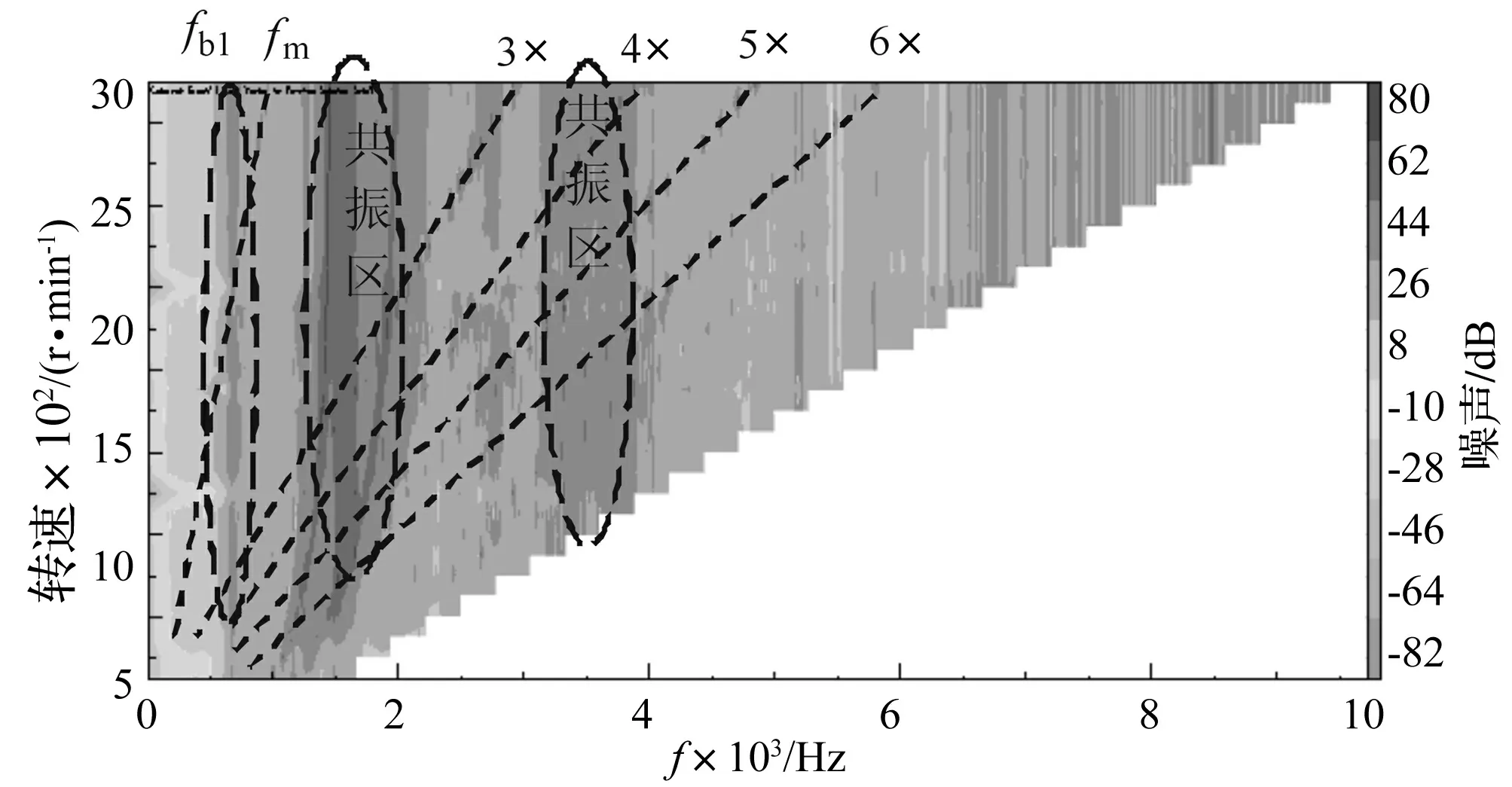
图6 齿轮箱噪声辐射瀑布图
分别计算各转速下齿轮箱辐射噪声有效声压级,同时将转速转换为齿轮线速度,即得到有效声压与线速度的关系,如图7所示,其中曲线a为数值计算结果,b为采用Kato公式计算结果。

图7 箱体辐射噪声随齿轮线速度的变化
由于Kato公式中并未体现传动系统及齿轮箱的固有特性,故计算结果随齿轮线速度的变化趋势较为平滑,减速器噪声随齿轮转速的增加逐渐增大。采用FEM/BEM计算不仅考虑了传动系统及减速器的固有特性,还引入齿轮啮合频率及其倍频激励的作用,故噪声曲线伴随有一定的波动。在750 r/min时,由于激励六次谐波成分与传动系统第一阶固有频率较为接近,使传动系统产生了较大的振动,噪声辐射偏离曲线d1=7 dB;在2 100 r/min时,由于齿轮啮合力二次谐波成分(1 398 Hz)与齿轮箱第二阶固有频率较为接近,引起了齿轮箱较大的振动,使噪声辐射偏离曲线d2=5 dB。若去除这两个共振位置,其他位置两曲线相差均未超过3 dB,因此仿真计算结果与Kato计算结果基本吻合。
3.2 负载对减速器振动噪声的影响
对于传动系统,负载不改变各激励频率成分,仅对各频率成分的幅值有一定影响,并成线性变化。在不改变转速的前提下,计算了负载分别为0.5×T,T,及3×T(其中T为工作载荷)减速器噪声辐射,如图8所示,可以看到随着负载的增加,减速器辐射噪声在各个频率均有所增加,并在激励基频及其主要倍频位置附近增加较为明显,各峰值位置均未发生改变。

图8 箱体噪声随负载的变化
由式(8)计算了各位置场点等效声压级分别为43.66 dB,49.53 dB及55.84 dB,可以发现,在转速不变时,辐射噪声与负载的变化符合,Kato公式的函数关系,即:
L(n×T)=20logn+L(T)
(9)
其中:n为负载的比例系数,T为负载,L(T)为负载为T时齿轮箱辐射噪声。
4 振动噪声预测公式拟合
4.1 误差合成方法
在齿轮动力学计算中,通常将误差合成值当量至啮合线上进行计算,而齿形误差和基节偏差均为齿面交线间法向距离的理论值与实际值差的最值,故可直接将两项误差进行合成。
如果已知齿轮的齿形误差ff和基节偏差Fpb值,则可以用代数和来计算齿轮的固有位置误差,通常情况下齿轮误差的合成需转换到节圆上进行度量,此时齿轮固有位置误差为:
(10)
对于一批合格齿轮来说,齿形总误差、基节偏差均在其公差范围内变化,故采用统计方法来计算齿轮短周期误差[12],建立精度等级与误差值的数值关系,如图10所示,将各精度合成误差带入动力学模型中进行计算,计算中取系统转速为1 000 r/min,为避免计算中出现脱啮和齿背冲击等非线性响应,故增大功率至30 kW。
4.2 减速器噪声预估公式拟合
齿轮精度分别为5、6、7级时的噪声谱,如图9所示,与不考虑误差时相比较,考虑误差后其噪声谱在齿轮啮合频率位置出现了明显的峰值,同时在前几阶倍频位置(4倍频)的噪声也明显增大,对高频位置其影响不明显。随着误差的增大,各峰值也逐渐增大。
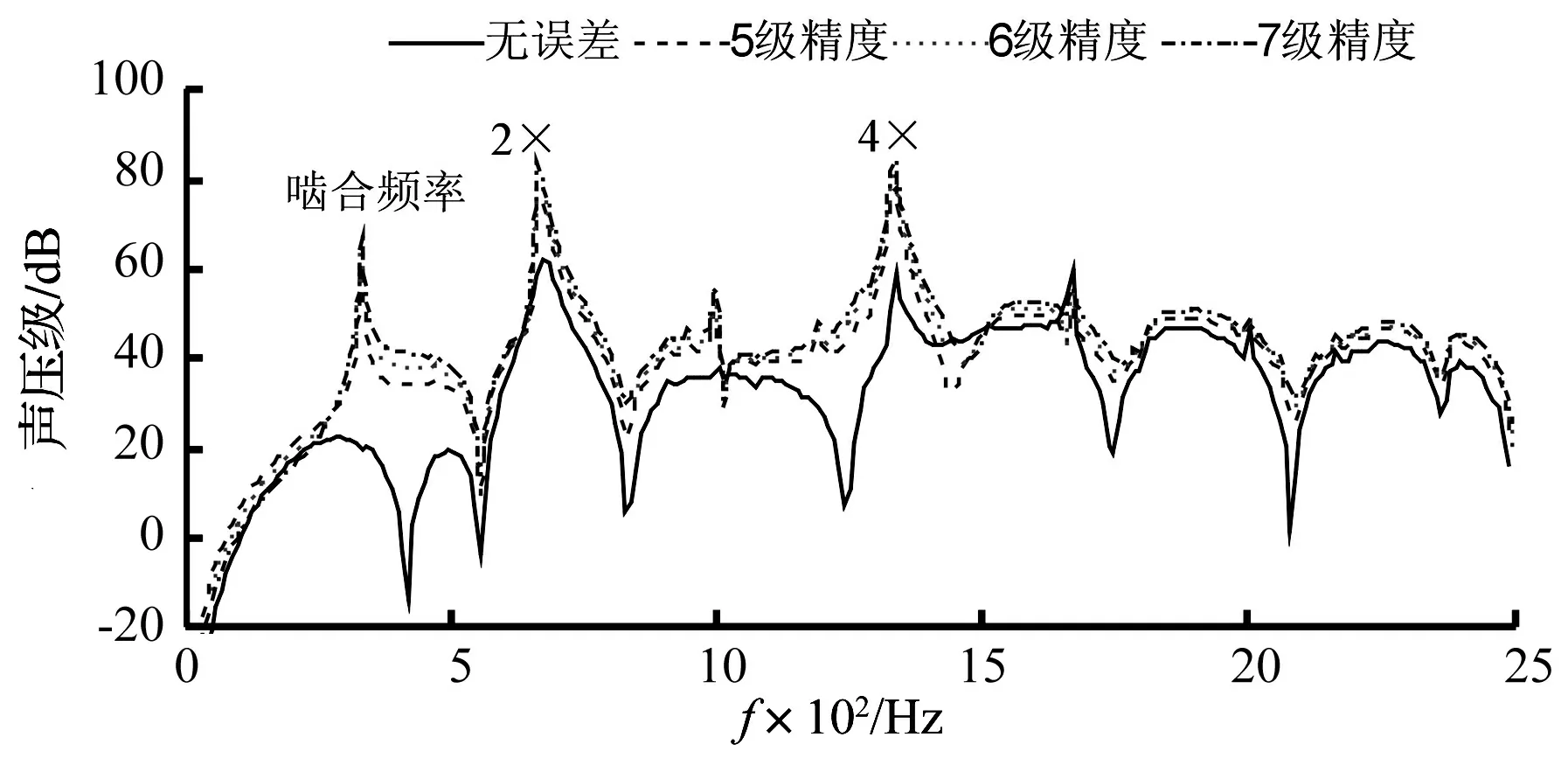
图9 不同齿轮精度下的噪声谱
分别计算各精度等级的齿轮箱有效噪声,得到齿轮箱噪声辐射随精度等级变化曲线,如图10所示。

图10 减速器噪声及合成误差随精度等级的变化
可以看到随精度等级增加,误差的增大,齿轮箱有效噪声呈线性增大,通过拟合可以得到其函数关系为:
Y=A+B·X
(11)
其中:A为无误差时齿轮箱有效噪声58.84 dB,B为有效噪声随精度等级变化的梯度2.85。
结合Kato公式,得到考虑精度等级的齿轮传动装置振动噪声预估公式如式12所示。
(12)
其中:Q为齿轮精度等级。
4.3 减速器噪声预估公式拟合
传动系统转速及负载不仅影响着误差激励在系统动载荷中的频率成分,还影响各频率成分的数值,为进一步分析工况条件对误差激励的影响,定义齿轮精度每变化一级,减速器噪声辐射的变化量为减速器噪声随齿轮精度的变化率,用符号DQ表示,即
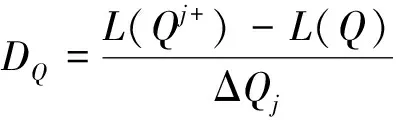
(13)
其中:L(Q)为精度等级为Q时的有效声压级;mQ为最高精度等级。
分别计算了转速为500~3 000 r/min时,减速器辐射噪声随误差的变化率,如图11(a)所示。可以看到其分布均在2.85附近(最大偏差仅为0.15),并且未呈现出规律性。可以认为转速对误差激励在该工况范围内影响不大,在噪声预估公式拟合中可以不必考虑转速对误差项的影响。
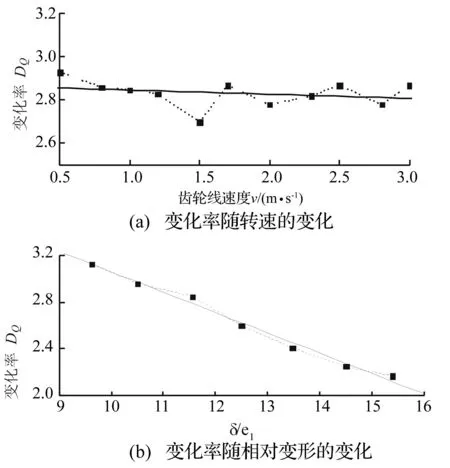
图11 变化率随工况条件的变化
分别计算了负载扭矩为230~380 N·m时齿轮箱辐射噪声,计算中发现当负载增加时齿轮箱辐射噪声随精度的变化率逐步减小,而负载本身对误差激励并不会产生影响,但是负载的增加会使齿轮弹性变形增加,从而使齿轮刚度激励影响增加,误差激励的影响随之减弱,最终使噪声随误差的变化率逐渐减小。
在描述噪声辐射随精度等级的变化率时,引入相对变形量δr(齿轮副静变形量与精度等级为1时的合成误差值的比值),即:
δr=δ0/e1
(14)
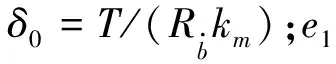
变化率随相对变形量的变化如图11(b)所示,可以看到,随着静变形量的增加,变化率线性减小,通过拟合可以得到变化率随相对变形量的函数关系为:
Y=A+B·X
(15)
其中:A为4.78,B为-0.17。
综合考虑负载及转速对变化率的影响,得到减速器噪声预估计算公式为:

(16)
5 试验验证
减速器噪声测试试验设施由变频驱动电机、输入输出传感器、被测传动装置、加载装置、声学分析仪等组成,布局如图12所示。测试声压时测点距离齿轮箱1 m左右。

图12 试验设施布局
试验中测试两种工况条件下的减速器辐射噪声,工况如表3所示。
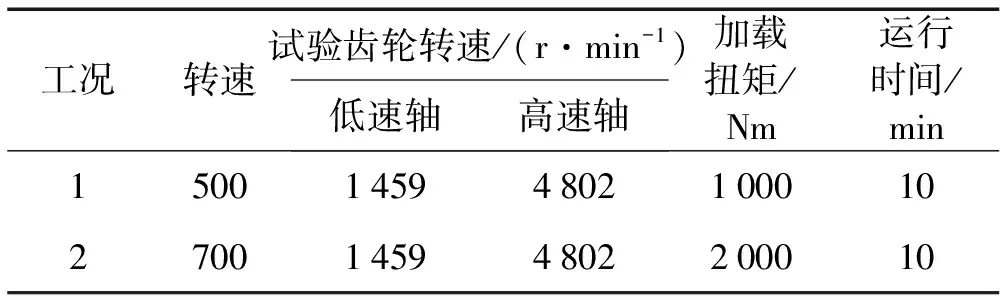
表3 试验工况条件
试验中,测试样机参数如表4所示。

表4 测试样机参数
分别测得两种工况下的噪声频谱,如图13所示,工况1条件下啮合频率噪声声压幅值为0.12 Pa,工况2条件下啮合频率噪声幅值为0.32 Pa。
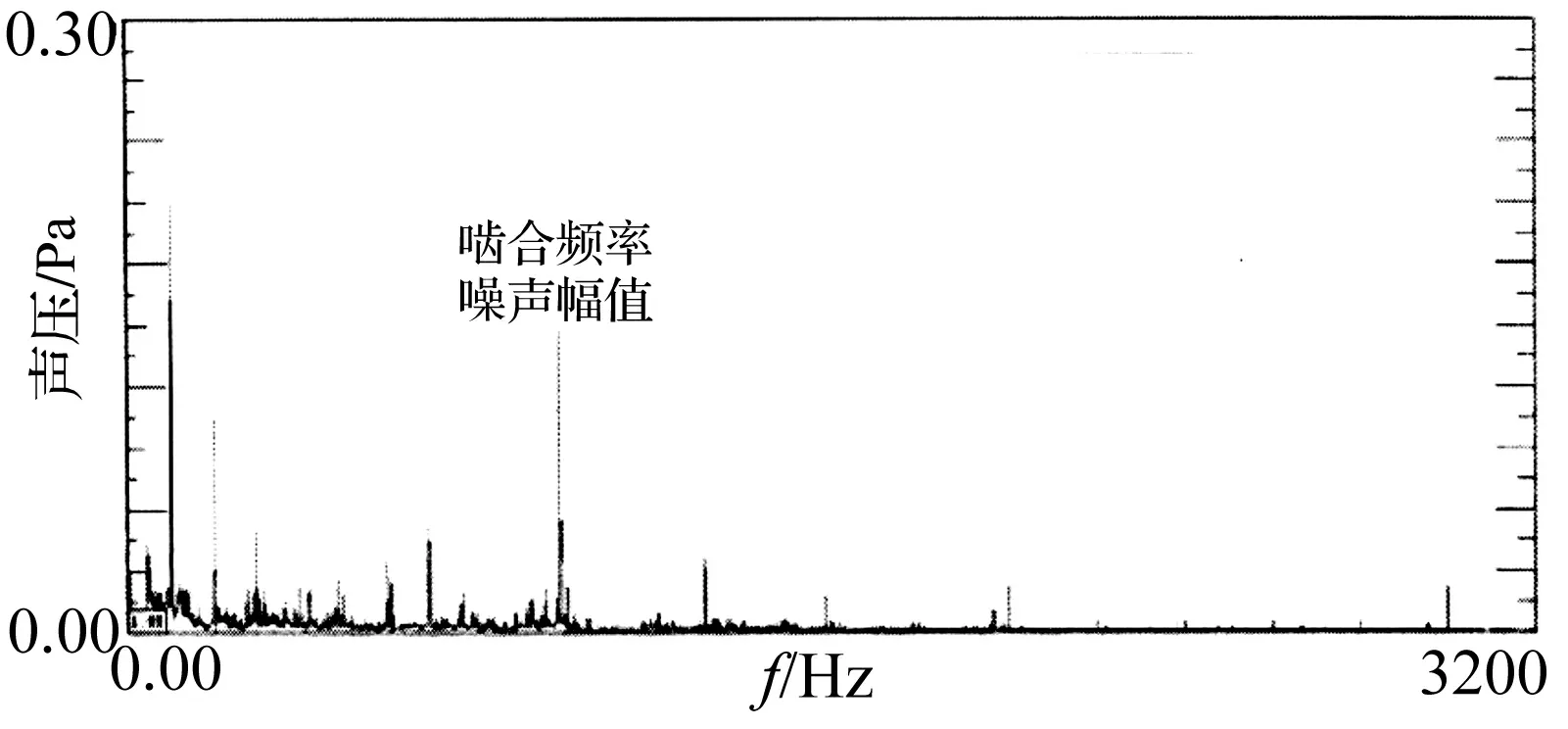
(a) 1 000 N·m,500 r/min工况下测量结果

(b) 2 000 N·m,700 r/min工况下测量结果
通过减速器噪声预估公式16计算的结果与试验测试结果,如表5所示,可以看到在两种工况下,预估计算结果与试验结果均比较吻合。以此证明了预估公式计算的准确性。
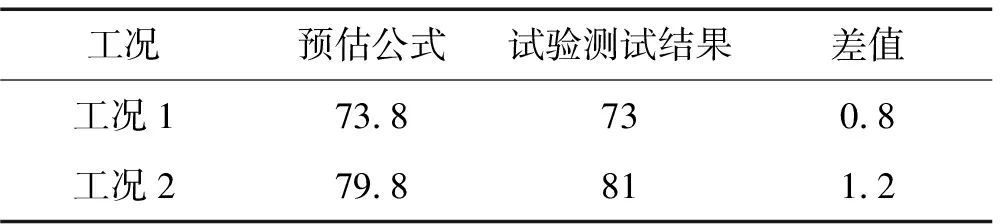
表5 预估与测试结果 (dB)
6 结 论
(1) 仿真计算中可考虑传动系统和减速器的固有特性。若去除共振位置,则通过仿真得到了噪声随转速的变化,与Kato公式所述趋势基本吻合。
(2) 在转速不变的条件下,通过仿真计算发现减速器辐射噪声与负载成20 log函数关系变化,与Kato公式所描述规律一致。
(3) 齿轮箱辐射噪声随精度等级基本呈线性变化,综合考虑误差与转速和负载的耦合作用关系,拟合了减速器噪声预估公式,可实现由减速器基本系统直接预测其辐射噪声的功能。
(4) 开展了减速器振动噪声测试试验,对试验结果与拟合公式计算结果进行了对照,验证了减速器噪声预估公式的准确性。
参 考 文 献
[1]Yuruzume I, Mizutanz H, Tsubuku T. Transmission errors and noise of spur gears laving uneven tooth profile errors[J]. Journal of Mechanical Design, 1979, 101(4): 268-373.
[2]李润方,王建军. 齿轮系统动力学—振动、冲击、噪声[M].北京: 科学出版社, 1997.
[3]Teruo M, Toru A, Kanji H. Prediction method of gear noise considering the influence of the tooth flank finishing method[J]. Journal of Vibration,Acoustics, Stress,and Reliability in Design, 1986,108:95-99.
[4]张策,梁钟. 对于渐开线齿轮噪声计算公式的修正[J]. 天津大学学报, 1983, 3: 85-91.
ZHANG Ce, LIANG Zhong. A modificatin of the noise calculating formula of the involute gear[J]. Journal of Tianjin University. 1983, 3: 85-91.
[5]朱才朝,秦大同,李润方. 车身结构振动与车内噪声声场耦合分析与控制[J].机械工程学报, 2002, 38(8):54-58.
ZHU Cai-chao, QIN Da-tong, LI Run-fang. Study on coupling between body structure dynamic and interior noise[J]. Chinese Journal of Mechanical Engineering,2002, 38(8):54-58.
[6]程昊,高煜,张永斌,等. 振动体声学灵敏度分析的边界元法[J]. 机械工程学报, 2008, 44(7): 45-51.
CHENG Hao, GAO Yu, ZHANG Yong-bin, et al. Boundary element method for acoustic sensitivity analysis of vibrating structures[J]. Chinese Journal of Mechanical Engineering,2008, 44(7):45-51.
[7]Bouillard P, Suleau S. Element-free garlekin solutions for helmholtz problems: formulation and numerical assessment of the pollution effect[J]. Computer Methods in Applied Mechanicals and Engineering, 1998, 162: 317-335.
[8]Kato M, Inoue K, Shibata K, et al. Evaluation of sound power radiated by a gearbox[C]. Proc. Inter Gearing’94, 1994. 69-74.
[9]陆波,朱才朝,宋朝省,等.大功率船用齿轮箱耦合非线性动态特性分析及噪声预估[J].振动与冲击,2009,28(4):76-80.
LU Bo, ZHU Cai-chao, SONG Chao-sheng, et al. Coupled nonlinear dynamic characteristics analysis and noise predestination of a large burden marine gearbox[J]. Journal of Vibration and Shock, 2009, 28(4): 76-80.
[10]王文平,项昌乐,刘辉. 基于FEM/BEM变速器箱体辐射噪声的研究. 噪声与振动控制, 2007,27(5):107-111.
WANG Wenping, XIANG Changle, LIU Hui. Study on the radiation noise of gearbox housing based on FEM/BEM[J]. Noise and Vibration Control, 2007, 27(5): 107-111.
[11]周建星,刘更,马尚君. 内激励作用下齿轮箱动态响应与振动噪声分析[J].振动与冲击,2011,30(6):234-238.
ZHOU Jian-xing, LIU Geng, MA Shang-jun. Vibration and noise analysis of gear transmission system[J]. Journal of Vibration and Shock,2011, 30(6): 234-238.
[12]卜忠红. 人字齿行星齿轮传动系统的动态特性研究[D]. 西安:西北工业大学,2011.

