中型浮动冲击平台结构设计研究
王 军, 姚熊亮, 郭 君
(哈尔滨工程大学 船舶工程学院,哈尔滨 150001)
舰载设备抗冲击能力是舰船的抗爆抗冲击性能的重要组成部分[1],对于小型设备可在冲击机上进行冲击试验,而对大中型舰载设备,由于尺寸和重量较大,无法在冲击机上进行试验考核。目前我国对大中型舰载设备的考核还是一片空白,只在中国船舶科学研究中心和葫芦岛海军基地各有一艘小型浮动冲击平台,可对小于8t的舰载设备进行抗冲击考核。而美国根据MIL-S-901D设备抗冲击考核规范,应用浮动冲击平台,对大中型舰载设备的抗冲击性能形成了标准化的考核试验[2]。
浮动冲击平台的结构形式为矩形平底驳船,两侧及艏艉是抗冲击围壁。设备安装于平台浮动冲击内部,顶部由防水幕布覆盖。美国浮动冲击平台按考核设备重量的范围分为三类:标准浮动冲击平台、中型浮动冲击平台和大型浮动冲击平台。其主要用于水面舰船的大中型舰载设备(如轴系、管系、柴油机、燃气轮机等)的抗冲击考核试验。我国对小型浮动冲击平台在水下爆炸作用下的冲击环境进行过试验研究[3-4],而对中型及大型浮动冲击平台的研究还处在理论计算及数值仿真阶段[5],主要是对美国的标准浮动冲击平台及大型浮动冲击平台进行有限元计算[6]。
舰载设备大部分重量都不超过100 t,美国标准浮动冲击平台只能考核54 t以下的设备,而大型浮动冲击平台考核极限为181 t,对于很多不超过100 t的舰载设备无法应用标准浮动冲击平台,而又没必要使用尺寸较大的大型浮动冲击平台。美国近年来在MIL-S-901D规定的标准和大型浮动冲击平台基础上,又出现中型浮动冲击平台,可对小于113 t的设备进行考核。本文在现有资料基础上,对浮动冲击平台的响应进行分析,设计满足设备考核使用要求的中型浮动冲击平台结构形式,可对我国用于大型舰载设备考核的浮动冲击平台的建设提供参考。
1 中型浮动冲击平台设计基础
结构动力学的三要素是输入(激励)、系统(结构)和输出(响应)。已知激励和系统,问题归结为响应预测,也就是已经知道系统的结构动力学方程和输入的激励载荷,求解结构的动态特性(包括固有频率、振型和阻尼)和动态响应(包括时域响应与频域响应)。同时,工程中经常还会遇到需要解决两类逆问题:已知系统与响应,问题归结为激励识别;已知激励与响应,则问题成为系统识别[7]。
由于美国MIL-S-901D规范并没有给出中型浮动冲击平台的具体结构形式和浮动冲击平台应当输出的冲击环境,只是给定如图1所示的的四个工况[8],按照工况进行试验,若考核试验结束后设备仍能正常运转,则设备抗冲击考核合格。为了进行浮动冲击平台结构设计,输入激励采用MIL-S-901D规定的试验工况,还必须确定输出响应,根据我国设备抗冲击考核现状,主要采用美国标准与德国BV043/85标准,在此输出采用对设备抗冲击较为严格的BV043/85标准。这样浮动冲击平台结构设计就成为上述的系统识别问题,设计思路如图2所示。
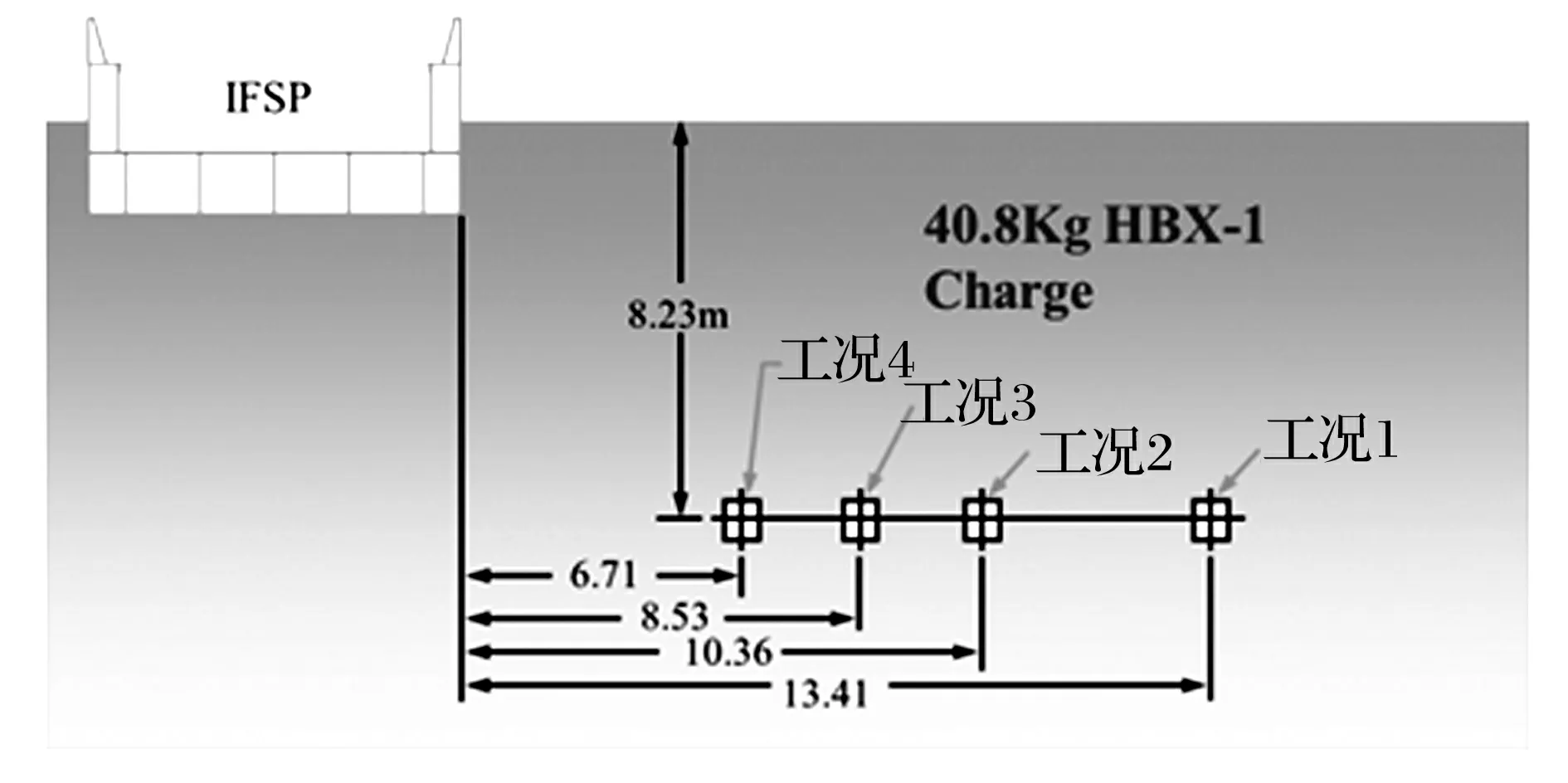
图1 中型浮动冲击平台工况设置
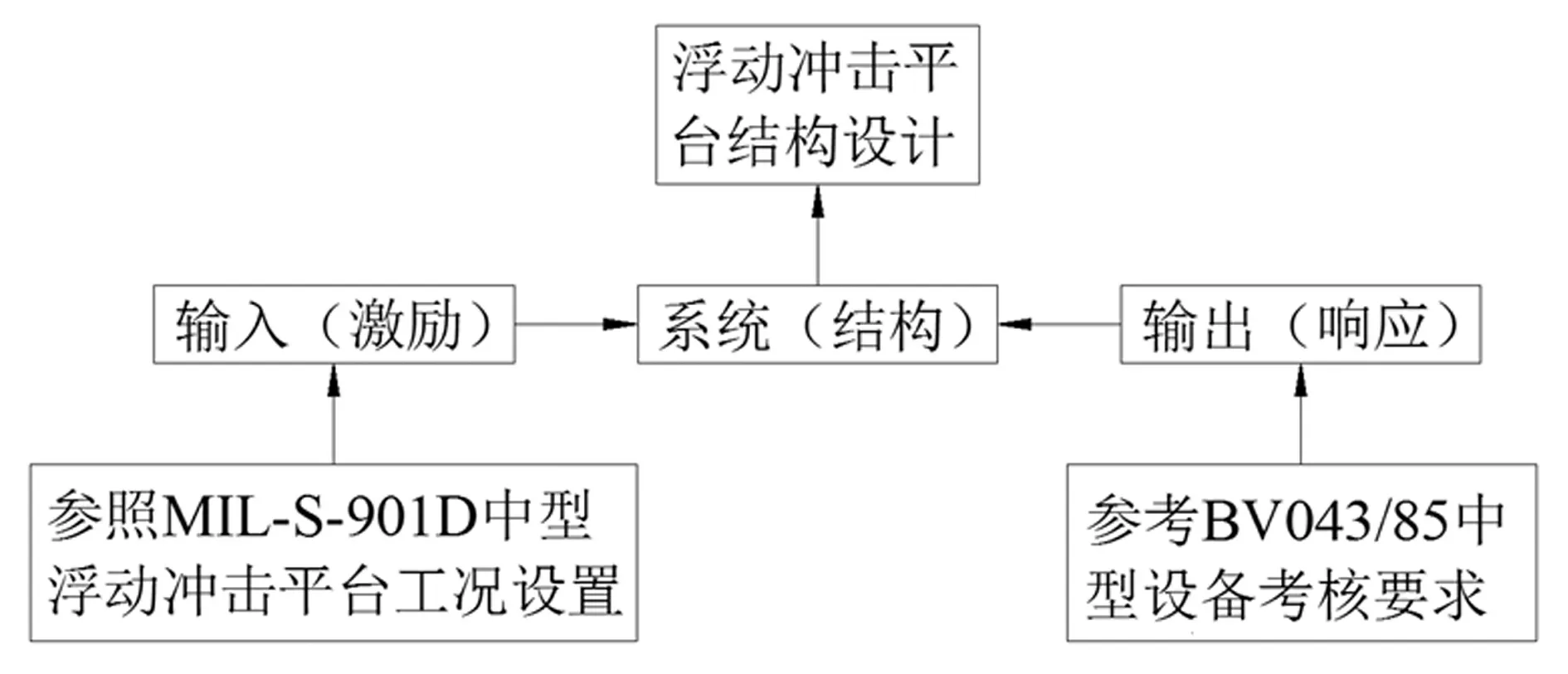
图2 浮动冲击平台结构设计思路
2 浮动冲击平台水下爆炸响应
舰船在水下爆炸的响应主要分为刚体运动和弹塑性变形,刚度大的船体结构刚体运动会比较明显[9]。在对浮动冲击平台的结构设计之前,应先对其在水下爆炸作用下的响应进行计算,分析浮动冲击平台的主要响应为刚体运动还是弹塑性变形,从而对浮动冲击平台的结构刚度等有初步认识。在此以美国中型浮动冲击平台为计算模型,分析水下爆炸时的响应,可为本文浮动冲击平台的结构设计提供指导。
在水下爆炸过程中,浮动冲击平台会受到由冲击波引起的各种不同载荷,如图3所示。首先是冲击波的作用,之后由于自由液面及海底的反射,会形成海底反射波和自由水面反射波,也就是水面截断效应,同时还存在自由面的片空泡及气泡脉动,爆炸产生的水柱和喷水水墩也由爆炸处向四周推进[10]。整个水下爆炸是一个非常复杂的过程[11],现有计算方法很难统筹兼顾。为对浮动冲击平台的响应进行较准确的计算,考虑流体的可压缩性、浮动冲击平台在球面冲击波作用下的响应非线性及浮动冲击平台与流体的流固耦合效应,采用非线性双渐进法进行分析。
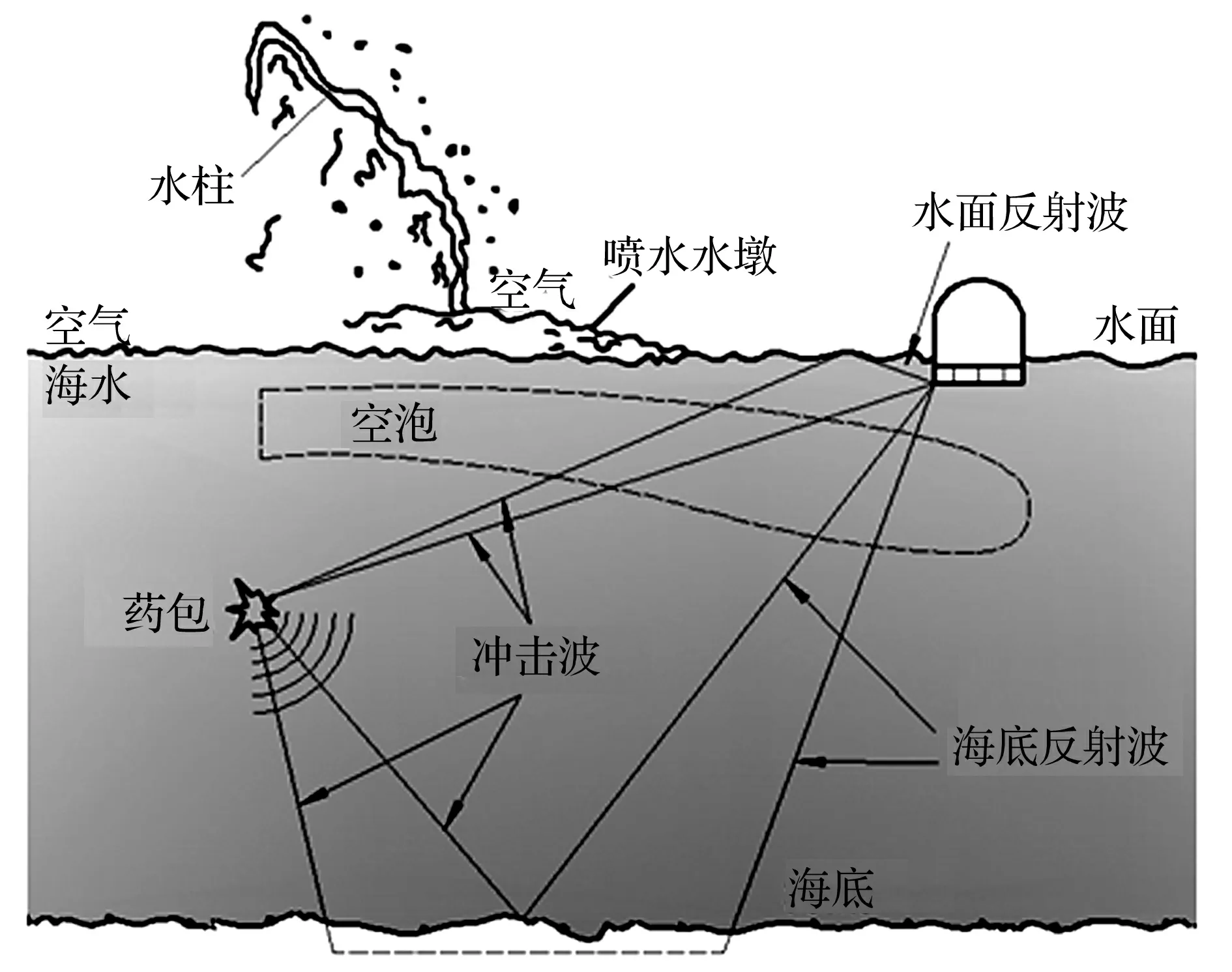
图3 水下爆炸现象概述
考虑可压缩流体的势函数微分方程式
(1)
式中:c为流体的压缩波速度,r为空间矢量坐标,t为时间坐标,势函数φ(r,t)表示为
φ(r,t)=φl(r,t)+φS(r,t)
(2)
其中φl(r,t)为入射波速度势,φS(r,t)为散射波速度势。采用线性假设,压强p与速度势φ有下列关系
(3)
得到二阶双渐进法方程

(4)
式中:ps为流体中的散射压力,Mf为流体质量矩阵,Ωf为流体频率矩阵,Af为流体单元的面积矩阵,uI为入射波速度,u刚和u弹分别为浮动冲击平台的刚体运动速度和单元弹性振动速度。通过伯努利方程得到流体动压力
(5)
其中V为结构运动速度,考虑了结构的航速效应和运动非线性。采用三角形单元对结构进行离散,即可按照文献[12]提供的方法进行求解。
由上述非线性双渐进方法可求得浮动冲击平台刚体平动和转动的动能及增加的势能之和Ek
(6)
根据刚体动能及增加势能之和Ek占冲击波入射能量的比重,可对浮动冲击平台的刚体运动进行分析。下面需对冲击波作用于浮动冲击平台的能量进行求解,冲击波携带的能量为
E=4πR2Ef
(7)
式中Ef为能流密度。冲击波的入射能量为
(8)
其中Se为结构在垂直于冲击波波阵面上的投影面积,可用数值模拟编程的方法进行求解,如图4所示。

图4 投影面积数值模拟图
按照图1所示MIL-S-901D规定的4个工况分别进行计算,得到各工况下的冲击波入射能Es和浮动冲击平台的刚体运动动能Ek如表1所示。
各个工况,浮动冲击平台的刚体运动能量约占冲击波入射能的70%左右,浮动冲击平台响应中刚体运动占主要部分。应用本文方法计算得到的浮动冲击平台刚体运动速度,和美国H.I.-TEST实验室与Kwon等[13]所进行的标准浮动冲击平台试验所得结果比较吻合,验证了本文理论计算方法的正确性。对工况4作用下浮动冲击平台的内底板冲击环境进行分析,如图5所示,黑色虚线表示内底板节点总体响应形成的冲击环境,蓝色实线为节点刚体响应绘出的冲击环境,可以看出浮动冲击平台冲击环境的形成主要来源于平台刚体运动。因此,在浮动冲击平台结构设计时,应保证结构强度要求的条件下,尽量增大浮动冲击平台结构刚度。
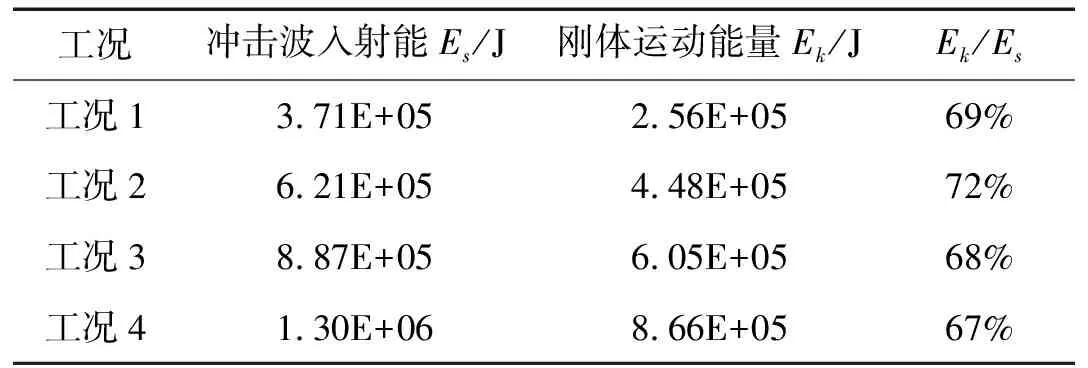
表1 不同工况计算结果

图5 工况4冲击谱对比
3 浮动冲击平台结构设计
根据上述分析,在进行浮动冲击平台结构设计时,只需保证浮动冲击平台具有一定的刚度,即在MIL-S-901D规定的工况下,能有足够的强度抵抗水下爆炸载荷作用下的冲击,同时能够提供BV043/85要求的设备冲击环境即可。根据美国中型浮动冲击平台的主体尺寸,参考标准和大型浮动冲击平台的结构形式,初步设计两种浮动冲击平台结构形式:普通结构形式和箱形梁结构形式。如图6~图7所示,两种结构形式各位置的板厚对应相同,材料都采用舰用945钢,普通结构形式围壁及舷墙通过T型材加强,而箱形梁结构型式的围壁用箱形梁加强。
按图1所示的工况,采用冲击因子最大的工况4进行水下爆炸计算,来确定较好的浮动冲击平台结构形式。通过水下爆炸数值仿真计算得到的节点位移云图如图8~图9所示。经计算后得出普通结构形式的最大变形为70 cm,发生在背爆面轻型舷墙部分,而箱形梁结构形式的最大变形为8 cm,发生在迎爆面轻型舷墙部分,优于普通结构形式。

图6 普通结构形式

图8 普通结构形式节点位移
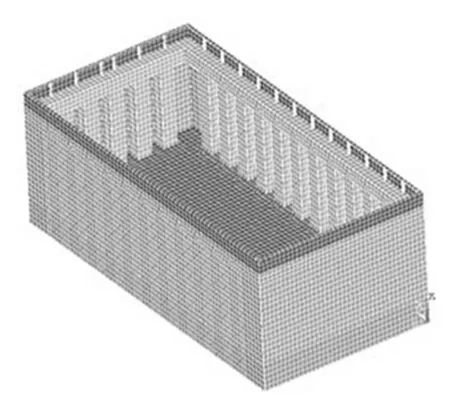
图10 低舷墙箱形梁结构形式
根据浮动冲击平台的最大变形,可以看出箱形梁结构形式强度较好,但轻型舷墙部分最大变形8 cm。平台变形较大不利于重复使用,现对箱形梁结构形式进行优化设计。由于最大变形出现在舷墙顶端部分,因此降低其高度,如图10所示,优化后的低舷墙箱形梁结构形式最大变形出现在迎爆面抗冲击围壁,变形为1.5 cm。此时抗冲击围壁成为薄弱部分,为使结构进一步加强,四周采用夹层结构,外板增加夹层结构后,浮动冲击平台的质量有较大增加,为减轻平台自身的重量,同时为便于设备安装和试验仪器布置,内底板设置若干开孔,形成外板夹层箱形梁结构形式,如图11所示。
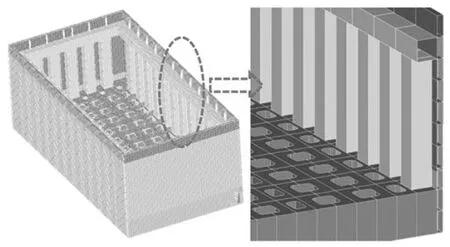
图11 外板夹层箱形梁结构形式
优化后的外板夹层箱形梁结构形式塑性变形区域及范围明显减小,最大变形小于1 cm,发生在迎爆面底部。
因此通过ABAQUS水下爆炸计算分析,低舷墙箱形梁结构形式和外板夹层箱形梁结构形式强度较好,整体变形较小,可满足重复试验要求。但外板夹层箱形梁结构由于增加了夹层结构,自身重量会比低舷墙箱形梁结构形式偏大,因此在中型浮动冲击平台结构设计时,可灵活选择平台的结构形式,达到重量和强度的具体要求。

图12 设备安装于内底板上
浮动冲击平台的强度满足试验要求后,需对内底板上的冲击环境进行分析,确定是否满足BV043/85规范要求。选择某一舰载设备安装于平台内底板上,在此以增压锅炉为例,采用上述分析中强度最好的外板夹层箱形梁结构形式的浮动冲击平台,如图12所示,得到设备基座处的冲击环境如图13所示。
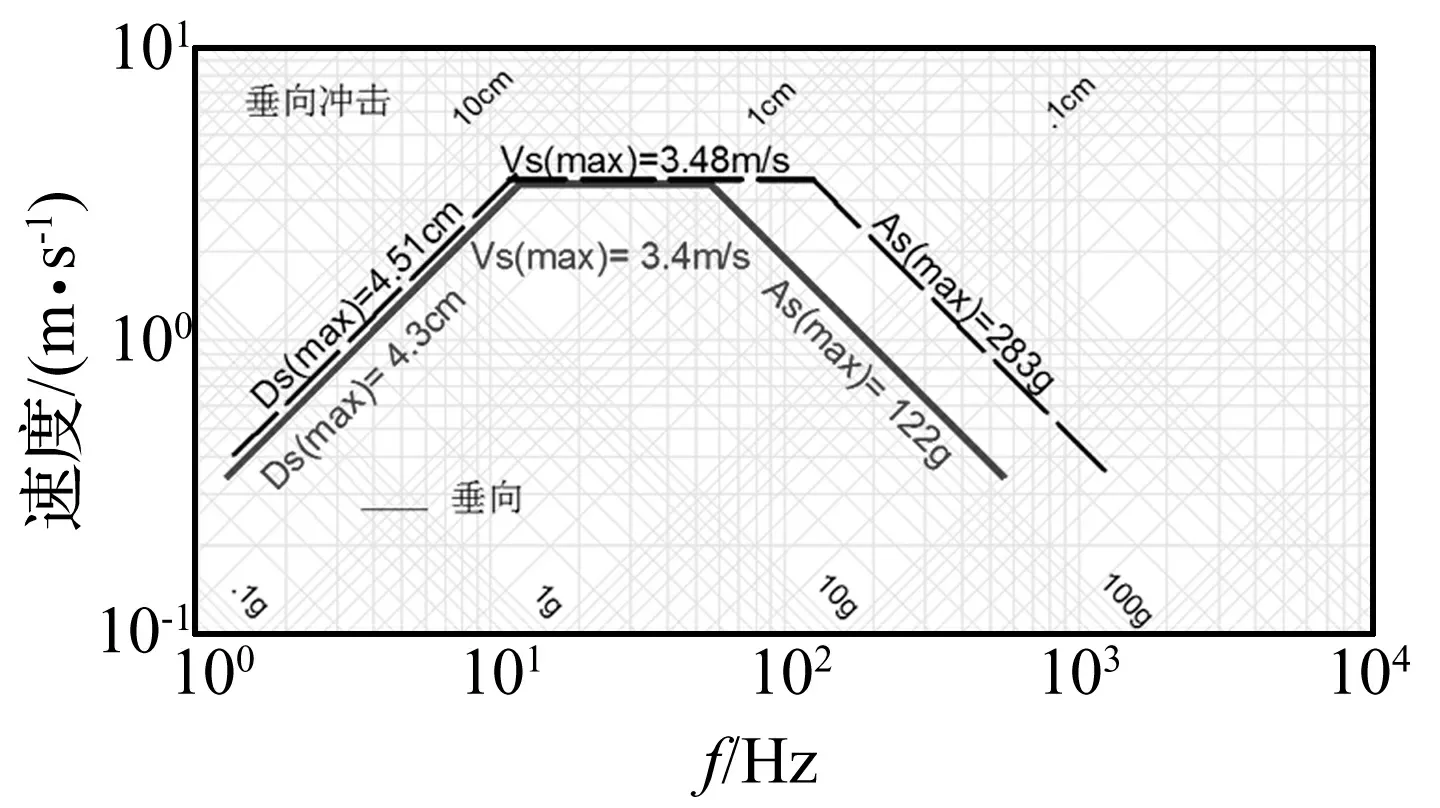
图13 锅炉基座处冲击环境
30 t设备按规范要求的冲击环境为:谱位移4.3 cm,谱速度3.4 m/s,谱加速度122 g。比较计算得到的冲击环境与规范的要求值,可以看出谱位移和谱速度与BV规范较为一致,谱加速度较大,是规范要求的2.3倍。谱加速度对应冲击输入响应的高频段,根据不同设备针对不同冲击环境输入分析,可以得到谱加速度的变化对设备响应的影响较小,设备的响应主要和低频段的谱位移及中频段的谱速度相关[14]。因此谱加速度变化对响应影响不大的设备,设计的浮动冲击平台可提供规范要求的冲击环境。
由于浮动冲击平台的内底板与外底板通过实肋板和纵桁相连接,而外底板直接受水下爆炸冲击波的作用,必然导致平台内底板响应含有较多的高频成分。为满足对安装频率和高频响应有严格要求的设备,需采取措施降低浮动冲击平台提供给设备的谱加速度。在此借鉴舰船在水下爆炸过程中的垂向滤波效应[15],多层甲板结构可对高频成分进行过滤,表现为谱加速度迅速衰减,而谱位移和谱速度衰减相对较少。根据此现象,设计和舰船甲板相类似的甲板模拟器辅助装置,如图14所示,安装于浮动冲击平台内底板之上。甲板模拟器底部的纵向连续构件与浮动冲击平台两端连接,底部与浮动冲击平台内底板保持适当间隙,来模拟实际舰船的甲板结构,其设计思路如图15所示。
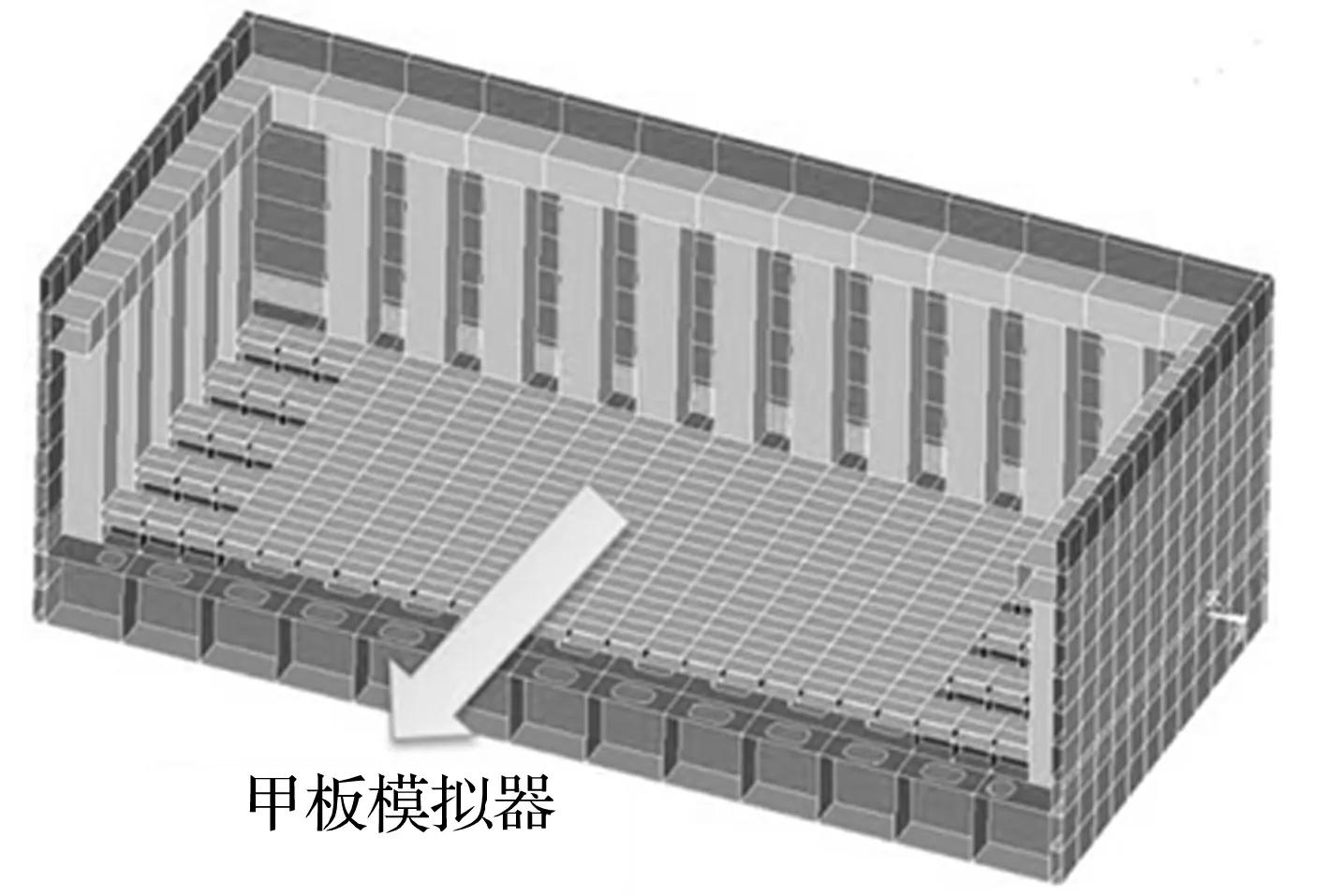
图14 内底板之上安装甲板模拟器

图15 甲板模拟器示意图
安装甲板模拟器后,可以提供弹性安装设备的安装频率,同时浮动冲击平台所提供的冲击环境中谱位移和谱速度基本不变,而谱加速度由图9所示的283 g降为185 g,出现大幅下降,基本达到设备考核要求。根据设备对安装频率及高频段谱加速度的要求情况,可安装多重甲板模拟器,来进一步调节安装频率和降低谱加速度。
4 结 论
根据美军标MIL-S-901D及德军标BV043/85,通过系统识别的方法进行了中型浮动冲击平台结构设计,主要得出如下结论:
(1) 由非线性双渐近法对浮动冲击平台在水下爆炸下的响应进行求解,计算结果与已有试验数据吻合,验证了理论方法的正确性。同时得出浮动冲击平台的响应主要为刚体运动,其冲击环境的形成主要来源于平台刚体运动,在进行平台结构设计时,需在保证强度要求的前提下,满足设备抗冲击考核的冲击环境要求。
(2) 提出的普通结构、箱形梁结构、低舷墙箱形梁结构及外板夹层箱形梁结构形式的浮动冲击平台中,低舷墙箱形梁结构及外板夹层箱形梁结构强度最好,可满足重复试验使用需要。
(3) 平台内底板的冲击环境中,谱位移与谱速度与BV规范要求较为吻合,对安装频率及谱加速度要较高要求的设备,可安装具有滤波效应的甲板模拟器来调节安装频率,同时降低高频段对应的谱加速度。
参 考 文 献
[1]边文凤,吴忠友,白光辉,等. 等效爆炸载荷下FRP船体结构的性能比较[J]. 工程力学,2012,29(增I):176-189.
BIAN Wen-feng, WU Zhong-you, BAI Guang-hui, et al. Omparison on structural performance of FRP hulls under equivalent explosion loading[J]. Engineering Mechanics, 2012, 29(Suppl I): 176-189.
[2]梁卓中,陈立贤. 应用美规MIL-STD-901D标准水中爆炸平台进行船舰重装备之抗震能力分析[J]. 科学与工程技术期刊,2009,5(2):35-50.
LIANG Zhuo-zhong, CHEN Li-xian. Heavyweight shock resistant shipboard equipment: a numerical study using an MIL-STD-901D floating shock platform[J]. Journal of Science and Engineering Technology, 2009,5(2): 35-50.
[3]李国华,李玉节,张效慈. 浮动冲击平台水下爆炸冲击谱测量与分析[J]. 船舶力学,2000,4(2):51-60.
LI Guo-hua, LI Yu-jie, ZHANG Xiao-ci. Shock spectrum measurement and analysis of underwater explosion on a floating shock platform[J]. Journal of Ship Mechanics, 2000, 4(2): 51-60.
[4]郑长允,赵鹏远,赵红光,等. 设备缓冲平台在水下爆炸载荷作用下冲击响应分析[J]. 科技导报,2012,30(18):37-40.
ZHENG Chang-yun, ZHAO Peng-yuan, ZHAO Hong-guang, et al. Shock response of buffer platform for equipment in under-water explosion[J]. Science and Technology Review, 2012, 30(18): 37-40.
[5]张玮. 利用浮动冲击平台考核舰用设备抗冲击能力的数值仿真研究[J]. 振动与冲击,2010,29(12):60-63.
ZHANG Wei. Numerical simulation for shock resistivity of shipboard equipment on floating shock platform[J]. Journal of Vibration and Shock, 2010, 29(12): 60-63.
[6]杨莉,杜俭业,杜志鹏,等. 水下爆炸冲击作用下浮动冲击平台试验安全性[J]. 噪声与振动控制,2012,6:23-25.
YANG Li, DU Jian-ye, DU Zhi-peng, et al. Security analysis for floating shock platform test subjected to underwater explosion [J]. Noise and Vibration Control, 2012, 6: 23-25.
[7]李海涛,朱锡,张振华. 水下爆炸球面冲击波作用下船体梁的刚塑性动响应特性[J]. 工程力学,2010,27(10):202-207.
LI Hai-tao, ZHU Xi, ZHANG Zhen-hua. Dynamic rigid-plastic response of ship-like beam subjected to underwater spherical shockwaves[J]. Engineering Mechanics, 2010, 27(10):202-207.
[8]MIL-S-901D (US NAVY), Military Specification: Shock Tests High Impact Shipboard Machinery, Equipment, and Systems, Requirement[S]. 1989.
[9]Zhang N, Zong Z. The effect of rigid-body motions on the whipping response of a ship hull subjected to an underwater bubble[J]. Journal of Fluids and Structures, 2011, 27:1326-1336.
[10]Li Jian, Rong Ji-li. Experimental and numerical investigation of the dynamic response of structures subjected to underwater explosion[J]. European Journal of Mechanics-B/Fluids, 2012, 32: 59-69.
[11]刘尧,刘敬喜,李天匀. 爆炸载荷作用下双向加筋方板的大挠度塑性动力响应[J]. 工程力学,2012,29(1):64-69.
LIU Yao, LUI Jing-xi, LI Tian-yun. The plastic dynamic response of two way stiffened square plates with large deflection subjected to blast loads[J]. Engineering Mechanics, 2012, 29(1): 64-69.
[12]张阿漫,戴绍仕. 流固耦合动力学[M]. 北京:国防工业出版社,2011:106-115.
[13]Kwon J I, Lee S G, Chung J H. Numerical simulation of MIL-S-901D heavy weight shock test of a double resiliently mounted main engine module[J]. Journal of the Society of Naval Architects of Korea, 2005, 42(5): 499-505.
[14]汪玉,华宏星. 舰船现代冲击理论及应用[M]. 北京:科学出版社,2005:41-60.
[15]张爱国. 大型舰船水下爆炸结构安全性研究[D]. 哈尔滨:哈尔滨工程大学,2008:66-70.

