多部件耦合包装系统逆子结构分析一般性理论
王 军, 王志伟, 卢立新, 陈安军
(1. 江南大学 机械工程学院, 江苏 无锡 214122;2. 江苏省食品先进制造装备技术重点实验室(江南大学), 江苏 无锡 214122;3. 暨南大学 产品包装与物流广东普通高校重点实验室, 广东 珠海 519070)
包装动力学经过多年的发展已形成以产品脆值与破损评价理论、包装系统动态优化设计为主要构成的新兴交叉性学科[1]。然而,传统的理论基础多是基于单自由度假设,与实际产品包装系统大都是多自由度包装系统的实际不相符合[2-4]。近年来,从耦合系统FRF反向预测部件FRF的频域逆向子结构分析方法引起了学术界的广泛兴趣。这种兴趣一方面由于部件FRF是频域子结构分析的基础,对诸如部件本身极其脆弱,或在耦合状态与自由状态存在较大差异的部件FRF往往难以通过实验的方法直接或精确测试。另一方面,来源于其在诊断和振动控制领域的巨大应用潜力是逆向子结构方法迅速发展的又一推动力。例如,对不可拆分部件在线状态的动态特性进行监控和评价,或对局部更改设计的部件的FRF辨识及耦合系统模型修正问题等。目前频域逆向子结构方法主要包括三类:逆耦合技术(Inverse Coupling Techniques) 、直接解耦技术(Direct Decoupling Techniques) 和逆子结构技术(Inverse Sub-Structuring Method)。
逆耦合技术主要是基于频域子结构的方法,通过矩阵求逆运算找到待求部件的FRF与系统水平FRF以及剩余部件FRF的关系,例如阻抗法(Impedance approach)[5-6]、导纳法(Mobility approach)[5-6]、约束力法(Constraint force approach)[7]等。直接解耦技术则基于“待求部件= 系统-剩余部件”的思想,通过构建一虚拟子系统,使其具有剩余部件相反的刚度,并且满足相容性条件和力平衡条件,通过耦合系统及虚拟子系统的动态平衡条件、界面自由度的变形协调条件、界面自由度约束力平衡条件等解析待求部件FRF[8-9]。目前亟待解决的问题主要包括,因模态截断[5]、界面连接自由度的完整性[6]、特殊频率附近的病态问题[7]等导致的不同程度的计算精度、效率和结果可靠性问题等。逆子结构方法则完全由系统水平FRF反向预测各部件FRF及部件间耦合动刚度[10-11],属于从系统水平分解到子结构水平的问题,由于避免了模态的分析与综合计算,其工程应用简便、计算高效、误差相对较低、中低频范围精度较高[12],适用于预载条件下不可拆分子结构及其耦合结构环节的动态分析,以及复杂耦合结构系统动态特性的评价和诊断。随后, Wang等[13]将逆子结构理论引入运输包装耦合系统的动态特性分析与设计,预测了主要部件水平的动态传递特性,并实验验证,初步奠定了逆子结构理论包装应用的基础。王军[14]在此基础上进一步发展了一种基于分步解耦的逆子结构分析方法,准确获取了关键部件、产品主体、运载体三个子系统的部件水平的动态传递特性。然而,这种分步解耦的方法随着部件数目的增多,测量的工作量急剧增加,效率降低,且由于累积求逆等引发误差问题,因而制约了其在多部件耦合集装化包装运输系统动态响应分析中的应用。为此,本文旨在建立多部件耦合系统逆子结构分析的一般理论方法。
1 多部件耦合系统逆子结构分析一般方法
对多部件耦合系统而言,部件水平FRF主要包含三组:从界面自由度激励到相同界面自由度响应的FRF、从界面自由度激励到内部自由度响应的FRF、从一个界面自由度激励到另一界面自由度响应的FRF,其中最后一组FRF和从界面自由度激励到内部自由度响应的FRF具有完全类似的形式,因为本质上这类FRF可归并为从界面自由度激励到内部自由度响应的FRF。
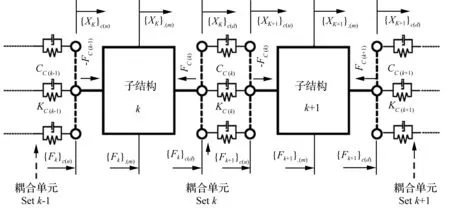
图1 多部件耦合系统
1.1 理论推导各耦合界面从耦合界面自由度激励到耦合界面自由度响应的部件水平FRF及耦合动刚度预测的逆子结构公式
一方面,对各部件隔离约束,进行单独分析,应用动力学平衡条件,得到各部件耦合点激励到响应的FRF,以第k处连接对应的两部件为例,可以很容易得到:
(1)
类似的方程组总共有N-1个,其中c(u),c(d)为第k处耦合两部件耦合点。
由此可解得:
(2)
另外,对于耦合系统,列出其运动学方程,
{Xs}=[Hs]{Fs}
(3)
由式(3)得到
(4)
比较式(2)、式(4),[g1]只包含部件水平FRF及耦合动刚度,[g2]只包含系统水平FRF,据此可以解得各耦合界面从耦合界面自由度激励到耦合界面自由度响应的FRF及耦合动刚度预测的逆子结构公式。
1.2 理论推导从界面自由度激励到内部自由度响应的部件水平FRF预测的逆子结构公式
对于从界面自由度激励到内部自由度响应的部件水平FRF计算,需要结合动态子结构预测公式,利用上述已求得的部件水平FRF及耦合动刚度,解析出待求的部件水平FRF。为此,可以首先由(3)式,将其表示为各部件FRF、激励外力、耦合点FRF及约束反力的关系:
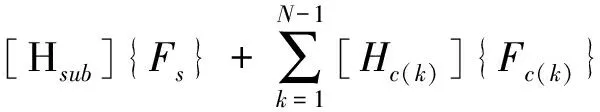
(5)
其中,
(6)
由位移协调条件和力平衡条件得到各耦合点约束反力Rc(k):
{Rc(k)}=[Kc(k)]({Xk+1}c(u)-{Xk}c(d))
(7)
其中,[Kc(k)]表示动刚度,将各耦合点处的约束反力矩阵{Rc}({Rc}是各处{Rc(k)}组成的整体。)表示为激励外力,并用部件水平FRF及耦合动刚度表达转换矩阵[R]:
{Rc}=[R]{Fs}
(8)
综上式(5)~式(8),得到系统水平FRF与部件FRF及耦合动刚度的关系
[Hs]=f([Hsub],[Hc],[Kc])
(9)
由式(9)进行矩阵求逆运算,并结合上述求得的部件水平FRF及耦合动刚度,可得到从界面自由度到内部自由度的部件水平FRF预测的逆子结构公式。
式(9)本质上为多部件耦合系统子结构分析的一般化公式,也是获取多部件耦合系统逆子结构分析计算公式的关键。
不失一般性,以图1所示的任意多部件耦合系统为例,导出系统FRF与部件FRF的映射关系。
对于多部件耦合系统而言,其运动学方程可写作:
(10)
将式(8)展开,即:
{Rc}={Rc(1)…Rc(k)…Rc(N)}T
(11)
[R]={[R1] … [Rk] … [RN]}T
(12)
据此,可以得到各耦合点约束反力和外力的映射关系,
{Rc(k)}=[Rk]{Fs}
(13)
将(13)式代入(10)式,由(10)式求解各处位移响应,并将其代入(7)式,得
[A]{Rc}=[B]{Fs}
(14)
其中,
(15)
(16)
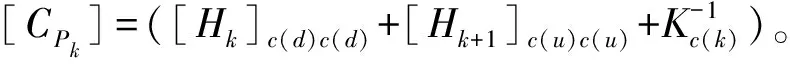
据此,可以得到转换矩阵[R],即:
[R]=[[R1]…[Rk]…[RN]]T=[A]-1[B]
(17)
将式(17)代入式(7)再代入式(10),可得到系统FRF与部件FRF的映射关系。
2 算例
以四部件单点耦合系统为例,按照上述解法求解从系统水平FRF反向计算部件水平FRF及部件间耦合动刚度的逆子结构理论公式。

图2 四部件单点耦合系统模型
首先,由(1)~(4)式得:
(18)
(19)

(20)
(21)

(22)
(23)
再由两部件耦合系统逆子结构方法[6],得到:
(24)
(25)
(26)
将式(18)~(26)代入(10) 式,得:
HA,o(a)c1(a)=
(27)
(28)
(29)
HD,c3(d)i(d)=
(30)
其中,
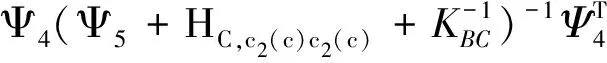
(31)
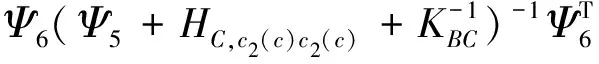
(32)
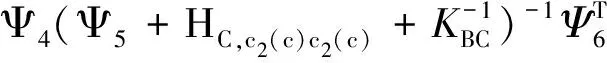
(33)
(34)
(35)
(36)
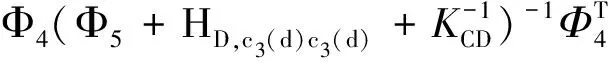
(37)
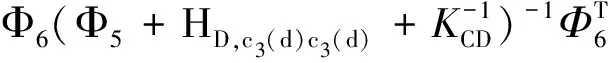
(38)
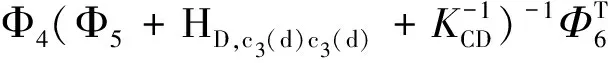
(39)
(40)
(41)
3 数值仿真
采用集总参数模型验证上述理论,模型如图3所示,模型参数见表1。将系统划分为A,B,C,D四个部件,如图所示。
分别计算系统传函及各部件传函,应用(18)~(42)式计算A,B,C,D四个部件的部件水平FRF及部件间耦合连接的动刚度,并将结果与直接计算的部件水平FRF对比,预测值与给定值完全吻合,如图4所示,从而验证了所建立理论的正确性。
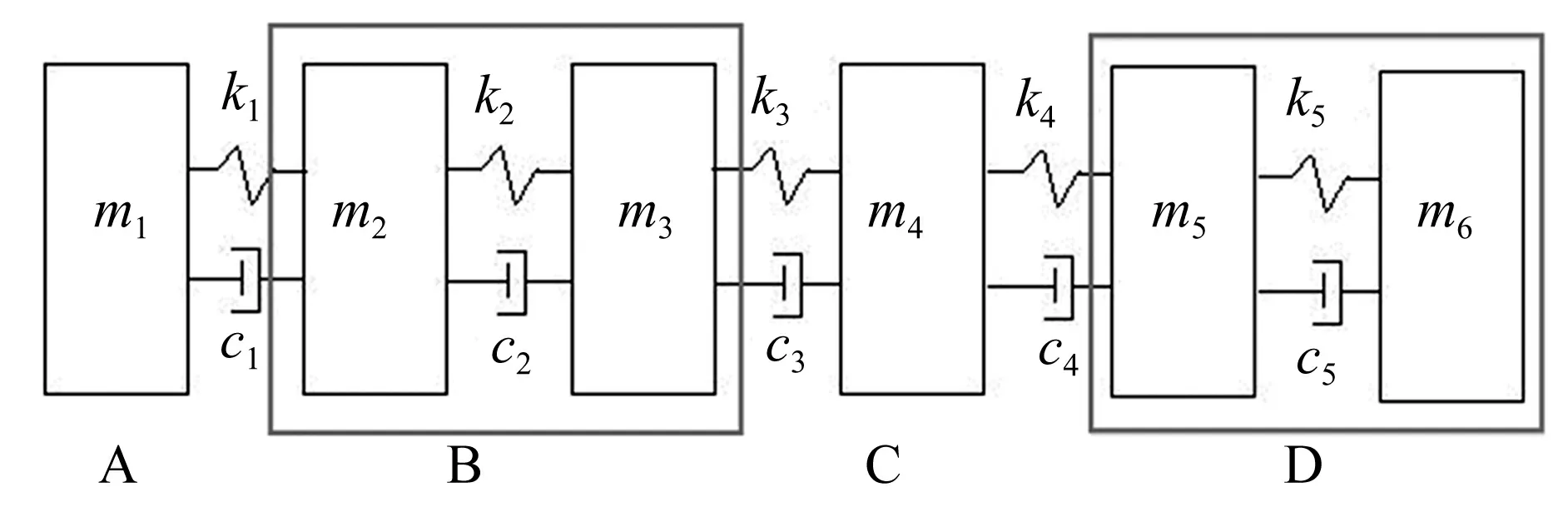
图3 集总参数模型

表1 集总参数模型参数

图4 部件水平传递函数及耦合界面动刚度预测值与计算值对比
4 结 论
建立了多部件耦合系统逆子结构分析的一般方法,得到了从系统水平传函反向计算各耦合部件传函及部件间耦合动刚度的理论公式,采用集总参数模型验证了所建立理论的正确性,研究结果对多部件耦合包装系统的动态特性分析具有一定价值。
(1) 基于子结构理论,提出了一种由系统水平传函反向预测部件传函的逆子结构分析一般方法;
(2) 采用集总参数模型对所建立的方法进行了数值验证。
参 考 文 献
[1]王军, 卢立新, 王志伟. 产品破损评价及防护包装力学研究[J].振动与冲击, 2010, 29(8):43-45.
WANG Jun, LU Li-xin, WANG Zhi-wei. Product damage evaluation and protective packaging dynamics[J]. Journal of Vibration and Shock, 2010, 29(8):43-45.
[2]高德, 卢富德. 聚乙烯缓冲材料多自由度跌落包装系统优化设计[J].振动与冲击, 2012, 31(3):69-72.
GAO De, LU Fu-de. Optimization design of MDOF package cushioning system made of polyethylene[J]. Journal of Vibration and Shock, 2012, 31(3):69-72.
[3]张连文,杨传民,孟宪文,等. 圣女果运输包装件振动冲击性能实验研究[J].振动工程学报,2011,24(1): 73-77.
ZHANG Lian-wen, YANG Chuan-min, MENG Xian-wen, et al. Vibration and impact performance tests of saint fruit transport packages [J]. Journal of Vibration Enginnering, 2011, 24(1): 73-77.
[4]王军, 卢立新, 王志伟. 三次非线性多层堆码包装系统关键部件三维组合冲击谱研究[J].振动与冲击, 2011, 30(1):188-190.
WANG Jun, LU Li-xin, WANG Zhe-wei. 3-D combined shock response spectrum of a cubic nonlinear stacked packaging system with critical components[J]. Journal of Vibration and Shock, 2011, 30(1): 188-190.
[5]D’Ambrogio W, Fregolent A. Decoupling of a substructure from modal data of the complete structure [C]. Proceedings of ISMA 2004-International Conference on Noise and Vibration Engineering, Leuven, Belgium, 2004.
[6]D’Ambrogio W, Fregolent A. Promises and pitfalls of decoupling techniques [C]. Proceedings of the Twenty Sixth International Modal Analysis Conference, Bethel, 2008.
[8]Voormeeren S N, Rixen D J. A family of substructure decoupling techniques based on a dual assembly approach [J]. Mechanical Systems and Signal Processing, 2012, 27: 379-396.
[9]D’Ambrogio W, Fregolent A. The role of interface DoFs in decoupling of substructures based on the dual domain decomposition[J]. Mechanical Systems and Signal Processing, 2010, 24(7): 2035-2048.
[10]Zhen J, Lim TC, Lu G. Determination of system vibratory response characteristics applying a spectral-based inverse sub-structuring approach. Part I: analytical formulation [J]. International Journal of Vehicle Noise and Vibration, 2004, 1(1/2): 1-30.
[11]Zhen J, Lim TC, Lu G. Determination of system vibratory response characteristics applying a spectral-based inverse sub-structuring approach. Part II: motor vehicle structures [J]. International Journal of Vehicle Noise and Vibration, 2004, 1(1/2): 31-67.
[12]Cloutier D, Avitabile P. Investigation on the Use of Various Decoupling Approaches [C]. Proceedings of the IMAC-XXVIII, Florida, USA, 2010.
[13]Wang ZW, Wang J, Zhang YB, et al. Application of the inverse substructure method in the investigation of dynamic characteristics of product transport system [J]. Packaging Technology and Science, 2012, 25(6): 351-362.
[14]王军. 产品破损评价及其防护包装动力学理论研究 [D]. 无锡: 江南大学, 2009.

