基于小波降噪和短时傅里叶变换的主轴突加不平衡非平稳信号分析

胡振邦, 许睦旬, 姜歌东,2, 张东升

(1.西安交通大学 机械工程学院，西安 710049; 2.西安交通大学 机械制造系统工程国家重点实验室，西安 710049)

现代制造业向着高速高效的方向不断发展，装备制造起着至关重要的决定性作用，电主轴是高速加工工艺中最为主要的核心部件，其工作性能将直接影响到装备制造的水平[1]，由此可见，通过各种技术手段提高电主轴工作性能指标具有极其重要的意义[2]。由于材质、加工误差、安装误差等多种因素导致的主轴不平衡是电主轴最为常见的故障，通过改善电主轴不平衡状态能够有效提高电主轴加工精度[3-4]，因此，主轴动平衡技术越来越受到人们的关注。目前，主轴在线动平衡技术大多采用试重的方式用来确定主轴失衡量与振动响应之间的关系[5-6]，对主轴在线添加试重可视为对主轴突加不平衡，由此可以改变主轴振动响应状态，造成主轴振动信号变化，此过程的振动信号具有极其明显的非平稳性，并且由于电主轴结构复杂，多种噪声信号混杂其中，很难从测量信号中直接判断主轴运行状态，传统的傅里叶变换难以对这种含有大量噪声的非平稳信号进行分析[7]。基于此种情况，本文提出一种采用小波降噪和短时傅里叶变换相结合对主轴突加不平衡非平稳信号进行分析处理的方法，通过小波降噪对原始测量信号按目标频带进行分解，提取转频信号所在的频带进行信号重构，再利用短时傅里叶变换对重构信号进行分析，提取转频信号的振动幅值信息。

1 小波降噪技术

1.1 谐波小波基本原理

小波变换是一种具有明确的时域、频域函数的复变换，谐波小波最早由Newland[8]提出，该方法相较于其他小波算法具有算法简单、锁相功能好、适用范围广等优点[9-10]，并且能够适用于非平稳信号的处理，谐波小波时域对应的函数实部为偶函数，虚部为奇函数，即偶函数和奇函数都是零相滤波器，由此可以判断谐波小波具有“锁定”信号相位的能力，这种特点对于主轴振动信号的特征提取具有十分重要的作用。

1.2 谐波小波滤波与信号重构

在实际应用中，为了得到频率为2πm≤ω≤2πn范围内的信号，需要对谐波小波进行伸缩和平移，此时谐波小波的函数如下所示[11]：

(1)

其中m，n决定了谐波小波变换的尺度j。

对于实际信号x(t)相对尺度j的谐波小波变换如下所示：

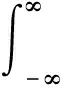
(2)

Wx(m,n,τ)=X(ω)Wm,n(ω)

(3)

信号x(t)在尺度j下的谐波小波变换过程如图1所示。

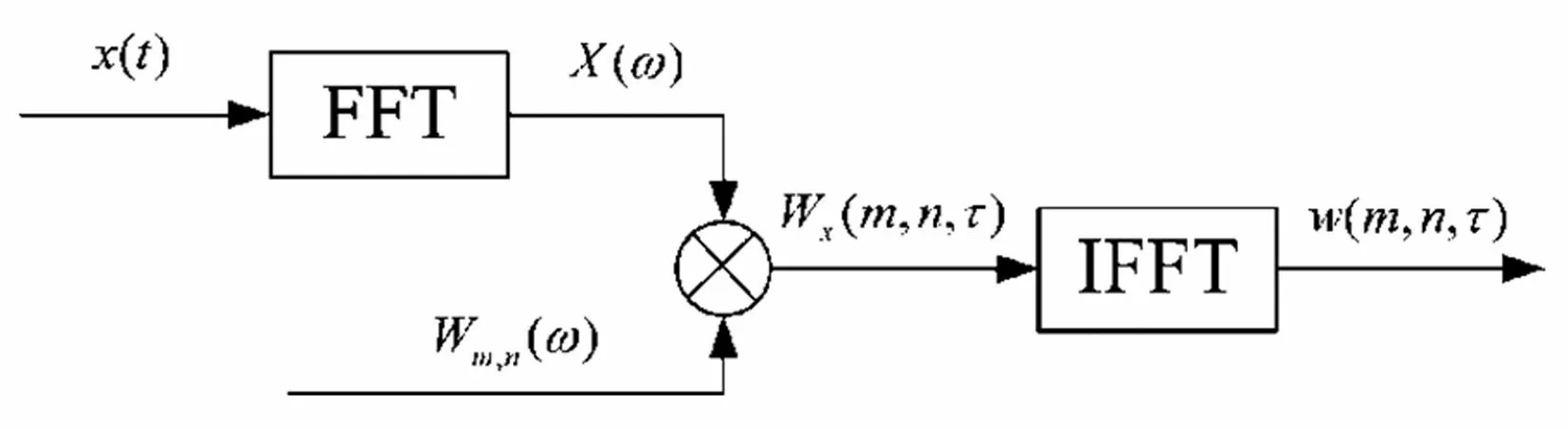
图1 谐波小波变换过程

利用谐波小波在频域的优良特性，在不同分解层和同一层上的不同频段的局部频谱进行细化分析，并对信号进行重构，得到转频信号所在频带范围的还原信号。

1.3 滤波效果分析

主轴运行过程中的信号极为复杂，以转频信号为主同时伴有多种倍频信号，突加不平稳时的信号中转频信号会发生非线性变化，假定主轴转速为1 500 r/min，采样频率为2 048 Hz，采样时间为1 s，以如式(4)形式的信号作为仿真信号：

x(t)=x1(t)+x2(t)+x3(t)

(4)

其中x1(t)=3*e-2t*sin(2π*25*t)为变化的转频信号，x2(t)=2*sin(2π*150*t)为6倍频谐波信号，x2(t)=4*sin(2π*250*t)为10倍频谐波信号，仿真信号x(t)的时域波形及频谱特性如图2所示。

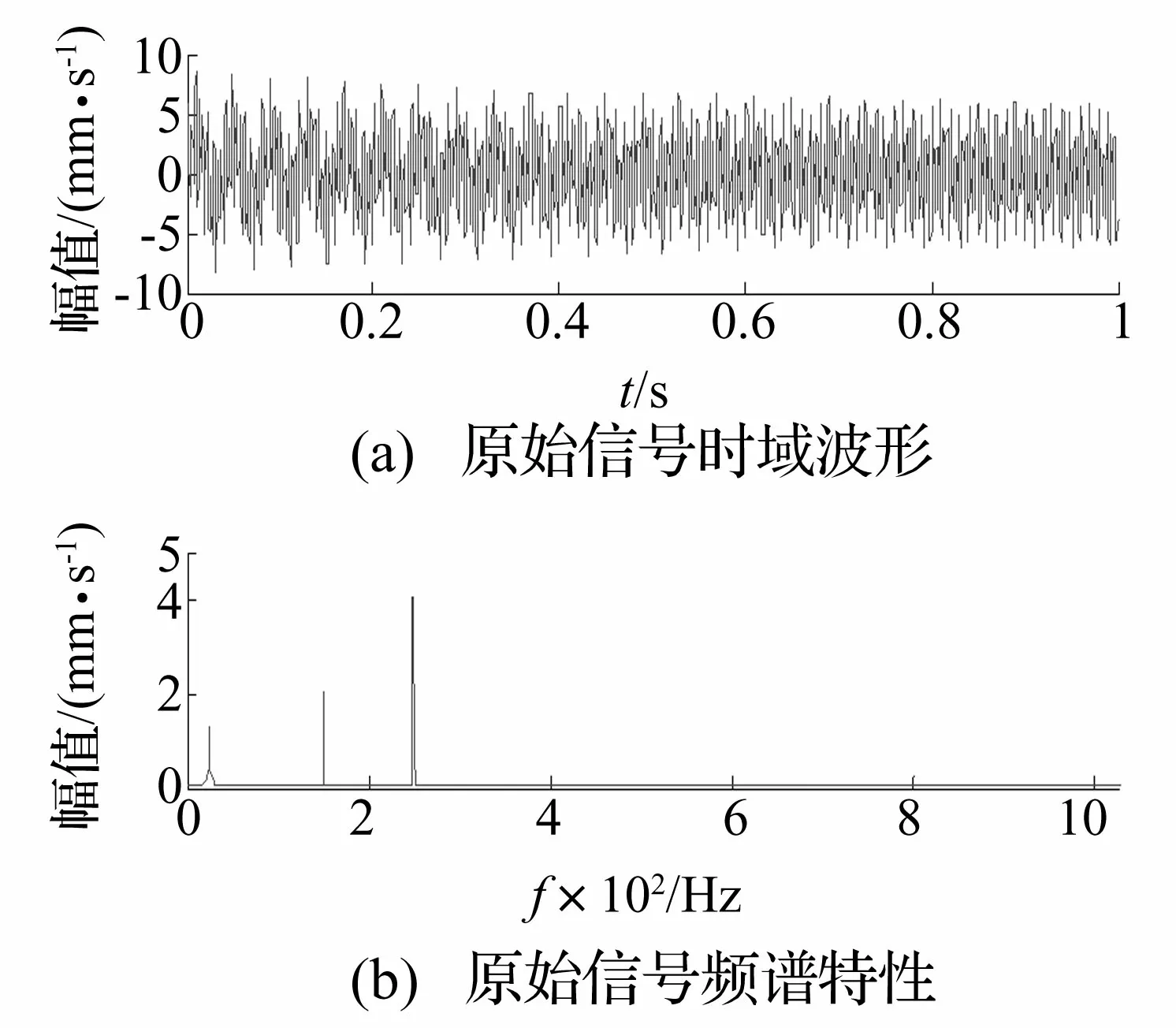
图2 仿真信号时域波形及频谱特性图

可见，由于信号中存在大量的倍频信号，已经无法从时域波形中将转频信号进行准确提取，从频谱特性图中可以提取到转频信号的幅值，然而利用傅里叶变换得到的转频信号幅值是定值，而该幅值实际上是随时间变化的，因此频谱特性图无法准确反映出信号的幅值变化过程，对该信号进行谐波小波变换并对转频及倍频信号进行重构后所得的时域波形及频谱分析结果如图3所示。

由图3可以看出，利用谐波小波可以清晰的将转频信号从原有信号中分离出来，重构的转频信号具有非线性特征，与仿真信号的基本特征相吻合，实现了对于高次谐波信号的滤除，同时采用谐波小波技术可以将不同频域范围内的倍频信号根据需要进行分离重构，可见传统的傅里叶变换方法仅能够对平稳信号的频谱进行分析，而对于非平稳信号的分析能力还有待提高。

图3 信号分离并重构后的信号

2 短时傅里叶变换

目前在工程应用领域，对于信号的频谱分析一般都采用快速傅里叶变换的方法，该方法的应用最为广泛，技术也相对比较成熟，但是快速傅里叶变换方法无法满足非平稳信号的分析，对非平稳过程进行分析时存在无法避免的缺陷[12]，由于快速傅里叶变换只能给出时域或频域内的统计平均结果，而不能提供信号时域和频域局部化的信息，因此采用短时傅里叶变换的方法来克服快速傅里叶变换的不足之处，进而为主轴振动特性分析提供准确可靠的信息[13]。短时傅里叶变换的基本运算公式如下：

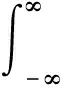
(5)

其中gω,τ(t)=g(t-τ)e-jωt为积分核函数，e-jωt为限频函数，g(t-τ)为限时函数，Gx(ω,τ)则是反映x(t)在τ时刻频率为ω信号频率成分。

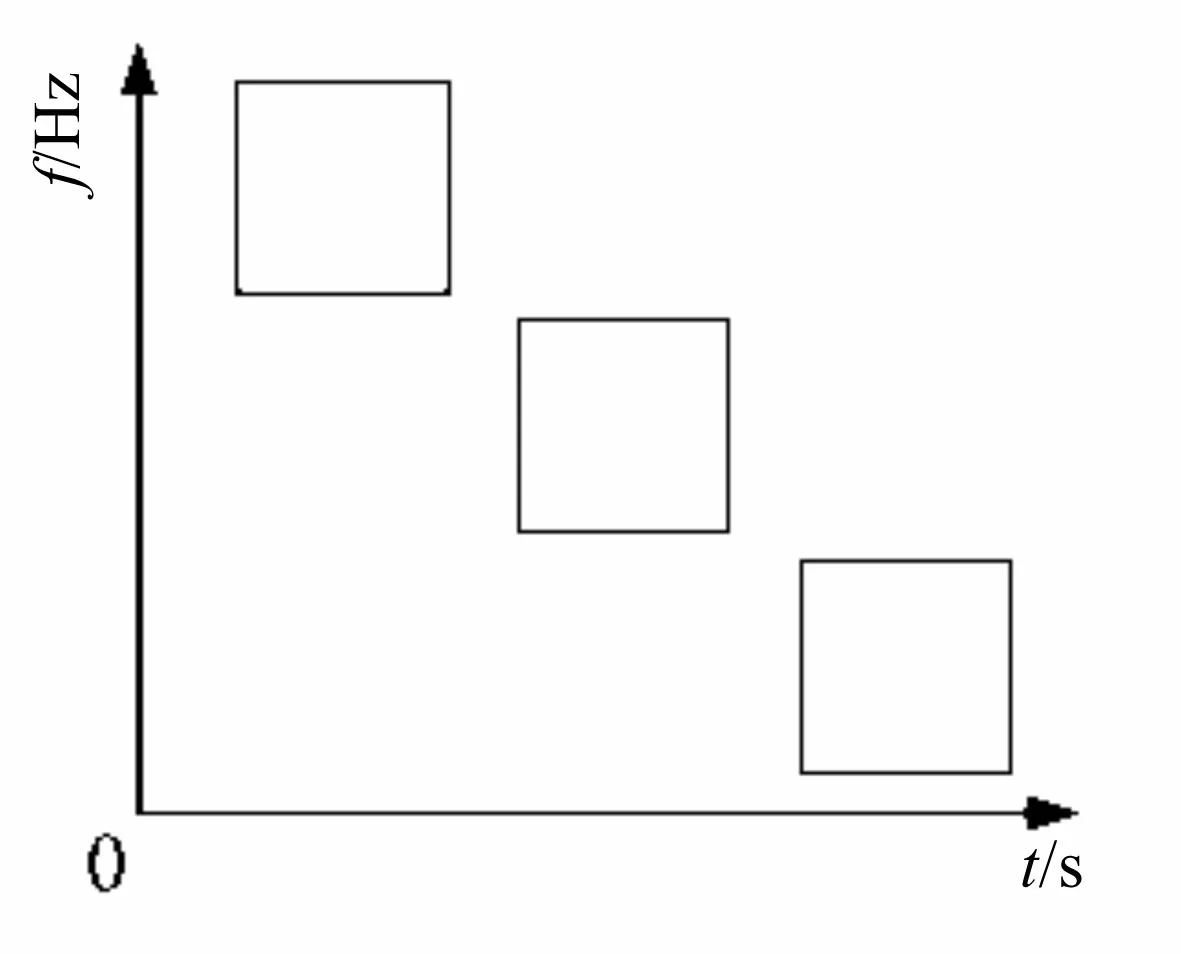
图4 短时傅里叶变换基本原理示意图

由此可以看出，短时傅里叶变换是通过固定的时域窗函数g(t-τ)对目标函数x(t)进行截取，对于截取的局部时域信号进行傅里叶变换，通过改变时窗的起始时刻t来调整时域窗函数g(t-τ)的位置，进而得到以t为变化过程的一系列傅里叶变换结果，由这些结果所构成的集合即是短时傅里叶变换的时频联合分析结果。

以仿真信号x(t)中1 500 r/min的转频信号x1(t)=3*e-2t*sin(2π*25*t)为例，利用短时傅里叶变换计算该振动信号幅值，选用矩形窗函数，窗宽256，移动步长为1，分析结果如图5所示。

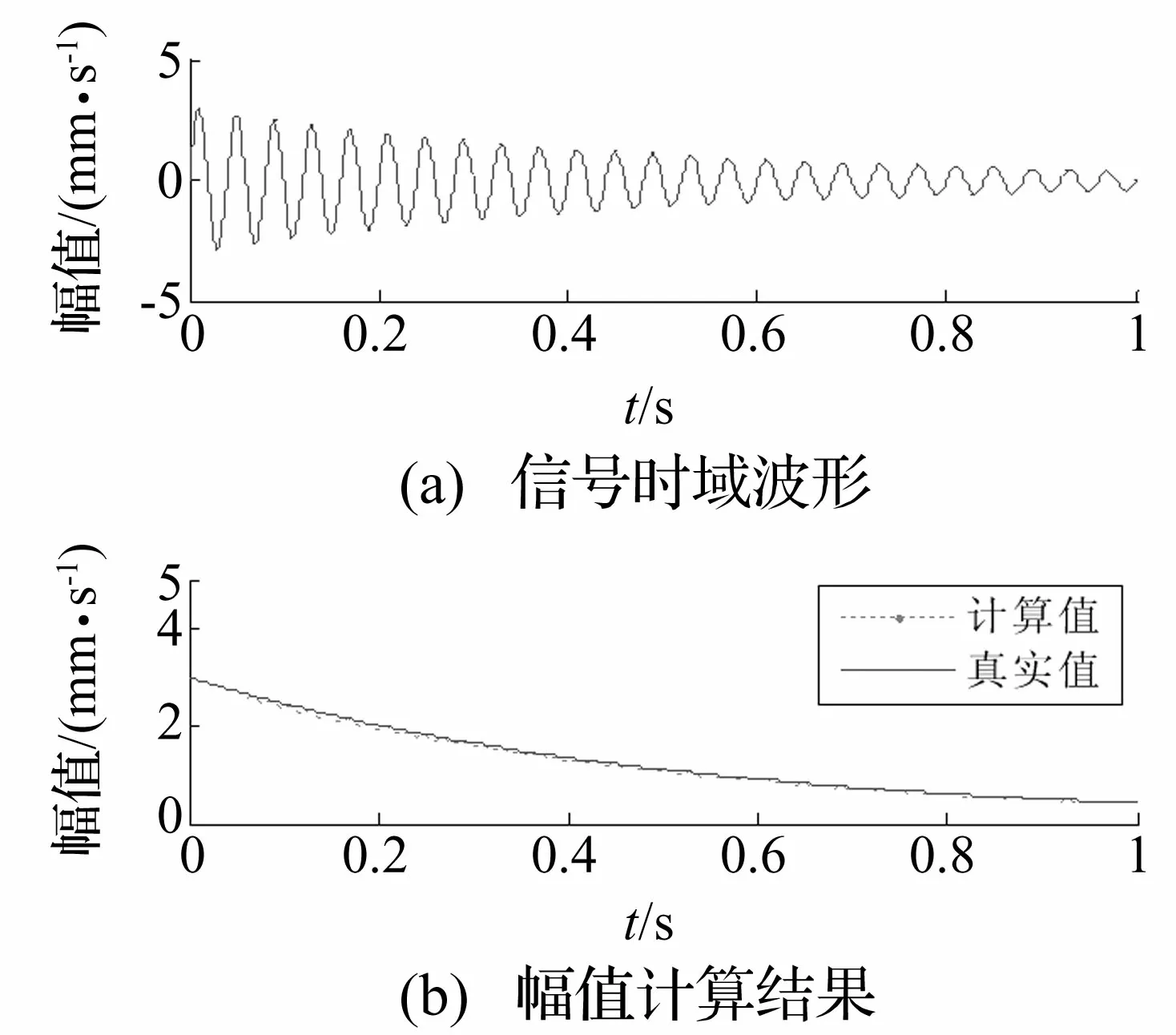
图5 短时傅里叶变换计算幅值

图6 振动测试试验台

从图5可以看出，采用短时傅里叶变换能够对非平稳信号的幅值进行计算，计算值与真实值非常接近，基本满足应用需要，由此可以知道利用固定时窗函数进行短时傅里叶变换，时域内和频域内都有较好的局部性，适合对非平稳信号进行分析。

3 应用实例

为验证本文提出的方法的可行性，采用现有电主轴在线动平衡实验平台对方法进行验证，实验现场如图6所示。

该实验平台采用150SD40Q7型电主轴，最高设计转速可达30 000 r/min，最大功率为7 kW，利用在线式动平衡装置[14]在主轴平稳运行过程中添加不平衡量，利用振动加速度传感器对主轴振动信号进行测量并换算为振动速度进行处理，振动加速度的测量采用PCB公司的352C33型ICP振动加速度传感器，信号采集卡采用NI公司出品的4472多路同步信号采集卡，分辨率为24位，实验用系统采样频率为10 kHz，采样时间为4 s，电主轴测试转速设定为3 000 r/min。

测试信号的原始时域波形图如图7(a)所示，经过傅里叶变换后的频谱分析结果如图7(b)所示，可见，在主轴突加不平衡的测试信号中已无法直观分辨出转频信号，同时，由于存在大量的高倍频信号和多种噪声的干扰，导致不能够通过时域波形和频谱分析结果看出转频信号的幅值变化情况，无法在动平衡过程中准确判定主轴振动变化情况。

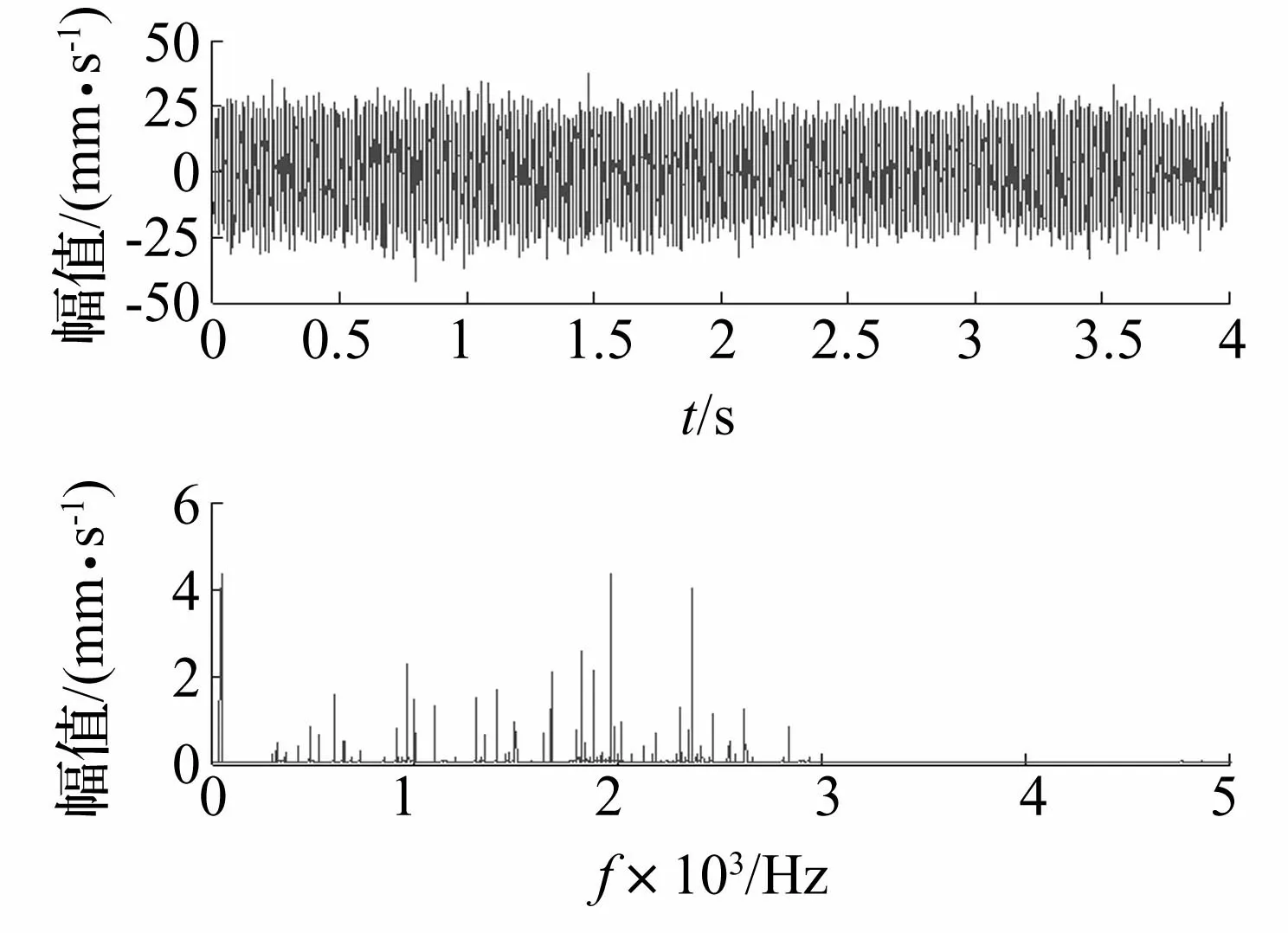
图7 突加不平衡测试信号时域波形频谱

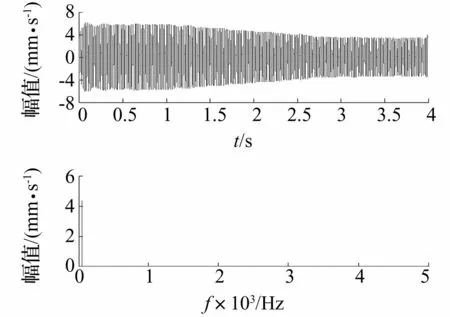
图8 重构的转频信号时域波形及频谱

利用谐波小波分析对测量信号进行滤波处理，并对转频信号进行重构后的信号时域波形如图8所示，从时域波形可以看出转频信号是随时间变化的，而通过傅里叶变换无法准确表达出转频信号的幅值变化情况。

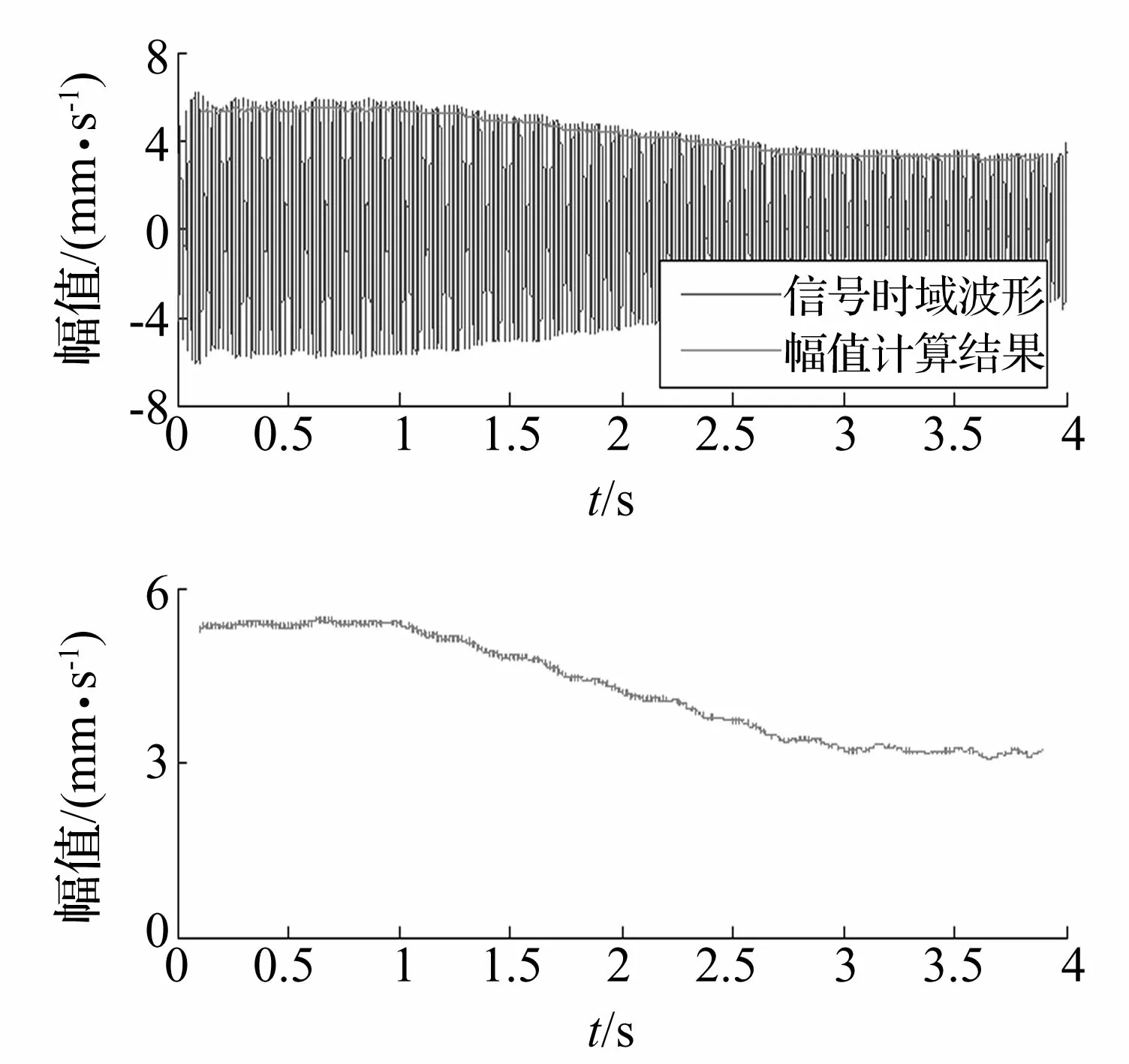
图9 短时傅里叶变换计算的转频信号幅值

选取短时傅里叶变换的时窗宽度为2048，移动步长为1，得到如图9所示的幅值计算结果。

从实验结果可以看出，从第1秒开始主轴转频振动幅值随时间推移而不断的减小并呈现出非平稳变化趋势，，当到达第3秒时振动幅值逐渐趋于平缓，通过短时傅里叶变换可以准确计算出振动幅值，取得了良好的实验结果。

4 结 论

主轴平稳运行过程中，突加不平衡将产生非平稳振动信号，并且信号中含有大量的倍频信号和噪声信号干扰，无法通过传统的傅里叶变换对信号进行准确分析，本文对这类问题进行了研究，得到如下结论：

(1)本文提出一种基于小波降噪和短时傅里叶变换相结合对主轴非平稳振动信号进行分析处理的方法，该方法利用谐波小波技术可以将转频信号利用时频分析的方法从原始信号中分离出来并进行信号的重构，实现了突加不平衡非平稳信号的消噪，还原了转频信号的变化过程。

(2)采用短时傅里叶变换对降噪后的转频信号进行分析计算，获取转频信号振动幅值，能够直观、清晰地反映主轴振动幅值变化情况。

(3)该信号处理方法可为在线式动平衡装置在动平衡调整过程中准确监测振动变化情况提供预警参考，避免不平衡调整量添加过量而导致主轴振动的骤增变化，可以防止由此而发生的主轴严重运行故障。

在实际应用过程中，应根据现场需要适当调整短时傅里叶变换的窗函数及移动步长等参数，合理控制算法的计算量，提高应用效率。

参 考 文 献

[1]吴玉厚.数控机床电主轴单元技术[M].北京:机械工业出版社,2006.

[2]Rodrigues D J, Champneys A R, Friswell M I, et al. Automatic two-plane balancing for rigid rotors[J]. International Journal of Non-Linear Mechanics,2008,43(6): 527-541.

[3]LIAO Yu-he, LANG Gen-feng, WU Fang-ji,et al.An improvement to holospectrum based field balancing method by reselection of balancing object[J]. Journal of Vibration and Acoustics, Transactions of the ASME, 2009,131(3): 0310051-0310057.

[4]ZHANG Yun, ZHANG Dong-sheng, XU Mu-xun, et al. Research on accuracy improvement of holospectrum technique in machine tool spindle[J]. Advances in Communication Technology, 2011, 4:598-603.

[5]Zhou S Y, Dyer Stephen W, Shin K K, et al. Extended influence coefficient method for rotor active balancing during acceleration[J]. Journal of Dynamic Systems, Measurement and Control, Transactions of the ASME, 2004,126(1): 219-223.

[6]章 云,梅雪松,邹冬林,等.应用模态分析及傅里叶变换的柔性转子无试重动平衡方法[J].振动与冲击,2008, 31(11):7-10.

ZHANG Yun，MEI Xue-song, ZOU Dong-lin. A field balancing method of a flexible rotors based on modal analysis and fourier transformation[J]. Journal of Vibration and shock, 2008,31(11): 7-10.

[7]张 鹏,孟 光,吴峰崎.小波分析降噪方法在碰磨和突加不平衡信号特征提取中的应用[J].汽轮机技术,2005, 47(6):441-443.

ZHANG Peng, MENG Guang, WU Feng-qi. The application of wavelet denoising method in the fault feature extraction of friction and sudden unbalance signal[J]. Turbine Technology,2005,47(6): 441-443.

[8]Newland D E. Harmonic wavelet analysis[J]. Proceeding of Royal Society of London, 1993, 443(10):203-205.

[9]孙 伟,熊邦书,黄建萍,等.小波包降噪与LMD相结合的滚动轴承故障诊断方法[J].振动与冲击,2012,31(18):153-156.

SUN Wei，XIONG Bang-shu，HUANG Jian-ping, et al. Fault diagnosis of a rolling bearing using wavelet packet de-noising and LMD[J]. Journal of Vibration and shock, 2012,31(18):153-156.

[10]李 辉,郑海起,唐力伟.基于改进双树复小波变换的轴承多故障诊断[J].振动、测试与诊断,2013,33(1):53-59.

LI Hui, ZHENG Hai-qi, TANG Li-wei. Bearing multi-faults diagnosis based on improved dual-tree complex wavelet transform[J]. Journal of Vibration, Measurement & Diagnosis,2013,33(1): 53-59.

[11]胡广书.现代信号处理教程[M].北京:清华大学出版社,2004.

[12]赵凤展,杨仁刚.基于短时傅里叶变换的电压暂降扰动检测[J].中国电机工程学报, 2007,27(10):28-34.

ZHAO Feng-zhan, YANG Ren-gang.Voltage sag disturbance detection based on short time fourier transform[J]. Proceedings of the CSEE, 2007,27(10),28-34.

[13]胡晓依,何庆复,王华胜,等.基于STFT的振动信号解调方法及其在轴承故障检测中的应用[J].振动与冲击,2008,27(2):82-86.

HU Xiao-yi, HE Qing-fu, WANG Hua-sheng, et al. Vibration signal demodulation method based on STFT and its application in rolling bearing fault detections [J].Journal of Vibration and shock, 2008,27(2):82-86.

[14]章 云,梅雪松,胡振邦,等.注液式高速切削主轴动平衡装置设计及其性能研究[J].西安交通大学学报,2013, 47(3):13-17.

ZHANG Yun, MEI Xue-song, HU Zhen-bang, et al. Design and performance analysis of hydrojet-typed balancing device for high-speed machine tool spindle[J].Journal of Xi’an Jiaotong University,2013,47(3):13-17.