型钢混凝土框架结构失效模式的识别和优化

郑山锁， 孙龙飞， 司 楠， 杨 威， 秦 卿

(西安建筑科技大学 土木工程学院，西安 710055)

我国地处环太平洋地震带与欧亚地震带之间，人口密集，财富聚集，地震灾害时常发生，造成了大量的人员伤亡和财产损失。在历次地震灾害中，尤其是罕遇地震中，建筑结构的破坏与倒塌均造成巨大的灾难[1]。大量研究表明，建筑结构倒塌的主要原因是结构薄弱层破坏、结构出现柱铰破坏等不理想的失效模式造成结构不能继续承受较大的水平地震作用和竖向荷载。结构在地震作用下的失效模式数量会随着结构构件数量和冗余度的增加而成倍增加[2]，准确地识别结构的主要失效模式，是控制和优化结构抗震性能的前提和关键。欧进萍等[3]提出“最弱失效模式”的概念，即在众多失效模式中，仅有少数几个失效模式对结构体系可靠度起主要作用。基于“最弱失效模式”理论，孙爱伏等[4]提出高层钢结构的地震失效模式控制可以采用加强薄弱构件的方法实现；白久林等[5]基于IDA方法对混凝土结构失效模式进行了优化分析。

随着高层和超高层建筑的兴起，型钢混凝土结构因其强度高、刚度大等优点，得到了广泛的应用，但目前对于此类结构的地震失效模式和抗震性能研究还比较少。鉴于此，本文采用OpenSEES软件基于IDA方法对型钢混凝土框架结构地震失效模式进行了比较系统的研究，提出了结构失效模式的识别及优化方法，对相应工程应用有一定的理论指导意义。

1 增量动力分析方法(IDA)

增量动力分析(Incremental Dynamic Analysis，简称IDA)方法是逐步增量的动力参数化分析方法，现已广泛应用于基于性能的结构抗震分析中。吴巧云等[6]基于IDA方法对钢筋混凝土框架抗震性能进行了分析。其基本思想是对结构施加一条或者多条地震动，使用不同的调幅原则和调幅系数不断增大每条地震动记录的幅值IM(Intensity Measure)，在不同的IM作用下对结构进行非线性动力分析，可以得到不同的结构损伤指标DM(Damage Measure)，这样形成了一条或者多条IM-DM曲线(即IDA曲线)。IDA分析能够记录结构在地震作用下从弹性到弹塑性直到结构倒塌破坏全过程中的反应[7]，便于通过考查结构倒塌破坏过程中每个构件的强度和变形发展，找出结构的薄弱环节，可为结构失效模式的识别和优化提供有效的途径。

2 结构有限元模型

根据《建筑抗震设计规范》(GB50011-2010)和《型钢混凝土组合结构技术规程》(JGJ138-2001)，采用通用结构设计软件PKPM，设计了一榀15层3跨的型钢混凝土框架结构。框架结构的平面尺寸如图1所示，并取其中一榀框架进行有限元建模分析，结构构件单元编号见图2。结构底层层高4.2 m，其他层层高均为3.6 m，结构总高度为54.6 m，楼板厚度均为120 mm。框架楼面恒载取5.0 kN/m2，活荷载取2.0 kN/m2，屋面恒载取5.0 kN/m2，活荷载取0.5 kN/m2。一至五层梁、柱混凝土强度等级为C40，六至十层梁、柱混凝土强度等级为C35，十一至十五层梁、柱混凝土强度等级为C30，其他构件的混凝土材料强度均为C30。型钢均采用Q235钢，梁、柱主筋采用HRB335，箍筋采用HPB235，结构尺寸及配筋见表1。设计地震烈度为8度(0.2 g)，地震分组为第一组，场地类别为Ⅱ类，抗震等级为二级。利用OpenSEES软件建立结构的有限元模型，恢复力模型采用纤维模型，混凝土本构采用Concrete02模型，钢材本构采用Steel02模型，单元采用非线性梁柱单元。

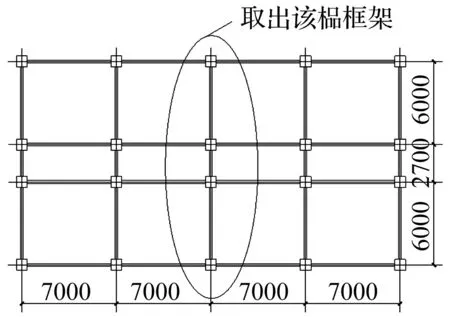
图1 结构平面图

3 地震波选取

本文选择典型的强震记录，即按照由反应谱的两个频率段控制法选波[8]，从美国太平洋地震研究中心PEER数据库中选取了10条相关的地震记录，作为本文IDA分析的地震动输入，具体参数见表2。

4 单条IDA曲线的生成方法

本文以EE1-Kobe地震波为例，简要介绍单条IDA曲线的生成方法。采用最大层间位移角θmax作为结构反应参数，峰值加速度PGA作为地震动强度参数，计算时通过调幅系数得到一系列不同的地震动强度。具体过程如下：用原始的加速度值α乘以调幅系数λ得到第一次输入加速度α1，采用α1对结构进行弹塑性动力时程分析，记录最大层间位移角θmax；第二次分析时用hunt&fill算法[9]进行调幅，用调幅后的加速度α2再对结构进行弹塑性动力时程分析，记录最大层间位移角θmax，直到出现数值发散，表明结构已经倒塌。此时，停止调幅，对较低的PGA值进行中间插值，以便有足够多的点进行插值，再使用Matlab工具箱中的三阶样条对所有点插值得到EE1地震记录的IDA曲线。第一次分析时取PGA=0.5 g，调幅步长为0.1 g，步长增量取0.02 g，则调幅系数λ=0.469。具体调幅过程见表3。本文在计算地震弹塑性时程反应时，采用经典的Rayleigh阻尼，结构的阻尼比取为5%。

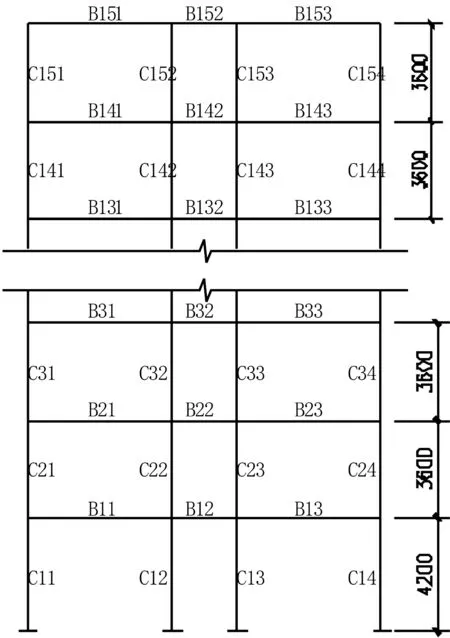
图2 单元编号

经过调幅进行了15次弹塑性动力时程分析，得到16个点，运用三阶样条插值，近似得到完整的IDA曲线，如图3所示。

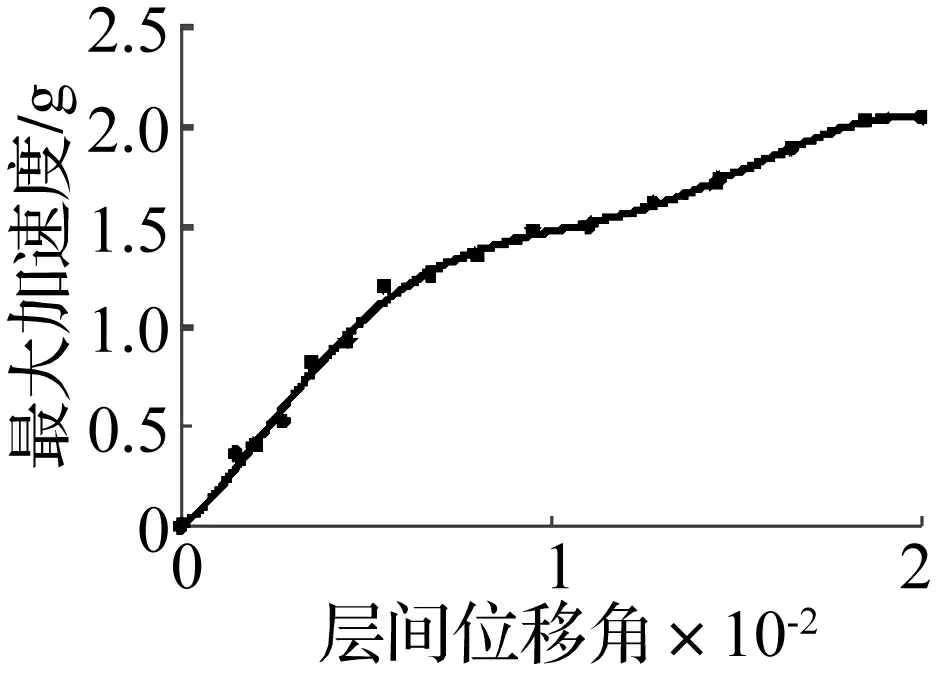
图3 Kobe地震波的IDA曲线

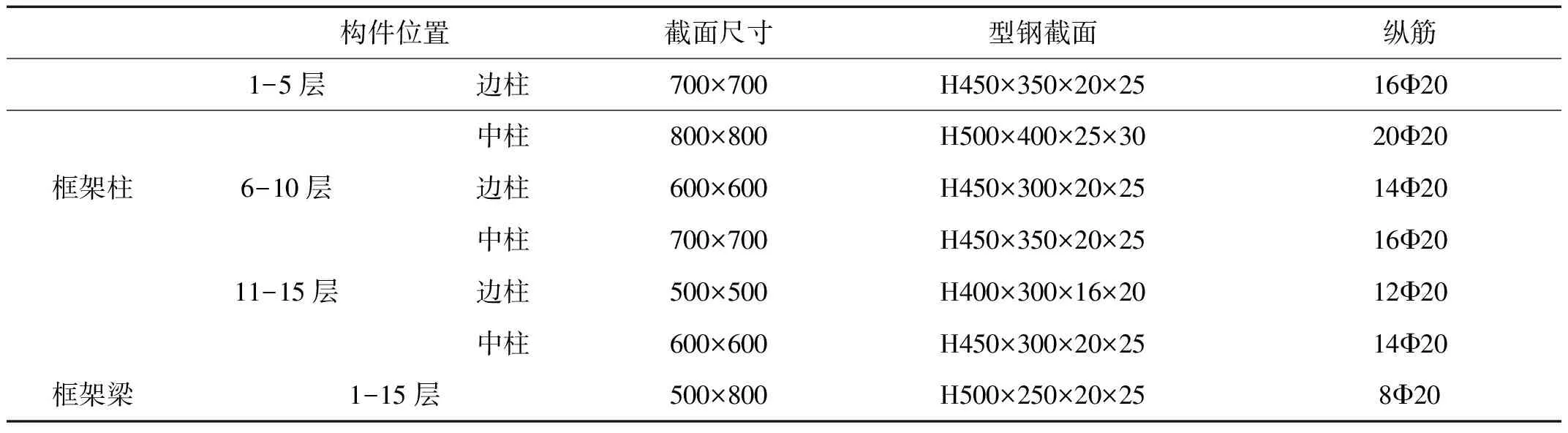
表1 结构尺寸及配筋

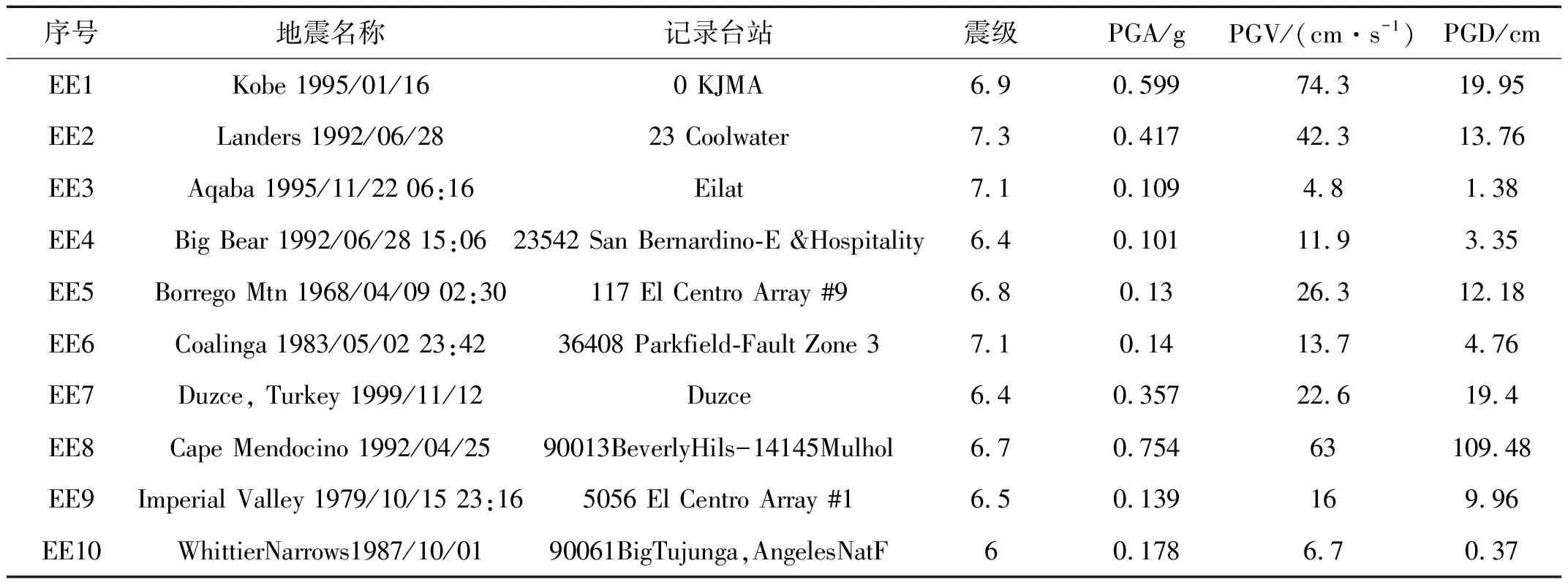
表2 地震动输入参数

表3 EE1地震记录调幅

5 基于IDA方法失效模式的识别

采用所选的十条地震波对型钢混凝土框架结构计算模型进行增量动力弹塑性分析，把每次IDA分析得到的结果在二维坐标系中表示出来，用横轴表示结构的层间位移角最大值，纵轴表示峰值加速度 PGA，得到结构的IDA曲线如图4所示。可以看出，除其中EE9和EE10的曲线出现“硬化性”特征以外，其余8条IDA曲线都符合结构的抗震性能反应。

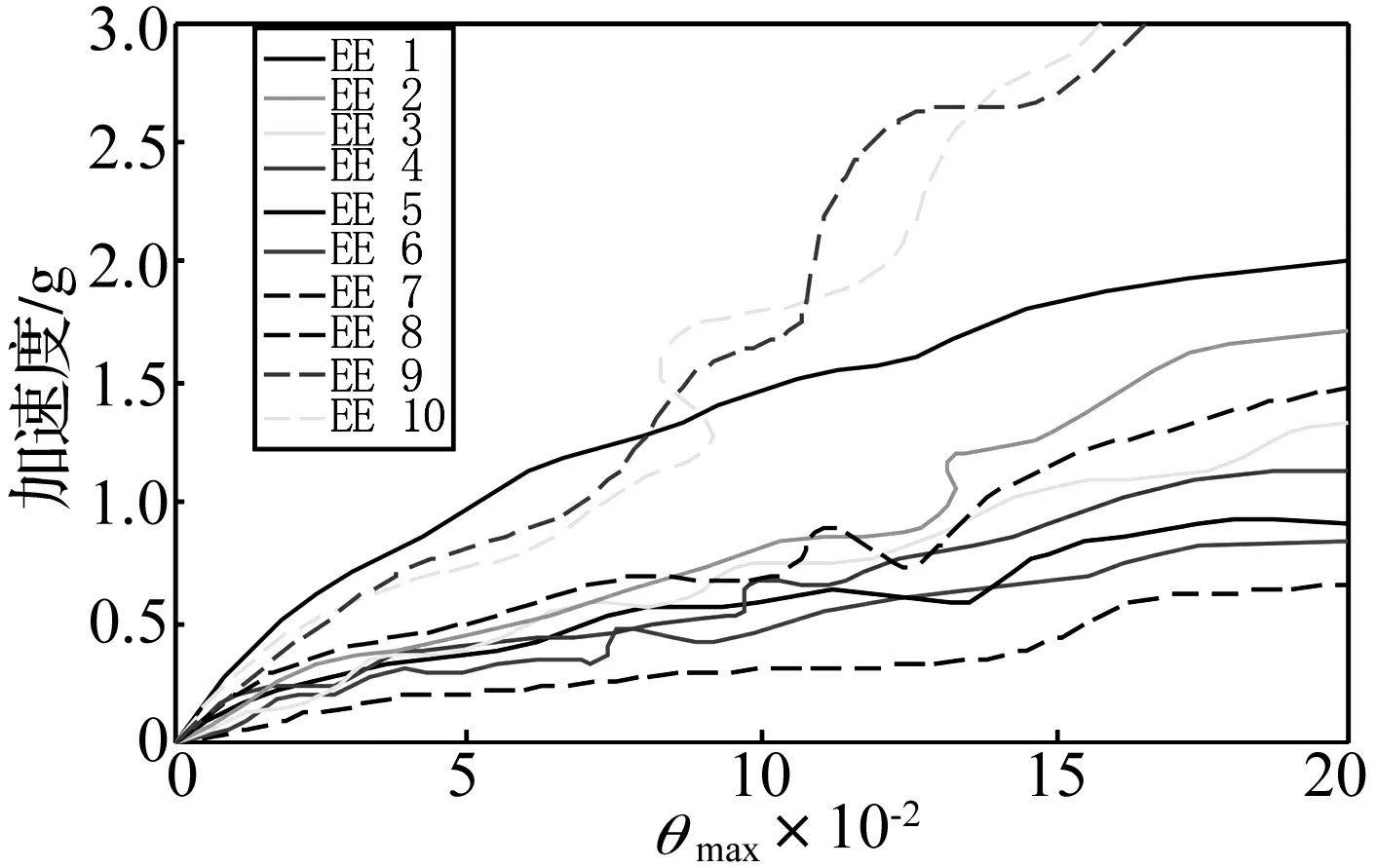
图4 结构IDA曲线

在不同地震动作用下，结构会有不同的失效模式其 PGA、最大层间位移角、最大顶点位移、最大基底剪力均不同，结构失效对比信息如表4所示。在输入的多条地震动中找出对结构影响最大的地震动，即在该地震动作用下，结构抗震性能最差，承载力最低，那么在该地震动作用下的结构失效模式认为是结构最弱失效模式。当然由于未来地震动的不确定性，选择的地震动不可能覆盖未来的所有情况，该失效模式只是一定概率水准上的结构最弱失效模式。由图4可知，输入地震动对结构的失效模式影响显著，结构在Cape Mendocino地震波作用下，当遭受强度较小的地震作用时，结构的响应最大，结构最易发生破坏,根据最弱失效原则，选取Cape Mendocino波作为结构的控制波，结构在控制波作用下的失效模式作为结构的“最弱失效模式”。

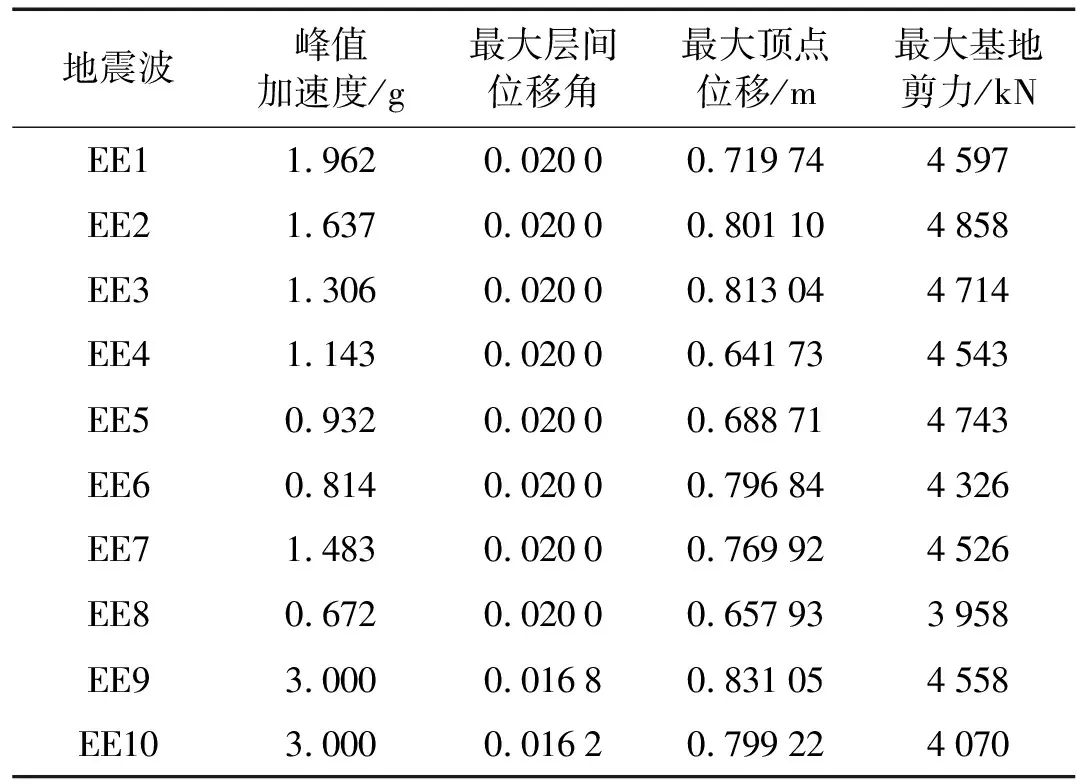
表4 结构失效信息对比

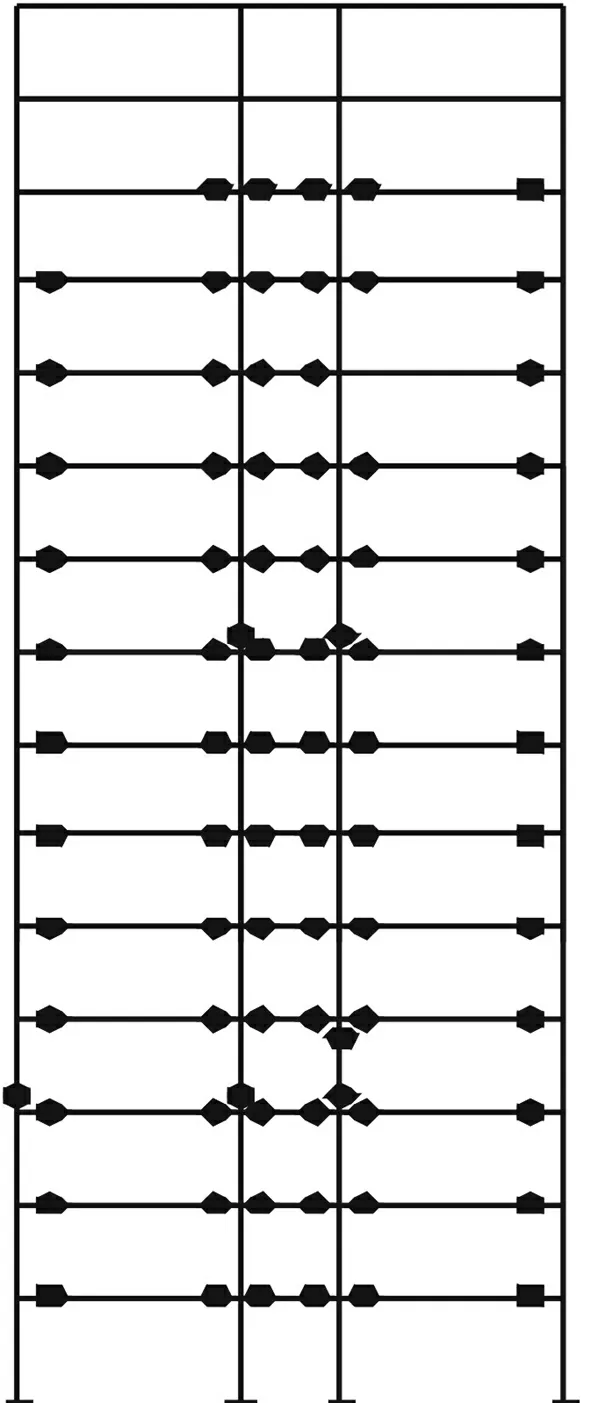
图5 结构在EE8波作用下的失效模式

本文识别结构失效模式的思路是：首先利用OpenSEES虚拟的时间序列得到IDA分析中每个分析步与相应时间点的对应关系；然后，利用Recorder模块记录关键点处型钢和混凝土的截面应力和应变。最后，利用Matlab编程工具将所有失效构件截面按先后顺序排列，这些截面的失效顺序就是该结构的一种失效模式。

分析可得不同截面的失效顺序，见表5。其中C21D(U)、B62L(R)等中的B、C代表梁和柱，B和C后面的数字代表构件，D(U)代表柱的上端截面和下端截面，L(R)代表梁的左端截面和右端截面。结构在EE8波作用下的失效模式见图5。

6 结构最弱失效模式的优化

建筑结构不合理的失效模式将导致结构不能继续承受较大的水平地震作用和竖向荷载。借鉴延性设计的思想，如果能避免结构破坏集中在某一部位或某一层，使结构的所有构件以及所有层都具有相同的抗震性能，这样结构的抗震能力将有较大的提升。本文根据表5的失效路径和图5所示的结构失效模式，以及国内外先进的优化方法[10～12]，提出了结构的优化方案。

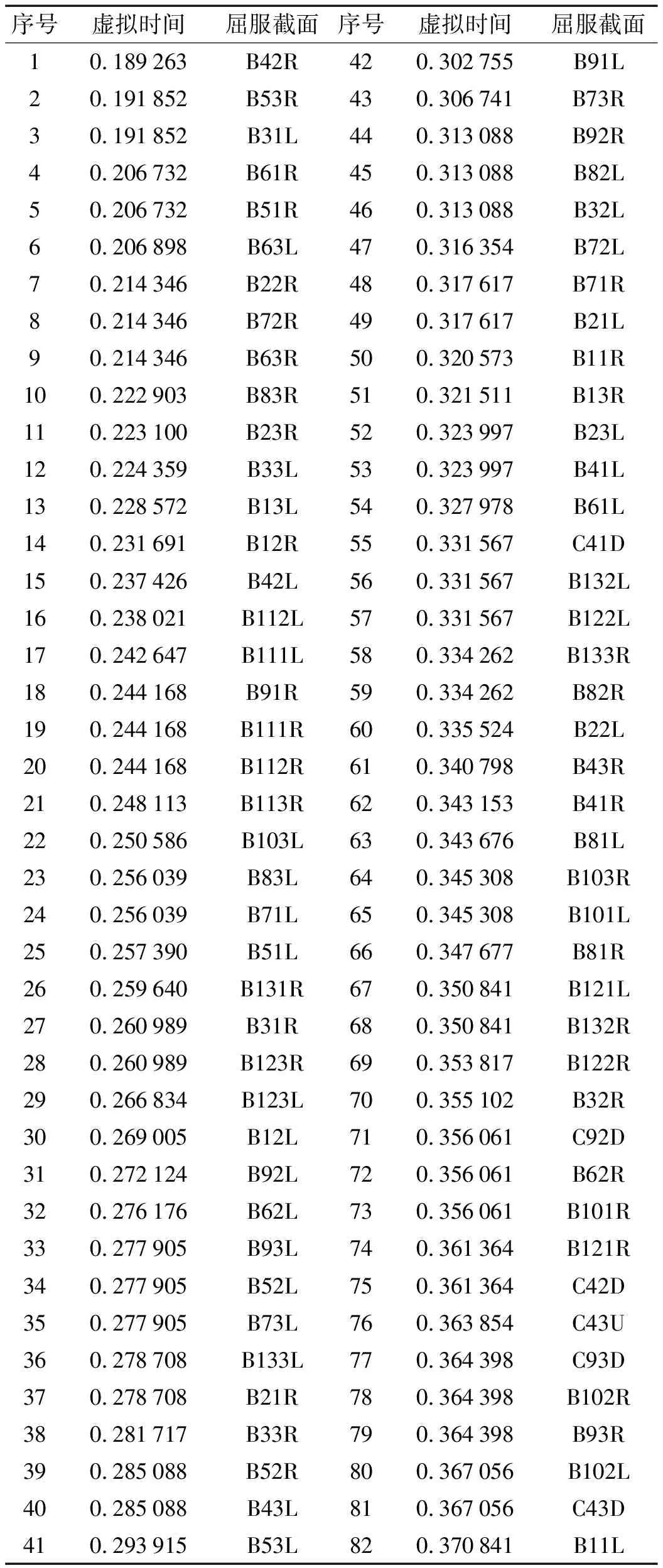
表5 构件截面屈服顺序

由表5可以看出，结构破坏以梁铰破坏为主，柱构件出现失效的截面个数较少，第四层的柱截面失效导致结构形成薄弱层。由图5可以看出，结构在第四层失效破坏比较集中。采用根据失效路径加固失效截面和依次加强薄弱层的方法来优化结构的失效模式。结合对结构失效模式的搜索，提出结构失效模式的几种优化方案：

优化方案一：根据失效路径可以看出结构第四、五、六层首先出现梁铰破坏，故可采用加大第四、五、六层梁的配钢率方案，将梁中型钢截面由H500×250×20×25增大为H600×300×25×30。

优化方案二：逐步消除薄弱层的方法。在结构形成机构前，第四层首先由于层间位移角过大导致结构失效，该层即为薄弱层，因此加强第四层的梁和柱，梁中型钢截面由H500×250×20×25增大为H600×300×25×30，边柱型钢截面由H450×350×20×25增大为H550×450×25×30，中柱型钢截面由H500×400×25×30增大为H600×450×25×30。加强第四层后结构刚度矩阵会随之改变，形成一个或者多个新的薄弱层，按照从下向上的顺序依次加固薄弱层，使结构的各层趋于同时失效以提高结构的抗震性能。

优化方案三：结合方案(一)和方案(二)，加强第四、五、六层梁和第四层的柱。

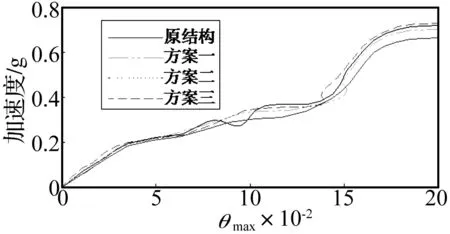
图6 优化前后结构的IDA对比曲线

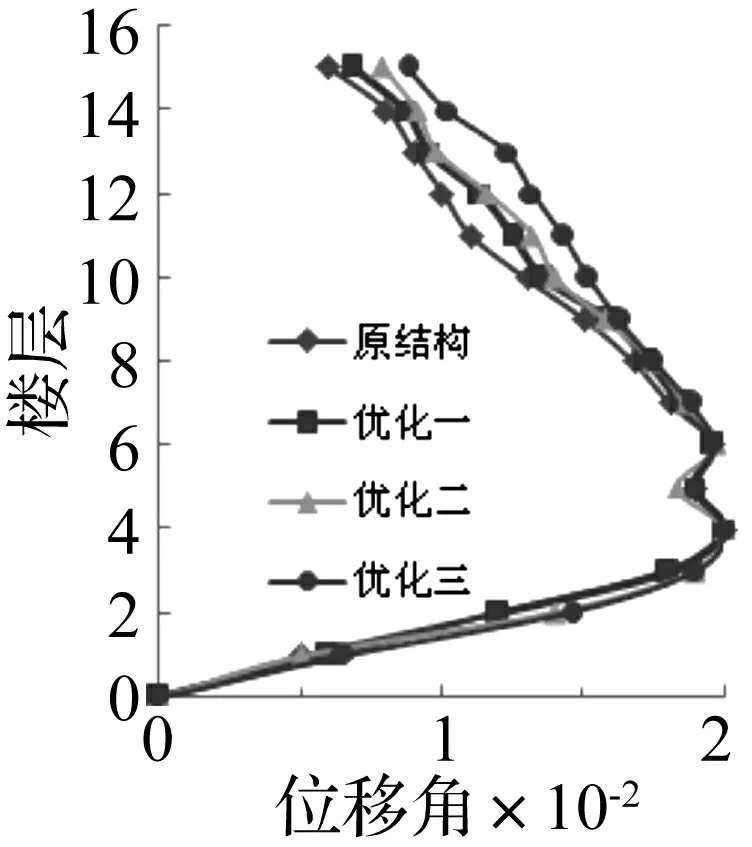
图7 结构层间位移角对比

采用控制波Cape Mendocino波对三种改善方案后的结构进行IDA分析得到与原结构的IDA对比曲线，见图6。为了更好地了解优化后结构抗震性能的变化，这里给出能代表结构抗震性能不同指标的对比曲线，图7为结构层间位移角对比图，表6为结构优化前后失效信息对比。

从以上优化后结构与原结构抗震性能指标的对比可以看出，方案一根据失效路径加强地震失效模式可能会导致结构的延性降低，方案二和三对结构延性改变不大，采取三种方案优化后，结构的PGA增大，从而能够承担更大的基底剪力。从图7看出，优化后各层层间位移角增大并趋于一致，表明各层损伤趋于均匀，结构耗散地震能量的能力更强，且方案三的效果优于方案一和方案二。

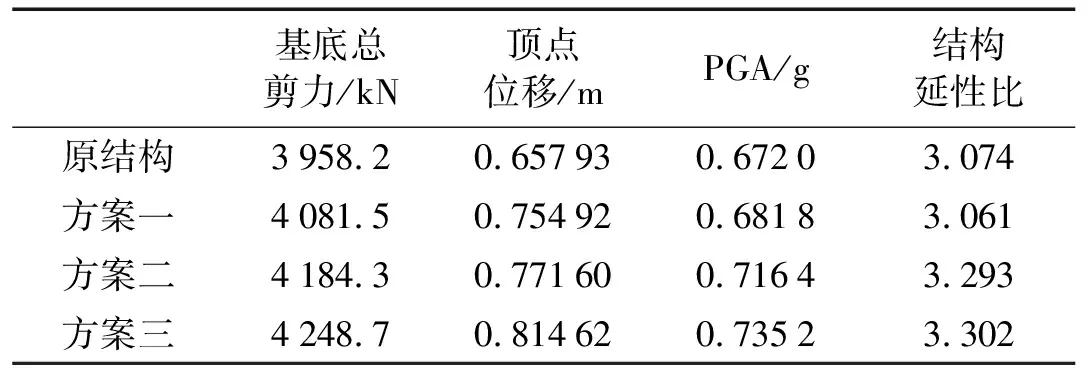
表6 结构优化前后失效信息对比

7 结 论

本文基于OpenSEES平台对型钢混凝土结构进行多次IDA分析，搜索出影响结构抗震性能的控制地震波，进而获得该地震波作用下结构的失效模式，并采取一些工程设计方法对其进行优化设计。得到以下结论：

(1)通过IDA分析方法对型钢混凝土框架结构进行分析，较好地获得了结构在不同地震强度下的性能反应，提出了比较合理的失效模式识别方法，并对“最弱失效模式”进行了有效阐述。

(2)采用概念优化的方法，根据加固失效路径加固失效截面并加强薄弱层，能较好地改善结构的抗震性能。其中，方案一可提高结构抗震承载力，但会相应地降低结构的延性；方案一和方案二结合后，结构承载力和延性均有明显改善。表明采用基于IDA方法及相关工具搜索既有结构的失效模式并进行工程优化的途径合理可行。

(3)由本文得到的IDA曲线可知，输入地震波的选取对结构IDA分析结果影响较大，不同输入地震波得到的结构失效模式也有一定的差异，所以如何选取适合计算模型的地震波以便能得到准确的结构最弱失效模式，还有待更深入的研究。

参 考 文 献

[1]孙景江，马 强，石宏斌,等.汶川地震高烈度区城镇房屋震害简介[J].地震工程与工程振动，2008，28(3)：7-15.

SUN Jing-jiang,MA Qiang,SHI Hong-bin,et al.Building damage in cities and towns located in higher intensity areas during Wenchuan earthquake [J].Journal of Earthquake Engineering and Engineering Vibration,2008,28(3):7-15.

[2]孙 海，梁立孚，侯钢领.结构最弱失效模式组的优化及投资-效益模型[J].哈尔滨工程大学学报，2009，30(3): 262-266.

SUN Hai,LIANG Li-fu,HOU Gang-ling.Optimization and investment-benefit model of the weakest failure modes of structural systems [J].Journal of Harbin Engineering University,2009,30(3): 262-266.

[3]欧进萍，段宇博.高层建筑结构的抗震可靠度分析与优化设计[J].地震工程与工程振动，1995，15(1): 1-13.

OU Jin-ping,DUAN Yu-bo.Seismic reliability analysis and optimum design of tall buildings[J].Journal of Earthquake Engineering and Engineering Vibration,1995,15(1): 1-13.

[4]孙爱伏，欧进萍.高层钢结构地震失效模式控制的失效路径修正法[J].地震工程与工程振动，2010，30(1): 22-28.

SUN Ai-fu,OU Jin-ping.Seismic failure mode control of tall steel buildings by changing the failure path [J].Journal of Earthquake Engineering and Engineering Vibration,2010,30(1): 22-28.

[5]白久林，欧进萍.基于 IDA 方法的钢筋混凝土结构失效模式优化[J].工程力学，2011，28(增刊2): 198-203.

BAI Jiu-lin,OU Jin-ping.Optimization of failure modes for reinforced concrete buildings based on IDA method[J].Engineering Mechanics,2011,28(sup2): 198-203.

[6]吴巧云,朱宏平,樊 剑,等.某框架结构的抗震性能评估[J].振动与冲击，2012，31(15): 158-164.

WU Qiao-yun,ZHU Hong-ping,FAN Jian,et al.Seismic performance assessment on some frame structure[J].Journal of Vibration and Shock,2012,31(15):158-164.

[7]刘海卿，倪镇国，张 颖.多层框架结构地震倒塌过程仿真分析[J].科学技术与工程，2009,9(2):472-475.

LIU Hai-qing,NI Zhen-guo,ZHANG Ying.Simulation analysis for the collapse response of frame structures under macroseism[J].Science technology and engineering,2009,9(2): 472-475.

[8]杨 溥，李英民，赖 聪.结构时程分析法输入地震波的选择控制指标[J].土木工程学报，2000，33(6):33-37.

YANG Pu,LI Ying-min,LAI Cong.A new method for selecting inputing waves for time-history analysis [J].China Civil Engineering Journal,2000,33(6): 33-37.

[9]玉 军.钢筋混凝土高层建筑结构抗震弹塑性分析方法的研究及其应用[D]．长沙：湖南大学，2007.

[10]Charles V.Camp,Shahram Pezeshk,Hansson H.Flexural design of reinforced concrete frames using a genetic algorithm[J]． Journal of Structural Engineering,2003,129(1): 105-115.

[11]Lee C,Ahn J.Flexural design of reinforced concrete frames by genetic algorithm[J].Journal of Structural Engineering,2003,129(6): 762-774.

[12]Pezeshk Bys,Camp C V,Chen D.Design of nonlinear framed structures using genetic optimization[J].Journal of Structural Engineering,2000,126(3): 382-388.