铣削颤振稳定域叶瓣图确定方法研究

迟玉伦， 李郝林

(上海理工大学 机械工程学院 上海 200093)

随着高速数控机床向高加工精度、高生产效率的发展，伴随切削加工一个严重问题就是颤振。颤振是发生在切削过程中一种强烈的自激振动，颤振会严重制约切削效率、降低零件的加工精度、损坏刀具甚至是机床。目前，很多学者对颤振现象进行了大量工作[1-7]。避免颤振发生最有效方法是使用颤振稳定性叶瓣图，稳定性叶瓣图是把切削稳定区、非稳定区表示成轴向切削深度与主轴转速之间的函数[2]。Altinas等[1]提出的颤振稳定域求解方法已经得到了实验验证[3]。由于铣削过程的复杂性以及各参数测量计算方法等原因，无法准确确定刀具刚度、径向切削力系数、切向切削力系数等常数参数，致使铣削颤振稳定域叶瓣图难以准确确定。Quintana等[6-7]提出了通过切削倾斜工件表面的实验设计方法来有效确定颤振稳定域叶瓣图。但该实验设计方法往往需要上百次切削实验才能完整确定出颤振稳定域叶瓣图，在实际加工中难以得到应用。

基于上述研究，本文提出了通过理论模型计算与实验设计相结合方法确定铣削颤振稳定域叶瓣图。在建立铣削颤振稳定域数学模型基础上，选取4～7个主轴转速对斜表面工件进行切削实验，实验过程中利用声发射信号分别识别出对应于各主轴转速的临界切削深度。运用锤击法获得振动系统固有频率和阻尼比。基于实验测量数据和理论模型计算，利用遗传算法来优化确定各常数参数，从而绘制出与实验测量结果相一致的铣削颤振稳定域叶瓣图。该叶瓣图可有效应用到该机床实际铣削加工过程中的参数选择，对提高铣削加工效率和加工质量有重要意义。

1 铣削颤振稳定性叶瓣图数学模型

如图1所示，铣削系统可简化为X、Y两个方向上的二自由度振动系统[8-9]，以用矩阵形式表示的动态铣削力为：

(1)

式中，Ktc为径向切削力系数，ap为轴向切削深度，{Δ(t)}为动态位移向量，[A0]为平均方向性系数矩阵。

图1 铣削系统动力学模型

由于[A0]只有在刀具切入角φst与切出角φex之间时才有效，即g(φj)=1，故上式可表示为：

(2)

式中，平均方向系数可表示为：

(3)

式中，Kr为径向切削力系数Krc与切向切削力系数Ktc之比。

考虑到再生效果的动态铣削力可表示为：

(4)

式中，ωc为颤振频率，[Φ(iωc)]为刀具与工件频响函数之和，如下式：

(5)

式(4)有非奇异解的条件为：

det{[I]-Λ[Φ0(iωc)]}=0

(6)

式中，[I]为单位矩阵，[Φ0(iω0)]为有向传递函数矩阵。

该特征方程的特征值，可表示为：

(7)

式中，N为刀齿数，忽视交叉传函Φxy和Φyx，可以得到特征值Λ为：

(8)

式中：

a0=Φxx(iωc)Φyy(iωc)(axxayy-axyayx)

a1=axxΦxx(iωc)+ayyΦyy(iωc)

(9)

因为传递函数为复数，故其特征值包含实部和虚部，而轴向切深为实数，将Λ=ΛR+iΛI及e-ωcT=cos(ωcT)-isin(ωcT)代入式(7)，并令虚数部分必为零，得：

(10)

结合上述式(7)和式(9)，可以得到临界轴向切削深度的最终表达式为：

(11)

主轴转速可以通过求得刀齿切削周期T得到：

(12)

式中，k为叶瓣数，k=0,1,2…。

综上所述，对于给定的刀具、根据刀具系统的固有频率ωn、阻尼比ζ、刀具刚度K、径向切削力系数Krc、切向切削力系数Ktc及颤振频率，利用式(8)可计算出特征值的实部和虚部，进而利用式(10)～(12)计算出轴向临界切深aplim及相应的主轴速度n，针对所选叶瓣数和颤振频率范围重复上述过程，可获得颤振稳定域分析解。

运用锤击法对机床的刀具系统进行锤击试验，可获得固有频率ωn和振动系统的阻尼系数ζ。由于铣削过程的复杂性以及各参数测量计算方法等原因，无法准确确定刀具刚度K、径向切削力系数Krc、切向切削力系数Ktc等常数参数，致使铣削颤振稳定域叶瓣图不能准确确定。本文通过理论模型计算与实验设计相结合方法来确定参数K、Krc、Ktc的值。

2 实验研究

2.1 实验

如下图2所示，本实验机床为VMC850E三轴立式加工中心,被加工工件材料为45钢，切削刀具为Φ10 mm双刃平底刀，刀具伸长长度为58 mm。实验加工过程中，通过声发射信号对铣削颤振现象进行辨别，该实验利用SBS声发射传感器AE1000对切削加工过程进行监测，其声发射信号通过高速数据采集卡Spectrum M1.3120(2通道，12位A/D转换)传输到计算机，采样频率设置为1 MHz。

图2 铣削实验装置

如图3所示，该实验的工件形状长为100 mm、高为5 mm。设置机床不同加工参数，如下表1所示，每齿进给量f为0.06 mm，本实验选用5个不同主轴转速对工件材料进行单边逆铣切削，在切削过程中，刀具的切削深度是从一开始0 mm逐渐增大到5 mm。

表1 铣削加工工艺参数表

图3 切削工件材料形状图

根据Dornfeld等[10-11]研究沿倾斜工件表面铣削加工时，随着切削深度增大，系统会由强迫振动转变成自激振动，铣削过程发生颤振而不稳定。如下图4(a)所示，当机床转速为S1=2 389 r/min时，利用声发射信号监测铣削过程中发生颤振时的临界切削深度，其中B点为强迫振动和自激振动的转化点，即为发生颤振时的临界切削深度amax1=2.18 mm，如下图4(b)所示，与声发射监测信号相对应的切削工件表面质量情况，证明了该方法监测铣削过程颤振的有效性和实用性。

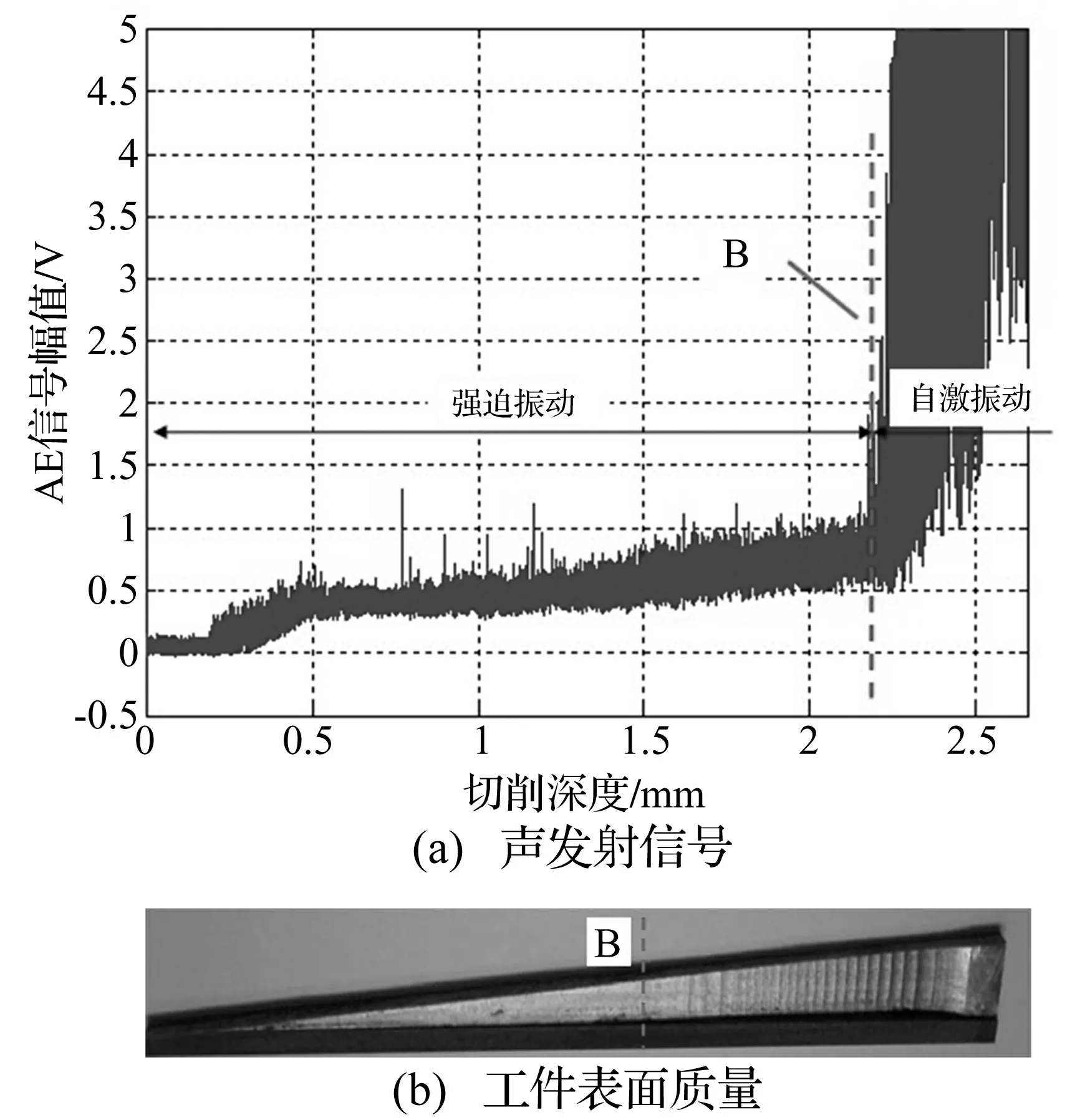
图4 基于声发射信号的铣削颤振识别

基于上述声发射信号识别铣削颤振方法，分别对其他主轴转速S2=3 344 r/min、S3=4 299 r/min、S4=5 255 r/min和S5=6 210 r/min进行切削实验，获得各主轴转速下发生颤振时的临界切削深度amax2=2.80 mm，amax3=1.91mm，amax4=1.55mm，amax5=4.55mm，如下表2所示。

表2 实验测量各主轴转速对应临界切削深度

最后，运用锤击法对机床的刀具系统进行锤击试验，将加速度计安装在主轴末端刀尖部位，用力锤在另一侧敲击，被测加速度和力信号经放大后被采集到计算机，经处理后可获得振动系统固有频率ωn=453 Hz和阻尼比ζ=0.036 3。

2.2 铣削颤振稳定域叶瓣图的确定

由上述实验可获得系统的固有频率ωn=453 Hz和阻尼比ζ=0.036 3。为准确确定刀具刚度K、径向切削力系数Krc、切向切削力系数Ktc等常数参数，本文利用遗传算法对此常数参数优化，设K、Krc、Ktc的约束条件为Kmin≤K≤Kmax，Krcmin≤Krc≤Krcmax，Ktcmin≤Ktc≤Ktcmax，对应于任一组参数{K,Krc,Ktc}，可计算出铣削颤振稳定域叶瓣图在各主轴转速S1～S5的理论临界切削深度h1～h5，基于上述表2实验测量各主轴转速S1～S5的实验临界切削深度amax1～amax5，设目标优化函数Pmin：

(13)

式中，m为实验次数，本实验m=5，hi为理论计算的临界切削深度，amax1为实验测量的临界切削深度。

正规化后，常数参数作为个体的表现形式为：

(14)

选定遗传算法的参数，世代数为30，个体数100，一个变量个体的位长l=9，交叉率为0.6，突然变异率为0.001。其优化结果K=1.1×107N/m，Krc=810 N/mm2，Ktc=176 N/mm2,Pmin=0.05。

图5 铣削颤振稳定域叶瓣图

利用上述确定的各常数参数绘制出的铣削颤振稳定域叶瓣图，如图5所示，理论计算的颤振稳定域叶瓣图与实验测量结果相一致。理论上实验测量点数m越大，理论计算的叶瓣图越准确，考虑到快速方便建立该叶瓣图，通常选择实验测量点数m=4～8。

2.3 实例应用

将上述方法应用到某机床生产企业的BVMC1370三轴立式加工中心,被加工工件材料为45钢，切削刀具为Φ12 mm双刃平底刀，刀具伸长长度为60 mm，其主轴转速最高为10 000 r/min，最大切削进给速度为12 000 r/min。

根据上述理论方法对单边逆铣切削过程的工艺参数进行优化选取，并与原有经验参数对比如表3所示。显然根据该理论分析方法选取的切削加工参数更加合理，加工效率也更高，切削加工结果验证了该方法的有效性和实用性。

表3 BVMC1370加工中心优化前、后参数对照表

考虑到实际切削过程中，如工件材料，刀具型号以及机床结构等各种因素的影响，需对不同机床加工条件状况下进行实验测量与理论分析建模(机床-刀具系统可简化为单自由度系统)，可根据上述方法绘制出各自的颤振稳定域叶瓣图后进行加工参数优化选取。

通常机床-刀具系统为多自由度系统，反映到机床-刀具接触区频响函数(简称FRF)的图形具有多峰[3]，可将每个峰作为单自由度进行处理，依据上述实验原理方法依次构造出每个模态所对应的稳定性叶瓣图，保留每个转速下的最小临界切削深度对图形进行修剪，可得到多自由系统的稳定性叶瓣图。

3 结 论

(1)对于经典颤振稳定域数学模型，有些常数参数难以准确确定，本文提出了基于实验设计的确定颤振稳定域叶瓣图的方法。

(2)设计了基于声发射信号识别铣削颤振的实验方案，选取多个主轴转速对斜表面工件进行切削实验，利用声发射信号分别识别出对应于各主轴转速的临界切削深度。运用锤击法获得振动系统固有频率和阻尼比。

(3)基于实验测量数据和理论模型计算相结合方法，建立约束条件和目标函数，利用遗传算法来优化确定各常数参数，从而绘制出与实验测量结果相一致的铣削颤振稳定域叶瓣图。

(4)最后，本文将该方法应用到某机床生产企业的BVMC1370三轴立式加工中心的实际加工过程中的切削参数优化选取，取得了较好的实验结果。后续文章将对该方法在机床-刀具多自由度系统中的应用进行更多研究。

参 考 文 献

[1]Altintas Y,Stepan G,Merdol D,et al.Chatter stability of milling in frequency and discrete time domain[J].CIRP Journal of Manufacturing Science and Technology,2008,1:35-44.

[2]李忠群，刘 强.基于频响函数的高速铣削颤振稳定域快速分析与研究[J].制造技术与机床，2008(4):53-61.

LI Zhong-qun,LIU Qiang.Rapid analysis on chatter stability lobes for high speed milling based on frequency response function[J].Manufacturing Technology & Machine Tool,2008:53-61.

[3]Li Z Q,Liu Q.Solution and analysis of chatter stability for end milling in the time-domain[J].Chinese Journal of Aeronautics 21(2008)：169-178.

[4]Tang W X,Song Q H,Yu S Q,e tal.Prediction of chatter stability in high-speed finishing end milling considering multi-mode dynamics[J].Journal of Materials Processing Technology,2009,209:2585-2591.

[5]刘安民，鹏 程,刘吉兆，等.高速铣削时颤振的诊断和稳定加工区域的预报[J].机械工程学报，2007(1):164-169.

LIU An-min,PENG Cheng,LIU Ji-zhao,et al.Detection of chatter and prediction of stable cutting zones in high-speed milling[J].Chinese Journal of Mechanical Engineering,2007(1):164-169.

[6]Quintana G,Ciurana J,Ferrer I,et al.Sound mapping for identification of stability lobe diagrams in milling processes[J].International Journal of Machine Tools & Manufacture,2009,49:203-211.

[7]Quintana G,Ciurana J,Teixidor D.A new experimental methodology for identification of stability lobes diagram in milling operations[J].International Journal of Machine Tools &Manufacture,2008,48:1637-1645.

[8]刘 强，李忠群.数控铣削加工过程仿真与优化[M].北京：航空工业出版社,2011,7.

[9]Wan M,Zhang W H,Dang J W,et al.A unified stability prediction method for milling process with multiple delays[J].International Journal of Machine Tools & Manufacture,2010,50:29-41.

[10]Dornfeld D.Precision Manufacturing,first ed.,[M].Springer,New York,NY,2007.

[11]Ding Y,Zhu L M,Zhang X J,et al.A full-discretization method for prediction of milling stability[J].International Journal of Machine Tools & Manufacture,2010,50:502-509.