厚层底水油藏油井临界产量计算方法

涂 彬， 韩 洁, 孙 键

(1.石油工程教育部重点实验室(中国石油大学(北京))，北京 102249；2.中国石油勘探开发研究院，北京 100083；3.中国石化石油工程技术研究院，北京 100101)

底水锥进现象发生在倾角很小，油水接触面积很大的平缓地层中[1]。底水锥进的状况比较复杂，特别是水锥的形状不能用一般数学方法来描述，截至目前，还没有关于水锥问题的精确解。为了避免出现水锥现象，需要将油井产量控制在临界产量以下。目前，针对底水油藏临界产量的研究较多[1-5]，总体来看，这些研究都做了一些近似。其中一种方式是将流体在地层中的渗流近似为平面径向流[1-3]，这种近似对于比较薄的底水油藏具有较高的准确性，但对于较厚的底水油藏(如辽河油田潜山裂缝性油藏，厚度在100～300 m，甚至更厚)，则可能产生误差。Boyun Guo[3]等人在考虑直井射孔段比较长的情况下，把地下的流动分为平面径向流(射孔井段所在地层)和半球面流(井底以下部分)，根据这一假设推导出了临界产量计算公式；和Dupuit底水油藏临界产量公式相比，该公式考虑了射孔段长度对临界产量的影响，并可以根据该公式优化射孔段长度。Schols[4]在Hele-Shaw模型(平行流动)基础上通过试验，归纳出了临界产量的经验计算公式，但该公式没有考虑垂向渗透率的影响。侯君等人[5]认为在油层打开程度小于2/3时，地层内流体渗流应该采用球形向心流模型。

针对目前底水油藏临界产量研究中存在的问题，笔者根据厚层油藏球形向心流和平面径向流理论和稳定渗流理论，综合考虑油层厚度、射孔厚度、油水重度以及油层水平、垂向渗透率等因素，在厚层底水油藏水锥物理模型的基础上，推导出适用于厚层底水油藏的临界产量计算公式，从而为厚层底水油藏制定合理的产量提供依据。

1 厚层底水油藏水锥物理模型

一个充满单相流体的地层，储层厚度为h，油藏供给半径为Re，油井半径为rw，地层渗透率为K，供给压力和井底压力分别为pe和pw，原油和水的黏度分别为μo和μw，其密度分别为ρo和ρw。地层厚度足够大时，可以将其中的渗流看成是由2部分构成(见图1(a))：第1部分是液流从较远的地方(假设供给半径为Re)到距井中心线为Rr的平面径向流(此时流动在整个地层，可以忽略流体重力)；第2部分是自Rr处开始向井的球形向心流[6]。从电解模型试验得到证实，在Rr>1.5h之后,球形流很快退化为平面径向流，此时该渗流模式下的产量计算公式为[6]：

(1)

图1 厚层底水油藏渗流模型Fig.1 Seepage model for thick reservoir with bottom water

厚层底水油藏水锥如图1(b)所示，地层上部ho厚度被石油充满，水占据地层下部，油井射孔厚度为hp，未投产前，油层处于静止状态，油水界面原始位置CC。当油井以某产量投产时，由于流体上升速度的影响，油水界面变形并上升到CDC。在油井产量一定的情况下，油水界面可能稳定在CDC位置不动。此时，厚层油藏油层内流体的渗流可简化分成2个区域：第1个区域为平面径向流，渗流的起点为外边界Re，势为Φe，油水界面处于原始位置，渗流的终点为距离油井中心线Rr处，势为Φr，油水界面的位置为z1；第2个区域为球形向心流，渗流的起点为距离井中心线半径Rr处，渗流的终点近似为射孔井段的中心，如图1(b)所示。

(2)

2 厚层底水锥起临界产量公式推导

假设条件：稳定渗流、均质地层、忽略毛管力，油水密度及黏度为常数，渗流符合达西渗流规律。

2.1 水锥区域渗流的侧面积

在径向r处取一个微元体(见图2)，当油井产量为Q时，考虑到在空间中流体的渗流是通过一个球面，因此在该点的渗流速度为：

(3)

图2 油水界面处渗流速度示意Fig.2 Schematic diagram of seepage velocity at the oil-water contact

在水锥区域，渗流的截面积是距离油井中心线r处所对应的圆台的侧面积，根据圆台的面积公式[7]，可以将渗流的截面看做是以半径r为底的两个圆台的叠加(见图3)，因此得到这2个圆台的侧面积为：

As=2πr(ho-z)

(4)

该侧面积即为以油井为中心，平面径向流在距离油井中心线r处的渗流截面积。

2.2 平面径向流区域临界产量公式

根据地层中平面径向流渗流速度与势函数的关系，可以知道当渗流为平面径向流时，通过地层距离油井中心线r处的流量为[8]：

图3 渗流截面示意Fig.3 Schematic diagram of seepage section

(5)

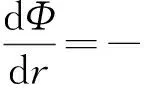
πΔρwogKh(ho-z)dz

(6)

当油井产量达到临界产量时，在径向流区域内：Q=Qoc；r=Re处，Φ=Φe，对应高度z=0；在r=Rr处，Φ=Φr，对应高度z=z1。此时对式(6)两边进行积分得：

πΔρwogKh(ho-z)dz

(7)

2.3 球形向心流区域临界产量公式

根据球形向心流的渗流速度与势函数的关系，可以知道距离油井中心线r处的流量为：

(8)

考虑张量理论[9]以及流体势与高度的关系，对式(8)分离变量得：

(9)

(10)

2.4 厚层底水油藏水锥临界产量公式

结合式(7)和式(10)可得:

(11)

Rr为球形向心流和平面径向流的交接处，根据文献[6]，可令Rr=1.5ho，代入式(11),整理得临界产量公式为：

(12)

3 实例验证

辽河油田某厚层底水油藏的一口采油井，油层厚度33.80 m，射开厚度10.00 m，油层平均渗透率0.356 D，其他相关参数为：ρw=1.086 g/cm3，ρo=0.648 g/cm3，ρos=0.857 g/cm3，μo=1.0 mPa·s，Re=450.00 m，rw=0.10 m，Bo=1.33，把以上参数代入Dupuit公式计算得到的临界产量为33 t/d，代式(12)计算得到的临界产量为43 t/d。该井产量在较长期间内保持40 t/d的水平，已生产3年，累计产油量达到2.6×104t，未见水，说明对于厚层底水油藏，式(12)比Dupuit公式具有更好的适用性。

4 敏感因素分析

假设某油藏的相关参数为：hp=8.00 m，Kv=Kh=0.4 D，ρw=1.10 g/cm3，ρo=0.70 g/cm3，ρos=0.83 g/cm3，μo=0.5 mPa·s，Re=500 m，rw=0.1 m，Bo=1.5[2]。将以上参数代入式(12)和Dupuit公式计算油层厚度对临界产量的影响，结果见图4。

图4 临界产量与油层厚度的关系Fig.4 Relationship between critical production and reservoir thickness

从图4可以看出：随着油层厚度的增大，临界产量增加；在其他条件一致的情况下，随着油层厚度的增加，式(12)计算的临界产量与Dupuit公式计算结果的差值增大。这表明油层厚度越大，近井区渗流的影响越大，因此当油层厚度较大时应该考虑采用式(12)计算临界产量。

利用式(12)分析了垂向渗透率与射孔厚度对临界产量的影响，结果见图5和图6。

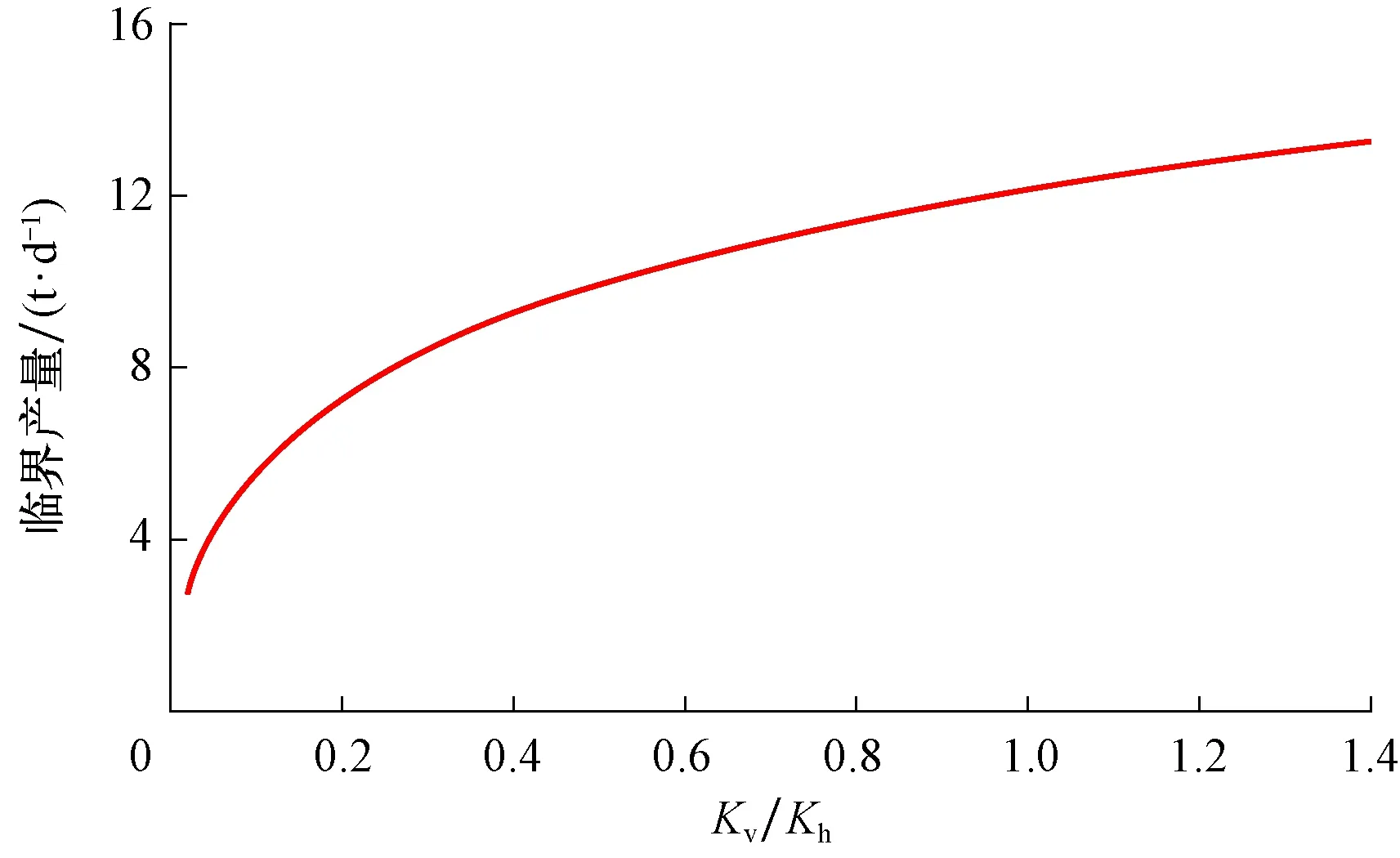
图5 临界产量与垂向渗透率的关系Fig.5 Relationship between critical production and vertical permeability

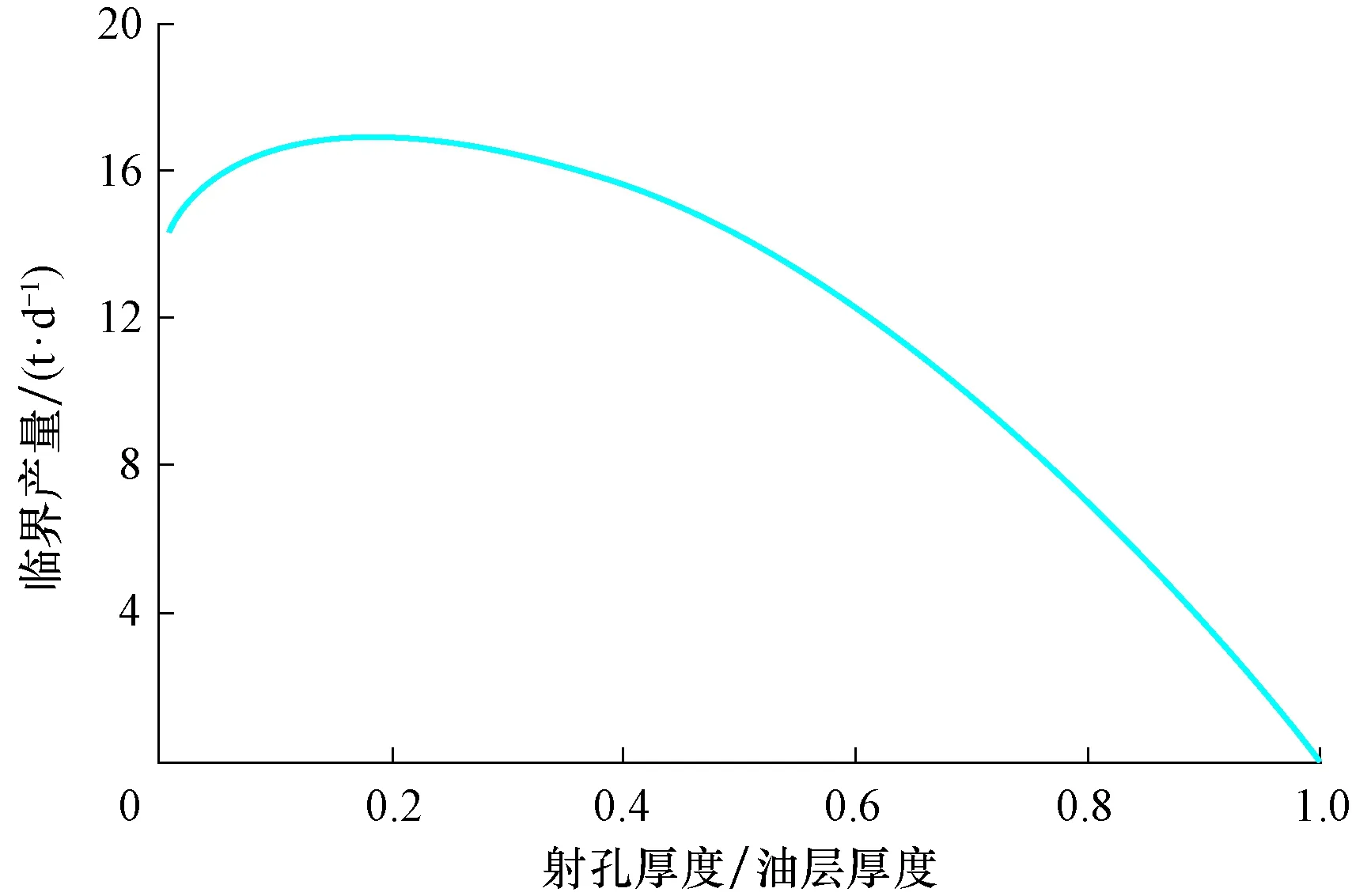
图6 临界产量与无因次射孔厚度的关系Fig.6 Relationship between critical production and dimensionless perforation thickness

从图5可以看出，随着垂向渗透率增大，临界产量增大，表明近井区的空间渗流阻力减小。从图6可以看出，临界产量随着射孔厚度的增厚先增大后减小，在射孔厚度为0.2倍油层厚度时达到最大，这表明底水油藏较优的射孔位置应在0.2倍油层厚度处；射孔位置越靠近油层底部，底水越容易锥进进入油井，造成产量损失。

5 结 论

1) 推导出的厚层底水油藏临界产量公式考虑了流体在厚层油藏中的垂向流动，更加符合厚层底水油藏的渗流特点。

2) 与Dupuit临界产量公式相比，推导出的临界产量公式考虑的因素相对更全面，更适用于油层厚度较大的底水油藏。

3) 推导出的临界产量公式是基于稳定渗流理论推导的，然而在实际生产中产量与压力是不稳定的。因此,应考虑动态要素的影响，推导以不稳定渗流理论为基础的厚层底水油藏的临界产量公式。

符号说明

参考文献
References

[1] Hagoort J.Fundamentals of gas reservoir Engineering [M].New York:Elsevier Scientific Publishing Company,1988:423-425.

[2] 李传亮．修正Dupuit临界产量公式[J]．石油勘探与开发，1993，20(4)：91-95．

Li Chuanliang.A modified Dupuit formula for critical production rate[J].Petroleum Exploration and Development,1993,20(4):91-95.

[3] Guo Boyun,Lee R L-H.A simple approach to optimization of completion interval in oil/water coning systems[R].SPE 23994,1993.

[4] Schols S R.An empirical formula for the critical oil production rate[J].Erdoel Erdgas,1972,88(1):6-11.

[5] 侯君，程林松．常规底水油藏水锥高度计算方法研究[J]．西安石油大学学报:自然科学版，2006，21(3)：23-26,114．

Hou Jun,Cheng Linsong.Calculation method for the water cone height of bottom-water reservoir[J].Journal of Xi’an Shiyou University:Natural Science Edition,2006,21(3):23-26,114.

[6] 葛家理．油气层渗流力学[M]．北京：石油工业出版社，1982．

Ge Jiali.The seepage mechanics of oil & gas in reservoir[M].Beijing:Petroleum Industry Press,1982.

[7] 数学手册编写组．数学手册[M]．北京：高等教育出版社，2005：82-83．

Writing Group of Mathematics Handbook.Mathematics handbook[M].Beijing:Higher Education Press,2005:82-83.

[8] 易俊．推导Dupuit临界产量的新方法[J]．重庆石油高等专科学校学报：自然科学版，1998(1)：18-20．

Yi Jun.The new method for deducing the Dupuit formula[J].Journal of Chongqing Petroleum College:Natural Science Edition,1998(1):18-20.

[9] 郎兆新．油气地下渗流力学[M]．东营：石油大学出版社，2001：2-5．

Lang Zhaoxin.Oil and gas seepage mechanics[M].Dongying:Petroleum University Press,2001:2-5.