缩短自由电子激光放大器饱和长度的研究

，2

(1.西华大学物理与化学学院，四川 成都 610039；2.西南交通大学光电子学研究所，四川 成都 610031)

通过调整电子束的相对论能量因子γ和摇摆器(wiggler或者undulator)的空间周期λw，自由电子激光器的工作波长可实现连续可调，因此自由电子激光器已成为一种红外、太赫兹波段的高功率器件，具有广泛的用途[1-11]。自由电子激光的工作物质是相对论性电子束，由加速器提供，电子束与电磁波的互作用在摇摆器中进行，电子束产生受激辐射，将其一部分动能转换成电磁波的电磁能，使电磁波获得放大[12-14]。红外、太赫兹自由电子激光器的束-波互作用长度通常在1 m以上至十几米。一般说来，工作波长越短，所需电子束能量就越高，摇摆器也越长，器件成本也就越高。例如，工作波长为9～11 μm的我国北京自由电子激光装置，其永磁摇摆器长约2 m，电子束能量为24～28 MeV[5]；而工作波长为794 nm的美国布鲁海文国家实验室(BNL)自由电子激光装置，其永磁摇摆器长达10 m，电子束能量高达101 MeV[1]。显然，如果在获得足够大的输出功率的前提下缩短电子束与电磁波互作用区的长度，那么，所需摇摆器和加速器电子束的长度也就会变短，从而降低摇摆器、加速器及整体器件的成本。目前，缩短束-波互作用长度的主要方法，一是从互作用腔体着手，采用高品质因数的短腔体(short cavity)，使激光波的电磁场分布收拢在有利于与电子束交换能量的区域；二是从电子束着手，采用发射(emittance)和离散(spread)很小的高质量电子束，有利于电子群聚(bunching)，尽快将其动能转换给激光场[13-14]。

本文采用非线性数值模拟方法，研究自由电子激光放大器中关键参数对束-波互作用饱和长度(saturation length)的影响，探索缩短束-波互作用饱和长度的途径。本文所得研究结果，对认识红外、太赫兹自由电子激光的物理特性具有一定学术意义，对降低自由电子激光器成本的工程实践有一定参考价值。

1 数学物理模型

假设电子束的轴线与摇摆器的轴线重合，并选为坐标系的z轴，则圆极化永磁摇摆器的磁场的矢势可表达为

(1)

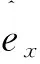
(2)

式中kl=2π/λl，λl、kl、ωl和Al分别是激光的波长、波数、角频率和矢势的振幅。电子束中的任意第i个电子在摇摆器磁场和激光场中的运动，由相对论闵可夫斯基方程决定：

(3)

式中：e和m0是电子的电量和静止质量(物理常数)；γi和vi是第i个电子的相对论能量因子和速度；Bw是摇摆器的磁感应强度；Bl和El是激光的磁感应强度和电场强度。激光场被放大的过程遵从有源波动方程：

(4)

(5)

式中：ε0、μ0和c分别是真空中的介电常数、磁导率和光速(均为物理常数)；ρb和Jb是电子束形成的电荷密度和电流密度。由KMR理论[15]，引入哈密顿函数，经正则变换，可得下面3个标量方程构成的激光波与电子互作用的非线性耦合方程组：

(6)

(7)

(8)

式(6)和(7)描写电子束中序号为i的任意电子(i=1，2，3，…,N)在激光场和摇摆器磁场中的运动状态和能量变化，式(8)描写光波与电子束换能关系。式中各归一化量分别定义为：

此处nb是电子束的体密度，N代表电子束中的所有电子的数目(在数值模拟计算中代表采样电子的数目)。由上述耦合方程组可求出激光场的矢势振幅，从而由其求出激光的功率。

2 束-波互作用饱和长度非线性模拟

本章采用四阶龙格-库塔法数值求解上述非线性微分方程组(6)—(8)，用Fortran语言编程，以一组典型的美国贝克利国家实验室的红外自由电子激光放大器实验设计参数为例[1]，模拟参数对束-波互作用饱和长度的影响。取摇摆器空间周期λw=3.89 cm，幅值Bw=3 016 Ga，长度L=1 m；电子束能量Eb=101.37 MeV，束流Ib=350 A，束斑Rb=0.015 cm；入射光的波长为793 nm，初始功率为10 kW[4]。在束波互作用区内激光功率随纵向位置的演化如图1所示。结果显示：束-波互作用在5.92 m(约6 m)处发生饱和，对应的功率约为1.31 kW。

摇摆器空间周期λw=3.89 cm，幅值Bw=3 016 Ga，长度L=

1 m；电子束能量Eb=101.37 MeV，束流Ib=350 A，束斑Rb=0.015 cm；入射光的波长为793 nm，初始功率为10 kW。

图1 激光功率在束-波互作用区内随纵向位置的演化

摇摆器振幅在3 016 Ga的约±10%范围取值，即Bw=3 300 Ga及2 900 Ga，对应的功率演化曲线如图2所示。可以看到，它们对应的饱和长度分别为5.90 m及5.81 m，相对于摇摆器振幅为3 016 Ga所对应饱和长度5.92 m，最多仅仅缩短了0.11 m，饱和长度减小不到2%，收效甚微。

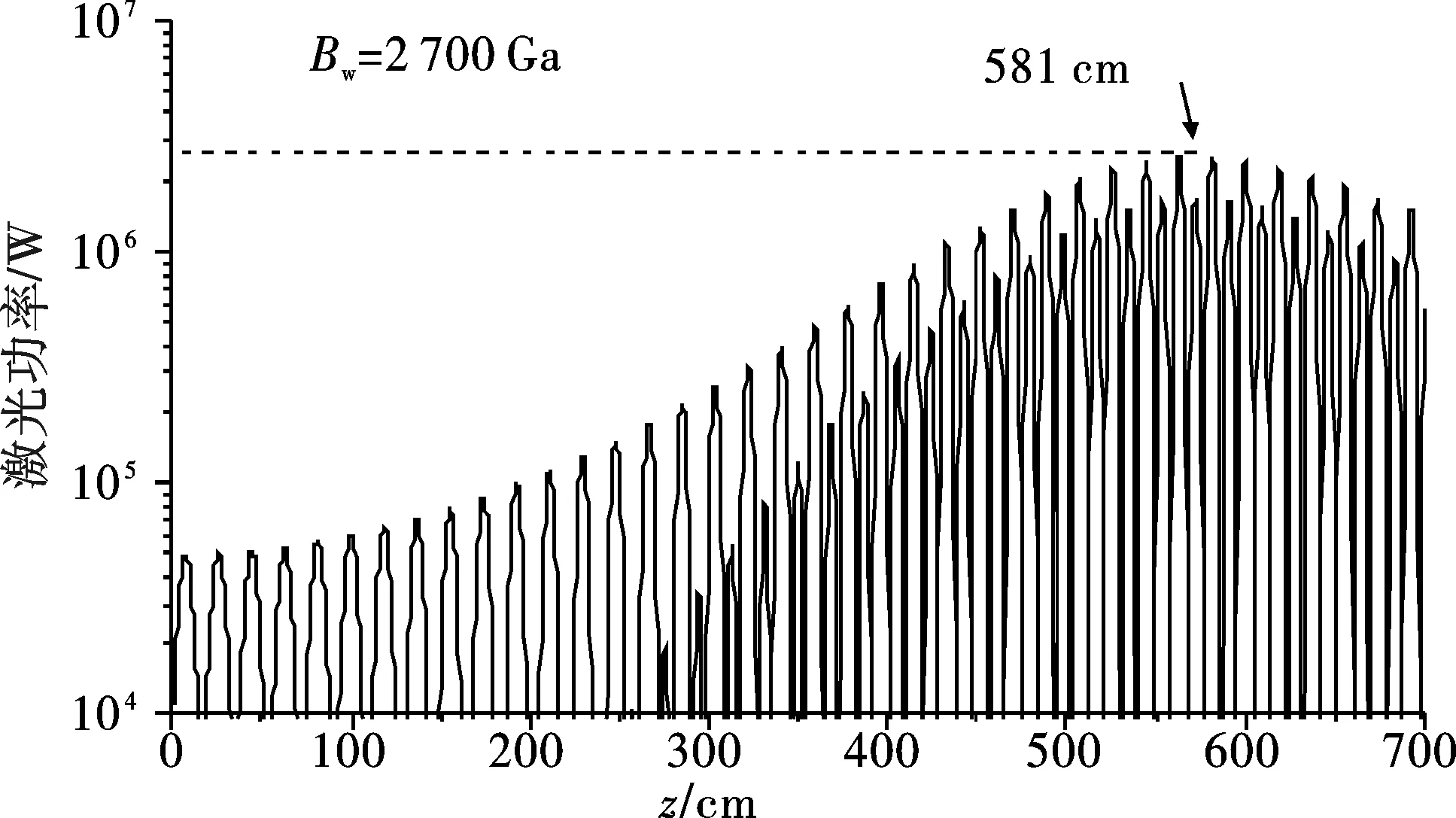
(a)Bw=3 300 Ga，(b)Bw=2 700 Ga，其余参数与图1相同。

图2 不同摇摆器振幅情况下激光功率在束-波互作用区内随纵向位置的演化

照样采用美国贝克利国家实验室的红外自由电子激光放大器实验设计参数为基础数值，为了得到最小的饱和长度和最优的激光功率，通过微调摇摆器周期、电子束能量、激光波长3个参数进行一系列的优化模拟。结果表明，这3个参数的搭配对束-波互作用饱和长度的影响非常显著，可以有效地缩短饱和长度。鉴于优化过程的计算较为繁杂，为节省篇幅和便于阅读，仅把优化结果示于图3，其中优化后的摇摆器周期为3.8 cm，电子束能量为105 MeV，激光波长为853 nm。把图3与图1进行比较，可以发现，摇摆器周期、电子束能量、激光波长三者的优化搭配，使束-波互作用的饱和长度从5.92 m缩短到4.35 m，减小了26.7%(减少1.57 m)，饱和长度大大缩短，而且，对应的饱和功率从1.31 MW提高到了5.93 MW，优化成果收效巨大，为激光器器件减少了成本。

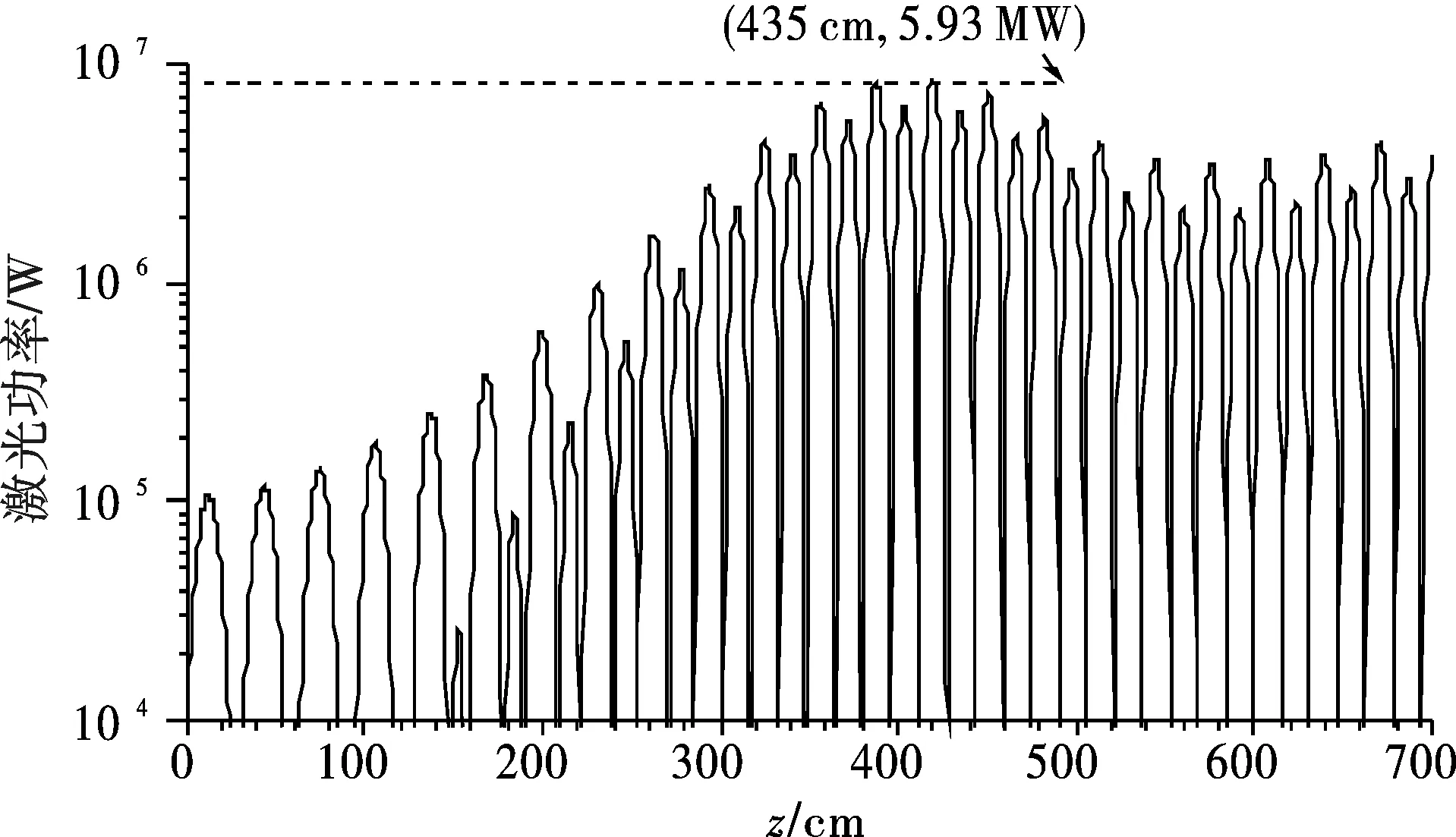
此处摇摆器周期为3.8 cm，电子束能量为105 MeV，激光波长为853 nm，其余参数与图1 相同。

图3 优化摇摆器周期、电子束能量、激光波长后的自由电子激光功率在束波互作用区内的演化

4 结 论

本文采用非线性模型和数值模拟研究了自由电子激光放大器中主要参数对非线性束-波互作用饱和长度的影响，结果表明：

1)摇摆器振幅对束-波互作用的饱和长度影响不大，不能指望通过调整摇摆器振幅的方法来缩短饱和长度。

2)电子束能量、摇摆器周期、激光波长3者的恰当搭配至关重要，可明显缩短束-波互作用的饱和长度并同时提高饱和功率。对于美国贝克利国家实验室的红外自由电子激光放大器实验设计的一组典型的参数而言，我们经过优化模拟建议其将摇摆器周期调为3.8 cm，电子束能量调为105 MeV，激光波长调为853 nm，3个参数的有效搭配使束-波互作用的饱和长度从5.92 m缩短到4.35 m，对应的饱和功率从1.31 MW提高到了5.93 MW，激光器性能大为改善。

本文的计算结果为自由电子激光器的生产和使用过程中参数的有效配置指明了方向，能够有效地降低所需加速器、摇摆器及整体器件的成本。

[1]Wang X J, Freund H P, Harder D, et al. Efficiency and Spectrum Enhancement in a Tapered Free-Electron Laser Amplifier [J]. Physical Review Letters, 2009, 103(15)： 154801.

[2]Vinokurov N. Free Electron Lasers as a High-Power Terahertz Sources[J]. Journal of Infrared, Millimeter, and Terahertz Waves, 2011, 32(10)： 1123-1143.

[3]Kubarev V V, Kulipanov G N, Shevchenko O A, et al. Third Harmonic Lasing on Terahertz NovoFEL[J]. Journal of Infrared, Millimeter, and Terahertz Waves, 2011, 32(10)： 1236-1242.

[4]Asgekar V, Lehnert U, Michel P. A Tapered Undulator Experiment at the ELBE far Infrared Hybrid-Resonator Oscillator Free Electron Laser[J]. Review of Scientific Instruments, 2012, 83(1)： 015116.

[5]Xie J, Zhuang J, Huang Y, et al. The Saturation of the Beijing FEL [J]. Nuclear Instruments and Methods in Physics Research Section A： Accelerators, Spectrometers, Detectors and Associated Equipment, 1995, 358(1)： 256-259.

[6]金晓, 黎明, 许州, 等. 中国工程物理研究院远红外自由电子激光实验研究[J]. 高能物理与核物理, 2008 (增刊1)： 96-98.

[7]Zhang S C. Focusing Effect and Modulation Mechanism of the Beam Self-Fields on the Electron’s Larmor Rotation in a Free-Electron Laser with an Axial Guide Magnetic Field[J]. Physics Letters A, 2013, A377：319-322.

[8]Ginzburg N S, Peskov N Y. Nonlinear Theory of a Free Electron Laser with a Helical Wiggler and an Axial Guide Magnetic Field[J]. Physical Review Special Topics-Accelerators and Beams, 2013, 16(9)： 090701.

[9]Ji Y P, Wang S J, Xu J Y, et al. Effect of Normalized Plasma Frequency on Electron Phase-Space Orbits in a Free-Electron Laser [J]. Chinese Physics B, 2013, 23：024103

[10]徐勇根, 张世昌, 王时建, 等. 拉曼型自由电子激光器中相对论电子运动稳定性的比较研究[J]. 物理学报, 2013, 62：084104

[11]Huang X L, Wang S J, Xu Y G, et al. Equilibrium Electrons in Free-Electron Lasers with a 3D Helical Wiggler and a Guide Magnetic Field： Nonlinear Simulations [J]. Physical Review Special Topics-Accelerators and Beams, 2012, 15(12)： 120702.

[12]张世昌.自由电子激光导论[M]. 成都：西南交通大学出版社, 1993.

[13]Marshall T C. Free-electron lasers[R]. USA：Columbia Univ，1985.

[14]Saldin E L, Schneidmiller E A, Yurkov M V. The Physics of Free Electron Lasers[M]. Germany ：Springer Verlag, 2000.

[15]Kroll N M, Morton P L, Rosenbluth M W. Free-Electron Lasers with Variable Parameter Wigglers[J]. Quantum Electronics, IEEE Journal of, 1981, 17(8)： 1436-1468.