玻璃幕墙风荷载设计研究
王敬丽,李 宁
(河北工程大学土木工程学院,河北邯郸056038)
所谓的建筑幕墙就是由支承结构体系与面板组成的、可相对主体结构有一定位移能力、不分担主体结构所受作用的建筑外围护结构或装饰性结构。
随着玻璃幕墙这种外装修围护结构的兴起,国内外高层建筑采用玻璃幕墙的迅速增多,玻璃幕墙的建筑技术发展也十分迅速,如:北京长城饭店(22层,83.85 m高)、北方国际传媒中心(26层,104.3 m高)、芝加哥西尔斯大厦(110层,442 m高)、芝加哥汉·考兰大厦(100层,344 m高)、德国慕尼黑奥林匹克体育馆等,许多著名的建筑都以玻璃幕墙为外部装修。
作为一种新型产业,玻璃幕墙的结构设计也是研究者主要的研究对象,其主要问题是抗风和抗震设计,但相对于抗震来说,风荷载是玻璃幕墙所受的主要荷载。故本文通过有限元的计算方法,对玻璃幕墙的三种形式分布进行了抗风设计的对比研究。
1 玻璃幕墙的三种构造形式
玻璃幕墙形式各异, 设计计算所依据的力学模型也不尽相同, 因此, 有限元的计算方法在幕墙设计计算过程中被广泛采用。按照玻璃板块的支承形式进行分类, 玻璃幕墙可分为框支承幕墙、点支承幕墙以及全玻幕墙。下面分别介绍玻璃幕墙的三种不同构造形式。
框支承玻璃幕墙(frame supported glass curtain wall): 玻璃面板四周由金属框架支承的玻璃幕墙(图1)。框支承玻璃幕墙最外面是玻璃板块, 它支承在铝合金横梁上, 横梁与立柱连接, 立柱则悬挂在主体结构上。上、下层立柱通过活动接头连接, 可以相对移动, 以适应温度变形和楼层的轴向压缩变形。按幕墙形式分:明框玻璃幕墙、隐框玻璃幕墙、半隐框玻璃幕墙;按幕墙安装形式分:单元式玻璃幕墙、构件式玻璃幕墙。
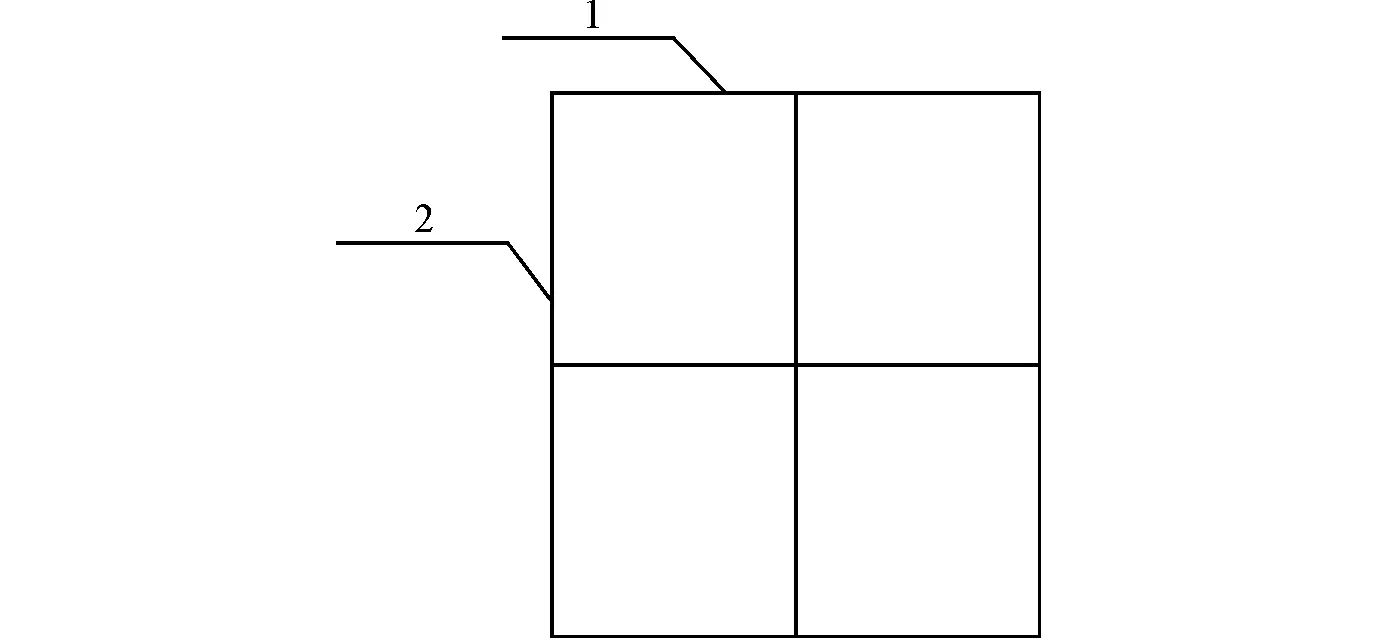
(1—横梁;2—立柱)图1 框支承玻璃幕墙截面示意
全玻幕墙(full glass curtain wall):由玻璃肋和玻璃面板构成的玻璃幕墙,其结构形式如图2所示。全玻玻璃幕墙的结构有单肋和双肋两种形式。全玻玻璃幕墙的板面不得与其他刚性材料直接接触。其板面与装修面或结构面之间的空隙不应小于8 mm,且应采用密封胶密封。
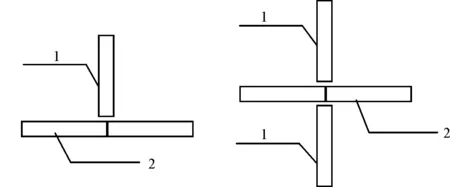
(a)单肋 (b)双肋(1—玻璃肋;2—玻璃面板)图2 全玻幕墙玻璃肋截面示意
点支承玻璃幕墙(point-supported glass curtain wall):由玻璃面板、点支承装置和支承结构构成的玻璃幕墙。点支式玻璃幕墙的玻璃面板一般仅由支承点支承, 通常为四角支承(图3), 也有六点或八点支承[2]。面板玻璃一般采用钢化夹胶玻璃, 也有少数采用中空钢化玻璃。
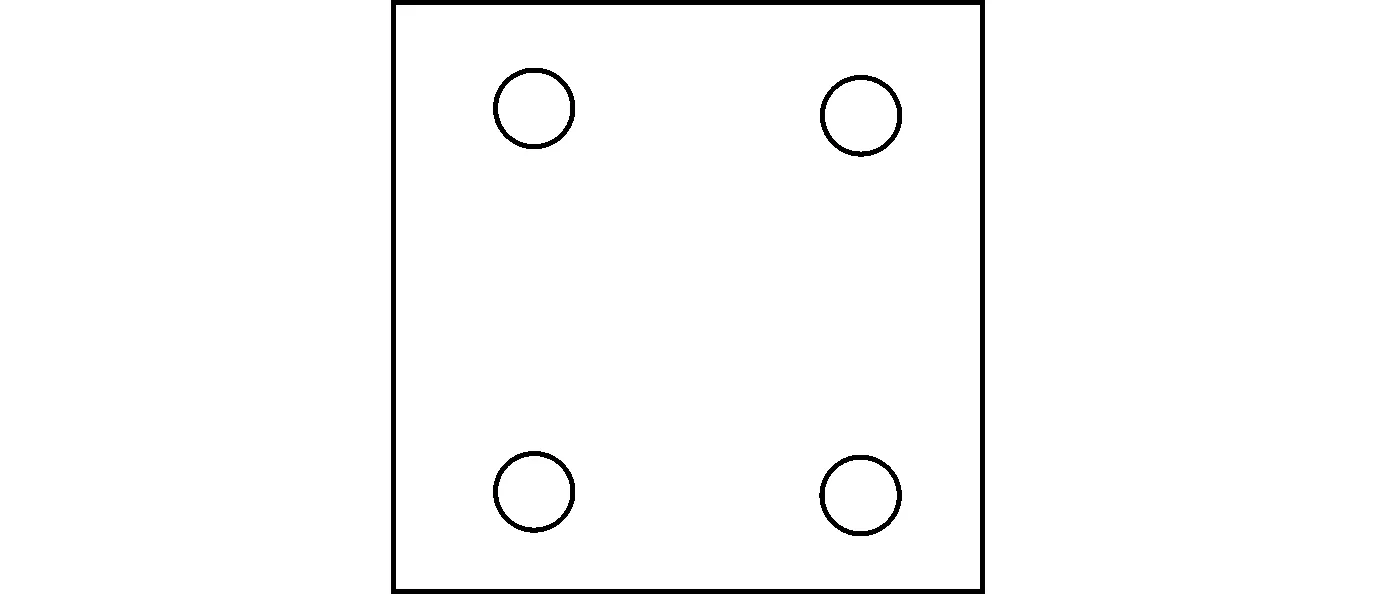
图3 四点支承玻璃幕墙示意
2 有限元计算方法
本文根据模拟风压作用下三种不同安装结构的玻璃幕墙结构各自的受力特点, 对其分别建立了不同的玻璃幕墙结构的有限元模型。
2.1 框支承玻璃幕墙的有限元模型简化
根据框支承玻璃幕墙的受力特点,设定立柱的两端与静压箱之间的连接视为铰接, 而梁柱间的连接为刚性连接,本文采用弹性杆单元通过改变其刚度来模拟立柱上下两端节点处的半刚性状态[7]。模型自由度的约束依据玻璃幕墙的安装结构形式来实现。立柱悬挂结构体上, 杆件上端固定, 下端释放其轴线方向的自由度, 以减小立柱轴向由于温度变化而产生的应力。横梁两端与立柱固定连接,玻璃板块四边支撑于立柱与横梁上。在对横梁、立柱进行有限元计算时采用考虑轴向力和剪切变形的空间梁单元, 对玻璃采用弹性薄壳单元。
2.2 全玻玻璃幕墙的有限元模型简化
对于全玻玻璃幕墙的结构形式,面板玻璃通过胶缝与玻璃肋相连结时,面板可作为支承于玻璃肋的单向简支板设计。面板与玻璃肋的连接按铰接设计。有限元计算采用弹性-大变形有限元分析模块,计算过程中可以忽略玻璃胶缝的宽度。
2.3 点支承玻璃幕墙的有限元模型简化
点支承玻璃幕墙的玻璃面板由支承点支承, 通常为四点支承、六点支承、八点支承等,在风荷载作用下,其受力可简化为四角简支受力或多点简支受力。由弹性薄板的小挠度弯曲变形理论,点支承玻璃面板的弯矩与挠度可采用弹性薄板的有限单元法程序计算[4]。
在进行计算的过程中,风荷载的施加以均布荷载的形式垂直作用于各个玻璃板块的表面。
完成上述有限元计算前处理工作后, 进入ANSYS的求解模块(图4), 选择分析类型为静态分析, 进行解算,如图5所示为三种玻璃幕墙结构分别在ANSYS软件中的计算流程图。求解完成以后, 在后处理模块中查看分析结果,然后进一步对三种安装结构形式进行对比分析,进而做出进一步的总结分析。
图4 ANSYS软件进行中的模型输入
3 实例计算及结构分析
如将玻璃幕墙的平板玻璃选取为2 m×2 m的方形平板面,板厚为1.4 cm。现在在玻璃板面的垂直方向上施加0.14
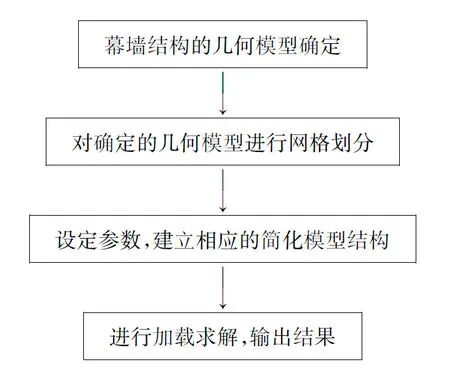
图5 幕墙结构在有限元程序中计算的流程
N/cm2的风压力。本例中,框支承玻璃幕墙选用常用的明框玻璃幕墙形式,全玻玻璃幕墙选用单肋玻璃幕墙的结构形式,点支承玻璃幕墙选用四点支承的结构形式。
利用上述方法对三种不同的安装构造形式进行有限元计算程序求解,从计算后可获得各幕墙结构形式的最大弯曲应力值,见表1。

表1 各种幕墙结构形式最大弯曲应力 N/cm2
通过有限元计算程序求解取得的最大应力值表中可以看出,框支承玻璃幕墙的最大应力弯曲值远小于规范玻璃的允许应力。而全玻玻璃幕墙和点式玻璃幕墙主应力远远超过了设计的允许应力,而且点式玻璃幕墙是极其集中的破坏应力,对结构的破坏性能较强。
4 结束语
从以上的分析中可知,有框式玻璃幕墙是相对较安全的结构形式。虽然,全玻玻璃幕墙和点式玻璃幕墙具有外形美观、通透性好等特点,但是由于全玻玻璃幕墙和点式玻璃幕墙结构形式易产生极其严重的破坏应力,故在以后的选用和施工中需要特别的注意。
[1] 李创第,管昌生,李桂青,等.高层建筑玻璃幕墙的风压和风振计算[J].广西工学院学报,1996,7(4):26-31
[2] 童丽萍,李明.风荷载作用下玻璃幕墙结构的受力分析与计算[J].工业建筑,2000,30(4):27-30
[3] 洪天华,李宏男.风荷载作用下单层平面索网体系点支式玻璃幕墙的动力性能研究[J].防灾减灾工程学报,2008,28(2):156-162
[4] 韦林,蒋伟.风荷载作用下点支式玻璃幕墙的受力分析[J].建筑施工,2006,28(5):401-403
[5] 刘忠伟,孙加林,洪彦若.点接式玻璃幕墙抗风压性能[J].北京科技大学学报,1999,21(5):472-475
[6] 吴奕生,陈海,郭金基.点式玻璃幕墙有限元法的计算[J].机电工程技术,2003,32(4):48-49
[7] 史宝军,尹晓江,张瑞军,等.玻璃幕墙结构力学性能试验分析与数值模拟[J].山东建筑大学学报,2006,21(6):474-479

