圆柱度误差可视化评定系统
黄海军, 周 顺
(华东交通大学 轨道交通学院, 江西 南昌 330013)
圆柱度误差可视化评定系统
黄海军, 周 顺
(华东交通大学 轨道交通学院, 江西 南昌 330013)
为了实现圆柱度误差的可视化评定,采用最小二乘和最小区域两种评定方法,根据所建立的数学模型,采用LabVIEW作为软件平台,构建了圆柱度误差测量评定系统。系统具有数据保存、图形显示以及图形功能扩展能力。
圆柱度误差; 最小二乘法; 最小区域法; 虚拟仪器
0 引 言
圆柱度误差是评价轴类零件形状精度的重要指标之一,准确地测量和评定零件的圆柱度误差,不但可以作为零件验收合格的依据,还可以为提高零件加工精度提供可靠的依据[1]。
为了提高检测的精度和效率,设计了一套基于虚拟仪器的圆柱度误差可视化评定系统,实现了圆柱度误差最小二乘法和最小区域法软件的评定。
1 系统构成
1.1硬件平台
形状误差评定系统的硬件平台由工作台、电感式位移传感器(DGB-5B)、采集卡(USB-4711A)、计算机构成[2]。工作台如图1所示。
将零件对顶夹在顶尖4上,夹有电感式位移传感器的磁性表座放在X轴方向工作台2上,并固定好传感器的测头与零件接触,转动顶尖,可以检测到任意截面一周轮廓数据,转动Z轴方向手柄,改变传感器的位置,再转动顶尖,测取新一组圆的轮廓数据,测量若干组数据,评定圆柱度。
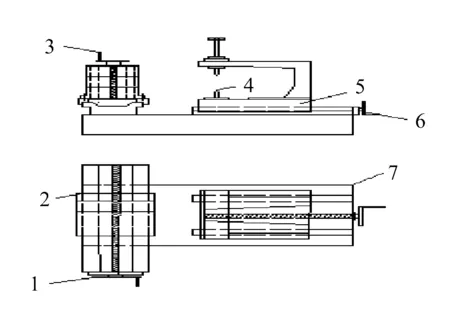
1.X轴方向手柄; 2.X轴方向工作台; 3.Z轴方向手柄;4.可转动顶尖; 5.Y轴方向可移动工作台;6.Y轴方向手柄; 7.底座
1.2数学模型
1.2.1 最小二乘法评定原理
建立空间直角坐标系OXYZ,Z坐标轴为测量时被测件的回转轴线,将被测圆柱面分成与Z坐标轴垂直的彼此等距的4个采样截面,XOY坐标平面与被测实际圆柱的各采样截面的对称中心相重合,在每个采样截面内的被测轮廓上有37个等角度间隔的采样点Pij(Δrij,θij,Zi)(i=1,2,3,…,m;j=1,2,3,…,n),L为被测实际圆柱表面的最小二乘圆柱面的轴线[3],它通过XOY平面上的点O1(a,b,0),R为最小二乘圆柱面半径。最小二乘法评定圆柱度误差如图2所示。
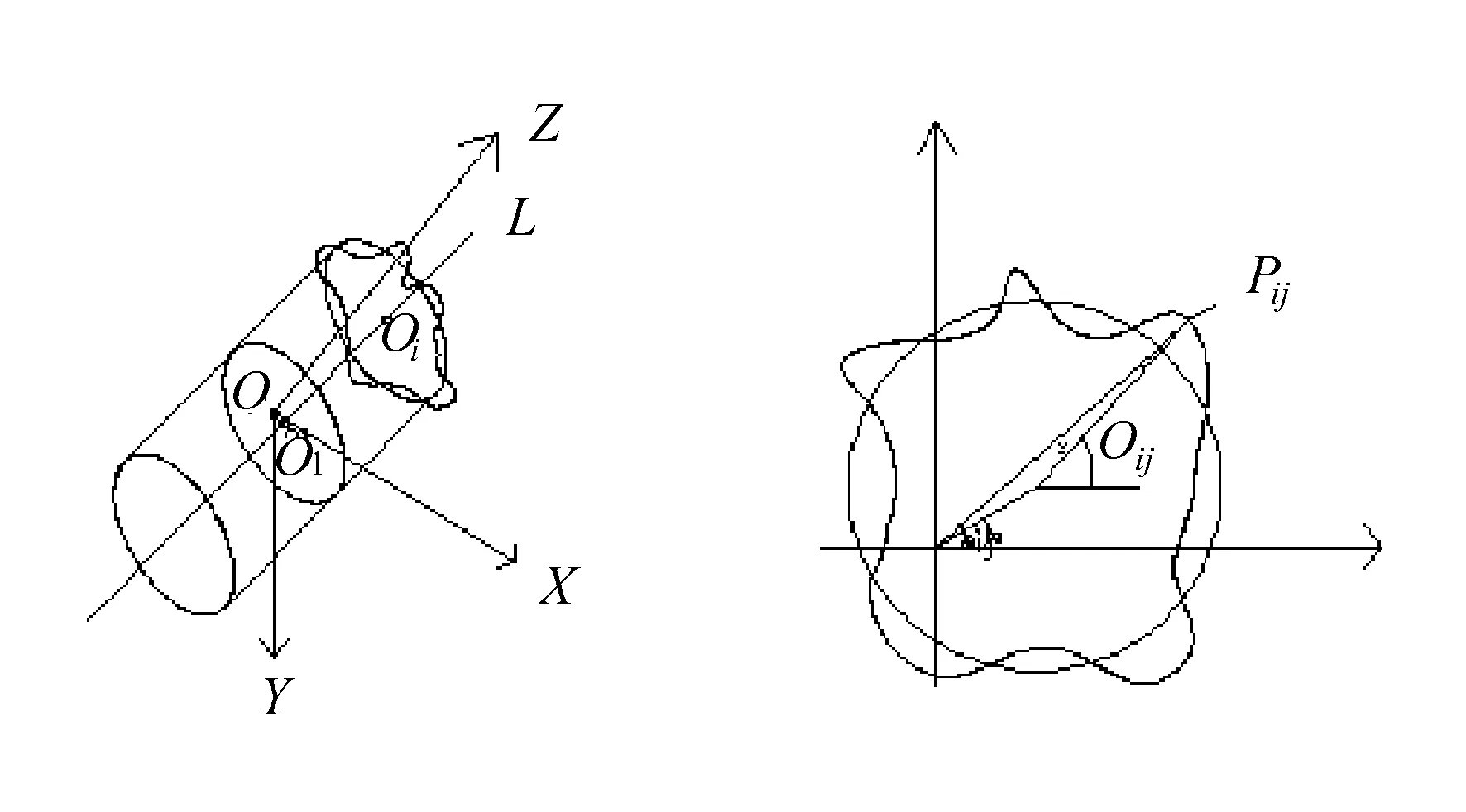
图2 最小二乘法评定圆柱度误差
假设轴线L的方程为
(1)
令c=0,n=1,则m=z,可以得到:
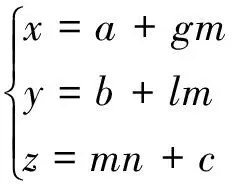
(2)
L与第i个采样截面的交点为Oi(ai,bi,zi),则
(3)
根据图中的几何关系和最小二乘法原理[4],可推出
(4)
(5)
(6)
圆柱度误差值:
(7)
1.2.2 最小区域法评定原理
利用最小区域法评定圆柱度误差,根据求出的最小二乘圆柱面的轴线方程来作为包容实际圆柱面的两个包容圆柱面的同一轴心线,这样再根据最小区域法评定圆柱度误差的原理,两个包容圆柱面的半径差就是圆柱度误差,即所有点到轴线的距离的最大值减去最小值[5]。
求出轴心线的方程:
(8)
点到空间直线的距离可以先求出一垂直于直线并过该点的平面,然后再求出这一平面与该直线的交点,点与点之间的距离之差就是圆柱度的误差。
所以误差为:
(9)
1.3程序设计
1.3.1 最小二乘法
根据数学模型,利用LabVIEW这个软件的功能模块进行编程[6]。具体程序编辑步骤为:建立4个文件输入路径,调用读取数据模块,每一组数据编辑程序采取36个数据,根据数学模型(1)~模型(5),求出最小二乘圆柱的轴线方程,做出最小二乘圆柱面,根据数学模型(6)和模型(7),求出圆柱度误差。
截取4个圆周的数据,每个圆周提取36个点,根据式(1)~式(6),在LabVIEW中调用函数二维数组模块、文件输入模块、数学运算模块、二维图形模块、XY波形图公式、公式节点模块,如图3和图4所示。
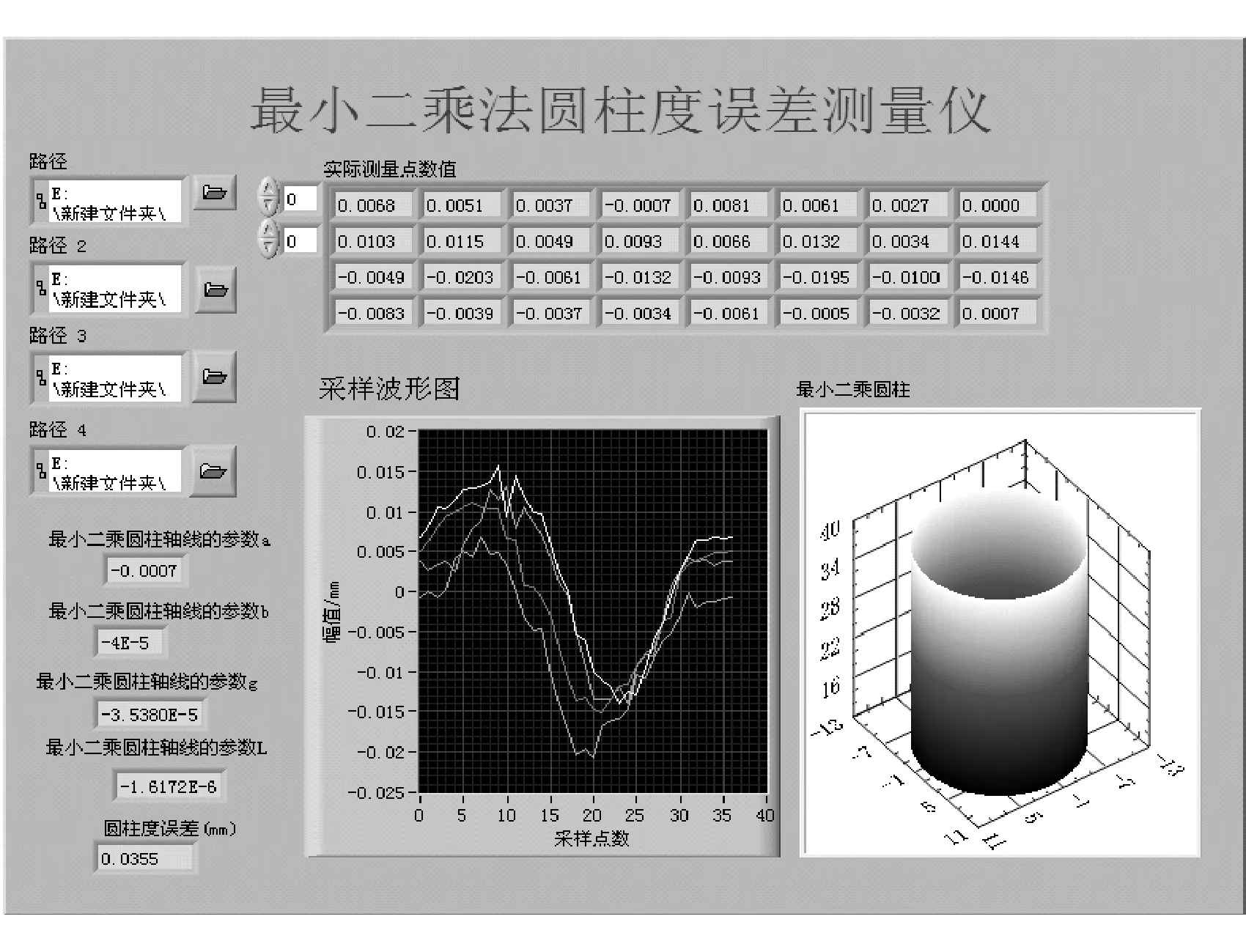
图3 圆柱度误差最小二乘法面板
可得到4组轮廓数据及波形图、最小二乘圆柱三维图、最小二乘圆柱轴线参数、最小二乘法圆柱度误差是0.035 5 mm。
图4中,根据数学模型(1)~模型(9),求出圆柱度误差,所编程序如图5所示。
最小二乘圆柱图形框图程序的编写是调用了公式节点模块和三维图形模块,如图6所示。
1.3.2 最小区域法
根据数学模型,利用LabVIEW软件的功能模块进行编程。步骤为:建立4个文件输入路径,调用读取文件模块,根据4组数据做出实际圆柱面,根据数学模型(8)~模型(9),利用最小二乘圆柱轴线,求点到直线的距离,求出圆柱度误差。
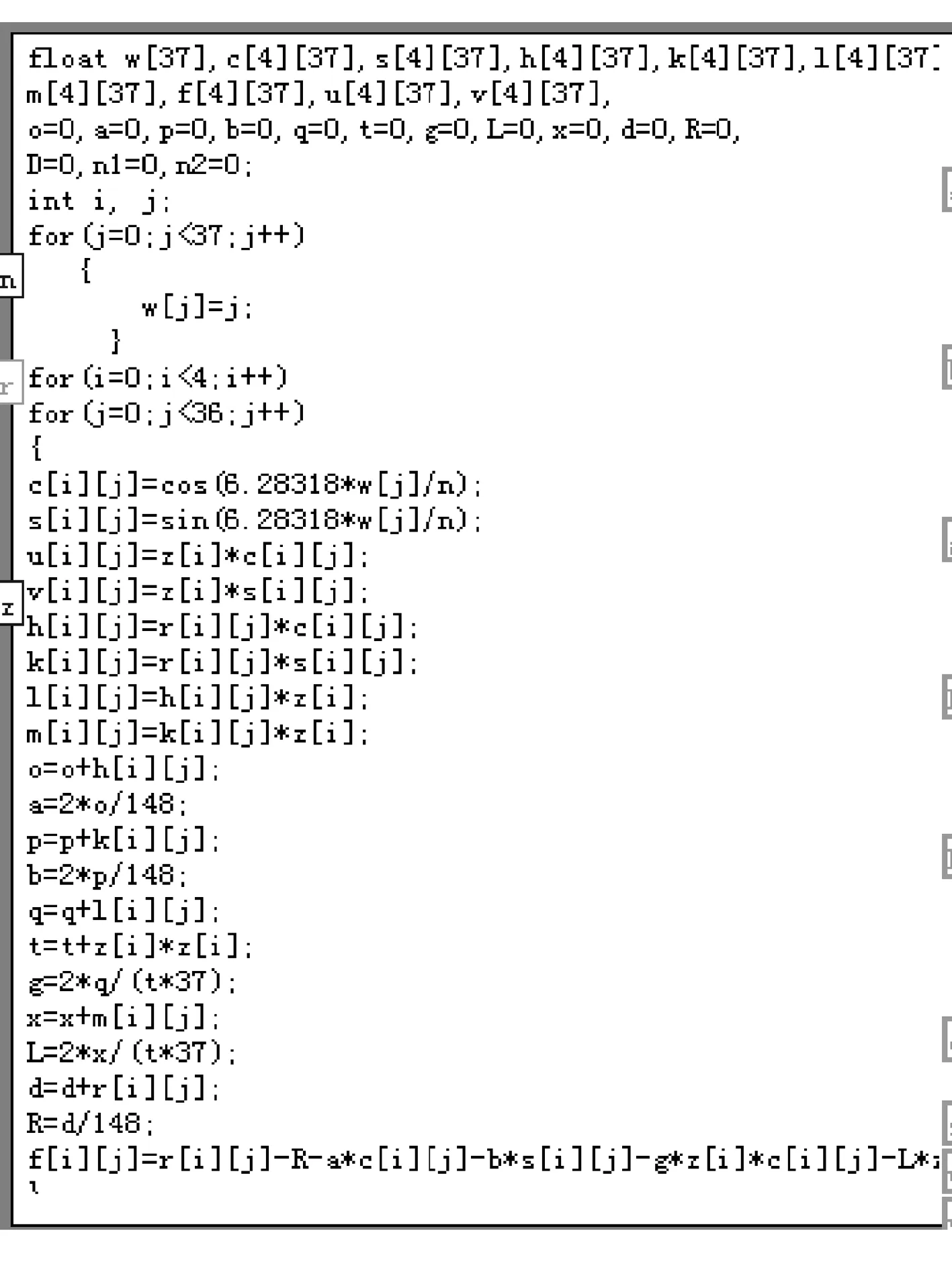
图5 最小二乘法圆柱度误差程序
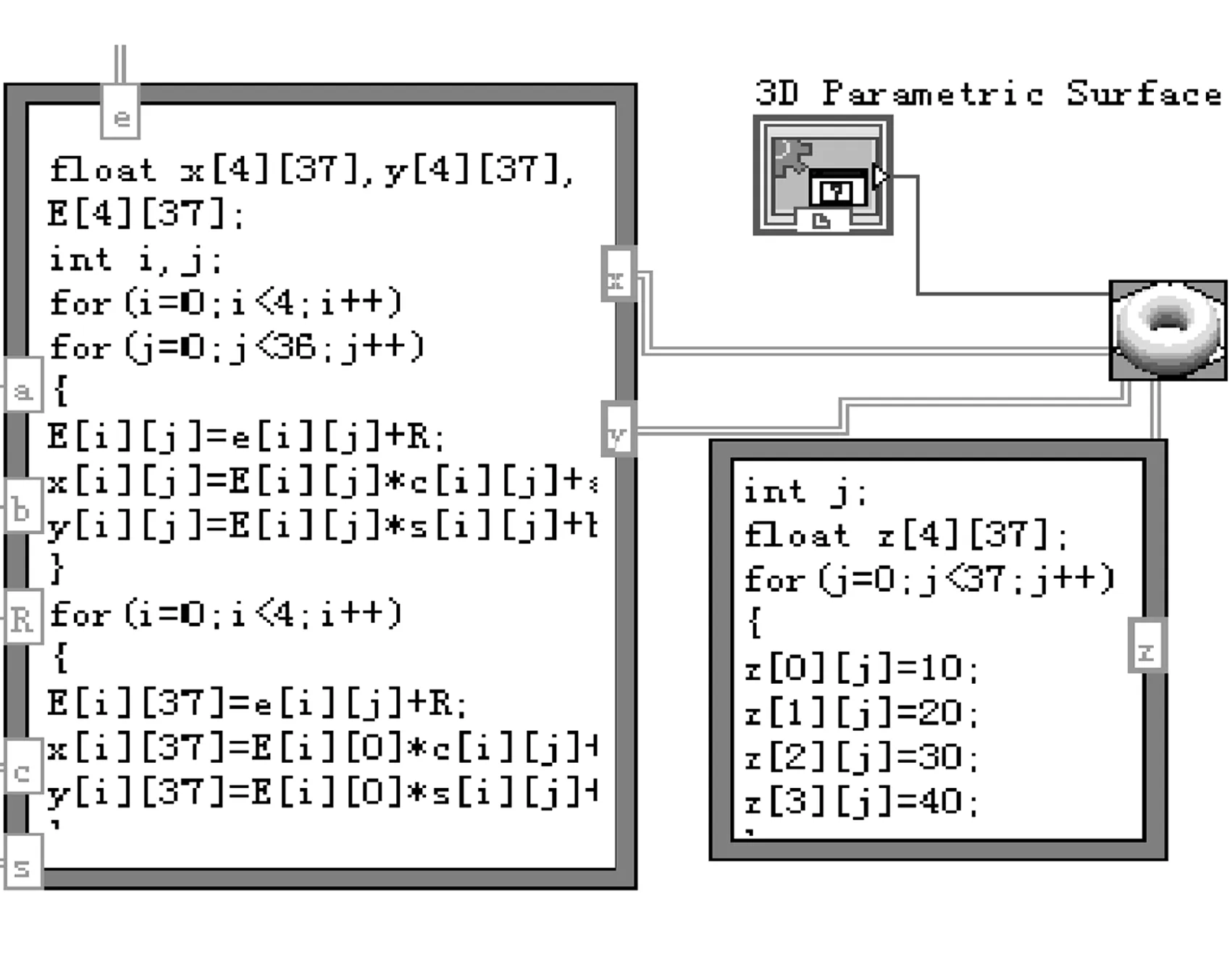
图6 最小二乘圆柱面框图程序
截取4个圆周的数据,每个圆周提取36个点,根据式(8)和式(9),在LabVIEW中调用二维数组函数、文件输入函数、数学运算函数、二维图形函数、XY波形图公式、公式节点模块,如图7所示。
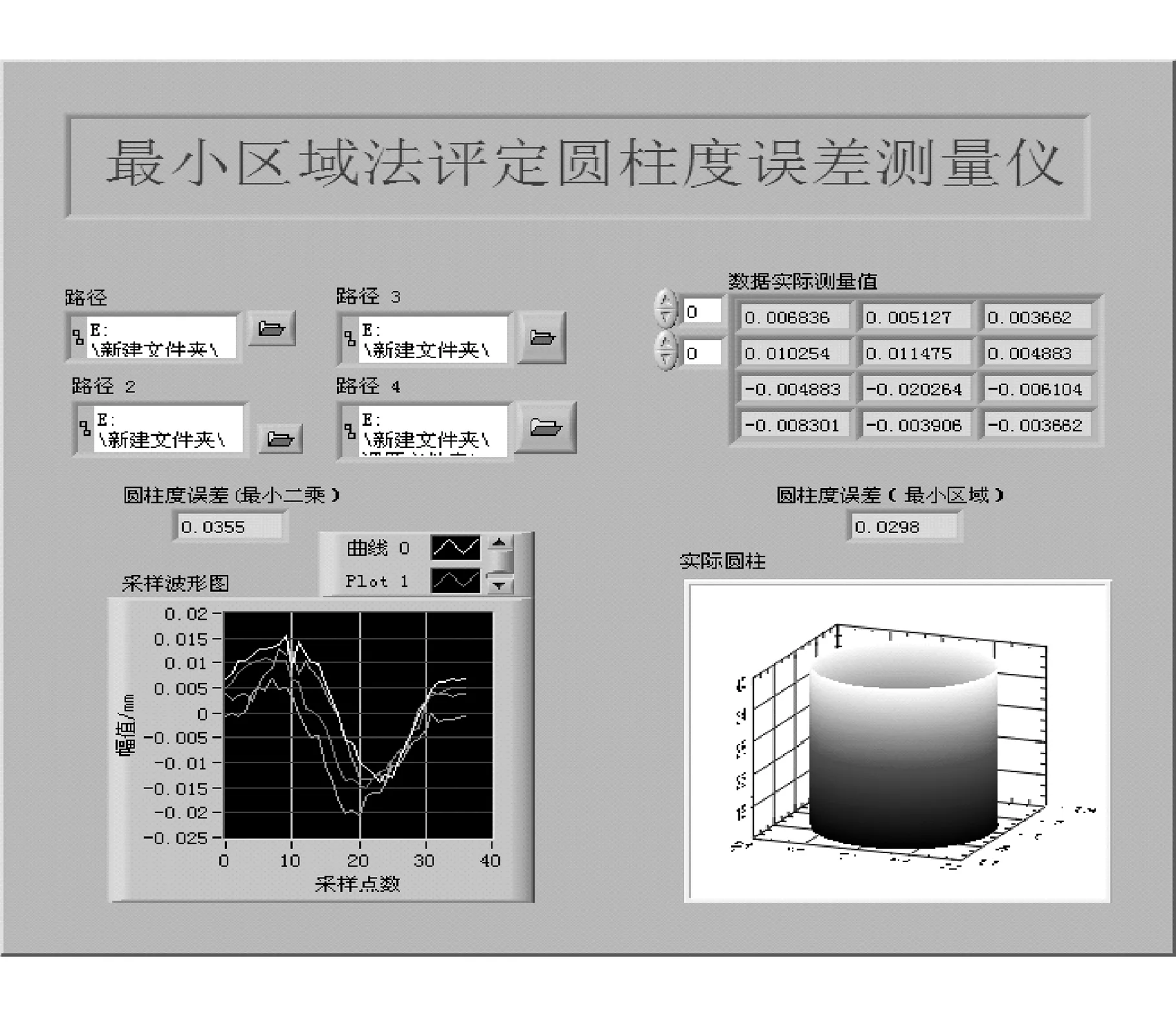
图7 圆柱度误差最小区域法前面板
可得到4组轮廓数据及波形图,实际圆柱三维图、最小区域法圆柱度误差是0.029 8。
实际圆柱面轮廓三维显示框图程序的编写,如图8所示。
最小区域法圆柱度误差框图程序的编写,实现了式(9)的编辑,如图9所示。
2 实验测试
通过与三坐标机测量机的对比,对提出的算法和编写的软件进行验证,结果见表2。
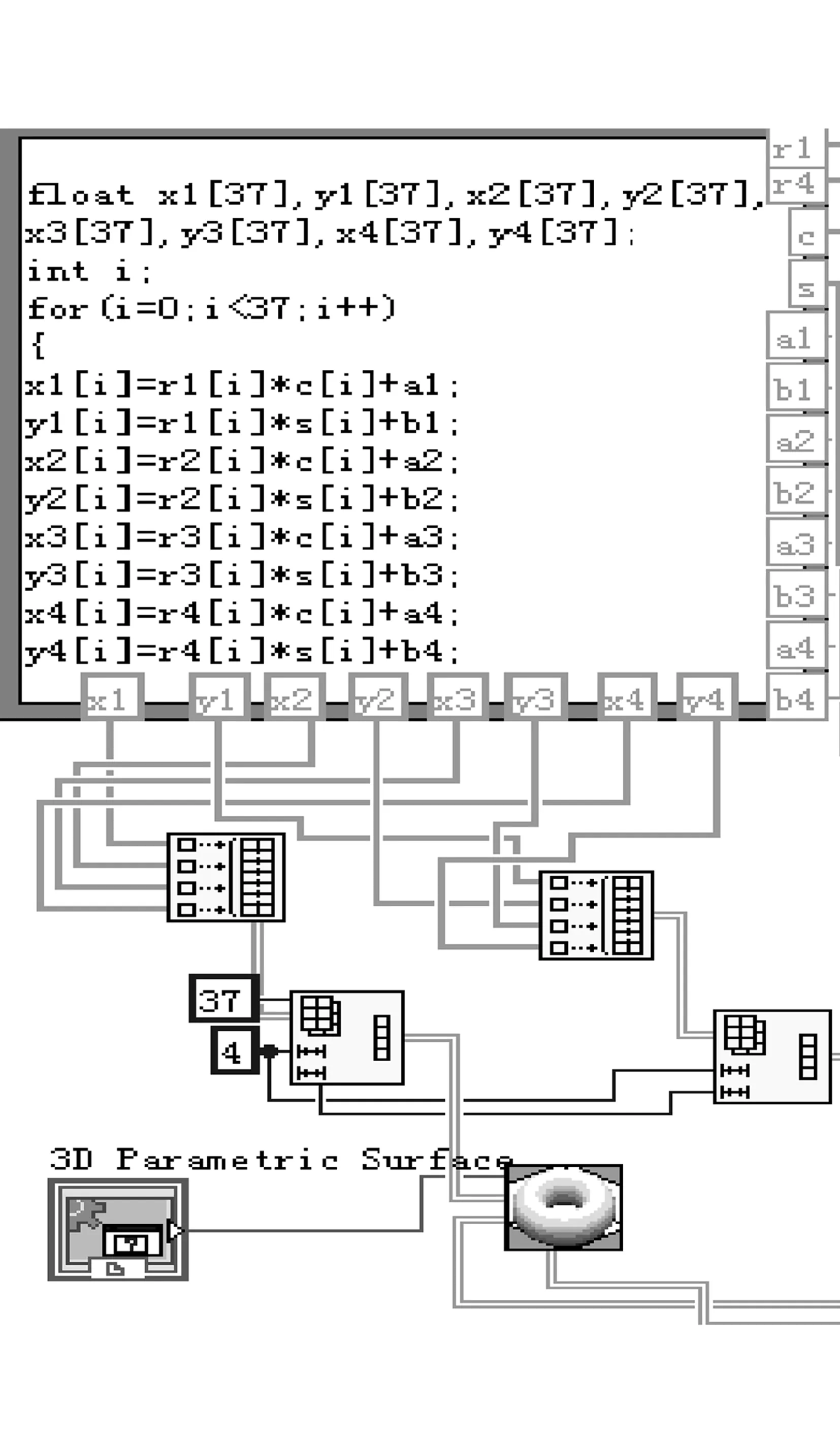
图8 实际圆柱面轮廓框图程序

图9 最小区域法圆柱度误差框图程序

表2 测量结果的对比
所设计的评定圆柱度误差系统与三坐标测量机结果相似,验证了圆柱度误差测试评定系统的有效性。
3 结 语
基于虚拟仪器评定系统,用最小二乘法、最小区域法进行圆柱度误差的评定,可以快速、准确地完成数据采集、处理和误差分析,并给出三维曲面图和圆柱度误差值,实现测试过程的自动化、数字化、可视化,为实际在线监测和质量判别提供依据[7]。
[1] 姜涌,胡教,姬翔.基于虚拟仪器的圆度误差测量系统[J].仪器仪表学报,2007,28(4):643-645.
[2] 黄松岭,吴静.虚拟仪器设计基础教程[M].北京:清华大学出版社,2008.
[3] 雷贤卿,李言.圆柱度三点法测量技术[J].仪器仪表学报,2007,28(5):944-951.
[4] 靳国栋,刘衍聪,牛文杰.距离加权反比插值法和克里金插值法的比较[J].长春工业大学学报:自然科学版,2003,24(3):53-57.
[5] 廖念钊,莫雨松.形状误差测量[M].北京:计量出版社,2010.
[6] 申焱华.LabVIEW入门与提高范例教程[M].北京:中国铁道出版社,2006.
[7] 万文.平面度误差可视化系统研究[J].制造业自动化,2011,33(12):34-35.
Visualization evaluation system for a cylindricity error
HUANG Hai-jun, ZHOU Sun
(School of Rail Transit, East China Jiaotong University, Nanchang 330013, China)
In order to realize the visual evaluation for the cylindricity error, we apply both the Least Square and Minimum Zone method to build a cylindricity error measurement and assessment system with LabVIEW based on the established mathematical model. The system is with the functions of data storage, display and scalability.
cylindricity error; least square method; minimum zone method; virtual instrument.
2014-05-25
江西省教育厅基金资助项目(GJJ14359)
黄海军(1969-),男,汉族,江西樟树人,华东交通大学实验师,主要从事轨道车辆轮轴检测技术方向研究,E-mail:huanghaijun@ecjtu.edu.cn.
TH 39
A
1674-1374(2014)04-0389-05

