发电机用磁性槽楔对电磁参数与性能的影响

，，，

(哈尔滨理工大学电气与电子工程学院，黑龙江哈尔滨 150040)

0 引言

电机能效水平的提高对于节约能源、降低成本具有重要意义。由于嵌线工艺的要求，隐极同步发电机定子槽型普遍采用矩形开口槽的设计方案。然而这种结构会导致气隙齿磁导变化加剧，电机损耗增加、效率降低、振动噪声增大。为此可采用磁性槽楔以改进电机参数与电机性能。磁性槽楔是一种电机上使用的导磁槽楔。目前经过应用的磁性槽楔主要有模压磁性槽楔、磁性板槽楔、磁性引拔槽楔等。

本文以一台1MW隐极同步发电机为研究对象，从理论计算和软件仿真两方面结合分析相对磁导率为1的非磁性槽楔和相对磁导率为3到9的磁性槽楔对电机气隙磁密分布、发电机端电压波形、气隙系数、励磁电流、短路比对比分析了电磁参数和电机性能随磁性槽楔导磁性能的变化情况，另外结合磁性槽楔受电磁力情况综合分析。为磁性槽楔的选用提供一定的参考价值。

1 发电机数学模型与物理模型

1.1 基本假设

样机为隐极同步发电机，其具体参数为：额定功率1MW；额定电压400V；频率50Hz；额定转速1 000rpm；极数6；定子外径850mm；定子内径590mm；转子外径581mm；气隙4.5mm；有效铁心长580mm；定子槽型为矩形开口槽，槽数为90；转子槽型为梨形槽，实槽数为48，虚槽数为72；转子装有全阻尼绕组。

为简化计算，做几点假设[2]：(1)忽略磁性槽楔的导电性，不计由此产生的电气损耗；(2)忽略磁饱和对槽楔相对磁导率的影响，认为槽楔相对磁导率为常数。

1.2 边值问题

基于假设，在二维场中，矢量磁位只有轴向分量，则电机的瞬态场数学模型为[3]

(1)

式中，Az—矢量磁位的轴向分量；Js—源电流密度；μ—磁导率；ρ—电阻率。在求解区域的边界面上，满足的边界条件见式(2)，二维有限元物理模型求解区域如图1所示。

(2)

图1 二维场求解区域模型

2 对气隙磁场和端电压的影响

2.1 对气隙磁场的影响

电机旋转时气隙磁导的不断变化会造成气隙磁密不均匀，产生高次谐波。由气隙磁密谐波分解得到的各高次齿谐波是引发表面损耗和脉振损耗的重要原因[6]。计算样机的气隙磁密分布如图2所示。

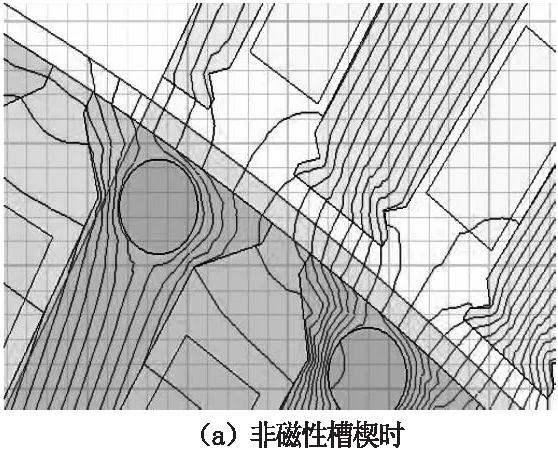
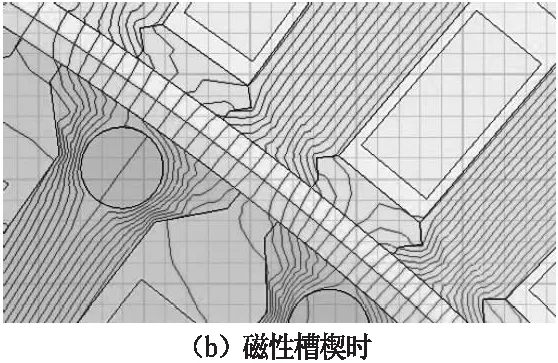
图2 气隙磁通分布图

图2(a)和图2(b)分别采用非磁性槽楔和相对磁导率为5的磁性槽楔在电机空载稳定运行时的气隙磁密分布。图2(a)主磁通经过定子齿、气隙后进入转子，定子槽口附近的气隙磁密分布较少，气隙磁密分布不均；图2(b)则表明使用磁性槽楔后，槽口处的磁阻减小了，有更多的磁通将经过磁性槽楔到达转子。可见，使用磁性槽楔后，气隙磁密更加均匀。图3为使用非磁性槽楔和相对磁导率为5的磁性槽楔气隙磁密分布及谐波分析对比图。

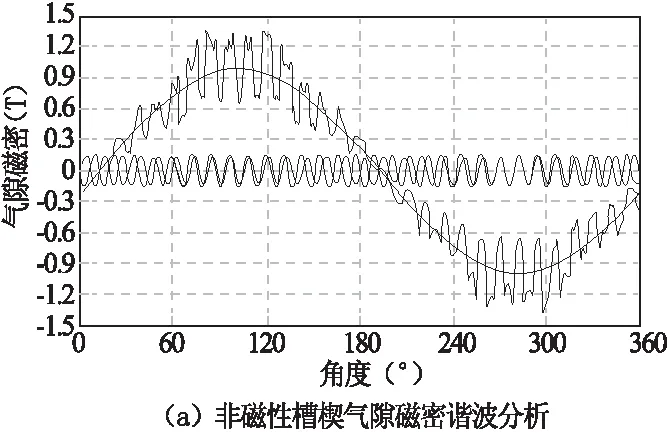
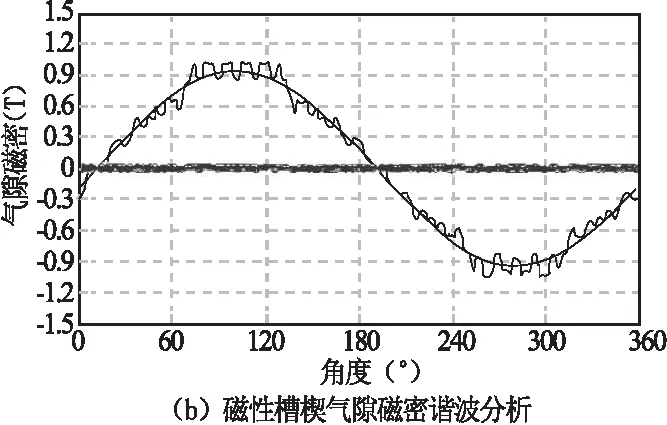
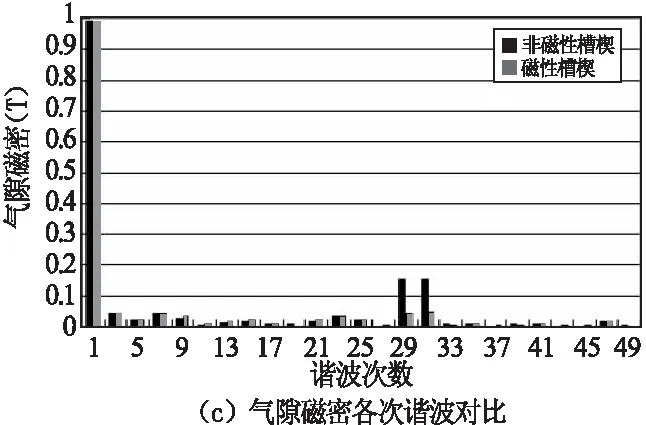
图3 空载气隙磁密谐波分析

可以看出图3 (a)中顶部和底部呈锯齿状，波形峰值约为1.35T，波形底部约为0.62T。图3(b)使用磁性槽楔后，气隙磁密波形峰值约为1.1T，波形底部约为0.9T，脉振幅值的变化见表1。

表1 脉振幅值

图3(c)为非磁性槽楔与磁性槽楔气隙磁密谐波幅值的对比，可以更明显的看出使用磁性槽楔后，气隙磁密中各次谐波幅值减小，其中29次和31次齿谐波幅值的下降尤其明显。

2.2 对发电机端电压的影响

图4为电机空载起动至稳定运行时，使用非磁性槽楔和相对磁导率为5的磁性槽楔发电机端电压波形及谐波分析对比图。

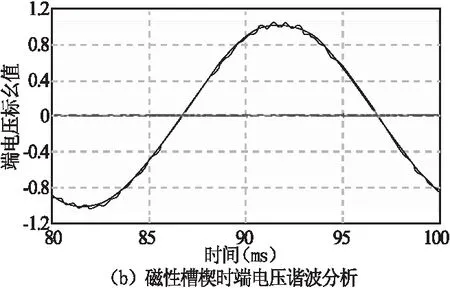
图4 空载发电机端电压波形分析

可以看出使用磁性槽楔后，端电压波动幅值减小，表明由于气隙不均匀而产生的电压波形的畸变得到改善。图4(b)为端电压各次谐波对比，29次和31次的齿谐波明显减小。根据GB 755—2008中要求，端电压总谐波畸变量

(3)

式中,un—电机端子处n次谐波电压幅值与基波幅值之比；n—谐波次数；k=100。

根据式(3)，求得THD计算结果如表2所示。

表2 THD计算结果

3 对电机电磁参数与性能的影响

3.1 对气隙系数的影响

气隙系数Kδ表示由于齿槽存在而使气隙增大的倍数，由式(4)计算得出[4]

Kδ=Kδ1Kδ2

(4)

式中,Kδ1—转子有槽，定子虚拟为光滑时的气隙系数；Kδ2—定子有槽，转子虚拟为光滑时的气隙系数，Kδ1与Kδ2由式(5)计算得出。

(5)

式中，Bδm—气隙磁密最大值；Bδ—无槽时气隙磁密最大值。

通过二维场建立转子给定额定励磁时，定子无槽铁心如图5(a)；定子给定额定相电压且槽楔为非磁性槽楔时转子无槽铁心如图5(c)。图5(b)为定子无槽铁心时的气隙磁密曲线，图5(d)为转子无槽铁心时的气隙磁密曲线。

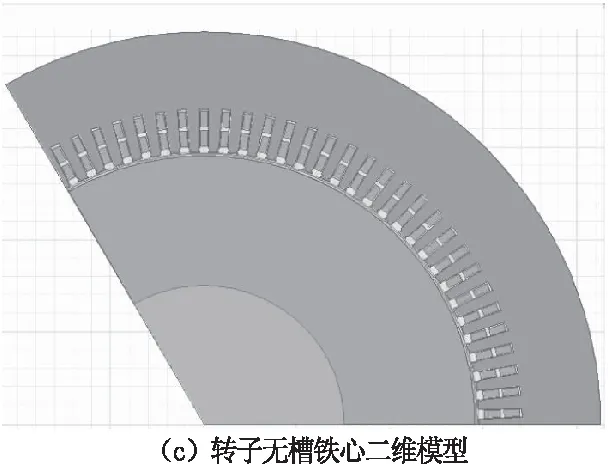
图5 定子无槽与转子无槽时二维模型气隙磁密分析

对于有磁性槽楔时转子无槽铁心的建模原理相似，在此不再重复，最后从气隙磁密曲线中测得Bδm和Bδ结果以及气隙系数的计算结果见表3。

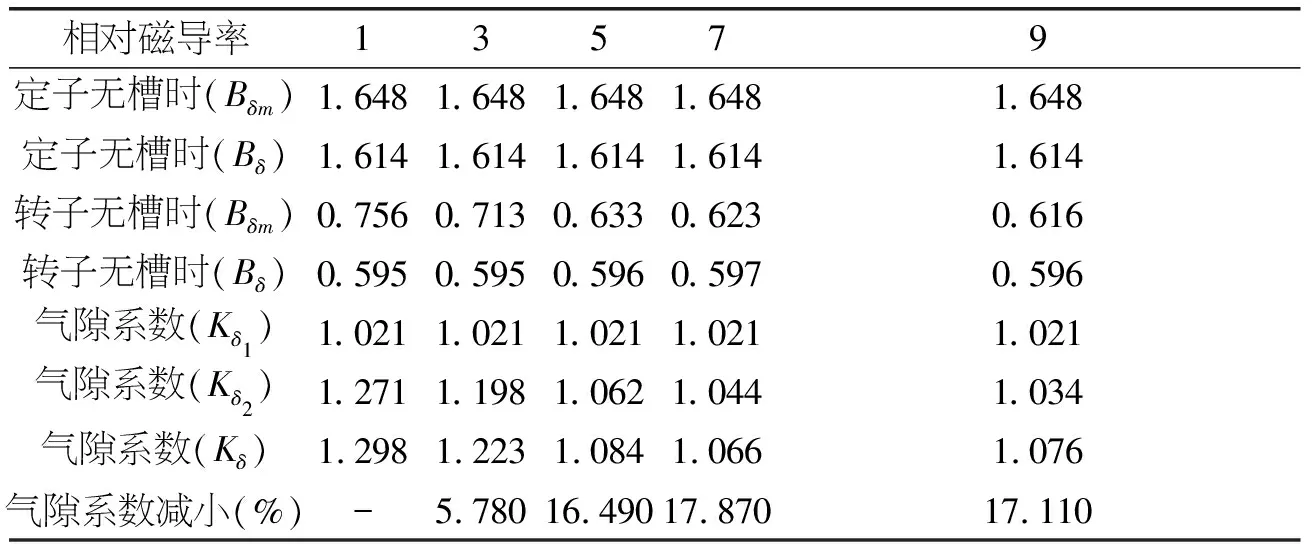
表3 气隙磁密幅值

从表3中可见选用磁性槽楔时，Kδ较非磁性槽楔都有相当程度的减小，同时也可以看出当槽楔相对磁导率为5之后气隙系数减小的比较小。

3.2 对励磁电流的影响

采用基于有限元理论的等效阻抗法对励磁电流进行计算。发电机空载运行时，负载端等效阻抗为无穷大(即开路)，在额定运行时每相的等效负载电阻Rφ和等效负载电感Lφ的值，计算如下

(6)

得出等效负载电阻Rφ=0.1024Ω，等效负载电感Lφ=0.2444mH。等效阻抗法的场路耦合电路图如图6所示。

图6 发电机额定运行外电路

在计算时，首先给定初始励磁电流值If(old)，通过计算得同步发电机端电压基波分量U，当U与额定相电压UφN之间的误差在允许范围内时，则可确定发电机的空载励磁电流If0，同理确定额定励磁电流IfN，如计算结果不满足收敛条件，则应调整励磁电流值，重新进行端电压U的计算。在迭代过程中，新的励磁电流为

if(new)=if(old)-β×(U-UφN)/UφN

(7)

由于发电机额定运行时每相的等效负载电阻和电感是按照式(7)求得的，所以当发电机的端电压满足收敛条件时，发电机定子电流与功率因数也同样满足收敛条件。最终采用不同相对磁导率磁性槽楔情况下的励磁电流如表4所示。

表4 不同相对磁导率对励磁电流的影响

由表4可知，随着磁性槽楔导磁性能的增强，电机空载励磁电流和额定励磁电流均明显减小。但相对磁导率为5之后励磁电流的减小比较小。

3.3 对短路比的影响

短路比Kc是同步发电机运行特性的一个重要参数，它是指产生空载额定电压所需的励磁电流Ifo与产生短路额定电流时所需励磁电流Ifk之比，即[5]

(8)

采用不同相对磁导率的磁性槽楔时，发电机短路比如表5所示。

表5 短路比计算结果

由表5可见，随着磁性槽楔相对磁导率的增大，短路比减小。因此，当负载变化时，由于阻抗压降较大，电机的电压变化率较大，发电机稳定性变差。所以由此看应选用相对磁导率较低的磁性槽楔。

4 磁性槽楔受电磁力分析

因为磁力线与槽楔表面基本全部垂直的，所以不存在Tx、Ty和T的切线分量。槽楔受力如图7所示。由于没有磁通通过槽内，所以Ty=0。由通过槽楔漏磁通引起的力Tx1和Tx2相当小，所以它们对槽楔的作用力可忽略[1]。

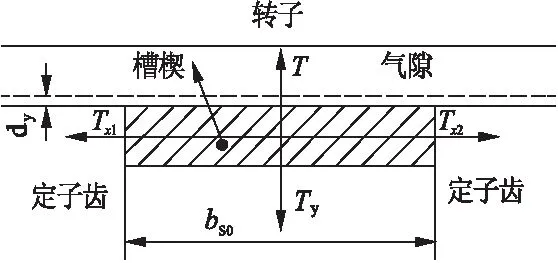
图7 槽楔受力示意图

结合文献[1]不同磁导率磁性槽楔单位长度上所受磁拉力Tm′为

(9)

磁性槽楔所受磁拉力随磁导率变化情况如图8所示。

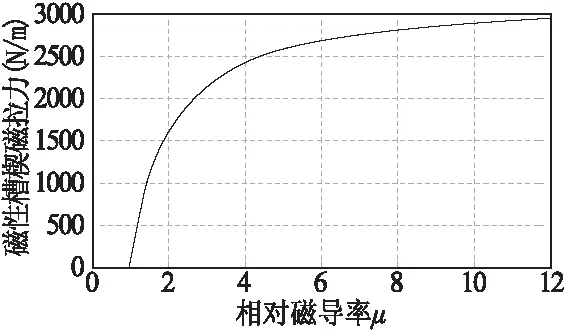
图8 槽楔磁拉力与槽楔相对磁导率关系

从图中可看出槽楔磁导率越大，所受的磁拉力也越大，同时随着槽楔磁导率μ的增大，槽楔受力接近于Tm′。可以看出选用磁导率越大的磁性槽楔，其所受磁拉力越大，所以在结合电机参数与性能的影响下在结合槽楔受力合理选用磁性槽楔。

5 结论

本文定量分析使用磁性槽楔对电机电磁参数和性能的影响，得出发电机在采用磁性槽楔后可减小电机气隙系数，改善气隙磁密波形，降低发电机输出电压畸变率。减小发电机励磁电流，节省励磁成本，但是同时增大了短路比，是短路能力有所下降。结合磁性槽楔相对磁导率从3到9的变化对发电机的参数与性能的影响以及磁性槽楔的电磁力分析，确定该电机选用相对磁导率为5的磁性槽楔最为合理。结合各个方面因素磁性槽楔的设计将朝向高磁导率、高电阻率和高强度材料的方向，以便进一步提高电机性能，降低电机损耗和温升，提高电机效率。

[1] 王绍禹. 磁性槽楔交流电机[M]. 北京: 水利电力出版社, 1987:24-28．

[2] 梁艳萍, 陈晶, 刘金鹏. 磁性槽楔对高压感应电动机电磁参数和性能的影响[J] . 电机与控制学报, 2010, 14(3):1-5.

[3] 汤蕴璆. 电机内的电磁场[M]. 北京: 科学出版社, 1998.

[4] 陈世坤. 电机设计[M]. 第2版. 北京: 机械工业出版社, 2000:50-56.

[5] 汤蕴璆, 史乃, 沈文豹. 电机理论与运行[M]. 第1版. 北京: 水利水电出版社, 1984:39-41.

[6] 何山. 磁性槽楔对大型永磁风力发电机性能的影响[J].电力设备, 2008, 9(5):53-56.