闭式冷却塔性能优化

朱月婷 涂淑平

( 上海海事大学，上海201306 )

本文从结构参数和运行参数两方面考虑，首先分析了结构参数和运行参数对冷却塔性能的影响，从中选取性能优化的变量，建立性能优化模型，并求解模型，分析各变量对冷却塔性能的影响，从中找出性能最优值。针对闭式冷却塔中蒸发冷却盘管，以盘管的换热面积作为目标函数，建立优化算法；通过性能参数的调整，一方面旨在降低盘管的设计换热面积，达到节省换热材料降低制造成本的目的；另一方面降低换热部件的压降，使用功率更小的风机和水泵，达到节电节水节能的目的。

1 结构因素的影响

(1)换热盘管管径对性能的影响

当管径变大时，在其它结构参数和运行参数不变的前提下，管径增大，导致空气掠过盘管表面的时间增加，使得喷淋水在塔体内的蒸发量增加，即蒸发冷却能力增强，传质系数提高；与此同时，由于管径变大，在循环冷却水量和盘管表面积不变的前提下，水的流速减小，使得流体湍流度降低，使盘管内水与管壁间的换热能力下降，换热系数减小。因此，在对盘管进行优化时，要同时考虑管径的变化分别对传热系数和传质系数的影响，使其在某一范围内达到最优值。

(2)换热盘管管间距对性能的影响

科学实验和生产实践证明，当盘管之间布置成正三角形、管间距是管外径的1.5～2倍时，可使喷淋水充分浸润盘管的外表面，使喷淋水覆盖面积达到最大，增大盘管的换热能力，同时也提高冷却塔的冷却能力。

2 运行因素的影响

(1)管内流速对性能的影响

在盘管截面积不变的前提下，管内工质流速变化就是管内流量的变化，在喷淋水密度、进塔空气量等参数不变时，流速的变化对冷却水至喷淋水膜之间的传热传质有着很大的影响。当流速增大时，一方面管内冷却流体与换热盘管间壁接触时间减少，导致不能充分换热；另一方面管内流速增大直接使得系统热负荷增加，在喷淋水密度、进塔空气量等参数不变时，直接会导致冷却塔出水温度下降。当流速减小时，管内工质湍流度降低，使盘管内水与管壁间的换热能力下降，直接导致换热能力降低。因此管内流速的增大或减少都将会影响管内冷却水的进出口温度，影响冷却幅宽。

(2)喷淋密度对性能的影响

当喷淋密度增加时，盘管外壁形成的水膜将完全浸润盘管外表面，并且在喷淋水一定压力的条件下，形成的水膜在盘管外表面以一定速度流动，这将使管内部热量的传递大大增加，冷却水出口温度下降，进出口水温差增大，强化了传热传质换热效果；然而，当喷淋水密度增加过多时，将会使盘管外表面的水膜形成一定厚度，水膜的厚度明显增加了热阻，影响管内热量向喷淋水和空气传递，因此喷淋水密度不宜过大，只要能够保证浸润盘管外表面所需最小喷淋密度即可。

(3)湿球温度对性能的影响

冷却塔中冷却水主要是依靠热传递、热对流、蒸发等形式将热量传给周围的空气。在设计和选择冷却塔时，湿球温度是最主要的气象参数。湿球温度代表在当地气温条件下，水可能被冷却的最低温度，即冷却塔出口水温的理论极限值。从理论上来说，冷却塔出口水温可以降到空气的湿球温度，这必须要求冷却塔的结构尺寸要无限大、空气与水充分接触的时间要无限长，再加上闭式冷却塔是属于间壁式换热，冷却效果并没有开式冷却塔好，这显然是不可能的。通过实验测得数据表明，闭式冷却塔出口水温一般比空气湿球温度高3～5℃。在冷却塔的结构尺寸及系统热负荷一定的条件下，随着入口空气湿球温度的升高，冷却水出口温度升高，冷却塔的冷却能力下降；反之，随着入口空气湿球温度下降，冷却水出口温度降低，冷却幅宽增加，冷却能力增强。

(4)气水比对性能的影响

气水比是指进塔空气进风量与喷淋水密度之间的比值，因只涉及两个因素，采取控制变量法，主要考虑当喷淋密度不变时，空气进风量变化对冷却水出口水温的影响；当空气进风量不变时，喷淋密度对冷却水出口水温的影响。

3 优化模型的建立

根据逆流闭式冷却塔传热传质理论，建立闭式冷却塔的数学模型。首先建立如下假设[1]：

(1)传热传质过程是一个稳态过程；

(2)冷却塔向周围环境的辐射散热忽略不计；

(3)喷淋水流量足够大，忽略喷淋水膜蒸发带来的影响；

(4)刘易斯数等于1；

(5)忽略空气-水膜接触面的热阻，因此接触面的空气焓值是与水膜温度相对应的饱和空气的焓值。

取微元控制体内三种流体的能量守恒关系式为：

dQ+dQa=0

冷却流体损失的热量dQ为：

Q=cpqmpdtp=-K(tpi-tw)dA

(1)

基于Merkel方程，焓差为传热传质的推动力，故空气得到的热量dQa为：

dQa=madia=hd(imasw-ia)dAa

(2)

假定一个恒定的水膜温度，对式(1)进行积分，得盘管的换热面积A为：

(3)

式中：cp—管内流体的定压比热容，J/(kg·℃)；qmp—管内流体的质量流量，kg/s；tpi，tpo—管内流体的进出口温度，℃；tw—喷淋水温度，℃；K—综合传热系数。

(4)

式中：αi—管内流体与管内表面之间的对流传热系数，W/(m2·s·℃)；di，do—分别为管内、外径，m；δ—传热管的厚度，m；ri，ro—分别为管内、外壁上污垢热阻，m2·s·℃/J；λ—管材传热系数，W/(m·K)；dm—传热管的对数平均直径，m；αo—管外喷淋水与管外表面之间的对流传热系数，W/(m2·s·℃)；

对于圆管，管内工质对流换热系数根据Dittus-Boelter公式得到：

(5)

采用流体平均温度作为定性温度，取管内径di为特征长度，上式实验证范围是：

Ref=(104，1.2×105),Prf

=(0.7，120),L/d<60

喷淋水与管外表面之间的对流传热系数非常多，根据Paker和Treybal在假设饱和湿空气的焓值与空气-水膜界面温度呈线性关系，给出了外径19mm错排管束的传热质经验公式[2]。管外喷淋水与管外表面之间的对流换热系数αo为：

(6)

式中：tw—喷淋水温度，℃；Г—喷淋密度，kg/(m·s)。

同样，对式(2)进行积分，得空气与喷淋水水膜表面的接触面积Aa为：

(7)

式中：qma—空气的质量流量，kg/s；hd—空气与水膜间的传质系数；imasw—水膜温度对应下的饱和空气焓值，J/kg；imai，imao—空气的进出口焓值，J/kg。

(8)

式中：Ga—单位面积的空气质量流量，kg/(m2·s)。

闭式冷却塔中的压降主要分为空气外掠管束压降dp和管程压降dpt，根据Niitsu的经验式[3]：

(9)

(10)

式中：nr—管排数；s2—纵向管间距，m；A—换热盘管的面积，m2；qma—空气的质量流量，kg/s；ρp—管内工质流体密度，kg/m3；νp—管内工质的流速，m/s；fi—管内摩擦压降摩擦系数；L—管长，m；C—管程数。

4 优化模型的求解

以某公司一闭式冷却塔为例，阐述优化模型的一般求解步骤。该冷却塔采用外径19mm，壁厚0.4mm的紫铜换热盘管，单组换热器是56片，一片有6层盘管，经过计算可知，盘管内径18.2mm，横向管间距是43.5mm，纵向管间距是77.2mm，单片换热盘管长度是20m。

设计参数为：qmp=120m3/h，tpi=37℃，tpo=32℃，tai=34℃，twb=28℃，PA=10130Pa，ΔP=100kPa；结构参数为：di=18.2mm，do=19mm，s1=43.5mm，s2=77.2mm，δ=0.4mm，L=20m，nr=56；运行参数为：vp=0.8m/s，Γ=0.05kg/(m·s)，qair=200m3/(kW·h)；换热盘管内热阻ri=0.0002m2·℃/W，换热盘管外热阻ro=0.0004m2·℃/W；紫铜的导热系数λ=65 W/m2·℃。

在进出口冷却水平均温度34.5℃时，查得水的导热系数λf=0.626W/(m·K)

假设喷淋水温度为31℃

=2.095×103W/(m2·K)

故

=884W/(m2·K)

由进出口冷却水温及喷淋水温可查得相应的焓值，代入公式，得：

此时A和Aa数值相差较大，应改变喷淋水温度，重新代入公式进行计算，直至两者面积达到最优值。经过反复计算，得：

A≈Aa=236.99m2

此时将盘管换热面积代入压降公式，得空气外掠管束压降：

管程压降为：

5 优化算法

根据上述模型，设计MATLAB计算程序，通过控制变量法，分别分析工质流速、喷淋密度、空气进风量对盘管换热面积和压降损失的影响，从而找到运行参数的最优值。优化程序算法流程图如图1所示[6]。

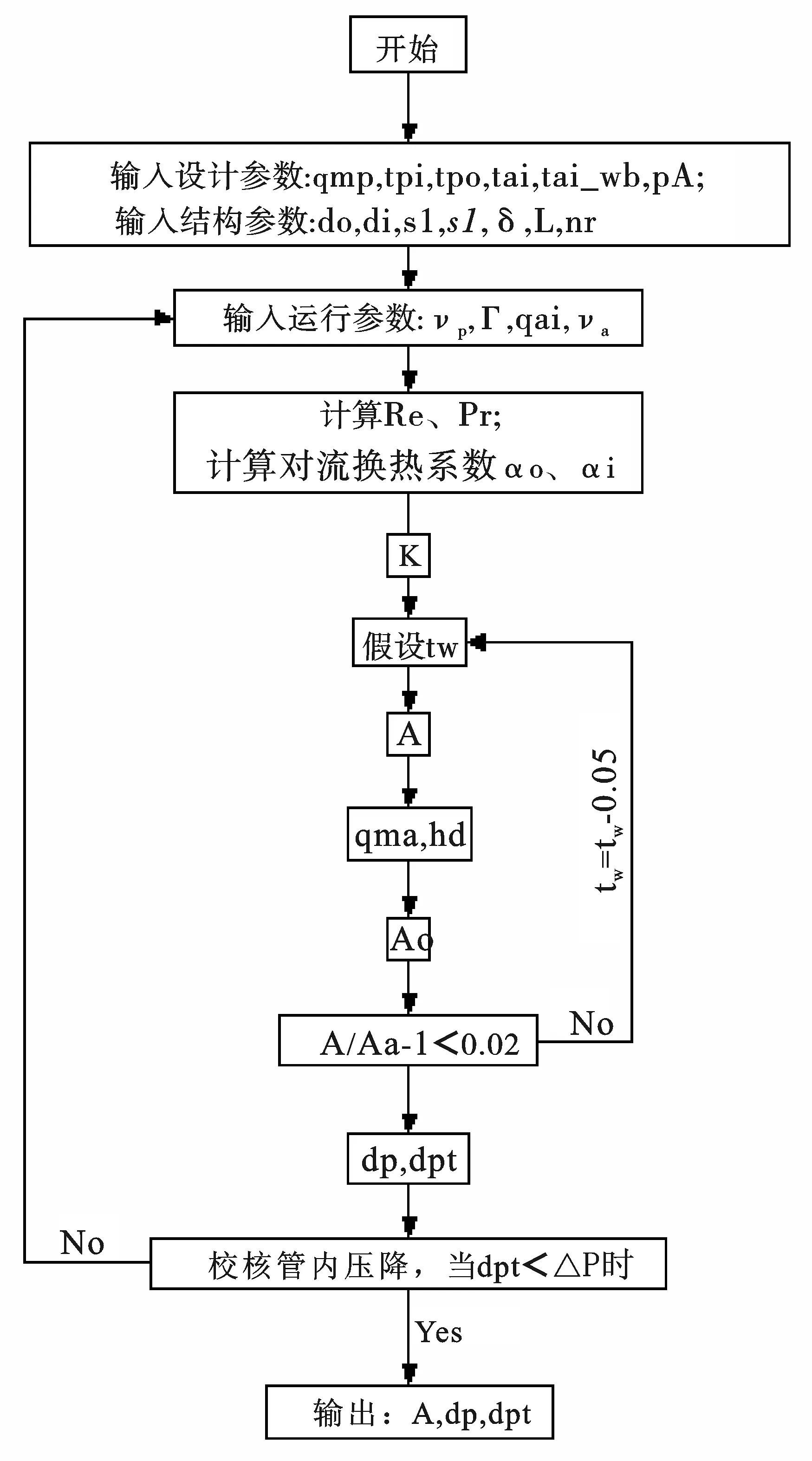
图1 优化程序算法流程图

输入设计参数、结构参数，选定运行参数，计算出雷诺数Re和普朗特数Pr，根据式(5)和(6)算出管内工质和水膜的对流换热系数，进而由式(4)算出综合传热系数。假设喷淋水水膜温度进行迭代运算，由式(3)计算出盘管换热面积A；再由A、式(8)和式(9)算出空气与水膜的接触面积Aa，当两者误差小于2%时结束循环，根据式(10)和(11)算出管束压降和空气外掠管束压降值，校核管内压降是否满足设计值，若满足，则输出A、dp、dpt；若不满足，改变运行参数值，重新迭代运算[5]。

6 优化结果分析

6.1 工质流速优化

控制喷淋密度Γ=0.05kg/(m·s)、空气进风量qair=200m3/(kW·h)不变，vp取0.8～1.6m/s范围。

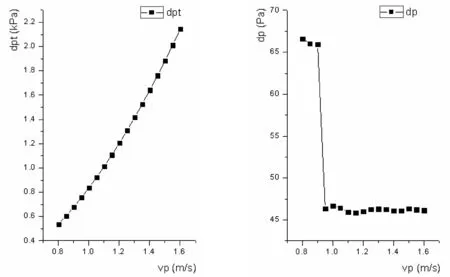
图2 管内工质流速对压降的影响

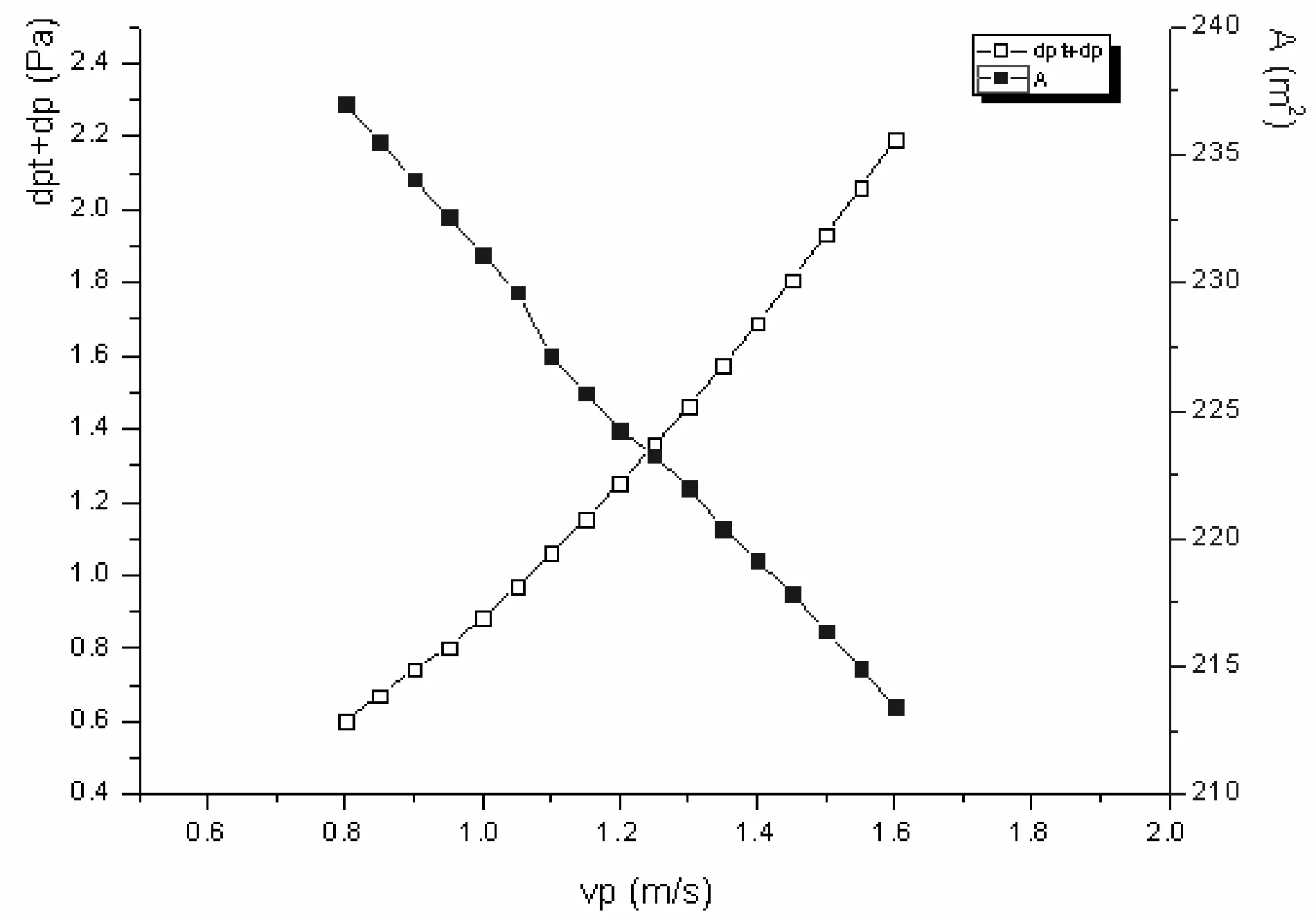
图3 管内工质流速对总压降和换热面积的影响

由图2可知，管程压降与工质流速近似成二次函数递增关系变化，这是由于在管程压降dpt的表达式中，dpt约为vp的二次函数；由图可知，在一定流速变化范围内，空气外掠管束压降dp基本保持不变，只是在vp=0.92m/s时，dp突然变小，这是由于工质流速的增长，盘管管程数减少的原因。

考虑流速变化对管程压降和空气外掠管束综合作用及换热面积的影响，如图3所示，随着vp的增长，A越来越小，dpt+dp越来越大，这是因为vp正比于雷诺数Re,Re正比于综合换数系数K，而K反比于A。因此为满足以更小的A获得较大的K值，所以取两曲线的交点，即取1.25m/s为最优。

6.2 喷淋密度优化

控制vp=0.125m/s、空气进风量qair=200m3/(kW·h)不变，喷淋密度Γ在0.05～0.5 kg/(m·s)范围内变化。

由图4可知，喷淋密度Γ对管程压降dpt几乎没有影响，只是Γ≈0.1 kg/(m·s)时，dpt减小，这是由于管程数减小的原因；由图5可知，空气外掠盘管压长dp随着喷淋密度Γ的增加而增加，这是由于dp表达式中与喷淋密度Γ成正比关系。由图可知，随着Γ的增加，换热面积A减小，dp增大，为使得压降不大时，取得较小的换热面积，故取两曲线交点，即喷淋密度Γ为0.15 kg/(m·s)时最优。

6.3 空气进风量优化

控制vp=0.125m/s、喷淋密度Γ=0.15 kg/(m·s)不变，空气进风量qair在200～1000 m3/(kW·h)范围内变化。由管程压降公式可知，dpt不是空气进风量qair的函数，所以空气进风量变化过程中，dpt一直保持不变。

由图6可知，随着空气进风量qair的增大，空气外掠管束的压降增加，盘管的换热面积A却减小，这是因为dp正比于空气质量流量qma，且qma正比于qair；换热面积A与qair成反比。为使得压降不大时，取得较小的换热面积，故取两曲线交点，即空气进风量qair为600m3/(kW·h)时最优。

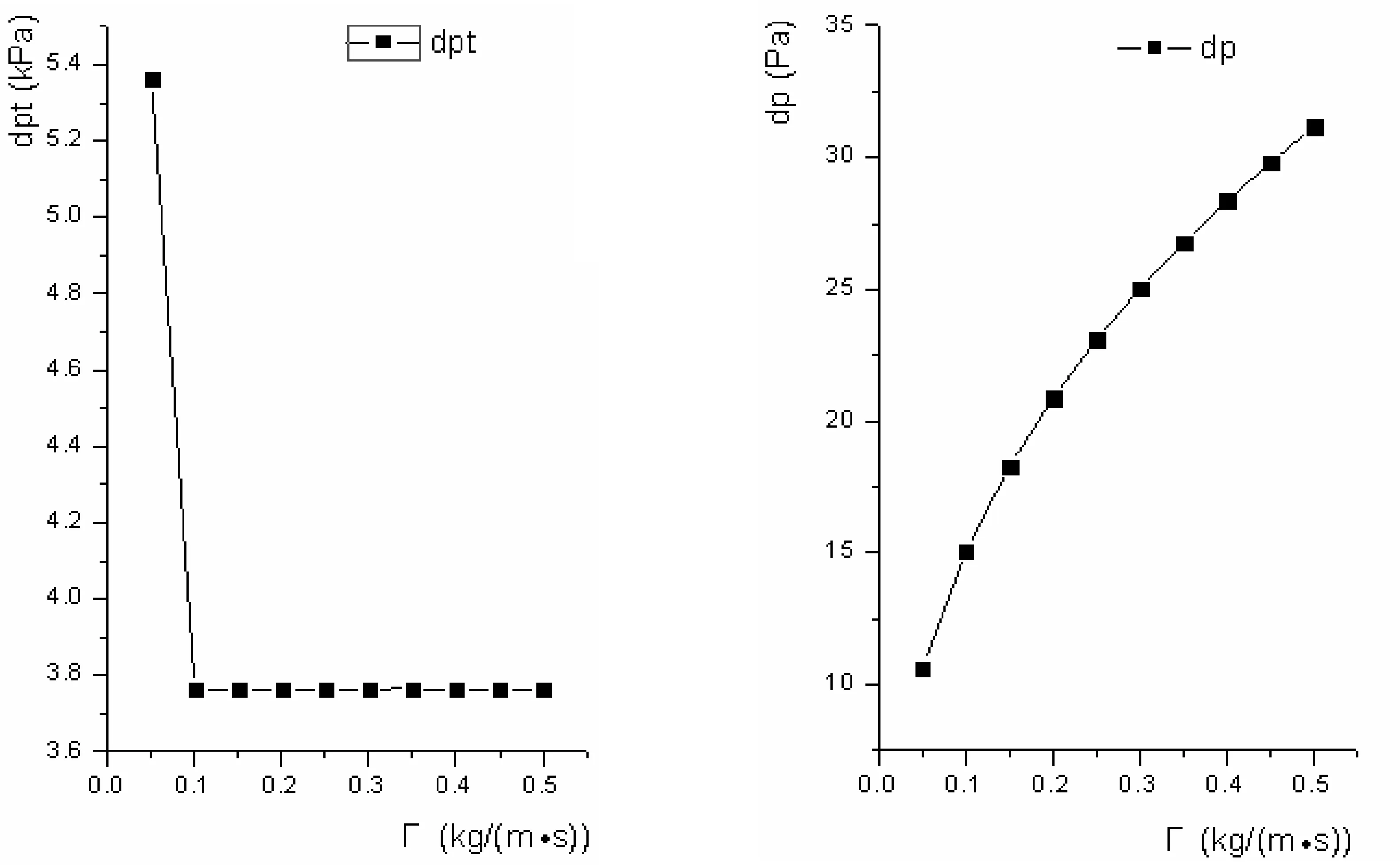
图4 喷淋密度对压降的影响

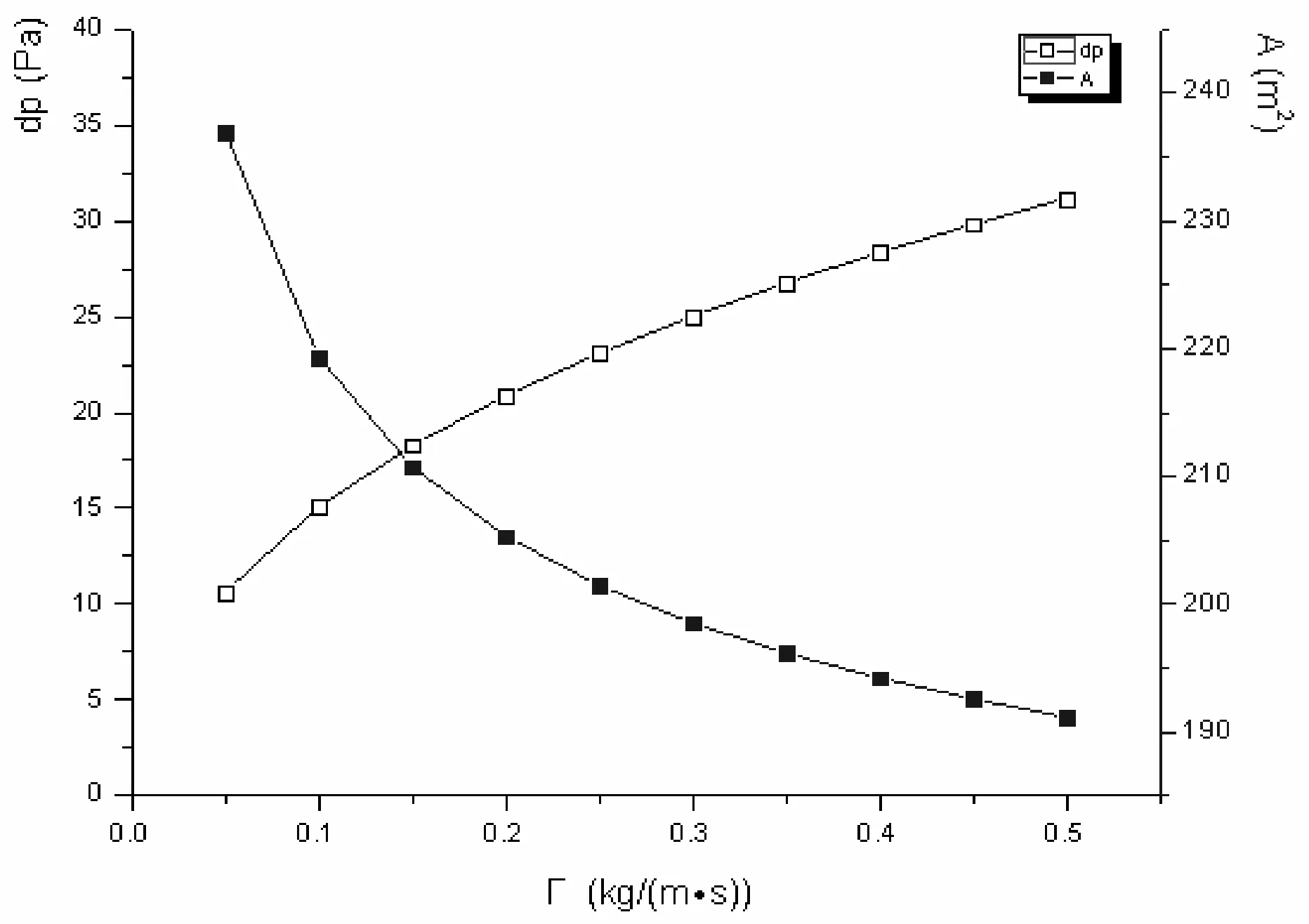
图5 喷淋密度对空气外掠管束压降和换热面积的影响

图6 空气进风量对空气外掠管束压降和换热面积的影响

[1] 段光明.管式蒸发冷却器的传热传质和结构优化[D].上海:同济大学，1992

[2] 薛覆中. 工程最优化技术[M].天津：天津大学出版社，1998

[3] 杨建坤，张旭，刘乃玲 .板式间接蒸发冷却器的优化设计[J].制冷空调与电力机械，2004(5):43-46

[4] J.R.Khan，B.A.Qureshi，S.M.Zubair，A comprehensive design and performance evaluation study of counter flow wet cooling towers,International Journal of Refrigeration 2004,27,914923

[5] 朱冬生，涂爱民，李元希，等，蒸发式冷却器的应用前景及其设计计算.中国制冷学会2007学术年会论文集，2007:249-253

[6] 朱冬生，沈家龙，蒋翔，等.蒸发式冷凝器管水膜传热性能实验研究[J].高校化学工程学报，2007,21，(1)：35-40

[7] 吴佳菲，曾力丁，郑伟业，等.高效闭式冷却塔的优化设计及节能运行[J].化学工程，2012，40(6):23-26