面向起飞质量的小型飞航导弹参数优化方法

陈阳阳，陈卫东，吴限德

(1.哈尔滨工程大学航天与建筑工程学院，黑龙江 哈尔滨150001;2.北京电子工程总体研究所，北京100854)

近年局部冲突频发，对固定目标和低速运动目标的精确打击需求激增，该背景下近程小型飞航导弹以其成本低廉、打击精度高、研制周期短、效费比突出、作战反应时间短、反导系统对其拦截效果差等优点成为各国竞相研制和装备的导弹类型［1-3］。

小型飞航导弹打击效果受雷达反射面大小、飞行速度、飞行高度、制导方式和机动性等因素的影响，而导弹的总体质量、气动布局、结构形式和弹道形式直接决定了速度、高度、机动性和隐身性等指标。因此，在气动布局、结构形式和弹道形式确定的前提下，有必要研究导弹起飞质量的优化方法，确定起飞质量对导弹其他总体参数的影响，兼顾射程、巡航高度、巡航速度、法向过载、发射角、发动机装药和末速度等因素，最大限度降低导弹起飞质量，进而降低导弹对发射装置和运输环节的要求、提高导弹性能和效费比等。

导弹总体参数优化多采用纵向平面运动的质点弹道模型，根据研究背景的不同选取不同的优化模型，国内外文献［4-6］中的目标函数包括综合目标、最远射程、最小总加热量、杀伤概率、时间最短等;设计变量通常选取程序角的控制参数、动力系统(推力的变化、燃料质量、发动机点火时刻)等;约束条件通常为过载限制、速度限制、攻角限制、高度限制、气动热限制、特殊点参数限制(助推结束时速度限制、转弯时刻攻角限制、落地条件等);优化方法通常有粒子群算法、复合形法、序列二次规划法、遗传算法、混合优化算法等。这些文献中多进行弹道控制参数的优化，对导弹总体参数的优化涉及不多，尤其是以起飞质量为直接目标，以射程、速度和过载等为约束条件的优化研究较少。

文献［7-8］从动力系统出发估算了导弹的起飞质量，但对总体参数的选取并没有进行深入的研究。本文以纵向平面运动的方案弹道为模型，推导了起飞质量公式，并利用复合形法以最小起飞质量为目标，通过具体算例，对飞航导弹的总体参数进行了优化。

1 弹道模型

导弹的总体参数确定是研制初期的关键问题，贯穿导弹研制全过程，是其他参数确定的主要依据，总体参数(起飞质量m0，发动机的推力F，弹翼面积S)依据导弹的战术指标和飞行性能(导弹的射程d、飞行高度H及导弹的飞行速度V)来初步确定，在发动机推力F及弹翼面积S确定之后，起飞质量m0则成为导弹初步研究的重点。影响起飞质量的因素主要有:结构参数、动力系数参数、有效载荷质量、气动参数、弹道特性、最大射程等，这些因素在减小导弹质量过程中存在耦合，给定量分析导弹的起飞质量带来难度。

本文所作优化研究基于弹道计算模型，研究过程中考虑了飞行过程中的诸多要素。导弹在空间的运动情况十分复杂，为了提高弹道优化的效率，本文将导弹简化成可控质点，只考虑纵向平面内的运动，导弹数学模型［9］如下:

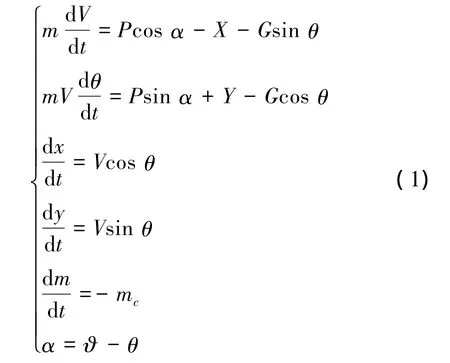
式中:m为导弹瞬时质量，V为速度，P为推力，G为重力，X为气动阻力，Y为气动升力，α为攻角，θ为弹道角，ϑ为俯仰角。

给定式(1)中各参数的初始数据，利用龙格-库塔法求解上式即可得到导弹在给定控制规律(导弹俯仰角随时间变化关系)下的飞行弹道。

2 优化模型

本文采用复合形法对小型飞航导弹起飞质量和其他总体参数进行优化，优化模型首先给出优化目标函数的具体推导过程，然后确定优化的设计变量和约束条件，最后对优化方法和优化过程进行了详尽的阐述。

2.1 目标函数

本文以最小起飞质量作为优化的目标函数，下面对起飞质量进行详细的推导。

起飞质量表达为

式中:m0为导弹起飞质量，m1为导弹第一级质量，本文中为助推级质量，m2为导弹第二级质量，本文中为导弹主级质量。将式(2)具体到各分系统质量:

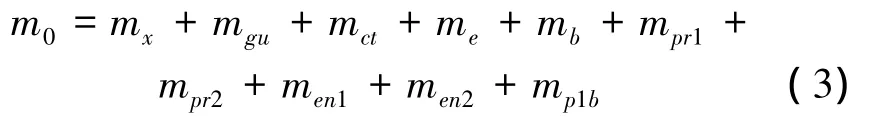
式中:mx为战斗部装药质量，mgu为导引头质量，mct为飞控系统质量，me为电气系统质量，mb为弹体质量，mpr1为助推发动机装药质量，mpr2为巡航发动机装药质量，men1为助推发动机结构质量，men2为巡航发动机结构质量，mp1b为助推发动机结构质量。其中，mgu、mct、me为确定值，mpr1、mpr2为设计变量，本文所取发动机为固体火箭发动机，men1的统计值一般可取men1=0.8mpr1，men2的统计值为men2=0.6mpr2，mp1b包括助推器的弹翼、蒙皮等结构质量，其值为mp1b=0.1mpr1。

mb包括弹身质量、弹翼质量和舵面及其操纵机构，弹身结构质量不包括推进剂的贮箱质量或发动机燃烧室的壳体质量，在初步设计阶段，通常取型号的统计值，飞航导弹通常取 (0.09～0.15)m2，本文取 0.12m2，弹翼结构质量为 (qw/p0)m2，其中p0为翼载，其值为p0=m2/S，S为弹翼面积，qw为单位面积弹翼的结构质量，它与弹翼的结构形式、材料类别、工艺方法及要求承受的最大载荷等因素有关，对于小型导弹可取12+0.018p0，即弹翼质量为12S+0.018m2，若导弹弹翼采用“×”形布局，则弹翼结构质量为上式的2倍，舵面及其操纵机构质量为舵面结构质量和操纵机构质量之和，在初步设计阶段，可根据统计数据估算，对于飞航导弹，舵面结构质量通常取 (0.004～0.04)m2，本文取 0.02m2，操纵机构质量通常取0.01+0.7×10-4τ(τ为操纵机构的工作时间)，本文取0.019m2，则舵面及其操纵机构质量为0.039m2，以上几部分相加则得到弹体结构质量。

综合以上分析，导弹起飞质量计算公式如下

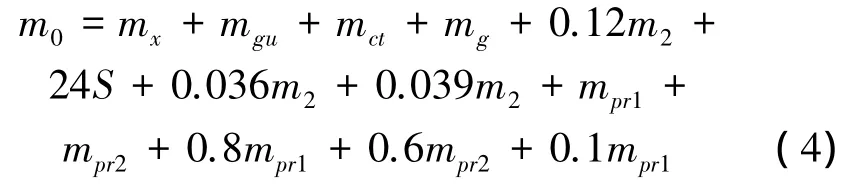
其中

将式(5)代入式(4)可得

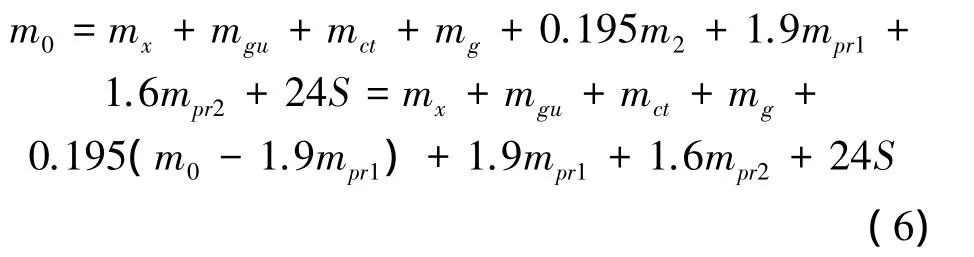
将式(6)等式变换:

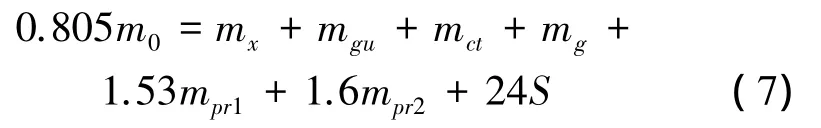
最后得到起飞质量的计算公式:

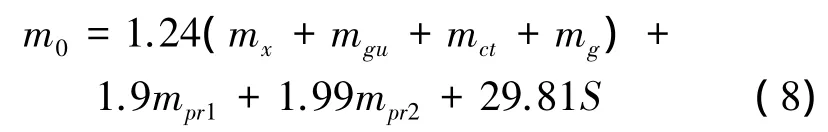
2.2 设计变量

在弹体结构形式及结构质量确定的情况下，起飞质量与助推器推进剂质量mpr1、巡航发动机推进剂质量mpr2有关，同时，本文从弹道计算出发，研究中必须考虑到导弹飞行过程中诸多要素(速度、射程、过载等)的限制，初始发射角决定了导弹的助推结束的高度和速度，巡航高度对导弹的射程和末速度均有影响，助推和巡航发动机的性能对弹道特性影响较大，故设计变量选取为

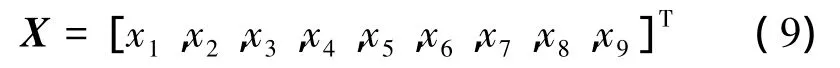
式中:x1为助推器推进剂质量，x2为巡航发动机推进剂质量，x3为巡航高度，x4为导弹初始发射角，x5为助推发动机推进剂比冲，x6为助推发动机推力，x7为巡航发动机推进剂比冲，x8为巡航发动机推力，x9为发射轨道长度。

2.3 约束条件

总体参数不仅要满足战术技术指标的要求，同时还要满足飞行过程中受到的各种外在因素的限制，综合考虑，约束条件选取为

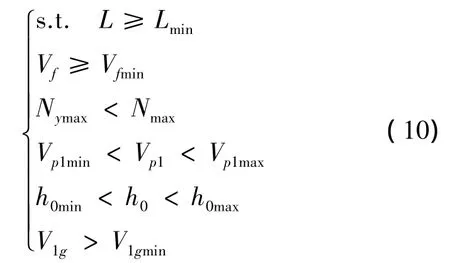
式中:L为导弹射程，Vf为导弹末速度，Nymax为导弹最大法向过载，Vp1为导弹最大速度，h0为巡航高度，Vlg为导弹离轨速度。其中

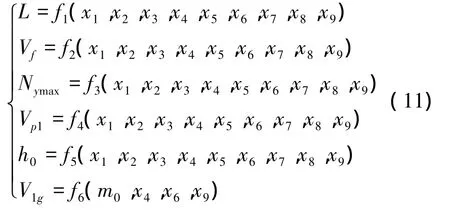
从上式可以看出，约束条件为设计变量的隐式函数，无法得到确切的表达形式，其值只能通过求解弹道方程得到。

2.4 总体参数优化方法

导弹总体参数优化涉及变量多、计算量大，目前用于总体参数优化的方法包括遗传算法、序列二次规划法［10］、改进粒子群算法等，以上算法理论性强，发展前景广阔，理论研究价值较高，但作为工程应用，需要算法的可靠性高、实用性强，复合形法［11］是单纯形法对约束优化问题的推广，算法简单、提出较早，理论发展成熟。复合形法的优点是不需要目标和约束函数的任何导数信息，始终在可行域内寻优，有一定收敛精度，能有效处理不等式约束的优化问题，而且是在可行区进行较广泛的搜索，求出的最优解通常是全局最优解。

本文研究的导弹总体参数优化问题，目标和约束函数的导数无法求解，采用复合形法可以得到满意的优化结果，通过将复合形法与弹道计算程序结合起来，实现总体参数的优化，图1是优化流程图。

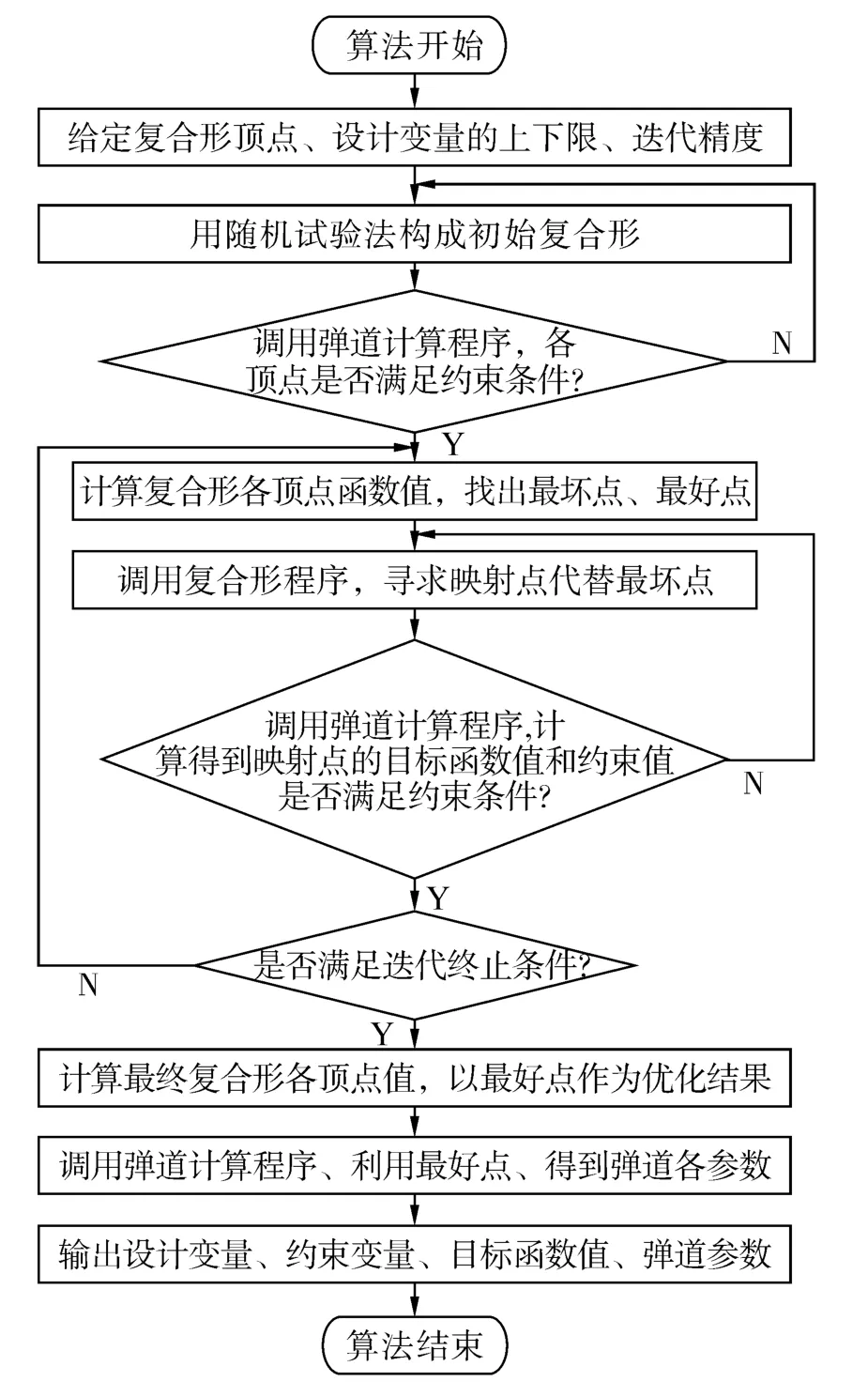
图1 优化流程图Fig.1 Optimization flow chart

为提高计算的收敛速度和保证计算的精度，可采用设计变量归一化处理，使设计变量值在同一数量级内变化。

3 最小起飞质量优化算例

本文仿真算例的战术技术指标包括:射程不小于48 km，末速度不小于150 m/s，巡航速度Ma为0.8左右，导弹离轨速度不小于30 m/s。导弹气动布局为正常式，弹翼为梯形翼，采用“×”型布局，弹体几何参数详细数据见表1。

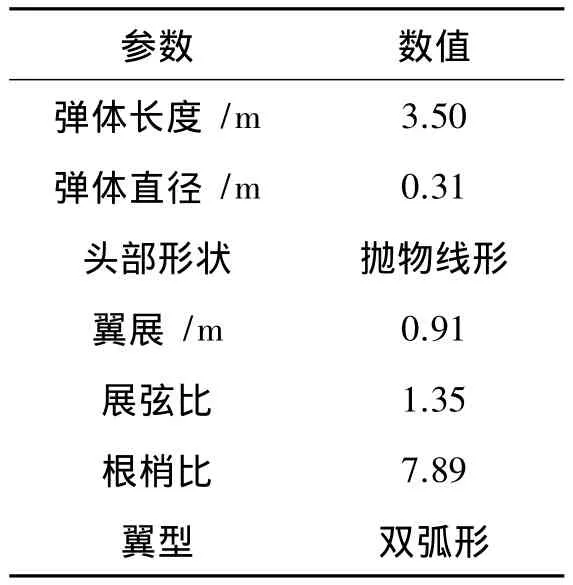
表1 弹体几何参数Table 1 Missile body geometric parameter

气动数据计算采用工程计算方法，具体计算方法参见文献［12-14］。方案弹道形式为:初始段无控飞行，导弹达到最高点之后转弯，当高度降低到距离巡航高度一定值时，导弹平滑过渡到巡航高度，巡航发动机开始工作，然后按预定高度飞行。优化初始质量 366.99 kg。

本文优化方程可表达如下

程序开始，在可行域内，给定设计变量的一组初始值，利用这组值求得复合形其余顶点值，构成初始复合形。从初始复合形出发，利用映射点取代最坏点，构成新的复合形，不断迭代，当复合形各顶点值误差小于误差限时，可认为优化过程结束。图2、3是设计变量和目标函数不断迭代变化的过程，其中设计变量x1～x4为迭代寻优得到的参数，x5～x9为经过优选确定的参数。

从图2中可以看出，设计变量经过58次迭代最终均趋于稳定值，其值为归一化处理结果，表2列出了各设计变量的优化结果。

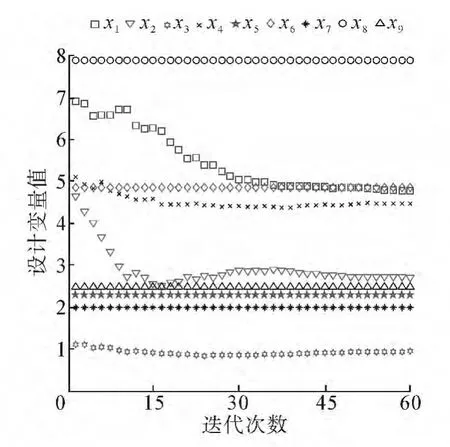
图2 设计变量优化过程Fig.2 Design variables optimization procedure

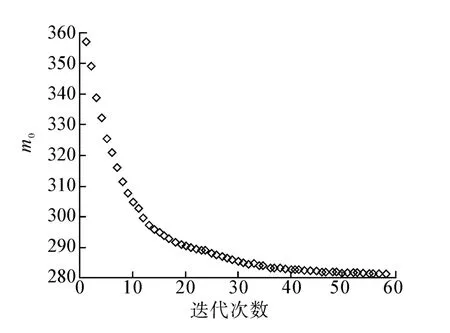
图3 目标函数优化过程Fig.3 Goal function optimization procedure

表2 设计变量优化结果Table 2 Design variables optimization result

与表2相对应，表3给出了总体参数优化结果，包括助推器推进剂质量、巡航发动机推进剂质量、巡航高度、导弹发射角、助推发动机推进剂比冲、助推发动机推力、巡航发动机推进剂比冲、巡航发动机推力和发射导轨长度等参数。

将上述优化结果代入弹道计算程序中，得到弹道优化结果，目标函数值及约束条件参数值如表4所示。

从表3可以看出，采用优化之后的弹道参数满足各种约束的限制，同时起飞质量较原先方案有明显减小，在满足各种约束的前提下，起飞质量减小了20.80%，优化效果显著。本文优化方法基于弹道计算，图4列出了弹道形式、速度曲线、攻角变化曲线和法向过载曲线。

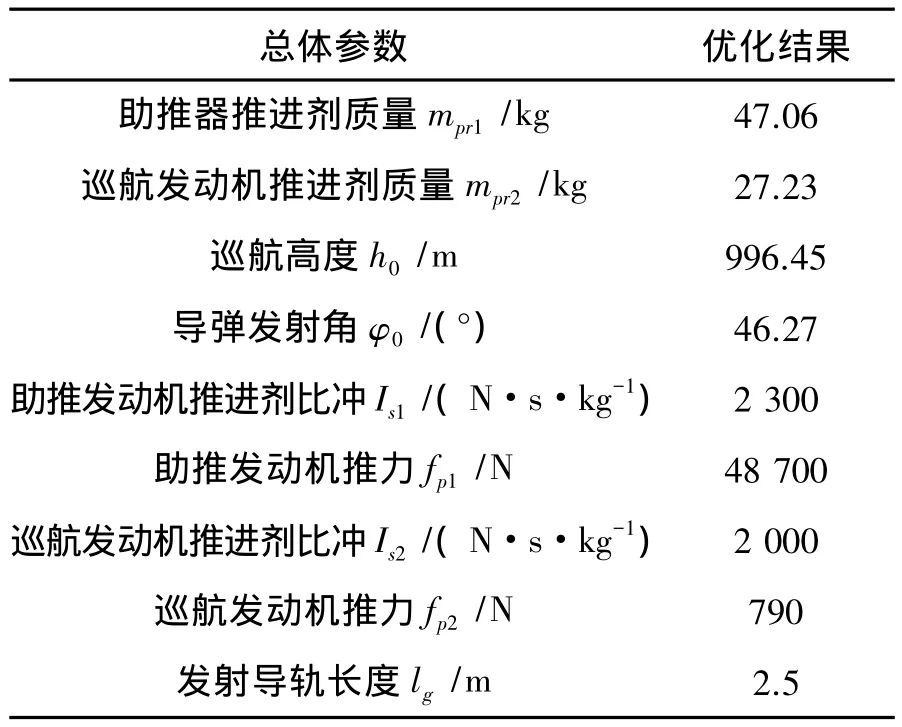
表3 总体参数优化结果Table 3 Design variables optimization result

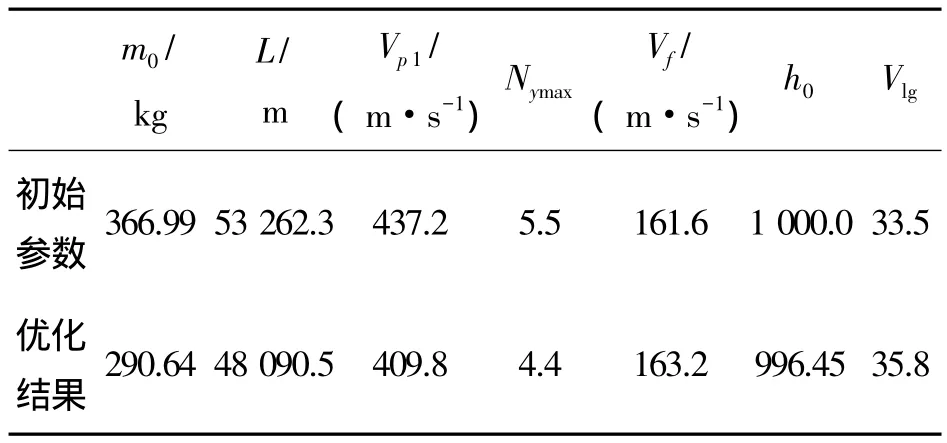
表4 目标函数值及约束条件参数值Table 4 Goal function value and constraint condition parameters

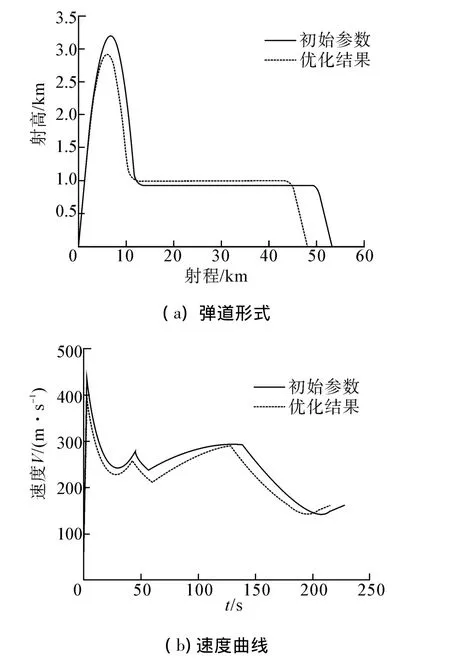
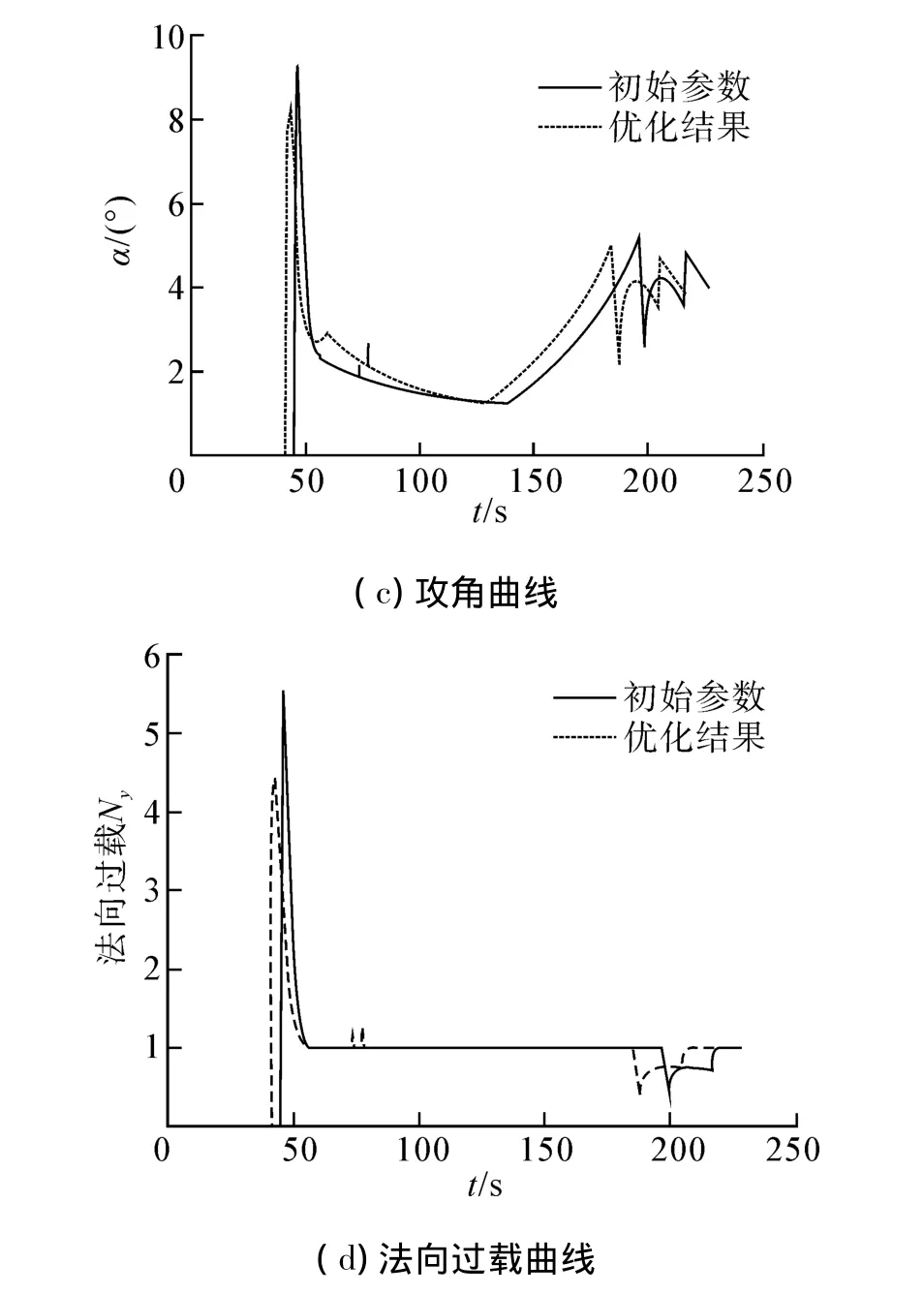
图4 仿真结果曲线Fig.4 Curves of the simulation results

图4给出了初始参数和优化结果计算的弹道参数对比曲线。从图中可以看出，由于初始值是可行域内的一组值，所以初始值和优化结果的弹道特性均满足优化的各种约束条件。优化结果的射程小于初值的射程(图4(a))，但是通过优化之后，起飞质量得到大幅减小;优化结果的速度略小于初值的速度(图4(b))，较小的巡航速度在一定程度上减小了导弹在飞行过程中的能量损失;优化之后，飞行过程中的最大攻角减小，攻角变化较初值变平缓(图4(c))，有利于提高导弹在飞行中的稳定性;优化结果的最大法向过载小于初值的最大法向过载(图4(d))，减小了对弹体结构和弹内仪器的设计压力。

4 结束语

本文设计和推到了面向起飞质量的小型飞航导弹参数优化模型，优选了设计变量和优化目标函数;以小型飞航导弹初步设计变量为输入，进行了优化算法的工程应用，最后确定助推器推进剂质量、巡航发动机推进剂质量、巡航高度和导弹发射角等总体参数。通过仿真结果看出，导弹在满足战术技术指标的前提下，起飞质量最小。采用本文方法能够有效地解决小型导弹总体参数优化设计问题，为工程应用提供参考。

［1］杨林冲，陈勇.小型精确制导武器关键技术及发展现状分析［J］.飞航导弹，2010，11:11-14.

［2］HEWSON R.Small but perfectly formed mini munitions offer precision impact［J］.Jane’s International Defense Review，2009(9):72-77.

［3］TITTLE R.New weapons for a new era—UAS weapons get smaller［J］.Unmanned Systems，2009(7):29-31.

［4］郑月英，刘辉，李俊峰.滑翔弹道优化设计研究［J］.宇航学报，2009，30(3):858-862.ZHENG Yueying，LIU Hui，LI Junfeng.Spacecraft gliding trajectory optimization［J］.Journal of Astronautics，2009，30(3):858-862.

［5］HITOSHI M，JASON C H.Minimum-fuel trajectory along entire flight profile for a hypersonic vehicle with constraint，AIAA，98-4122［R］.American Institute of Aeronautics and Astronautics，Inc.，1998:212-224.

［6］刘恒军，姜欢，陈万春.防空导弹动能杀伤多层弹道优化MDO算法应用［J］.北京航空航天大学学报，2010，36(2):145-149.LIU Hengjun，JIANG Huan，CHEN Wanchun.Application of MDO algorithm to multi-tier trajectory optimization design for a surface-to-air missile kinetic kill［J］.Journal of Beijing University of Aeronautics and Astronautics，2010，36(2):145-149.

［7］于剑桥，刘莉，文仲辉.高速动能导弹起飞质量设计方法研究［J］.弹箭与制导学报，2003，23(4):101-108.YU Jianqiao，LIU Li，WEN Zhonghui.Method research on take-off mass design for hypersonic velocity kinetic energy missile［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2003，23(4):101-108.

［8］何博，聂万胜，丰松江.固体导弹最小起飞质量研究［J］.装备指挥技术学院学报，2007，18(6):45-49.HE Bo，NIE Wansheng，FENG Songjiang.Research on the minimal take-off mass of solid missile［J］.Journal of the A-cademy of Equipment Command＆ Technology，2007，18(6):45-49.

［9］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京:北京理工大学出版社，2003:66-98.QIAN Xingfang，LIN Ruixiong，ZHAO Yanan.Missile flight mechanics［M］.Beijing:Beijing Institute of Technology Press，2003:66-98.

［10］BRAIN C F.Some tools for the direct solution of optimal control problems［J］.Advance in Engineering Software，1998，29(1):45-61.

［11］陈卫东，蔡荫林，于诗源.工程优化方法［M］.哈尔滨:哈尔滨工程大学出版社，2006:234-238.CHEN Weidong，CAI Yinlin，YU Shiyuan.Engineering optimization method［M］.Harbin:Harbin Engineering U-niversity Press，2006:234-238.

［12］苗瑞生，居贤铭，吴甲生.导弹空气动力学［M］.北京:国防工业出版社，2006:364-546.MIAO Ruisheng，JU Xianming，WU Jiasheng.Missile aerodynamic［M］.Beijing:National Defence Industrial Press，2006:364-546.

［13］列别杰夫，契尔诺勃洛夫金.无人驾驶飞行器的飞行动力学［M］.张炳暄，译.北京:国防工业出版社，1964:116-351.

［14］钱翼稷.空气动力学［M］.北京:北京航空航天大学出版社，2004:23-107.QIAN Yiji.Aerodynamic［M］.Beijing:Beijing University of Aeronautics and Astronautics Press，2004:23-107.