陕北侏罗纪煤田榆神矿区中鸡勘查区煤层厚度混合分布特征及其意义

, ,,

(1.陕西省煤田地质局一八五队，陕西 榆林 719000； 2.中煤科工集团西安研究院，陕西 西安 710077； 3.中国地质大学(武汉)资源学院，湖北 武汉 430074； 4.中国地质大学地质过程与矿产资源国家重点实验室，湖北 武汉 430074)

0 引 言

现代矿床学研究表明，众多矿床的形成具有多来源、多阶段和多成因的特点 (翟裕生等,1996 )。故而可将形成一个矿床的过程看作是多个总体的混合或叠加，在数学上这种混合或叠加可以用混合总体筛分的数学模型来描述。研究勘查数据的混合分布特征可以帮助揭示多期次、多重叠加的地质作用与地质过程，是勘查数据统计分布特征研究的重要内容之一。为了深入研究地质体(如岩体、矿体)的成因或形成过程，需要从混合分布的样本数据中将各成分总体分离出来(或估计出来)，对成分总体的有关参数进行估计，这个过程称为混合分布的筛分。混合总体的筛分方法可分为3类：解析法(McLachlan et al,2000)、图解法(辛克莱,1976; 赵鹏大等,1983; 王琳,2005)、数值法。数值法是近年来的主流方法，它运用各种数学最优化理论方法(如最小二乘法、最大似然法等)进行混合总体的筛分。EM算法目前是数值法中发展最快的一种(刘向冲等,2011; 张锋，2012)。EM算法及其扩展算法如MML-EM算法等为勘查地球化学数据、金属矿床品位分析数据的混合分布筛分以及解释地质成因提供了一种快捷优良的定量化工具，然而在煤田地质中的应用还比较少见。

掌握煤层厚度变化规律，对于矿区煤炭资源估算及生产建设具有重要意义。前人对煤层厚度(简称“煤厚”)空间变化性总体上认为沉积环境控制煤厚区域变化，构造主要引起煤层厚度的局部变化(琚宜文等, 2002; 高荣斌等2011)。实际上煤厚往往呈现更加复杂多样的变化，它往往不是单一因素造成的，而常常是几种因素综合作用的结果，基底的沉降幅度和速度、沉积物的补给及植物遗体的堆积速度、成煤期后的构造活动对煤层厚度及其变化都具有一定影响(李恒堂等,1995)。在同一矿井中的不同煤层或同一煤层的不同部位，引起煤厚变化的原因也可能不同，有些地方以原生变化为主，而另一些地方则可能因后发生冲蚀或构造挤压引起。因此，煤厚变化通常是多种因素复合作用的结果，并且不同因素所起的作用还有着强弱上的差别，这些因素共同作用的信息可以体现在煤厚勘查数据中。因此，应用混合分布理论与方法来研究煤厚主要控制因素是可行的。

本研究以陕北侏罗纪煤田榆神矿区中鸡勘查区83个钻孔中测量所得的3个主要煤层(2-2(2-2上)煤、3-1煤、4-3煤)的煤厚数据为例，研究煤厚的混合分布特征，定量描述煤层的变化规律并进一步分析析混合分布中各子总体的地质意义。

1 有限混合分布模型和EM算法

1.1 有限混合分布模型

地质勘查数据的多总体性特点具有普遍性，在开展统计分析中不容忽视。有限混合模型提供了一种用简单分布拟合复杂分布的强劲灵活的概率分析数学工具。不失一般性，假定样本的概率密度模型为(McLachlan et al,2000)：

(1)

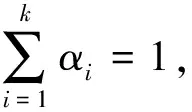
有限混合分布中，当模型分支数为1时，混合分布总体是单一分布，反映数据是同质的；当分支数多于1时，混合分布总体是多成分的，反映数据是异质的。混合分布总体通常可由多个单一分布以某种权重叠加来模拟，这些单一分布与某一类型的端元组分相联系，可能指示着某种内在的控制因素。因此，如何有效获取混合分布数据中的分布类型及其参数、分支个数、混合权重，既是有限混合分布模型研究的核心问题，也是地质勘查数据统计分布研究的重要内容。

高斯混合模型以其形式简单、计算方便等特点，受到普遍采用。尽管地质勘查数据统计大多具有非线性、非高斯特性，然而，相对于勘查地球化学微量元素数据而言，煤厚数据的非高斯特性通常表现不是很强烈。另外，混合高斯概率密度函数模型具有广泛适用性，原理在于：当样本足够大时，混合分布中各子分布渐进分布为正态分布，选择合适的模型参数，混合高斯概率密度可对任意形状概率密度函数进行精确拟合(柳贵东等,2011)。因此，可以简化研究的复杂度，采用高斯混合模型来开展本研究，即利用一定数量的正态分布概率密度函数，通过线性叠加混合来逼近煤厚变量的概率密度函数。在有限混合分布模型现有的参数估计方法中，基于极大似然估计原理的EM算法近年来最受关注。

1.2 EM算法

EM算法(Expectation-Maximization Algorithm，期望最大化算法)是一种从“不完全数据”中求解模型参数的极大似然估计的方法。它提供了一个高效的迭代算法用来计算这些数据的最大似然估计(张士峰，2004)。EM总体算法流程为：初始化分布参数，然后反复迭代直到满足收敛条件，终止迭代。EM算法的每一次迭代过程都分为2个步骤：(1) E步：估计未知参数的期望值，给出当前的参数估计；(2) M步：重新估计分布参数，以使得数据的似然性最大，给出未知变量的期望估计。当迭代结束，最终可求出使极大似然值最大的1组参数，此组参数即作为混合分布概率密度函数未知参数的极大似然估计解。

EM算法由Dempster等(1977)提出，现已成为混合模型拟合的主流方法，并出现了基于EM算法的多种变体方法。经典的EM算法解决了如何估计混合模型参数的难题，然而混合模型分支数量确定问题尚未得到彻底解决。目前最典型的方法是Figueiredo等(2002)提出的基于MML(Minimum Message Length Criterion，最小信息编码)准则和EM框架的算法，通常称为MML-EM算法。该算法将参数估计和模型选择紧密结合到同一处理流程中，能同时处理分支数和模型参数这2个问题，其算法思想为：在EM算法迭代过程的E步骤和M步骤之后增加L步骤，即利用前2步计算参数计算相应的信息长度，重复上述第3步，直到求出在信息长度最小条件下的最优分支数和分布参数。详细公式理论推导和算法实现见文献(Figueiredo et al, 2002)。此外，还有其他角度对EM算法进行改进，寻求最优分支数，如基于遗传算法的GA-EM算法等(连军艳, 2006)。本研究将采用MML-EM算法进行陕北中鸡勘查区煤厚数据混合分布特征研究。

2 研究区地质概况

中鸡勘查区位于陕北侏罗纪煤田的北部，与神府矿区相邻，是鄂尔多斯盆地中生代中侏罗世含煤沉积——陕北侏罗纪煤田的一部分。其行政区划隶属于榆林市神木县中鸡镇所管辖，北部靠近内蒙古自治区。该地区煤质优良，煤层多且厚，煤炭资源储量丰富，开采地质条件简单，有广阔的发展前景和巨大的开发潜力，是陕北能源化工基地的重要组成部分(陕西省煤田地质局一八五队,2012)。

中鸡勘查区所处的鄂尔多斯盆地是以中生代陆相沉积为主体的大型内陆沉积盆地，构造单元处于鄂尔多斯宽缓的东翼——陕北斜坡上。盆地基底是坚固的前震旦系结晶岩系，故成煤前后的整个地质发展过程继承了深部基底的稳定性。中生代以来，地质史上历次构造运动对本区影响甚微，以垂向运动为主，形成了一系列假整合面，没有发现火成岩，发现少量断层。

中鸡勘查区内地表大部分被现代风积沙、第四系萨拉乌苏组所覆盖，基岩中北部出露。地层总体为走向北东、倾向北西、倾角<1°的单斜构造，未发现明显的褶皱构造，未发现落差>50 m的断层,也无岩浆活动。地层由老到新依次有：三叠系上统永坪组(T3y)，侏罗系中统延安组(J2y)、直罗组(J2z)、安定组(J2a)，白垩系下统洛河组(K1l)，新近系上新统保德组(N2b)，第四系中更新统离石组(Qpl)、第四系上更新统萨拉乌苏组(Qps)、第四系全新统风积层(Qheol)和冲积层(Qhal)。其中含煤地层延安组(J2y)岩性以灰白色-浅灰白色粗、中、细粒长石石英砂岩、岩屑长石砂岩及钙质砂岩为主，次为灰-灰黑色粉砂岩、砂质泥岩、泥岩及煤层，少量炭质泥岩，局部地段夹有透镜状泥灰岩及黄铁矿结核。与下伏永坪组为假整合接触，与上覆直罗组呈假整合接触，厚度147.02～235.89 m，平均厚度201.20 m，总体变化趋势由中部向四周逐渐增厚。

延安组可划分为5个煤组，煤层编号见表1，其中2-2上及2-2下是2-2煤层分岔后上下分层的编号。本区可采煤层有9层，主要可采煤层为1-2下、2-2(2-2上)、3-1、4-3、5-2上，次要可采煤层为1-2下、2-2下、4-2、5-2下。以勘查区内83个钻孔的2-2煤(2-2上)、3-1煤、4-3煤的煤厚数据为例，运用MML-EM算法，对煤厚的混合分布特征进行研究，其中2-2煤分岔后煤厚数据取自2-2上煤，为方便叙述，代号统一简记为2-2煤。

表1 中鸡勘查区延安组分段及煤层编号

3 煤厚数据探索性数据分析及混合分布筛分

3.1 煤厚数据探索性数据分析

传统统计分析方法是以数据总体满足正态假设为依据，并在此基础上建立模型和统计推断。为“让数据说话”，采用探索性数据分析(EDA)方法来展示煤厚数据的统计特征及空间分布特点，在试探出数据的统计特点后再对数据进行进一步分析。注意到本区83个钻孔中有若干钻孔煤层不出现，2-2煤、3-1煤、4-3煤不出现煤层的钻孔数分别为：2，3，9个，于是,首先剔除2-2煤、3-1煤、4-3煤的煤厚为0的数据。图1是该3层煤的煤厚数据的矩阵散点图-直方图-箱线图的叠加综合统计图。由3个煤厚变量的直方图可见：2-2煤、3-1煤、4-3煤均呈现多峰型混合分布特征，从箱线图可见3个煤厚变量的箱线图均反映出煤厚分布是非正态的，并且中位数偏向高值端；3-1煤的煤厚具有若干异常值，特别是特低值成分更为明显。图1中的散点图反映了任意2个煤厚变量之间的相关关系，从中可见，2-2煤与4-3煤之间存在一定的相关性，并且按高值和低值可以分成2组点群；另外2组变量之间的相关性则不明显。

图1 2-2煤、3-1煤、4-3煤煤厚数据的探索性数据分析

将探索性数据分析技术数据用于空间统计中，产生了探索性空间数据分析(ESDA)技术。将2-2煤、3-1煤、4-3煤煤厚数据所在的钻孔空间位置以及3个变量之间的煤厚柱状图绘制投影到勘查区地形图上。柱状图中煤厚为一水平线者表示对应煤层未出现，在图中对应的钻孔符号颜色设置为红色(图2)。由西北向东南，2-2下煤的出现意味着2-2煤开始出现分岔，该分岔界线呈近北东向延伸(见图2中黄绿色虚线AB)。由钻孔资料分析可知，分岔煤层间距约 0.93～32.75 m，平均16.57 m，总的趋势是由北向南间距逐渐增大，到本区东南角又开始有复合趋势。由图2还可见：在该分岔界线AB两侧，2-2煤、3-1煤、4-3煤煤厚具有良好的空间变化规律。2-2煤在本区西北部与中部(AB线左上侧)煤厚普遍较大，且明显厚于3-1煤和4-3煤；而在东南部(AB线右下侧)，2-2煤厚度明显降低，该区以3-1煤煤厚相对占优。4-3煤主要出现在本区西北部和中部；东南部则厚度较薄，甚至未见，未见4-3煤的9个钻孔均出现在该区。在西北部与中部，4-3煤厚与3-1煤厚的比值以大于1为主，而在东南部则小于1；2-2煤厚与3-1煤厚的比值也有类似的结果。

3.2 煤厚数据正态概率投图

由探索性数据分析结果可知，中鸡勘查区2-2煤、3-1煤、4-3煤煤厚数据具有混合总体性，其空间分布特征比较复杂但又有一定规律可循。应用混合分布理论来开展煤厚控制因素研究，为对混合分布形态及分支数有个经验性的认识，绘制了正态概率图来展示2-2煤、3-1煤、4-3煤煤厚数据的混合总体累积概率特征(图3)。按煤矿生产对煤厚进行分类结果表明：2-2煤以厚煤层为主，薄煤层为次，中厚煤层相对较少；3-1煤与4-3煤以中厚煤层为主，其次为薄煤层，部分位置还出现极薄煤层；4-3煤的中厚煤层的层厚以2 m以内占主导，而3-1煤的中厚煤层的层厚在2～3 m区间上有个较明显的集中区。由图3展示的正态概率图可见，2-2煤、3-1煤、4-3煤煤厚数据具有混合分布特征，不能以单一分布如正态分布来描述，混合分支数量可能为2～3个，总体而言分支数量不会太多，各分支的概率密度函数可以用正态分布概率密度函数来刻画，采用高斯有限混合模型来开展混合分布筛分。

3.3 基于MML-EM算法的混合分布筛分

MML-EM算法是EM算法的改良版，采用它来估计子总体的最优个数及正态概率密度函数参数。设迭代收敛时的精度为10-8,分支数的搜索范围为[1,3]，经过迭代计算得到最终参数估值。2-2煤、3-1煤厚数据均筛分出2个分支分布，4-3煤筛分出3个分支分布(表2、图4)。为便于讨论，对2个分支分布情形，按其子总体均值大小分别称为高值子总体和低值子总体，对3个分支情形，则均值位于中间者所对应的第2个分支分布称为中值子总体。

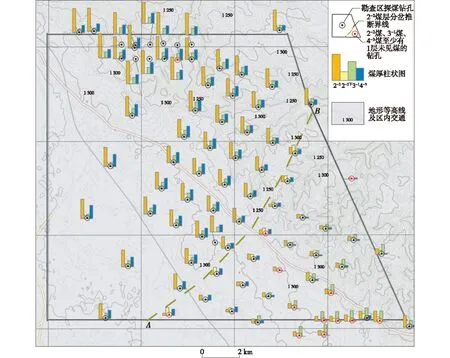
图2 中鸡勘查区探煤钻孔位置及煤厚柱状图

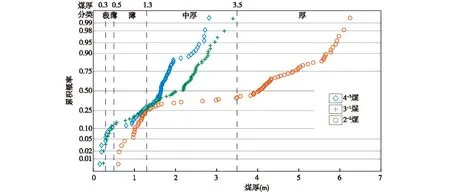
图3 2-2煤、3-1煤、4-3煤的煤厚数据正态概率图

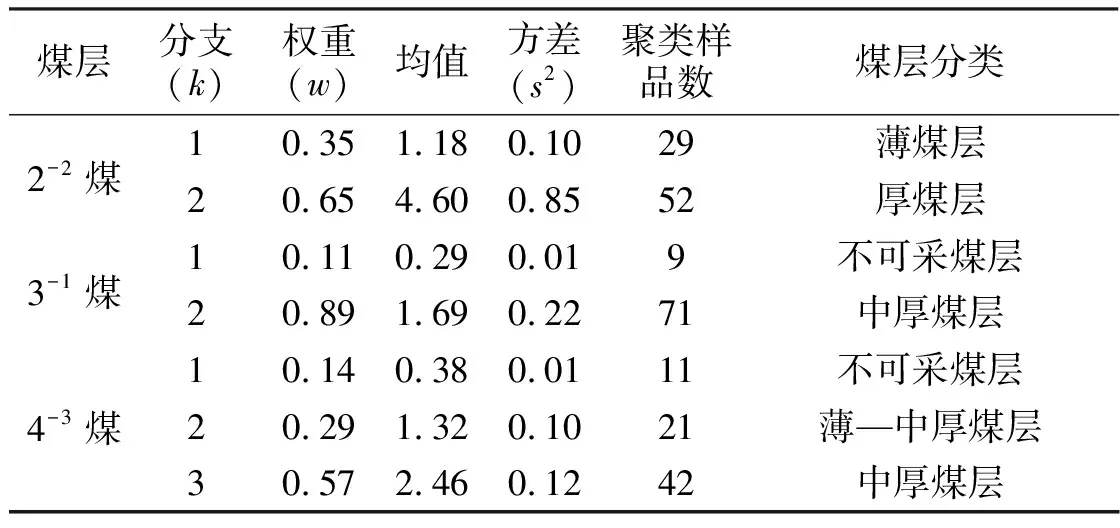
表2 层厚数据高斯混合总体筛分结果

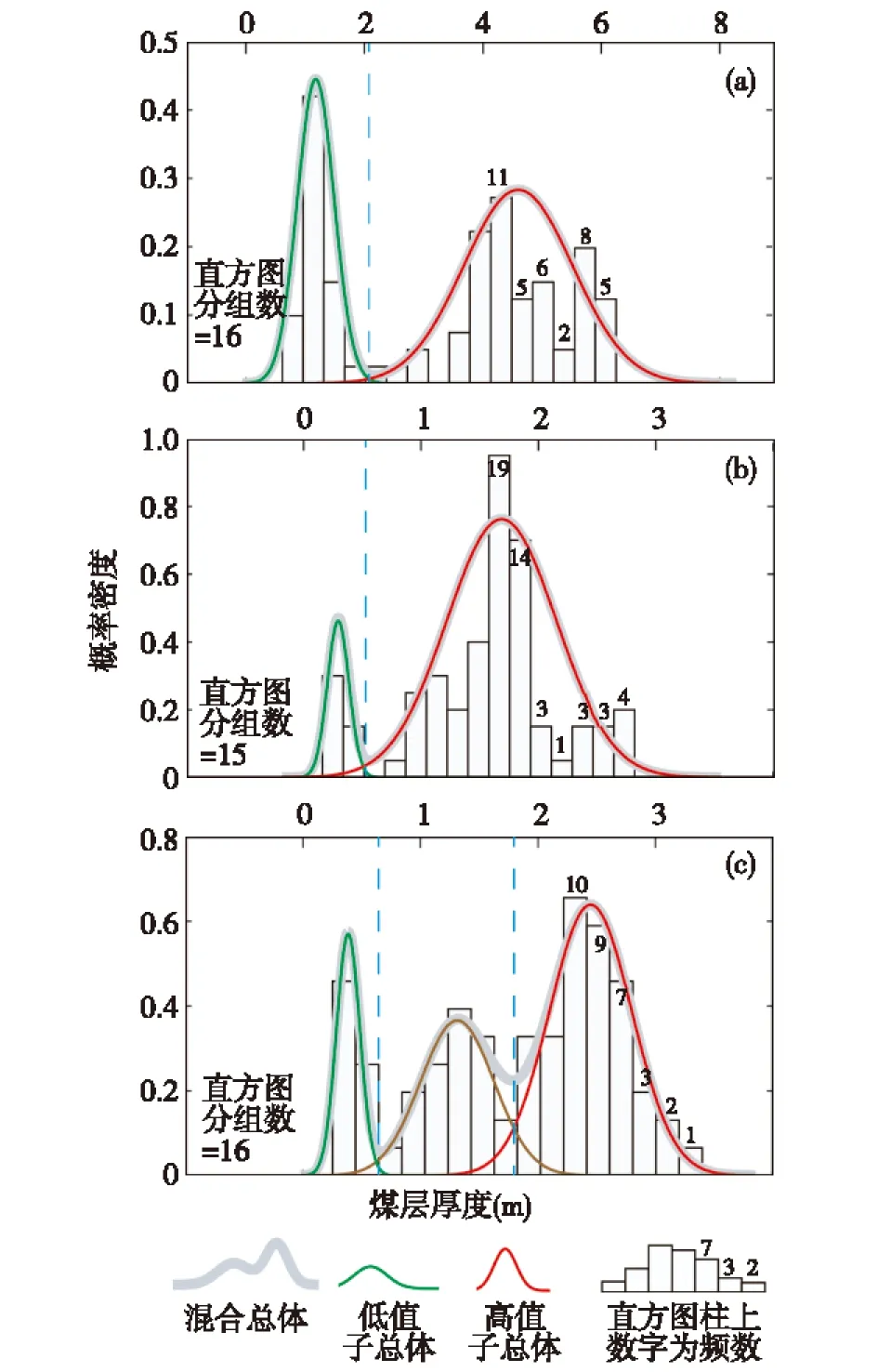
图4 层厚数据高斯混合总体筛分结果

4 讨 论

4.1 煤层厚度与其底板高程的相关关系

应用GeoDA软件(Anselin,2005)对煤层厚度与其底板高程进行了探索性空间数据分析，以期发现煤厚混合分布子总体样本与底板高程之间的统计关系及空间展布特点。图5展示了由GeoDA软件绘制的粒状示意地图及两者的散点图，

图5a示意地图上，各点符号位置近似于钻孔空间位置，点符号大小表示煤厚大小，填充颜色表示煤层底板高程，通过点符号轮廓的差异区分不同的子分布样品。对比2-2煤、3-1煤、4-3煤3层煤底板高程的变化趋势，可见它们有相同的变化趋势，即底板高程由北西向东南总体上逐渐增高，这与“陕北斜坡”的构造形态基本吻合，值得注意的是，3层煤底板高程在不同位置有不同程度的凹陷。2-2煤以分岔界线AB(图5a中的AB线，与图2中的AB线相同)为界正好对应筛分出的2个子总体，西北及中部钻孔所见2-2煤厚属于高值正态总体，分岔后在东南部的钻孔所见2-2煤厚属于低值正态总体，这些低值总体样品总体上分布于勘查区东南部的凹陷区，呈条带状、近北东向展布；在AB线附近钻孔所见的3-1煤厚明显偏低，对应该煤厚混合分布中的低值正态总体，这些低值总体样品分布于勘查区中部3-1煤的凹陷区，呈串珠状、近北东向展布；4-3煤的凹陷区分布在东南角上，呈条带状、近东西向展布，这些位置的煤厚数据服从低值正态总体分布，AB线穿越的区域对应筛分所得子总体为中值子总体。

图5b散点图所展示的煤厚与底板高程显示出一定的规律性。在PQ线左上侧范围内，2-2煤、4-3煤的煤厚与底板高程呈负相关关系，即底板高程越高的地方，煤层越薄；3-1煤煤厚则受底板高程影响较小。在PQ线右下范围内，3-1煤煤厚与底板高程呈正相关关系，2-2煤煤厚也具有类似关系，2-2煤在该区域由于样品数较少，与底板高程的关系不易识别。总体而言，这3个煤层的煤厚混合数据在PQ线右侧与高程的正相关关系还是相对较清晰的，2-2煤以极薄煤层形式出现。

综上所述，底板高程与煤厚有密切关系，高程的变化可能是影响煤厚变化的主要因素。值得指出的是，图5b所示PQ线对于划分2-2煤、4-3煤煤厚样品是有效的，而3-1煤煤厚与其底板高程的关系相对其他2层煤而言表现形式要复杂一些，PQ线所划分的样品与本次研究筛分所得的3个子总体并不对应。若按PQ线将3-1煤样品划分成2个子总体，则煤厚数据近似服从“相交双峰型”混合分布，即其中一个子总体完全重叠在变化范围更宽的另一个子总体之上，所采用的一维EM算法会失效。采用煤厚单变量来研究混合分布，根据图4b中3-1煤煤厚直方图特征，对该煤厚数据理解为近似服从“非相交双峰型”混合分布。在进一步研究中可应用二维EM算法对煤厚及其底板高程2个变量开展混合总体筛法，并探讨其地质意义。

图5 煤层底板高程与煤层厚度变化

4.2 煤层沉积环境推断

根据以往资料，整个陕北侏罗纪煤田构造简单、稳定，没有大的褶皱和断裂，在此大背景下，可从沉积与剥蚀的角度来分析煤层厚度与其底板高程间关系的形成原因。由上述分析可知，在凹陷区及附近煤厚突然变薄是2-2煤、3-1煤、4-3煤共同的变化趋势特点之一。不同的煤层，凹陷区分布位置有所不同。3-1煤凹陷区靠近勘查区中部AB线附近，2-2煤为东南部，4-3煤在东南角上，因此导致煤厚趋势变化随空间位置而不同,煤厚与煤层底板总体上表现为正相关关系。在沉积基底低凹的地区，由于地势突然降低，沉积物的补给量和沉积速度很快(黄克兴等，1991)，因此在沉积过程中，泥沙及砾石等沉积物的沉积速度和补给量总体上大于植物遗体，抢占了植物遗体的补给空间，于是出现现存煤层底板低的区域煤层反而薄的情形，2-2煤的凹陷区出现2-2下煤可能就是这种原因造成的。随着底板地势的逐渐增高且沉积物的补给量和速度有所减缓，植物遗体获得了最佳的沉积机会，于是煤层随着其底板的增高不断变厚，因此可形成本区中的中厚煤层。

在本区更广泛出现的是煤厚与煤层底板呈负相关关系的情形，所涉及煤层含煤性更好。负相关关系的原因可能是由于在区域上，随着底板高程的持续增高，植物遗体来源不断减少而沉积速率逐渐降低，于是导致随着煤层底板增高煤层逐渐减薄的状况。图5b中PQ线左侧，2-2煤、4-3煤底板高程变化幅度可达150 m，煤厚变化幅度也可达3 m左右。在植物遗体来源充足的情况下，结合本区良好的沉积-构造条件，易于形成中厚煤层和厚煤层。

通过图5a所展示的混合分布正态子总体所属样品的空间位置，发现每个子总体在空间上都具有良好的聚集性。2-2煤厚以AB线为界(左上侧为高值子总体样品，右下侧为低值子总体样品)；4-3煤厚以AB线附近(低值子总体样品)与远处(高值子总体样品)来划分，4-3煤在本研究中筛分出3个子总体，在空间上由北西向东南依次为高值子总体—中值子总体—低值子总体，其中中值子总体在空间上处于中间过渡部位，AB线出现在区域内部。总体而言，2-2煤、3-1煤、4-3煤煤厚数据经混合分布筛分都获得了一个极薄—薄层煤厚的低值子总体以及中厚—厚层煤厚的高值子总体，两者可能代表了2种不同的沉积环境，即低值总体指示了沉积物的沉积速度和补给量大于植物遗体的沉积速度和补给量；高值总体正好相反，代表着低值总体代表沉积物的沉积速度和补给量小于植物遗体的沉积速度和补给量。

5 结 论

中鸡勘查区2-2煤以厚煤层为主；3-1煤以中厚煤层为主，局部不可采；4-3煤以中厚煤层为主，局部不可采。2-2煤、3-1煤、4-3煤的煤厚数据具有混合分布特征，采用一维MML-EM算法获得了该3个煤层的煤厚数据的子总体个数及其参数，其中，2-2煤、3-1煤的煤厚数据近似服从由2个子分布组成的混合正态分布，4-3煤厚数据近似服从由3个子分布组成的混合正态分布。

EDA/ESDA技术为发现与理解煤厚数据统计特征、空间分布特征提供了有效的分析手段，特别是良好的可视化手段。初步认为煤厚变化的主要控制因素是底板高程的变化，其中既有正相关关系，也有负相关关系，以前者在本区占主导。正相关关系所指示的煤层厚度达到中厚—厚层级别，煤层主要分布在本区的西北和中部区域；负相关关系所指示的煤层厚度通常较薄，在地理位置上受控于局部凹陷。煤厚数据混合总体筛分获得了低值与高值2个子正态子总体，它们可能分别对应于2种不同的沉积环境，即低值总体指示泥沙及砾石等沉积物的沉积速度大于植物遗体的沉积环境，高值总体则反之，植物遗体的沉积速度和补给量占主导。

中鸡勘查区煤厚数据具有多峰型混合总体分布特征，2-2煤、4-3煤表现为典型的非相交双峰型混合分布；3-1煤可能为非相交双峰型混合分布，也可能为相交双峰型混合分布。可考虑煤厚及其底板高程的二维混合总体分布的筛分，进一步开展关于混合总体分布的研究。

杜文凤,彭苏萍.2010.利用地质统计学预测煤层厚度[J].岩石力学与工程学报,29(增刊1):2762-2767.

高荣斌,贺志强,来争武,等.2011.豫西新安煤田煤层厚度变化规律及其控制因素[J].煤田地质与勘探,39(4):13-15,19.

黄克兴,夏玉成.1991.构造控煤概论[M].北京:煤炭工业出版社.

琚宜文,王桂梁,胡超.2002.海孜煤矿构造变形及其对煤厚变化的控制作用[J].中国矿业大学学报,31(4):374-379.

李恒堂,吕志发.1995.鄂尔多斯盆地延安组控煤古构造趋势分析[J].煤田地质与勘探,24(5):5-8.

连军艳.2006.EM算法及其改进在混合模型参数估计中的应用研究[D].西安:长安大学.

刘向冲,侯翠霞,申维,等.2011.MML-EM方法及其在化探数据混合分布中的应用[J].地球科学：中国地质大学学报, 36(2):355-359.

柳贵东,山拜·达拉拜.2011.基于EM算法的非高斯噪声参数估计[J].通信技术,44(1):151-153.

苗霖田等.2008.神木北部矿区5—2煤层厚度及其底板高程趋势分析[J].煤田地质与勘探,36(3):12-15.

陕西省煤田地质局一八五队.2012.陕西省陕北侏罗纪煤田榆神矿区中鸡勘查区详查报告[R].榆林:陕西省煤田地质局一八五队.

王琳.2005.可视化概率图解法软件的研制与应用[D].北京:中国地质大学(北京).

辛克莱.1976.概率图在矿床勘探中的应用[M].北京:地质出版社.

翟裕生,姚书振,崔彬.1996.成矿系列研究[M].北京:中国地质大学出版社.

张锋.2012.闪锌矿矿石标本便携式XRF测量数据混合总体筛分及其地质意义[D].武汉:中国地质大学(武汉).

张士峰.2004.混合正态分布参数极大似然估计的EM算法[J].飞行器测控学报,23(4):47-52.

张展适,吴信民.1998.概率图法在茅排金矿的应用[J].华东地质学院学报,21(3):254-256.

赵鹏大,胡旺亮,李紫金.1983.矿床统计预测[M].北京:地质出版社.

ANSELIN L.2005-03-06.Exploring Spatial Data with GeoDaTM:A Workbook[M/OL]. http://geodacenter.asu.edu/system/files/geodaworkbook.pdf.

DEMPSTER A P, LAIRD N M, RUBIN D B.1977.Maximum likelihood from imcomplete data via the EM alogorithm[J].Journal of the Royal Statistical Society:Series B,39:1-38.

FIGUEIREDO M A T,JAIN A K.2002.Unsupervised learning of finite mixture models[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,24(3):381-396.

MCLACHLAN G,PEELD.2000.Finite Mixture Models[M].New York,USA:John Wiley & Sons Inc.