COMPASS三频数据线性组合优化选取分析

刘国超， 黄张裕， 徐秀杰，冯剑桥

(河海大学 地球科学与工程学院,江苏 南京 210098)

COMPASS三频数据线性组合优化选取分析

刘国超， 黄张裕， 徐秀杰，冯剑桥

(河海大学 地球科学与工程学院,江苏 南京 210098)

以北斗卫星I支路频点为例，从消除或减弱电离层影响、对流层影响和观测噪声与多路径误差3个方面分析COMPASS三频数据线性组合的优化选取问题，并通过MATLAB模拟，给出一些典型的组合，分析它们可能的应用，为COMPASS三频数据线性组合的优化选取提供一些借鉴。

北斗卫星；三频数据；线性组合；优化选取；电离层延迟；对流层延迟；观测噪声

COMPASS导航定位系统是我国自主研制的新一代卫星导航定位系统，不同于GPS，COMPASS有其自身的时间系统、坐标系统和信号体制。COMPASS系统采用北斗时(BDT)，起算时间为2006年1月1日UTC 0时，采用国际单位制秒为基本单位，连续累计，不闰秒，其与UTC的偏差保持在100 ns以内。坐标系统采用2000中国大地坐标系(CGCS2000)，信号体制不同于GPS的码分多址，COMPASS采用频分多址技术，有3个载波频段，分别是B1，B2，B3[1-3]。可以预见，COMPASS系统在高精度定位和实时导航定位应用中，最需要解决的是上述3种载波相位观测值整周模糊度的确定问题，以及如何消除电离层延迟、对流层延迟和观测噪声的影响。借鉴GPS应用的经验，具有相应特性的组合观测值能有效地解决上述问题。为此，本文以北斗卫星I支路频点为例，从消除或减弱电离层影响、对流层影响和观测噪声与多路径误差3个方面分析了COMPASS三频数据线性组合的优化选取问题，为之后北斗三频数据线性组合的优化选取提供一些借鉴。

1 COMPASS三频数据线性组合

北斗卫星发射3个频率的载波信号，每个频率分为I和Q两个支路，每个支路上调制3种不同类型伪随机码，分别可以得到宽相关(W)、窄相关(N)和抗多径(A)3个类型的伪距观测量[4]。以I支路为例，其各频点的特征如表1所示。

表1 COMPASS频率及调制信息

设北斗卫星载波相位观测方程为

Li[m]=d+λiN-qiΔion.

(1)

其中：载波相位观测量Li以m为单位；d为包含接收机钟差、卫星钟差和大气延迟的伪距观测值；λi为载波波长；N为整周模糊度；Δion是以m为单位的B1载波的电离层延迟；qi为对应的比例因子。根据电离层延迟的色散效应，qi可表示为qi=(fB1/fBi)2，i=1,2,3。代入表1 所示频率，得到q1=1,q2=1.672,q3=1.514。

理论上，任何可以使模糊度参数保持整数特性的整数都可以作为北斗三频数据线性组合系数。设组合系数为a,b,c，则以周为单位的组合相位φB=φ(a,b,c)可表示为

φB[cy]=aφ1[cy]+bφ2[cy]+cφ3[cy].

(2)

通过式Li[m]=λiφi[cy]，可以得到以周为单位的组合载波观测方程为

aN1+bN2+cN3-

(3)

由上式可知，组合后的整周模糊度NB=N(a,b,c)=aN1+bN2+cN3，对应的组合频率为fB=f(a,b,c)=afB1+bfB2+cfB3。设f0为北斗卫星基准频率，则f0=2.046 MHz，由此得到fBi=kif0,(i=1,2,3)，其中：k1=763,k2=590,k3=620，代入组合频率公式可得

fB=afB1+bfB2+cfB3=f0(763a+590b+620c).

(4)

其中,令k=763a+590b+620c，则组合波长λB=c/fB=λ0/k，λ0=c/f0≈146.526 m。 由此可知，k值的选取决定了北斗三频组合观测值的波长和频率。以k为基础，可以定义以下3类不同的线性组合：

1)宽巷组合：1≤k≤590。组合波长大于北斗三频数据最大波长，即λB≥λ2=0.248 m。

2)中间巷组合：590≤k≤763。组合波长介于北斗三频数据最大与最小波长之间，即0.192=λ1≤λB≤λ2。

3)窄巷组合：k≥763。组合波长小于北斗三频数据最小波长，即λB≤λ1。

2 COMPASS三频数据线性组合的优化选取标准

2.1 消除或减弱电离层影响

由式(3)可知，以m为单位的北斗三频数据线性组合电离层延迟放大系数为

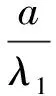
(5)

其中，λB为组合波长，其他参数和前面定义一样。由此可知，如果在B1载波上发生10 cm的电离层延迟误差，那么将导致组合载波上10×IBcm的电离层延迟误差。在公式两边同乘以λ1/λB，则可得到以周为单位的电离层延迟放大系数为

(6)

2.2 消除或减弱对流层影响

对流层延迟不同于电离层延迟，由于不具备色散效应，所以其线性组合放大系数为

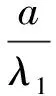
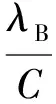
(7)

2.3 减弱观测噪声和多路径影响

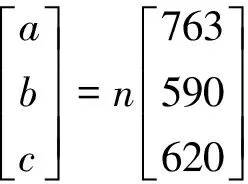
(8)

时可以最大限度地减小观测噪声的影响[6]。式(8)在空间中定义了一条直线，越靠近这条直线的组合其减少观测噪声的效率就越高。但是由于组合系数的整数约束条件，大部分的组合系数并不能落在式(8)定义的直线上。

3 COMPASS三频数据最优线性组合的选取

前面的章节中，分别单独地介绍了北斗三频数据线性组合如何消除或减弱电离层延迟、对流层延迟和观测噪声影响。但是在北斗实际应用过程中，各种观测误差源和噪声总是不同程度地同时出现，因此，寻求一种能同时消除各种误差的最优组合就很重要。要使得总的观测噪声减小，那么电离层延迟误差和对流层延迟误差应该减小，组合系数作为一个空间点应该接近。

3)原点(0,0,0)。

电离层延迟平面与对流层延迟平面之间夹角θ可表示为

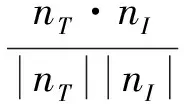
(9)

其中：nT,nI分别表示无电离层延迟平面和无对流层延迟平面的法向量；|nT|,|nI|分别为nT,nI的2范数。同样可以得到GPS的θ角为14.6°，由于北斗的θ角比GPS的更小，夹在两平面锐角之间的组合系数离两平面垂直距离之和比GPS小，所以北斗三频数据组合要比GPS更有优势，具体情况如图1所示。

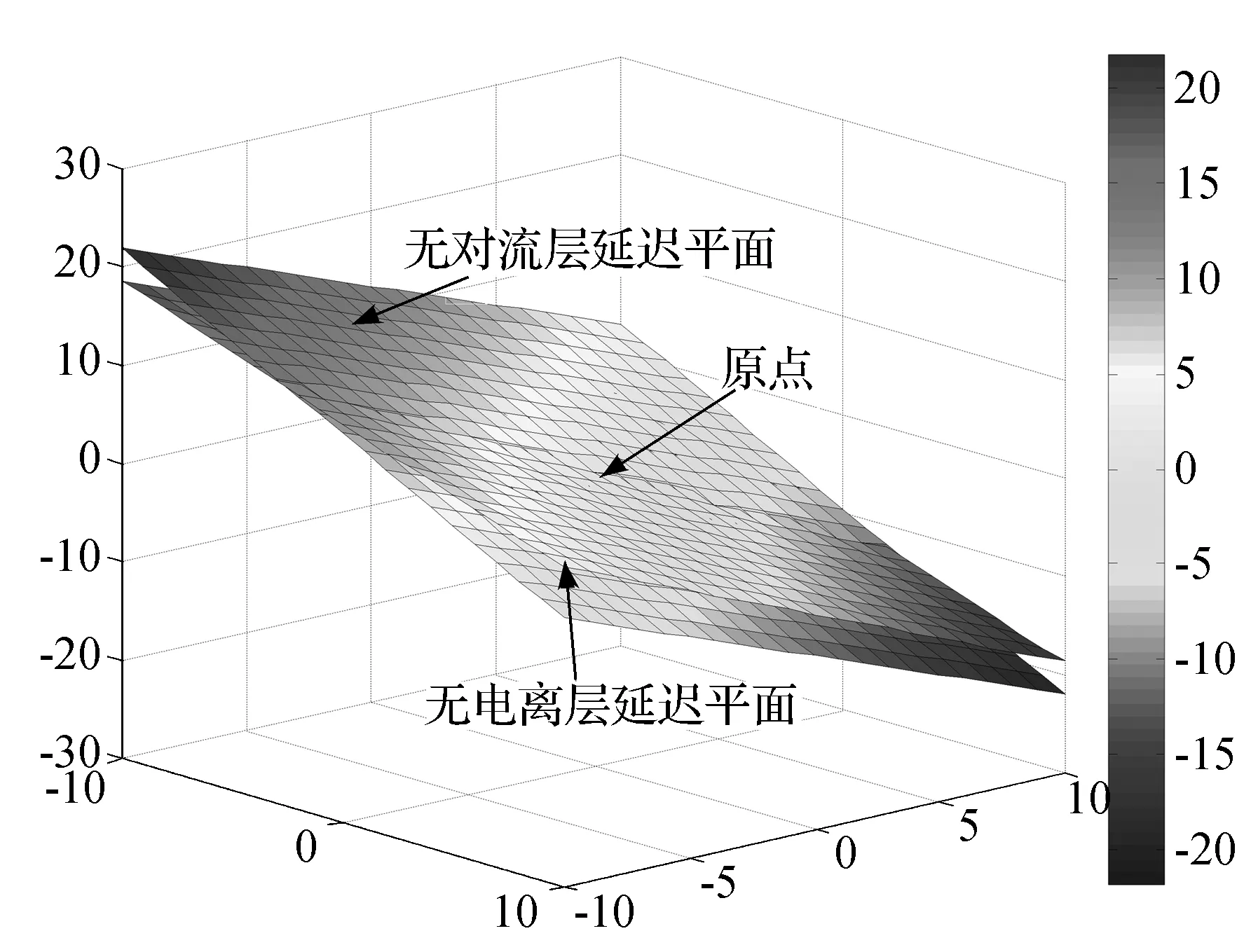
图1 Compass三频无电离层和无对流层延迟组合图

一种好的线性组合要根据各种误差源的大小来确定。比如说，在长基线测量中，电离层延迟误差和对流层延迟误差在各种误差源中占主要地位，这种情况下，应该优先选择靠近无电离层延迟平面和无对流层延迟平面的组合而不是靠近原点的组合；在短基线测量中，电离层延迟误差和对流层延迟误差经过双差后基本消除，主要剩余观测误差，这样情况下，应该优先选择靠近原点的组合。

在北斗三频线性组合中，为了最大限度地减小白噪声和多路径效应的影响，北斗三频数据线性组合系数作为一个空间点应该靠近。

最大限度减小观测噪声影响的空间直线与无电离层延迟平面之间的夹角

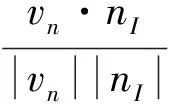
(10)

其中：vn，|vn|为空间直线的方向向量和2范数；nI,|nI|为无电离层延迟平面的法向量和法向量2范数。由于最大限度减小观测噪声影响的空间直线与无电离层延迟平面之间的夹角很大，这就出现一个矛盾，当组合系数空间点靠近无电离层延迟平面时就会远离最大限度减小观测噪声影响的空间直线；当组合系数空间点靠近最大限度减小观测噪声影响的空间直线时就会远离无电离层延迟平面。具体情况如图2所示。

图2 Compass三频线性组合减小噪声图

根据上面的理论，通过MATLAB软件解算，给出了几种典型的北斗三频数据线性组合，如表2所示。

表2中，未加粗的COMPASS三频线性组合为长波长组合，其优势在于整周模糊度相对容易确定，可用于解算基线时快速确定整周模糊度，其中(-1，-5，6)、(1，4，-5)和(0，-1，1)组合的波长较长，同时它们的电离层延迟和观测噪声很小，对于快速确定整周模糊度是很好的选择。加粗的COMPASS三频线性组合为弱电离层延迟组合，在长基线导航定位和实时定位中有重要意义。其中(3，11，-14)组合不仅有较长的波长(1.48 m)，而且电离层延迟很小(放大系数接近于0)，对于长基线模糊度解算和实时导航定位有重要意义。观察加粗的COMPASS三频线性组合，会发现电离层延迟放大系数很小，但其对应的噪声放大系数却很大，这是由于最大限度减小观测噪声影响的空间直线与无电离层延迟平面之间的夹角很大的缘故。

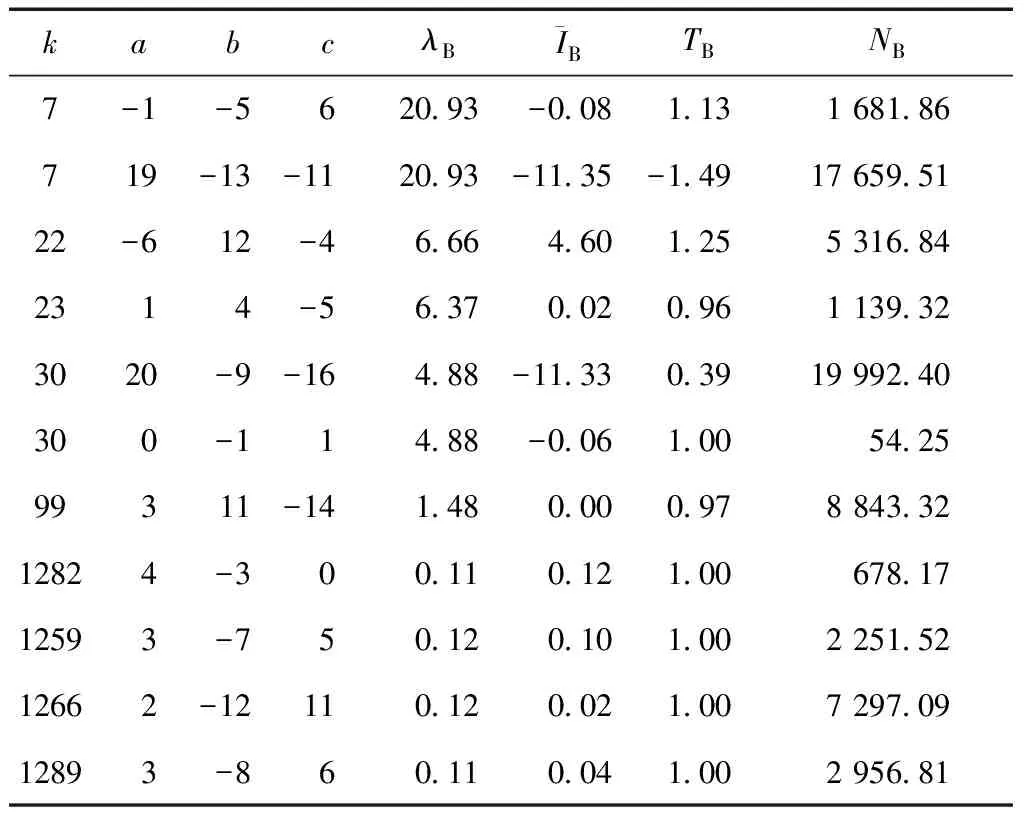
表2 典型的COMPASS三频数据线性组合

4 结束语

本文系统地分析了COMPASS三频数据线性组合的优化选取问题，首先分析了COMPASS三频数据线性组合的数学机理，进而从消除或减弱电离层延迟、对流层延迟影响和观测噪声方面入手，阐述了北斗三频数据线性组合的优化选取标准。根据上述标准，结合实际应用情况，提出了COMPASS三频数据线性组合系数选取的建议如下：

1)由于COMPASS的基准频率(2.046 MHz)是GPS基准频率(10.23 MHz)的1/5，所以相对于GPS，COMPASS系统可以形成更多长波长的优良线性组合。这将极大地减小整周模糊度的搜索空间，提高确定整周模糊度解的效率。

2)用双差法解算短基线时，两站的大气延迟空间相关性强，可通过求差基本消除其影响，此时应该寻求适当的组合观测值能快速准确地确定整周模糊度和提高观测精度，这样的组合应该有较高的观测精度和较长的观测波长，如(-1，-5，6)、(1，4，-5)和(0，-1，1)组合。而在长基线相对定位中，电离层延迟和对流层延迟对定位结果影响很大，此时应该选取弱电离层延迟和弱对流层延迟组合，如(1，4，-5)和(3，11，-14)组合。

3)周跳的探测与修复和整周模糊度确定问题是载波相位测量的关键问题。北斗三频数据线性组合可以形成更多长波长、弱电离层、低噪声的优良组合。可以联合利用这些优良组合组成探测矩阵探测周跳和确定整周模糊度[7-8]。比如整周模糊度确定中，CIR方法就是利用不同伪距和组合其波长不同的特点，先解算出波长最长的模糊度，然后作为已知值求解波长次长的模糊度，“逐级”确定模糊度。

[1]唐祖平，周鸿伟，胡修林，等.Compass导航信号性能评估研究[J].中国科学，2010,40(5)：592-602.

[2]杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报，2010,39(1)：1-6.

[3]刘根友，郝晓光，陈晓峰，等.对我国二代卫星导航系统覆盖范围向北扩展星座方案的探讨[J].大地测量与地球动力学，2007，27(5)：115-118.

[4]周巍，郝金明，冯淑萍.北斗三频数据周跳的探测方法[J].测绘科学技术学报，2012，29(2)：87-90.

[5]TODD RICHERT.The Impact of Future Global Navigation Satellite Systems on Precise Carrier Phase Positioning[D].Geomatics Engineering Department, University of Calgary, UCGE Report No.20218.

[6]TODD RICHERT ,Naser EI-Sheimy.Optimal linear combinations of triple frequency carrier phase data from future global navigation satellite systems[J].GPS Solut(2007)11:11-19.

[7]黄令勇，宋力杰，王琰，等.北斗三频无几何相位组合周跳探测与修复[J].测绘学报，2012,41(5)：763-768.

[8]ZEMIN WANG,YUE WU.Triple-Frequency Method for High-Order Ionospheric Refrative Error Modelling in GPS Modernization[J].Journal of Global Positioning Systems,2005,4(1-2):291-295.

[责任编辑：刘文霞]

A systematic investigation of optimal carrier-phase combinations for triple-frequency COMPASS

LIU Guo-chao，HUANG Zhang-yu，XU Xiu-jie，FENG Jian-qiao

(School of Earth Sciences and Engineering, Hohai University, Nanjing 210098, China)

Taking the COMPASS system I frequency as the example, from three aspeets of eliminating or mitigating the ionospheric delay, tropospheric delay and observation noise, it analyzes systematically the optimal selection of COMPASS triple-frequency coefficient of linear combination.At last, by MATLAB simulation, some typical combinations are given and analyzed on the possible applications, which can provide some reference to the optimal selection of COMPASS triple-frequency linear combination.

triple-frequency data; linear combination; ionospheric delay; tropospheric delay;observation noise

2013-08-22

刘国超(1989- )，男，硕士研究生.

P228；V249.3

：A

：1006-7949(2014)09-0032-04