基于EIV模型的稳健估计

楚 彬，范东明，刘 波，秦 宁

(西南交通大学 地球科学与环境工程学院，四川 成都 610031)

基于EIV模型的稳健估计

楚 彬，范东明，刘 波，秦 宁

(西南交通大学 地球科学与环境工程学院，四川 成都 610031)

EIV(error-in-variables)模型同时考虑观测向量和系数矩阵的误差，自提出以来便得到广泛应用。目前针对EIV模型的整体最小二乘解法(TLS)假设观测值仅含有偶然误差，当观测值存在粗差时其解并不是最优的。文中通过选定合适的权函数，结合加权整体最小二乘迭代算法，导出基于EIV模型的稳健整体最小二乘迭代解法(RTLS)。线性拟合实验表明，文中方法能对粗差进行定位，且估计量受粗差影响较小，具有稳健性。

EIV模型；整体最小二乘估计(TLS)；稳健估计；稳健整体最小二乘(RTLS)；线性拟合

经典的Gauss-Markov模型假定函数模型已知、非随机，并且认为系数矩阵是可以精确求定的，仅假定观测值向量包含随机误差[1]。在许多实际问题中如数字地面模型拟合、大地测量反演、GIS空间数据分析、滑坡监测和坐标变换等数学模型中，观测向量和描述函数模型的系数矩阵均由观测数据组成，两者都包含随机误差[2]。这类平差模型称为EIV(error-in-variables)模型。由于EIV模型同时考虑观测向量和系数矩阵的误差，因此采用经典最小二乘估计方法(LS)对其进行估计则是有偏的[3]。针对此模型，Golub等人于1980年提出了著名的奇异值分解算法(SVD)，并将其命名为整体最小二乘法(TLS)[4]，自此，整体最小二乘估计引起了各领域的广泛关注。除奇异值分解算法外，还有经典的拉格朗日方法[5]，也可作为非线性Gauss-Helmert模型处理[6]。以上的解法都是在观测向量和系数矩阵仅存在随机误差的前提下进行的，当观测向量和系数矩阵还存在粗差时，则模型歪曲，造成参数估计严重失实。

稳健估计法能够保证所估的参数不受或少受模型误差(首先指的是粗差)的影响，主要用来发现粗差和对粗差进行定位[7]。Choi等最早对EIV模型进行稳健整体最小二乘估计[8]，但是其方法基于传统的假设检验，仅适用于观测向量或系数矩阵只含有一个粗差的情况。陈义等提出基于非线性Gauss-Helmert模型的选权迭代总体最小二乘解法[9]，虽能获得稳健的参数估计，但是其模型协方差阵结构特殊，未考虑观测量之间的相关性，在某些案例中不适用，而且不能解决重复元素的问题。本文通过选择合适的权函数，结合Mahboub提出的改进的加权整体最小二乘迭代解法(WTLS)[10]，导出稳健整体最小二乘迭代解法(RTLS)。通过迭代，含粗差观测值的权函数元素的值会逐步趋近于0，不含粗差观测值的权函数元素变化不大，函数模型具有抗拒粗差的本领，待估参数受粗差的影响较小。

1 EIV模型和加权整体最小二乘解(WTLS)

1.1 EIV模型

观测变量含有误差的EIV模型的线性函数关系式为[11]

y-ey=(A-EA)x.

(1)

式中：y为含有随机误差ey的m维效应量观测向量，A为含有随机误差EA的m×n维自变量观测值或其函数，x为n维待估参数向量。

随机误差具有如下统计性质：

(2)

实际应用发现，很多情况下系数矩阵中各元素间并不是完全相互独立的，系数矩阵中的元素可能重复出现，或某个元素是以某些元素为自变量的函数。因此，本文采用Mahboub提出利用一定原则构造系数矩阵的协方差矩阵[11]。

1) 如果系数阵的某个元素重复出现，认为这两个元素100%相关，因此，这两个元素之间的协方差等于重复元素的自方差。

2) 假如系数阵的某个元素以其相反数的形式重复，认定这两个元素100%负相关，因此，这两个元素之间的协方差等于重复元素的自方差的相反数。

3) 如果系数阵的某个元素是常数，认为其方差为0。

4) 系数阵中两个不同元素，若两者明显相关，他们的协方差即为其实际值，否则为0。

5) 上述规则在同方差情况中同样适用，若元素是随机数只需用数字1作为其方差，若是常数其自方差为0。

1.2 加权整体最小二乘解(WTLS)

WTLS估计准则为

(3)

加权整体最小二乘实质就是在极值条件式(3)和误差方程式(1)的约束条件下求得X的最佳估值。按Lagrange乘数法求解，构成目标函数为[5]

2λ[y-Ax-ey+(xT⊗Im)eA].

(4)

式中：λ为n×1维拉格朗日乘数向量，Im为m×m维单位矩阵。

为求得Φ的极小值，将上式对ey，eA，λ和x求偏导，并令其为0。

(5)

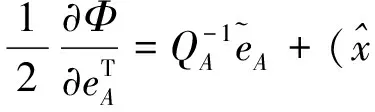
(6)

(7)

(8)

由式(5)和式(6)可求得残差预测值为

(9)

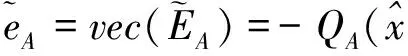
(10)

在导出残差预测公式后，采用Mahboub提出的改进的加权整体最小二乘解法求得待估参数x，其迭代过程如下：

1) 根据上文提到的五原则构造系数矩阵的协方差矩阵QA。

2 稳健整体最小二乘解(RTLS)

2.1 权函数的选取

1）实验的进行不能顾此失彼，对于单桩竖向抗压承载力实验来说，为了避免荷载过重造成仪器损坏，影响实验数据的准确，必须进行必要的操作过程设计规范和细节控制说明，比如：当地基周围土壤隆起时，其观测点的荷载-沉降曲线必然出现陡降，实验中要注意记录陡降前后的荷载数值。此外，当地基基础桩后一次的沉降幅度超过前一次沉降幅度的2倍时，表明沉降过程尚未稳定，因此，要注意记录前一级的荷载数值。最后，在细节把控上，荷载-沉降曲线一定要按照信号传感器反馈的时间曲线进行绘制，必要的情况下，增加辅助曲线，增加检测结果的准确性。

以上的WTLS解仅适用于观测向量和系数矩阵仅含有偶然误差的情况，当其还含有粗差时则会引起模型歪曲，造成参数估计严重失实。为了达到估值稳健的目的，在目标函数式中应加入合适的权函数，使它具有抗拒粗差的本领，而不受粗差的影响。权函数有多种，目前最为著名的有最小范数法、Huber权函数、Hampel权函数和Krarup(丹麦法)权函数等。本文以Huber权函数为例，并根据文献[12]的建议对其稍作改进，所得权函数如下：

(11)

2.2 稳健整体最小二乘解(RTLS)

定理1：假设A为n×n维实对称矩阵，那么则有n×n维正交矩阵S和对角矩阵U(U中对角线上的元素为A的特征值)，使得STAS=U,STS=In。

将QA进行Schur分解可得QA=SUST。结合1.2中加权整体最小二乘解(WTLS)和文献[13]的最小二乘稳健估计方法，可得稳健整体最小二乘解(RTLS)，迭代过程如下：

其中：Wy(i)和WA(i)由式(11)确定，(·)-0.5为矩阵·的算术平方根逆根。在迭代过程中，根据式(9)和式(10)可求得每次迭代的残差预测值，然后将其带入式(11)对权函数进行更正。通过迭代，含粗差观测值的权函数元素的值会逐步趋近于0，不含粗差观测值的权函数元素变化不大。因此，此方法不仅可以对粗差进行定位，而且所估参数受粗差影响较小，具有稳健性。

3 线性拟合实验分析

3.1 观测值仅含有偶然误差

为了考察稳健整体最小二乘方法(RTLS)的效果，通过编写本文所讨论方法的程序，对平面回归算例进行计算并与LS和WTLS方法进行比较。算例如下：设有平面方程z=1.5+1.6x-1.2y，取满足平面方程的8组数值(不含误差)统计于表1，然后对x和y添加ε1∈[-0.3～0.3]的随机误差得到组成系数矩阵的观测值，对z添加ε2∈[-0.2～0.2]的随机误差构成与系数矩阵不同精度的观测向量的值，并将其统计于表2。

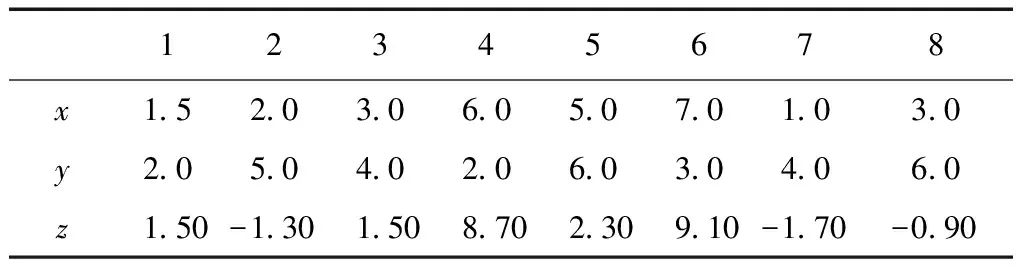
表1 模拟真值统计

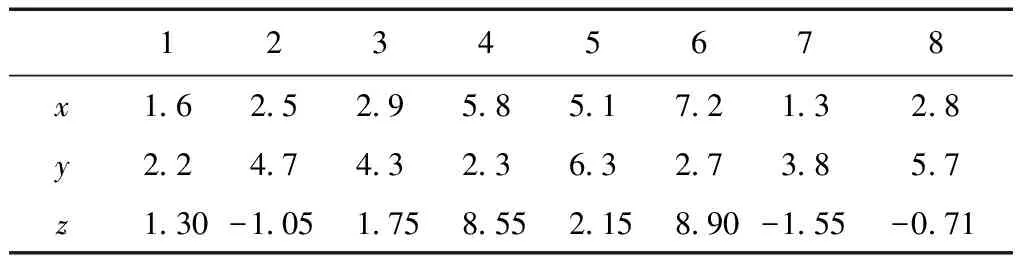
表2 仅含有偶然误差模拟观测值统计

对表2中的模拟观测数据分别采用LS、WTLS、RTLS进行计算，所得待估参数统计见表3。

表3 参数估值统计

由表3可以看出，当系数矩阵含有误差时，采用WTLS和RTLS参数估计精度高于LS。由于观测值仅含有偶然误差，在采用RTLS进行迭代的过程中，权函数保持不变，因此，RTLS和WTLS所得结果相同。

3.2 观测值含有偶然误差和粗差

为了验证RTLS的稳健性，在表2中第6组模拟观测值中x和z分别添加2.0和1.0的粗差，其余组不变，然后采用LS、WTLS和RTLS对平面方程系数进行估计，所得结果统计见表4。

由表4可知，当观测值混入粗差时，RTLS估计效果明显好于LS估计和WTLS估计。这是由于在RTLS迭代过程中，含粗差观测值的权函数元素的值会越来越小，并逐步趋近于0，不含粗差观测值的权函数元素变化不大。因此，可以通过观察迭代过程中权函数元素数值的变化来确定粗差所在位置。在本次试验中，仅x2、x6、y3、y4和z6的权函数值发生变化，图1为迭代过程中权函数值变化曲线图。

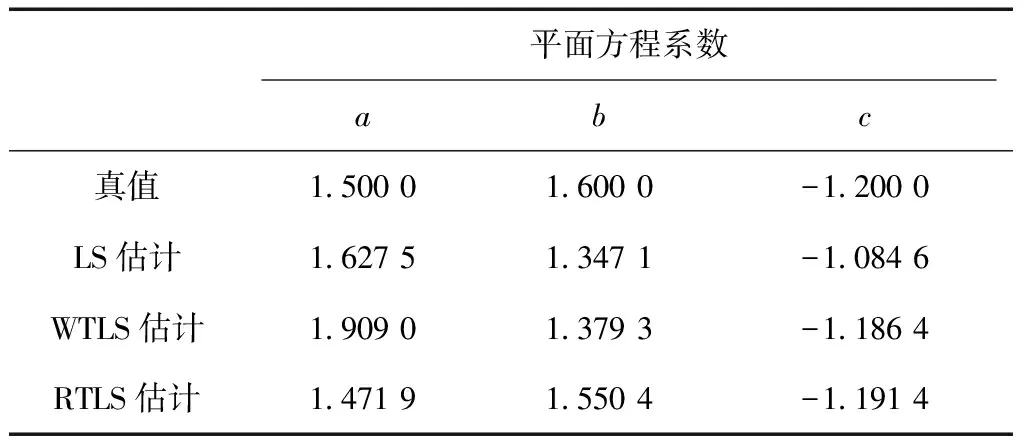
表4 参数估值统计

图1 权函数值变化曲线图

由图1可知，含有粗差的x6和z6观测值权函数数值变化较快，随着迭代过程，其值越来越小。平差过程就是误差分配的过程。本方法采用平差后的残差来确定权函数，当观测值混入粗差时必然会影响到其他不含粗差的观测值，因此，也就解释了为何不含粗差的x2、y3和y4观测的权函数也会随着迭代过程发生变化。

4 结论与不足

EIV模型同时考虑观测向量和系数矩阵的误差，因此自提出以来便得到各个领域广泛的研究。针对EIV模型的估计方法统称为整体最小二乘解。整体最小二乘经过几十年的发展，研究者们已经提出了各种各样的解法。然而这些解法主要都是考虑EIV模型中的偶然误差，关于EIV模型的可靠性理论研究相对薄弱。本文针对EIV模型混入粗差的情况，导出稳健整体最小二乘迭代解法(RTLS)。实验表明，RTLS通过观察迭代过程中权函数元素数值的变化来确定粗差所在位置，且其参数估值受粗差影响较小，具有稳健性。然而，本文导出的RTLS解法是一种验后方法，其中权函数是根据每次迭代平差后的残差来确定的，那些不含粗差的观测值在平差过程中必然会受到含粗差的观测值的影响。因此，如何在验前对平差模型进行可靠性检验还有待进一步的研究与探索。

[1]陶本藻，邱卫宁.误差理论与测量平差[M].武汉：武汉大学出版社，2012.

[2]刘经南，曾文宪，徐培亮.整体最小二乘估计的研究进展[J].武汉大学学报：信息科技版，2013,38(5)：505-512.

[3]邱卫宁，陶本藻，姚宜斌，等.测量数据处理理论与方法[M].武汉: 武汉大学出版社，2008.

[4]GOLUB G H, VAN LOAN CH.An Analysis of the Total Least Squares Problem[J].SIAM Journal on Numerical Analysis, 1980,17(6):883-893.

[5]SCHAFFRIN B, ANDREAS W.On Weighted Total Least squares Adjustment for Linear Regression [ J].Journal of Geodesy, 2008, 82(7):415-421.

[6]NEITZEL F.Generalization of Total Least-Squares on Example of Unweighted and Weighted 2D Similarity Transformation [J].Journal of Geodesy, 2010, 84(12):751-762.

[7]李德仁，袁修孝.误差处理与可靠性理论[M].武汉：武汉大学出版社，2002:243-255.

[8]CHOI Y J, KIM J Y, SUMG K M.A Robust Algorithm of Total Least Squares Method[J].IEICETRANS,Fundamentals,1997,7(E80-A):1336-1339.

[9]陈义，陆珏.以三维坐标转换为例解算稳健总体最小二乘方法[J].测绘学报，2012,41(5):715-722.

[10]VAHID MAHBOUB.On weighted total least-squares for geodetic transformations[J].Journal of Geodesy, 2012,86(5): 359-367.

[11]CHI LUN CHENG, MASTRONDRDL N, PALGE C.Total least squares and errors-in-variables moseling [J].Computational Statistics and Data Analysis,2007,52:1076-1079.

[12]V MAHBOUB, A R AMIRI-SIMKOOEI, M A SHARIFI.Iteratively reweighted total least squares: a robust estimation in errors-in-variables models[J].Survey Review,2013,45(329):92-99.

[13]KRARUP T, JUHL J, KUBIK K.Gotterdammerung over least squares adjustment[J].Proceedings of 14th Congress of the International Society of Photogrammetry,1980,B3: 369-378.

[14]卜长江，罗跃生.矩阵论[M].哈尔滨：哈尔滨工程大学出版社，2007.

[责任编辑：刘文霞]

Robust estimation based on EIV model

CHU Bin, FAN Dong-ming, LIU Bo ,QIN Ning

(School of Earth Sciences and Environmental Engineering,Southwest Jiaotong University, Chengdu 610031，China)

EIV (error-in-variables) model has been widely used sin ce it is proposed as taking both the error of the observation vector and the coefficient matrix into account.However, the least squares solution for the EIV model which is called total least squares(TLS) assuming observations only contain accidental error, when there is a gross error in the observations,the solution is not optimal.By selecting an appropriate weight function, combined with the weighted total least squares (WTLS), a robust estimate called robust total least squares (RTLS) is proposed based on the EIV model.The linear fitting experiments show that the proposed method can locate gross errors, and the estimated amount is less affected by gross error, with robustness.

EIV model; total least squares(TLS); robust estimate; robust total least squares(RTLS); liner fitting

2013-08-11

楚 彬(1990-)，男，硕士研究生.

P207

：A

：1006-7949(2014)09-0017-04