模糊聚类分析方法在土地整治分区中的应用

鲁红英, 肖思和, 杨 尽

(成都理工大学 信息科学与技术学院,成都 610059)

土地整治是对不合理利用、低效利用和未利用的土地进行深度治理，对自然灾害损毁和生产建设破坏的土地进行修复利用，以提高土地利用效率的活动[1]。如何编制科学合理的土地整治规划，其中土地整治分区是一个非常重要的内容。国内许多学者对土地综合整治分区和土地利用分区提出了一些方法并取得一定的成效。比如，毛美桥等人提出了土地综合整治分区和土地整治功能分区的原则和确定方法[2]，巫晓东总结了土地利用分区研究进展并开展了方法研究[3]，王虚提出了聚类分析在土地利用分区中的应用[4]。随着《全国土地总体规划纲要(2006—2020)》和《全国土地整治规划(2011—2015)》文件的颁布，新一轮的土地整治规划编制工作已在全国各地相继开展，而本轮土地整治规划编制和以往规划编制在范围、内涵、目标、手段和内容上均有很大变化[1]。作者提出将模糊聚类分析方法应用于新一轮土地整治规划编制工作中，并根据广元市利州区2010年土地利用状况和社会经济情况，对土地整治进行了分区，本文从数学原理、计算步骤、实际应用等方面加以阐述。

1 模糊聚类方法概述

聚类分析[5-8]是指对事物按一定要求进行分类的数学方法，它是多元统计分析方法之一。但是客观事物之间并没有一个截然区别的界限，分类时所依据的数据指标的变化也大多具有连续性，因此，采用模糊数学方法解决聚类问题必然会更符合实际情况。模糊聚类分析方法给出的结果不是说事物绝对地属于或不属于某一类，而是指明在一定程度上属于哪一类。

1.1 模糊聚类法数学原理

设样本集X={x1,x2, …,xn}中的元素有m个特征，即

xi=(xi1,xi2, …,xim)

欲把X分成c类(2≤c≤n)

构造泛函

(1)

其中uik∈{0,1}。

为第i类的聚类中心。

(2)

为样本xk与聚类中心vi的欧式距离。

1.2 模糊聚类分析方法的计算步骤

模糊聚类分析的主要思想是利用事物的相似性尺度来衡量事物间的远近程度，以此来实现事物的分类。该方法的本质是根据对象本身的属性来构建模糊矩阵，再根据给定的隶属度来确定事物分类的关系[5-8]。

1.2.1 确定分类对象

设有n个待分类的样品，每个样品由m个指标来表述，则数据矩阵表示如下

1.2.2 数据标准化

由于指标之间具有不同量纲和不同数量级，直接利用原始数据分类，就会降低甚至排除某些数量级很小的指标作用，故需要对数据进行标准化处理，使每一种指标统一于某种共同的数据特性范围[5-8]。一般采用标准差标准化的方法来进行。其计算公式为

(3)

其中

河南省南阳市内乡县的一个县衙，挂着一副对联。上联：“穿百姓衣，吃百姓饭。莫以百姓可欺，自己也是百姓。”下联：“得一官不荣，失一官不辱，勿说一官无用，地方全靠一官。”对联既告诫为官者要淡化“官本位”，以勤政为己任，不要忘了自己也是百姓。此联为康熙十九年内乡县知县高以永撰写，挂在内乡县衙三堂。

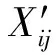
1.2.3 构建模糊相似矩阵

模糊相似矩阵R是衡量样本间相似程度的一种模糊度量方法[5-8]。

相似系数的计算公式为

(4)

其中，c∈0≤rij≤1的一个常数(i,j=1,2,…,n)。

1.2.4 构造模糊等价矩阵

一般情况下，我们对事物进行分类时，必须构造一个模糊等价关系矩阵；但是，模糊相似矩阵仅满足自反性和对称性，不满足传递性，为此需要对相似矩阵进行改造[5-8]。改造的方法是模糊关系矩阵自乘：R∘R=R2，R2∘R2=R4,…,如此下去，直到出现Rk=R2k,则Rk就是一个模糊矩阵t(R)。

1.2.5 聚类分析

得到模糊等价关系t(R)后，就可以在适当水平α上截取t(R),使得模糊等价关系中大于值α的样本归为一类。

2 实际应用

2.1 研究区概况

四川省广元市利州区东邻旺苍县，南连剑阁县、元坝区，西接青川县，北接朝天区。利州区地处龙门山、米仓山和川北丘陵的过渡地带，地势东北、西北高，中部低，南部高；形成北部中山区，中部河谷浅丘及平坝区，南部低山丘陵区的特殊地理环境。区内矿产资源已发现矿种20个，其中探明资源储量的矿种有12个，煤、水泥灰岩和石英砂岩等主要矿种的资源储量较大。

全区现辖原东坝、河西2个办事处、7个镇和3个乡，面积1 533.76 km2，总人口477 612人，其中非农业人口288 582人。全区耕地面积为22 476.15 hm2，占土地总面积的14.65%;全区园地面积共2 659.23 hm2，占土地总面积的1.73%；全区林地面积共105 873.15 hm2，占土地总面积的69.03%；全区草地面积2 035.89 hm2，占土地总面积的1.33%。全区没有天然牧草地和人工牧草地。城镇村及工矿用地占土地总面积的5.13%，交通运输用地占土地总面积的6.38%，水域及水利设施用地占土地总面积的3.73%，其他土地占土地总面积的3.16%。

2.2 指标构建

根据利州区2010年土地利用状况和社会经济数据，构建了10个乡镇的13个主要指标的原始数据，如表1所示。

2.3 样本数据标准化

先计算各个指标的均值和标准差，再由公式(3)得到标准化数据矩阵如表2所示。

2.4 建立模糊等价矩阵

根据构造模糊等价矩阵的原理，当k=4时，出现了Rk=R4k。因此得到模糊等价矩阵t(R)，如表3所示。

2.5 求取模糊相似矩阵

令c=1/max(r11,r12, …,rnn)，通过公式(4)计算得到模糊相似矩阵R,如表4所示。

2.6 取不同值进行聚类

在模糊等价矩阵中， 求取不同的α(0≤α≤1)水平的截距阵。当α=0.7时，得到模糊矩阵的水平截矩阵如表5所示。

表1 广元市利州区各乡镇土地利用和社会经济数据一览表Table 1 Land utilization and socioeconomic data from some small towns of the Guangyuan Lizhou district

1.白朝乡; 2.宝轮镇; 3.赤化镇; 4.大石镇; 5.工农镇; 6.金洞乡; 7.龙潭乡; 8.盘龙镇; 9.荣山镇; 10.三堆镇。 A～H.分别表示耕地、园地、林地、草地、城镇村及工矿用地、交通运输用地、水域及水利设施用地、其他土地占土地总面积的比例; I.坡度指数; J.复垦新增耕地面积(公顷); K.人均土地(亩); L.亩产粮食(千克); M.平均田坎系数。

表2 标准化数据矩阵Table 2 Standardization of the data matrix

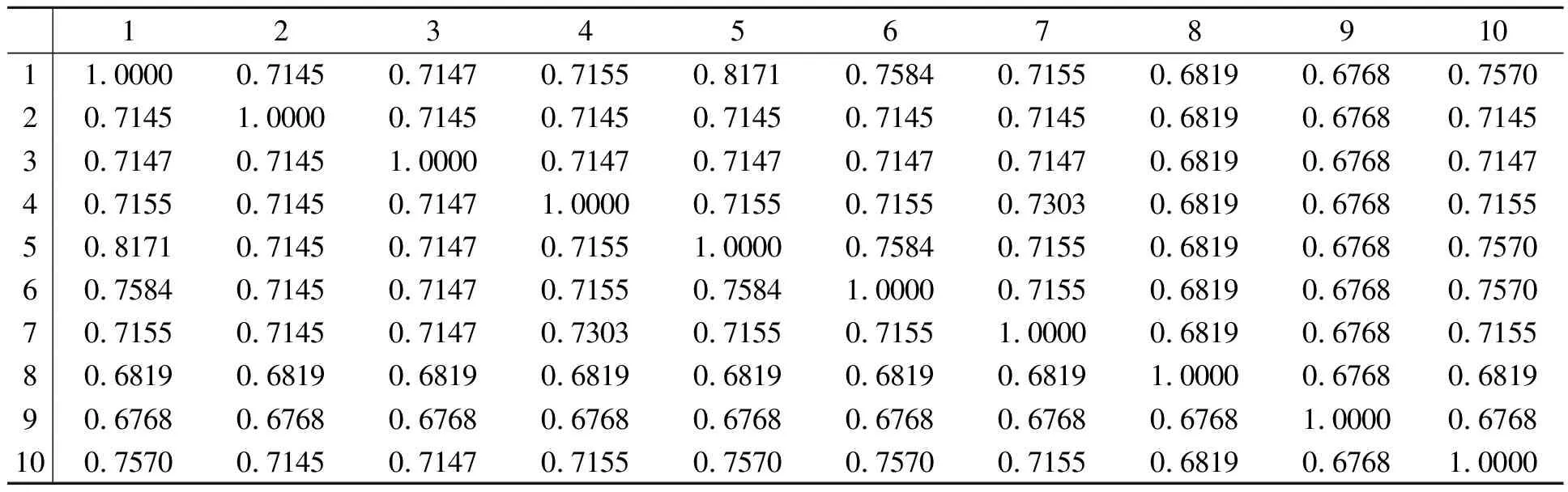
表3 模糊相似矩阵t(R)Table 3 Fuzzy similar matrix t(R)

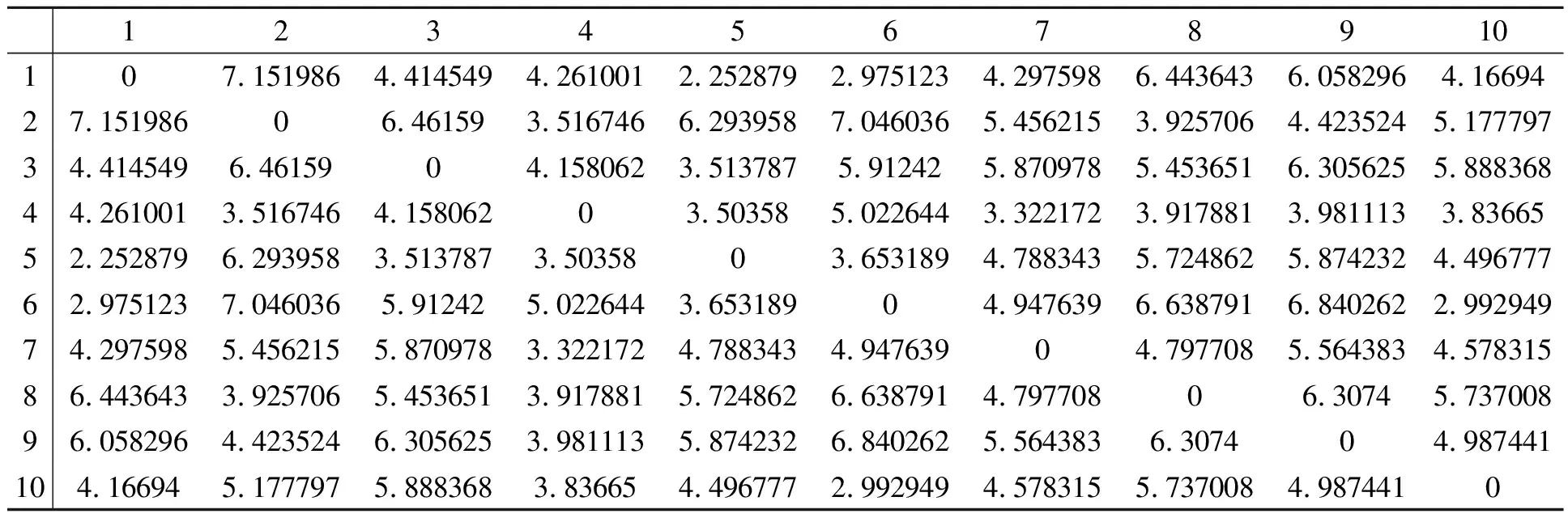
表4 模糊相似矩阵(R)Table 4 Fuzzy similar matrix (R)

表5 模糊等价矩阵的截矩阵Table 5 Cutting matrix of fuzzy equivalence matrix

3 分类结果分析

从表5可得：当α=0.7时，土地整治分区可以分为3类。第一类丘陵整治区{1, 2, 3, 4, 5, 6, 7, 10}、第二类平原整治区{8}、第三类深丘整治区{9}。对应的乡镇分类是：{ 白朝乡, 宝轮镇, 赤化镇, 大石镇, 工农镇, 金洞乡, 龙潭乡, 三堆镇 }、{盘龙镇}、{荣山镇}。模糊聚类分析结果与实际情况结合，结果与事实相符合，从而为土地整治潜力计算以及重点整治区域和方向的布局奠定了很好的基础，这样更有利于因地制宜制订比较科学合理的规划。

4 结论与认识

模糊聚类分析方法在社会、经济、管理等领域方面的应用均取得令人满意的结果，本文提出将模糊聚类分析算法应用于土地整治分区工作中，进一步拓宽了该算法的应用范围。在研究中，得到如下认识：(1)采用模糊聚类分析来进行对象的分类，分类结果与构建科学实际的指标体系有着密切的联系；(2)给定阈值大小对对象分类影响也比较大；(3)为了提高事物分类的科学性和有效性，将神经网络算法融入模糊聚类算法中也是必要的尝试。

[参考文献]

[1] 贾文涛.土地整治有了新目标——《全国土地整治规划(2011—2015年)》解读[J].中国土地，2012(4)：12-14.

Jia W T. Land consolidation has a new goal: “The National Land Planning (2011-2015)” reading[J]. China Land, 2012(4): 12-14. (In Chinese)

[2] 毛美桥,许庆福,丁喜莲,等.新一轮土地整治规划分区研究——以山东省肥城市为例[J].山东国土资源，2012，28(8)：61-64.

Mao M Q, Xu Q F, Ding X L,etal. Study on planning and zoning of new round land remediation: Setting Feicheng City in Shandong Province as an example[J]. Land and Resources in Shandong Province, 2012, 28(8): 61-64. (In Chinese)

[3] 巫晓东.我国土地利用分区研究进展及方法研究[J].科技信息，2011(3)：10376-10380.

Wu X D. Research progress and methods of land use zoning research in China [J]. Science and Technology Information, 2011(3): 10376-10380. (In Chinese)

[4] 王虚,张正雄,李学明,等.聚类分析在土地利用分区中的应用[J].安徽农业科学，1995，23(4)：360-362.

Wang X, Zhang Z W, Li X M,etal. Application of assembling analysis to land use area division[J]. Journal of Anhui Agricultural Sciences, 1995, 23(4): 360-362. (In Chinese)

[5] 谢季坚,刘承平.模糊数学方法及其应用[M].武汉: 华中科技大学出版社,2001.

Xie J J, Liu C P. Fuzzy Mathematics Method and Its Application[M]. Wuhan: Huazhong University of Science and Technology Press, 2001. (In Chinese)

[6] 许永安,徐恒玉.用Excel实现模糊聚类分析[J].安徽农业科学，2005，33(4)：740-742.

Xu Y A, Xu H Y. Fuzzy c1uster analysis with Excel[J]. Journal of Anhui Agricultural Sciences, 2005, 33(4): 740-742. (In Chinese)

[7] 李金云.基于模糊聚类分析法的读者满意度测评研究[J].情报探索，2009(5)：7-10.

Li J Y. Readers’ satisfaction measurement based on Fuzzy clustering analysis [J]. Information Research, 2009(5): 7-10. (In Chinese)

[8] 胡小云,严伍琼.基于Excel的火炮射击精度模糊聚类分析[J].火炮发射与控制学报，2008(4)：21-24.

Hu X Y, Yan W Q. Fuzzy clustering analysis of gun firing accuracy based on Excel [J]. Journal of Gun Launch & Control, 2008(4): 21-24. (In Chinese)