多卫星系统最小可探测偏差仿真分析
王 睿,任 超,戴 鑫,郑 浩,蔡欣恩
(桂林理工大学测绘地理信息学院,广西 桂林 541004)
0 引 言
随着卫星导航技术的飞速发展,美国GPS现代化的实施,俄罗斯GLONASS的更新升级、欧洲GALILEO的逐步建设,我国自主研发的北斗异军突起,全球卫星导航定位系统(GNSS)正逐渐呈现出一种多极竞争与优势互补的崭新局面。传统的依赖于某单一系统进行导航定位已无法很好的消除所产生的缺陷、提高定位精度和可靠性,因此GNSS多系统集成导航定位技术应运而生,多系统融合时代正在逐渐形成[1]。
最小可探测偏差(MDB)是用于描述卫星导航定位系统可靠性的一个内部指标,它代表的是最小可能观测误差[2]。MDB值越大,则可靠性越低,MDB值越小,可靠性越高。GPS是目前最完善、定位精度最高的全球定位导航系统。而我国的北斗二代卫星定位导航系统,虽然在精度方面还有待提高,但是自主系统,高强度加密设计,安全性、可靠性、稳定性,适合关键部门应用[3]。本文对北斗和GPS,以及两者的组合系统进行性能仿真比较,分析三者最小可探测偏差(MDB)值,分析比较三系统可靠性。
1 可见性及最小可探测偏差
1.1 卫星可见性
卫星的可见性是指在特定的仰角下,地面某个观测点在某个时刻能够观测到卫星的数量,或者是在地面某个观测点在某个时段内,所观测的卫星跟踪弧度段的长度。通过对卫星导航系统仿真卫星可见性,不仅能够判断地面某观测站的观测条件,还能对该卫星系统的卫星情况有所了解。影响卫星可见性的因素除了与观测站所处的环境有关外,还与卫星高度角以及观测时间段有联系。
将观测点P1所在的地平线与观测点在最差观测环境下能够观测到卫星的视线方向之间的夹角定为α,如图1所示。S为卫星,O为地球质心,S′为卫星S在地球上的投影点,R为地球半径,h为卫星高度,那么卫星覆盖角d=∠SOP1[4]:

图1 单颗卫星的可见性
1.2 最小可探测偏差
内部可靠性是考察卫星导航定位系统数据质量的重要因素之一。系统的内部可靠性可以通过MDB值来表现,MDB值代表了能以概率γ发现模型误差大小的能力,是检验内部可靠性的重要指标。通过适当的校验统计,MDB值可以用来探测模型误差的大小[5]。设原假设为H0,备选假设为Ha:
H0:E{y}=Ax,D{y}=Qy
Ha:E{y}=Ax+c▽,D{y}=Qy,
(1)
式中:E{·}和D{·}分别为期望和方差;y为观测向量,单位为 m;x为n维的未知向量;A为m×n的设计矩阵;c为已知m维向量的模型误差; ▽为未知模型误差。
H0和Ha比值的均匀最佳检验统计为
(2)
检验统计量T满足以下性质:
H0:T~χ2(1,0) ;Ha:T~χ2(1,λ).
(3)
其中,λ为非中心参数,定义为
(4)
当参数λ0=λ(α0,γ0)(其中a0和γ0分别为置信区间的上下限)已知时,就能检测相应的方差值,也就是MDB值,则由式(4)可得
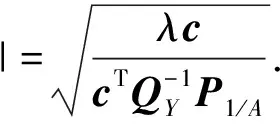
(5)
由此可见,MDB值不但取决于置信区间的上下限,而且和设计矩阵A和协方差矩阵Qy有关。备选假设Ha是用来描述向量c,在GNSS的应用中,备选假设Ha通常与伪距观测和相位观测的异常值和周跳有关。α0和γ0参考值分别为α0=0.001,γ0=0.80,因此可得λ0=17.075.
根据文献[6],不同差分模型下的MDB值表现也不同。几何距离无关模型(简称GF模型)下的MDB值最大,因此该模型检验粗差的能力也是最低的、效果也是最不明显的。而动态接收机模型与静态接收机模型,两种模型下的MDB值是相同的,这说明了,模型的使用与接收机的状态无关,并不会影响MDB值。
2 GPS、COMPASS以及GPS & COMPASS组合系统的仿真
对于全球框架下的GPS和北斗,可以认为GPS的星座有24颗卫星,而北斗有卫星为16颗。本文通过对三个系统的单点定位进行仿真,对比三者可靠性。
2.1 仿真条件
GPS卫星系统的24颗中轨道卫星处于6个平面,每个平面4颗卫星,轨道倾角i=55°;偏心率e=0;轨道面半长轴a=26 560 km[7].北斗的星座的卫星参数为:长半轴a=27 861 km; 轨道倾角为i=55°;椭圆扁率为e=0;近地点角距为ω=0;3个轨道的升交点赤经分别为60°,180°,300°[8].
对GPS和北斗进行仿真时,均选取自由几何模型,接收机状态为静止,时间间隔为300 s,截止高度角为15°,定义相位观测值L1和L2的均方差都为0.003,码观测值L1和L2的标准偏差均为0.3,电离层固定。对于两者的组合系统,对其进行仿真时,相位观测值L1和E1的均方差分别为0.002和0.005,相位观测值L2和E2的均方差分别为0.001和0.006,码观测值L1和E1的标准偏差分别为0.3和0.7,码观测值L2和E2的标准偏差分别为0.3和0.7,其他参数均与两个单系统仿真参数相同。仿真经纬度选取的是北京市区经纬度:北纬39.9°,东经116. 3°.
2.2 结果分析
三系统的卫星可见数如图2所示。

图2 北京地区三系统卫星数比较
从图2中可以看出,北斗在北京地区的可见卫星数均在6至10颗,保证了观测所需的最少卫星数4颗,GPS在北京地区的卫星可见数则没有北斗那么稳定,虽然卫星可见数最大值达到了13颗,但仍然出现了可见卫星只有四颗的情况。组合系统则显示的卫星可见数则要好的许多,最少可见数为9颗,最多时可达到19颗。卫星可见数的增加保证了定位盲点的概率有所降低,提高发现和排除故障卫星的能力。如图3示出了北京地区三系统MDB值的仿真结果图。

图3 北京地区三系统MDB值比较
由图3可知,三系统MDB值仿真结果显示,在北京地区,GPS的MDB值只有在80~100历元时起伏波动较大,在230~250历元时也达到了最小值,这与相应时段内卫星数有关;而北斗在北京地区的MDB值的波动比较大,通过表1可以看出,最大最小值均比GPS要高;组合系统的MDB值显示,相较于单系统而言,组合系统的MDB波动性不大,较为理想。

表1 三系统MDB值比较
表1示出的是三系统仿真MDB值中最大、最小以及均值比较。由于观测卫星数的问题会导致北斗MDB值最大达到了0.032 0,三者的最小值也相差不大。对比三者的均值可见,组合系统的可靠性比单系统的要高。
3 结束语
通过比较三个系统的MDB值可以看出,组合系统的可靠性要比单系统的可靠性要高,在亚太地区,北斗的可靠性要比GPS的可靠性要高。北斗系统作为一种新的卫星导航定位系统,虽然起步时间相对较晚,仍然存在着许多应用方面的缺陷,在很多领域的用途还未被认知,但自主发展卫星导航定位系统在军事上有着重要的意义,并且能够摆脱对国外卫星导航系统的完全依赖。北斗在中国及周边地区的优势要比GPS明显,因此与GPS的组合定位导航可以弥补北斗在其他区域精度方面的不足,提高可靠性。
[1] 郭 斐,张小红,王明华.GNSS多系统集成兼容性问题[J].测绘信息与工程,2008,33(4):13-15.
[2] 赵春梅,欧吉坤,袁运斌.基于单点定位模型的GALILEO及GPS-GALILEO组合系统的定位精度和可靠性的仿真分析[J].科学通报,2005,50(8):811-819.
[3] 龚佩佩,郑 恒,杨卓鹏,等.全球卫星导航系统性能标准以及指标体系概述[C]//第四届中国卫星导航学术年会电子文集,2013.
[4] 于兴旺,张晓红,邰 贺,等.GPS/GLONASS组合单点定位在导航中的应用[J].测绘信息与工程,2001,32(6):1-3.
[5] OU Jikun , WANG Zhenjie. An improved regularization method to resolve integer ambiguity in rapid positioning using single frequency GPS receivers[J].Chinese Science Bulletin,2004,49(2):196-200.
[6] 梁 珺,楚 亮.GPS码观测的最小可探测偏差研究[J].山西建筑,2010,36(6):351-352.
[7] 于清德,吴雨航,陈秀万,等.GNSS几何性能仿真分析[J].计算机仿真,2010,27(6):87-92.
[8] 北斗/GPS双模CORS网研制与测试技术研究[D].上海:上海交通大学,2013.

