GPS高程异常拟合研究及精度分析
闫建伟 ,周长江
(1.铁道第三勘察设计院集团有限公司,天津 300142;2.中国矿业大学环境与测绘学院,江苏 徐州 221116)
0 引 言
GPS测量具有精度高、实时、快速等优点,广泛用于工程测量、变形监测等领域,且平面定位精度已经很高,但GPS高程由于精度不高并没有在生产中得到广泛的应用。传统的水准测量方法,需要耗费大量的人力、物力,效率很低。GPS高程现代化就是在这种背景下由美国大地测量局为代表提出,其核心思想就是要用GPS高程代替传统的水准测量方法。GPS高程是以参考椭球为基准的大地高,而生产常用的是以似大地水准面为基准的正常高,这两者之间的差值叫做高程异常,若能求出高精度的高程异常值就可以求出正常高H.多项式拟合、基于BP人工神经网络的方法是高程拟合模型中用得比较多的方法。
1 正交多项式拟合法
假设对于某区域测了一些离散的点,这些点的大地高HG和正常高H是已知的,就可以得到这些点的高程异常。
ζ=HG-H.
(1)
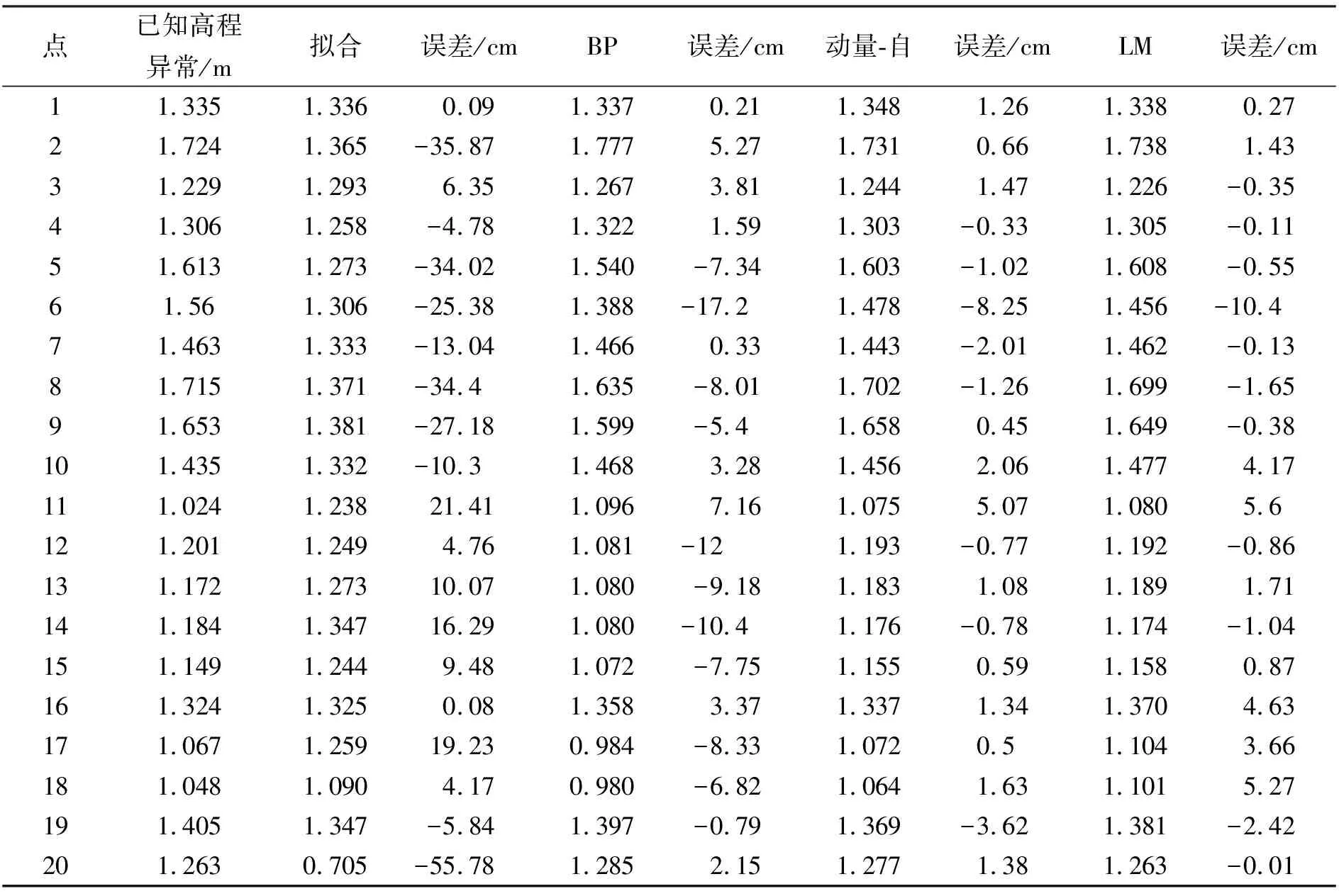
当有n+1个已知点时就可以拟合一个m次(m (2) 其中x为已知点到参考点的距离,一般认为是已知点到测区坐标平均值的直线距离。由于上述多项式的系数矩阵往往是病态的,矩阵的敏感度非常大,对求解不利。若可以构造一组多项式系数Qj(x) (j=0,1,2……m),而这组系数是不大于m且在给定点上是正交的函数,则可以先用Qj(x)作为基函数进行最小二乘拟合为 ζm=q0Q0(x)+q1Q1(x)+……qmQm(x), (3) 系数 (4) 把qj代入到式(3)中,并将其化为一般多项式式(2)的形式。在构造点上的正交多项式Qj(x)的递推公式如下: Q0(x)=1 Q1(x)=x-a0 Qj+1(x)=(x-aj)Qj(x)-βjQj-1(x), j=0,1,2……m-1, (5) 根据以上各式求出高程异常ζ关于x的多项式,则就可以通过未知点的坐标插值出测区其它点的高程异常值,再根据对应点的大地高求出正常高。 (6) 神经网络通过对已知部分样本数据进行学习训练,不断的比较网络输出和实际输出的差值,不断反向调整隐含层和输入层间的权值使误差达到最小,从而不断逼近目标函数。当网络训练学习达到既定的精度要求时,就可以对实验数据进行一个预测,也就是仿真,这就是BP神经网络的的工作原理。 在用BP神经网络进行GPS高程异常拟合时,网络输入为已知点的平面坐标P(x,y),输出为已知点的高程异常ζ,即建立如下的非线性的映射关系。 ζ=f(x,y). (7) 标准的BP算法原理简单,但是收敛速度很慢容易陷入局部极值点,因为BP算法是以梯度下降为基础的,只具有线性收敛速度,并且BP网络算法是一个非线性的优化问题,这就不可避免存在局部极小问题。为了解决这些问题,附加动量的BP网络通过引入一个动量因子mc(0≤mc≤1),不仅考虑误差在梯度上的影响,还考虑误差曲面上变化趋势的影响,从而使误差向着误差曲面底部的平均方向变化。 BP神经网络是一种竞争性神经网络,网络中权值的调整与学习速率和梯度有很大关系。当网络中权值调整降低了误差函数时,说明学习速率变小了,需要增加学习速率的值。而当网络中权值调整没有降低误差函数时,说明速率偏大,应该减小学习速率的值。总之,学习速率应该是动态变化的。但是标准BP网络中学习速率是不变的,因此有人提出了改进的BP算法,即自适应学习速率调整法,让学习速率随网络的训练状态动态调整其值大小。通过将附加动量和自适应学习速率调整结合起来可以大大加快收敛速度,并极大提高转换精度。 标准BP算法中仅利用了目标函数的一阶导数信息,没有利用目标函数的二阶导数信息对网络训练精度进行改进。Levenberg-Marquardt算法弥补了这一缺点,通过利用目标函数的二阶信息构成了一种超线性收敛的方法。这种方法是以非线性优化理论为基础,将BP多层网的训练问题归结为一个非线性的规划问题。但这种算法也带来了一些实际问题,BP多层网是一种并行处理结构,要采用这种算法,必须将网络的权值展开以构成一个权向量来进行各种向量或矩阵运算,这对与多层网的并行处理有较大的影响,使运算工作量增加。 根据上述原理采用matlab编制相应的程序对实验数据进行实验并分析实验精度。实验数据选自某地区联测了水准的54个点,这些点的正常高和大地高都已经知道,因此可以求出它们的高程异常。将这些已知数据分为两组,一组34个点作为已知点进行拟合,在神经网络算法中作为学习样本进行网络训练。另一组20个点作为检验点进行误差检验和精度评定。这些GPS点点位分布情况和高程异常值如图1所示。 图1 已知数据点位分布情况和高程异常 简单的BP神经网络只有2层,即隐含层和输出层。其中隐含层的层数确定目前还没有成熟的理论。在编制matlab程序时,把隐含层设为一层,神经元个数为5个。网络输入为样本点的x、y坐标,输出为相应点的高程异常,即建立一个2×5×1的BP神经网络。在Matlab程序中,需要对网络某些参数赋初值。在标准BP算法中,把最大学习次数设为12 000,目标误差为0.001,附加动量因子mc=0.9,学习速率取为0.8.程序运行后检验点的预测高程异常和与已知值的误差结果如表1所示(其中误差的单位为cm,高程异常的单位为m): 表1 检验点的预测高程异常和与已知值的误差 从表1中可以看出,正交多项式拟合法误差很大,标准BP算法误差要小于正交多项式拟合法,但是误差也比较大,在改进的BP算法中,LM算法误差和附加动量的自适应学习速率调整方法误差相比前两种方法有很大提高。 GPS高程异常拟合的精度评价应有内符合精度和外符合精度两部分组成。内符合精度是算法的内在残差。将参与拟合的34个已知点代入到算法中求出其预测高程异常值ζ与已知值ζ差值,则其残差为V=ζ′-ζ,则内符合精度为 (8) 外符合精度指模型的外推精度,通过检验模型拟合值与已知值的误差大小可以了解模型与目标值的逼近情况。实验中将20个检验点代入到程序中求出其拟合高程异常ζ′与其已知的值的ζ差值,则其误差为V=ζ′-ζ.则外符合精度为 (9) 求出这几种方法的内外符合中误差,并绘制出不同算法的内在和外推残差曲线,由于正交多项式法误差较大,在此仅绘出标准BP神经、附加动量的自适应算法、Levenberg-Marquardt算法的误差曲线,结果如表2和图2、图3所示。 表2 几种算法的内外符合精度 图2 三种模型检核点内残差对比 图3 三种模型外检核残差对比 从以上实验结果可以看出,正交多项式拟合法只能达到分米级精度,精度远不如标准BP神经网络。标准BP神经网络在精度上较多项式拟合法有很大改善,但是收敛速度很慢,需要迭代将近1 000次才能达到目标误差,拟合后的残差也比较大。在改进的BP算法中,附加动量的自适应方法和Levenberg-Marguardt方法在网络预测方面均优于标准BP神经网络,其中Levenberg-Marguardt收敛速度最快,通过几十次迭代就可达到目标误差。对于这两种模型来说,附加动量的自适应法精度上要略优于LM算法,在实际应用过程中要结合具体实例,当已知的学习训练样本数据比较多时,为了达到较高的精度,宜选用Levenberg-Marguardt法。当样本数据比较少时,选择附加动量的自适应方法。 GPS高程转换方法有多种,每种方法针对不同的拟合数据都有其优缺点,在进行应用时要结合测区实际情况选取适合的方法进行计算。本文主要针对多项式拟合和BP 神经网络及其改进算法进行了论述,并结合具体项目数据进行实验,对比不同方法的拟合精度,分析了各个方法针对本区域的适用情况,由于文中所选的已知数据是通过GPS处理软件后处理得到,部分已知数据存在粗差,个别点拟合后精度不是很高。在实际应用中,应尽量选用精度较高的已知数据,这对提高GPS高程转换精度有很大帮助。 [1] 丛 爽.面向MATLAB工具箱的神经网络理论与应用[M].合肥:中国科学技术大学出版社,1998. [2] 鲁铁定,周世键等.关于BP神经网络转换GPS高程的若干问题[J].测绘通报,2003,(8):7-9. [3] 沈学标.GPS水准高程拟合精度的分析[J].测绘通报,1998,44(7):21-22. [4] 胡伍生,华锡生,张志伟,等.平坦地区转换GPS高程的混合转换方法[J].测绘学报,2002,31(2):128-133. [5] 魏子卿.高程现代化问题[J].武汉大学学报·信息科学版,200l(5):377-380.
2 基于BP人工神经网络GPS高程拟合方法
2.1 标准BP神经网络
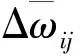
2.2 附有动量的自适应学习速率调整法
2.3 Levenberg-Marquardt算法
3 实例计算

4 精度分析
4.1 内符合精度
4.2 外符合精度
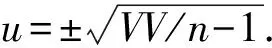



5 结束语

