非均匀介质在动荷载作用下的裂缝扩展研究

，，，

(大连理工大学 土木工程学院，辽宁 大连 116024)

1 研究背景

随着采油工程、采矿工程、地下工程和防护工程的发展，岩石等非均匀材料的动力特性在理论研究和工程应用中越来越受到重视。岩石作为一种非均匀脆性介质，其内部常分布大量的节理、裂隙等各种裂纹缺陷，这些原始裂纹缺陷在外部荷载作用下扩展、延伸和贯通，导致岩石的宏观变形与破裂。相关研究包括：刘磊等[1]采用自编有限元程序对含不同预置角度穿透裂纹板受动态拉伸荷载进行了数值模拟，研究了不同幅值载荷和预置裂纹角度对裂纹扩展的影响；黄凯珠等[2]研究了双轴作用下不同几何分布和不同围压的断续预置三裂纹的萌生、扩展和贯通机制；杨圣奇等[3]基于试验结果研究了不同围压下断续预制裂纹粗晶大理岩的变形和强度特性；J.S.Hawong等[4]采用Homalite-100模型试样，研究了岩石类脆性材料在动态双轴加载情况下的裂纹扩展问题。由于岩石具有明显的非弹性、各向异性、不连续性和多节理裂隙性等特点，在考虑惯性效应情况下，作为理论基础的应力波理论必须作出特定的限制[5]。从断裂力学的角度来看，在应力波与介质中的天然裂纹相互作用时，如果裂纹尖端的应力强度因子K达到材料抵抗动态断裂的韧性指标——断裂韧度Kd(仅对Ⅰ型裂纹而言)时，材料就会开始失稳而产生新的裂纹[6]。由于断裂力学采用连续介质力学方法，对于岩石这种非均匀材料，其结论往往具有局限性，不能很好地揭示岩石在动荷载作用下所表现出的一些重要特征。本文采用RFPA数值模拟工具，用统计损伤的本构关系来描述岩石的非均匀性和缺陷分布的随机性，对预置不同裂纹倾角和岩桥倾角的一组裂纹试样受动态荷载的裂纹扩展方式进行了数值研究。

2 数值模拟模型

本文所用的RFPA-dynamic分析系统，可以模拟动荷载作用下岩石等非均匀脆性材料的破裂过程。有关RFPA-dynamic的详述请参见文献[7-9]。

本文研究预置裂纹倾角、岩桥倾角及双向荷载(不同荷载比率)对裂纹扩展过程的影响。计算模型见图1，模型尺寸为60 mm×80 mm，划分为240×320=76 800个单元。预置裂纹设于试样中部，裂纹长15 mm，宽约1 mm。裂纹倾角α分别为15°，30°，45°，60°,75°，岩桥倾角β分别为25°，45°，75°,90°。施加的动荷载为矩形荷载，加载时间为30 μs，加载幅值如图2所示。

为了考虑材料的非均匀性，假设基质单元的弹性模量及强度等力学参数服从Weibull分布函数，即

(1)

图1 试样几何分布模型

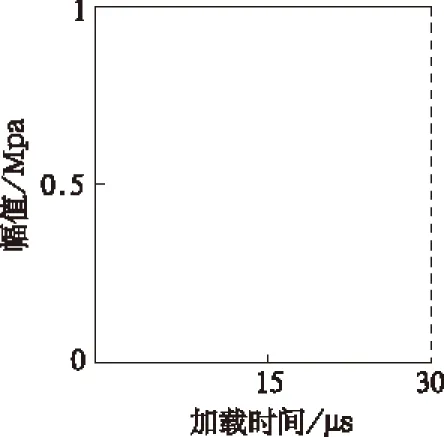
图2 加载曲线

式中：m为形状参数，反映岩石材料力学性质的均质度，m越小表明岩石的性质越不均匀；α0为反映岩石材料平均性质的参数。有关上述分布函数和参数的定义及选取方法参见文献[10-11]。

本文模型中，基质单元平均抗压强度为100 MPa，平均弹性模量为50 GPa，均质度为3，密度为2 500 kg/m3，摩擦角为50°，泊松比为0.25，压拉强度比为10，阻尼系数为0，不考虑阻尼的影响，时间步长为0.1 μs，模型边界为自由边界，采用平面应力分析。

3 计算结果分析

3.1 单向荷载下裂纹倾角和岩桥倾角对裂纹扩展的影响

如图3所示，裂纹倾角α=45°的试样在幅值1 MPa、加载时间30 μs的单向动荷载作用下，裂纹扩展的最大主应力及其局部放大图。从应力图中可看出，当裂纹倾角α=45°时，不同岩桥倾角的岩样有着几乎一样的扩展方式，即大致沿与动荷载垂直的方向扩展，这一结论与文献[1]保持一致。但是不同的岩桥倾角试样在裂纹前缘区域有着不一样的扩展方式，分述如下：

(1)岩桥倾角β=25°和45°时，裂纹尖端之间的垂直距离较小，尖端产生的裂纹沿水平方向扩展时，在裂纹界面上将发生应力波的反射与叠加，继而形成一个压应力集中区(局部放大图中曲线区域)，并随着裂纹的扩展而移动。由于岩石抗压强度明显高于其抗拉强度，所以区域中除了个别低强度单元发生破裂外，不会形成明显的裂纹。由于存在压应力集中区，两裂纹尖端萌发的裂纹不会相互贯通，且延伸较短。

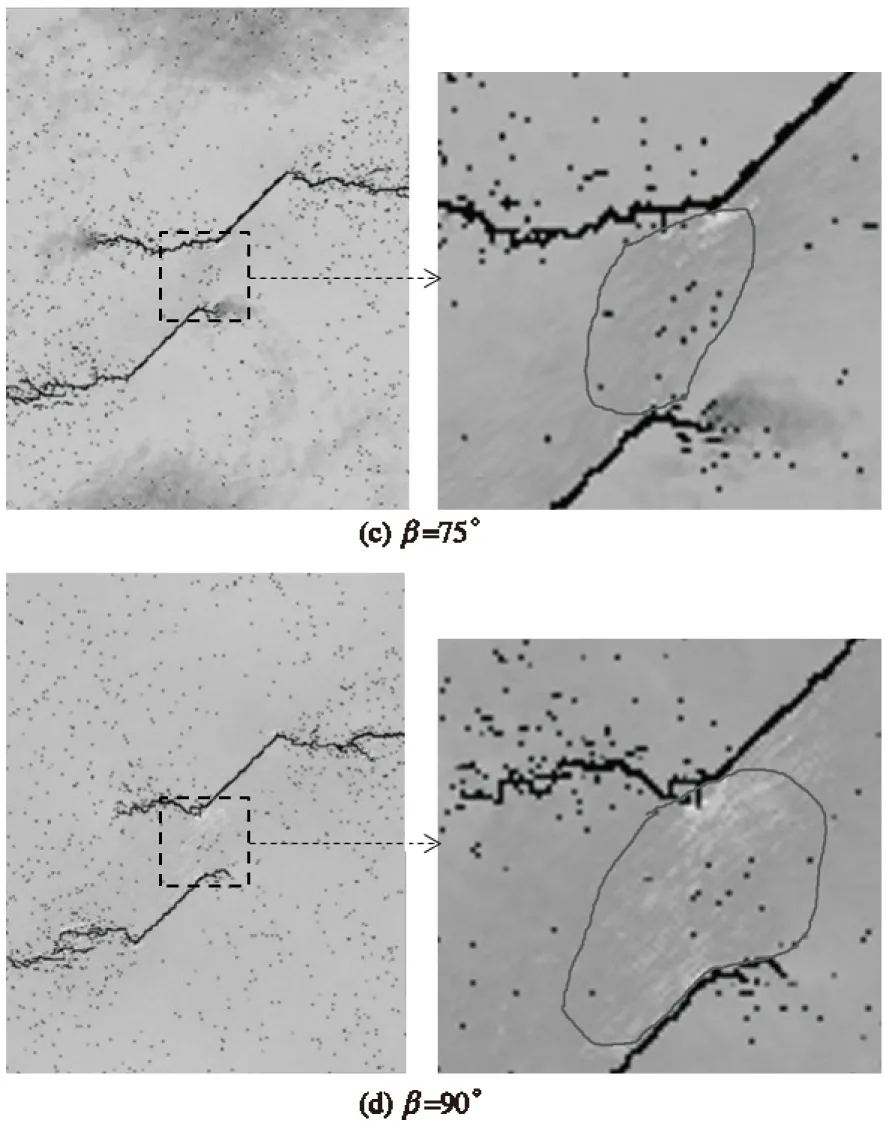
注：应力图的灰度代表应力的高低，越亮应力越大。

(2)岩桥倾角β=75°和90°时，裂纹尖端之间的垂直距离增大，所以形成面积较大、应力集中程度较小的压应力集中区。两裂纹尖端萌发的裂纹，一条延伸较长，另一条延伸较短。

本文还对裂纹倾角α分别为15°，30°，60°,75°，岩桥倾角β分别为25°，45°，75°，90°的试样进行了数值模拟。在岩桥倾角一定条件下，不同裂纹倾角的试样有着几乎一样的扩展方式，即大致沿与动荷载垂直的方向扩展；但随着裂纹倾角的增大，裂纹开始扩展所需的时间增大。在裂纹倾角一定条件下，岩桥倾角对裂纹扩展方式的影响很小，随着岩桥倾角的增大，裂纹尖端的应力集中程度减小。限于篇幅，此处不再给出图形。

笔者在文献[12]中研究了岩石等非均匀介质在静荷载作用下裂纹的扩展方式，同时也讨论了裂纹倾角分别为15°，30°，45°，60°，75°，岩桥倾角分别为25°，45°，75°，90°时裂纹的扩展方式，以及双向荷载对裂纹扩展方式的影响，具体内容请参见原文。与文献[9]对比发现,同样几何分布的裂纹分别在静荷载和动荷载作用下，其扩展方式有着显著的区别。文献[12]中得出的结论是：裂纹几何分布(不同裂纹倾角、不同岩桥倾角)对裂纹贯通机制有显著影响，而本文的研究发现裂纹倾角对裂纹贯通机制几乎没有影响，岩桥倾角的影响也局限在很小的区域内,说明研究岩石等非均匀介质中预制裂纹在动荷载作用下的扩展、延伸和贯通具有重要意义。

如图4所示，裂纹倾角为45°时，不同岩桥倾角的试样在动荷载作用下声发射释放的累积能量随加载时间具有如下特征，即裂纹的扩展大致分为4个阶段：①裂纹未发生变化阶段(O—A段)，声发射释放的累积能量折线接近于水平方向，说明此时只有个别单元出现损伤，发生破裂；②裂纹扩展初始阶段(A—B段)，声发射释放的累积能量折线开始上升，说明裂纹尖端开始产生拉应力集中，当裂纹尖端的等效应力超过最大等效应力极限时，裂纹开始扩展，形成宏观小裂纹，并逐渐沿水平方向延伸；③裂纹扩展加速阶段(B—C段)，声发射释放的累积能量折线急剧上升，裂纹快速扩展，形成宏观大裂纹；④裂纹扩展停止阶段(C—D段)，此阶段声发射释放的累积能量折线又接近于水平方向，此时裂纹已经贯通至边界，由于应力的不断释放，裂纹不再扩展。

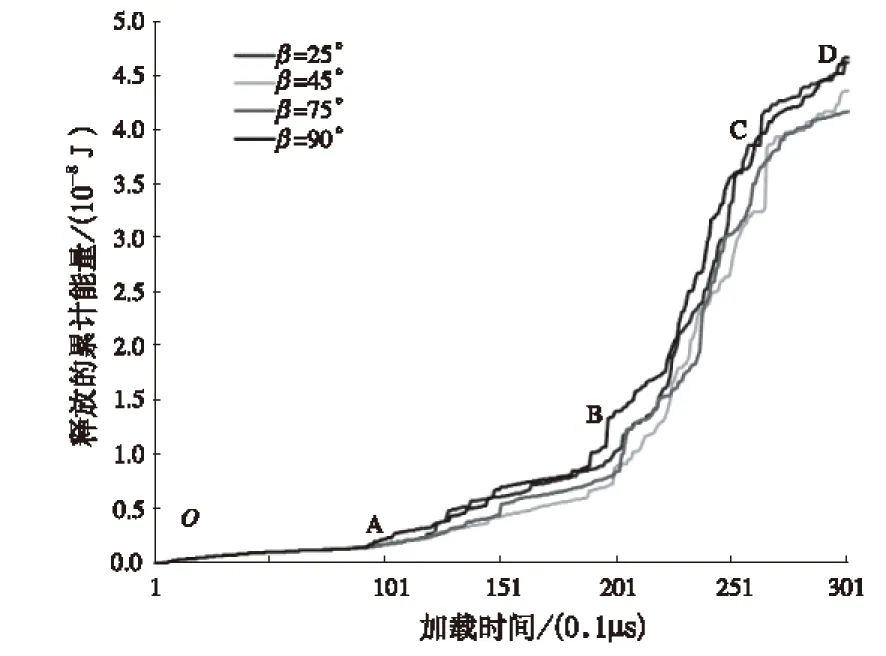
图4 释放的累积能量与加载时间的关系曲线

3.2 特定几何分布下双向荷载对裂纹扩展的影响

在裂纹倾角为45°、岩桥倾角为75°条件下，研究双向荷载(不同荷载比率B=σy/σx)对裂纹扩展的影响。对试样竖直方向施加幅值为1 MPa的矩形荷载，水平方向施加幅值分别为0.4，0.8，1.0，1.2 MPa的矩形荷载，即B分别为2.5，1.25，1，0.83，加载时间均为30 μs。不同荷载比率下的最大主应力见图5。

注：应力图的灰度代表应力的高低，越亮应力越大。

从图5可以明显看出，随着荷载比率B的减小，裂纹的弯曲弧度增大，逐渐偏向于竖直方向，即逐渐与水平荷载垂直(当B=0.83时，σx>σy)，说明双向荷载中较大的荷载对裂纹的扩展方向起主导作用。从弯曲的方向来看，本文的数值结果与图6[4]所示的物理试验结果较吻合。从图5中还可以看出，随着水平荷载的增加，岩桥出现了贯通现象。这是由于在双向荷载下，水平向和竖直向应力波在试样中心，即在裂纹尖端互相叠加，形成了一个拉应力集中区，导致尖端产生的裂纹互相贯通。

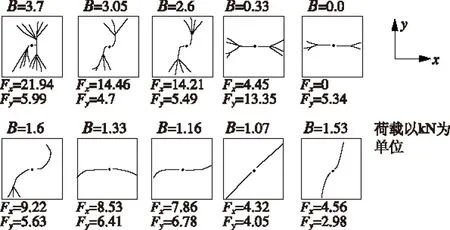
图6 双向拉应力作用下裂纹扩展图[4]

3.3 双向荷载下裂纹倾角和岩桥倾角对裂纹扩展的影响

在一定双向荷载作用下，研究裂纹倾角和岩桥倾角对裂纹扩展的影响。图7为在荷载比率B=1.25和岩桥倾角75°的条件下，不同裂纹倾角试样加载到30 μs时的最大主应力。从应力图可以明显看出，随着裂纹倾角的增大，裂纹扩展方向偏向于竖直方向。但在单向荷载作用下，不同倾角的裂纹试样有着几乎一样的扩展方式。这是由于双向荷载时，应力波在裂纹表面反射，再与入射波叠加后，使得裂纹前缘最大拉应力偏转。

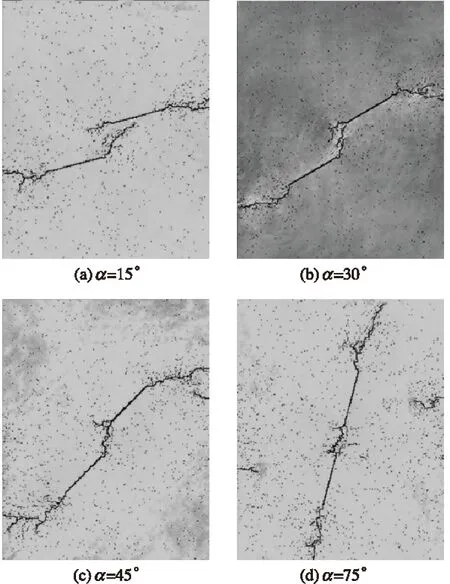
注：应力图的灰度代表应力的高低，越亮应力越大。

笔者还在荷载比率B=1.25和裂纹倾角为45°的情况下，研究了岩桥倾角分别为25°,45°,75°,90°的裂纹扩展方式。模拟结果显示在裂纹倾角一定的情况下，岩桥倾角对裂纹的扩展方式几乎没有影响。限于篇幅，此处不再给出图形。

4 结 论

(1)单向动荷载作用下，裂纹倾角对裂纹扩展方式几乎没有影响，即裂纹大致沿与荷载垂直的方向扩展；岩桥倾角对裂纹扩展方式的影响也是很小的，主要体现在裂纹尖端的应力集中区。

(2)单向动荷载作用下，声发射释放累积能量的过程大致分为4个阶段：裂纹未发生变化阶段、裂纹扩展初始阶段、裂纹扩展加速阶段和裂纹扩展停止阶段。

(3)双向动荷载作用下，不同荷载比率下试样的裂纹扩展方式明显不同，表现在随着荷载比率的减小，裂纹的弯曲弧度增大，逐渐与水平荷载垂直。

(4)双向动荷载作用下，岩桥倾角一定时，随着裂纹倾角的增大，裂纹扩展偏向竖直方向；裂纹倾角一定时，岩桥倾角对裂纹的扩展方式几乎没有影响。

(5) 静荷载与动荷载对裂纹扩展方式的影响主要区别为：单向静荷载作用下，裂纹倾角和岩桥倾角对裂纹扩展方式有显著影响；单向动荷载作用下，却对裂纹扩展方式几乎无影响。 双向静荷载作用下，随着围压的增大，裂纹沿水平方向扩展；双向动荷载作用下，随着荷载比率的减小，裂纹沿竖直方向扩展。

参考文献：

[1] 刘 磊，刘亚东，张亚军，等.含不同角度穿透裂纹板拉伸断裂的有限元模拟[J].中国科学技术大学学报，2012，42(4)：270-279.(LIU Lei，LIU Ya-dong，ZHANG Ya-jun，etal.Response of Elastic-plastic Plate Embedded Cracks at Different Orientation under Impact Load[J].Journal of University of Science and Technology of China，2012，42(4)：270-279.(in Chinese))

[2] 黄凯珠，林 鹏，唐春安，等.双轴加载下断续预置裂纹贯通机制的研究[J].岩石力学与工程学报，2002，21(6)：808-816.(HUANG Kai-zhu，LIN Peng，TANG Chun-an，etal.Mechanisms of Crack Coalescence of Pre-existing Flaws under Biaxial Compression[J].Chinese Journal of Rock Mechanics and Engineering，2002，21(6)：808-816.(in Chinese))

[3] 杨圣奇，温 森，李良权.不同围压下断续预制裂纹粗晶大理岩变形和强度特性的试验研究[J].岩石力学与工程学报，2007，26(8)：1572-1587.(YANG Sheng-qi，WEN Sen，LI Liang-quan.Experimental Study Deformation and Strength Properties of Coarse Marble with Discontinuous Pre-existing Cracks under Different Confining Pressures[J].Chinese Journal of Rock Mechanics and Engineering，2007，26(8)：1572-1587.(in Chinese))

[4] HAWONG J S，KOBAYASHI A S，DADKHAH M S，etal.Dynamic Crack Curving and Branching under Biaxial Loading[J].Experimental Mechanics，1987，27(2)：146-153.

[5] 黄理兴.岩石动力学研究成就与趋势[J].岩土力学，2011，32(10)：2889-2900.(HUANG Li-xing.Development and New Achievements of Rock Dynamics in China[J].Rock and Soil Mechanics，2011，32(10)：2889-2900.(in Chinese))

[6] 黄理兴.动载作用下岩石断裂裂纹的扩展与控制[J].岩土力学，1989，10(1)：54-59.(HUANG Li-xing.Propagation and Control of Crack in Rock Mater under Dynamic Loading[J].Rock and Soil Mechanics，1989，10(1)：54-59.(in Chinese))

[7] CHAU K T，ZHU W C，TANG C A，etal.Numerical Simulations of Failure of Brittle Solids under Dynamic Impact using a New Computer Program-DIFAR[J] .Key Engineering Materials，2004，263(1)：239-244.

[8] ZHU W C，TANG C A，HUANG Z P，etal.A Numerical Study of the Effect of Loading Conditions on the Dynamic Failure of Rock[J].International Journal of Rock Mechanics and Mining Sciences，2004，41(3)：424-424.

[9] ZHU W C，TANG C A.Numerical Simulation of Brazilian Disk rock Failure under Static and Dynamic Loading[J].International Journal of Rock Mechanics and Mining Sciences，2006，43(2)：236-252.

[10] 唐春安.岩石声发射规律数值模拟初探[J].岩石力学与工程学报，1997，16(4)：368-374.(TANG Chun-an.Numerical Simulation of AE in Rock Failure[J].Chinese Journal of Rock Mechanics and Engineering，1997，16(4)：368-374.(in Chinese))

[11] TANG C.Numerical Simulation of Progressive Rock Failure and Associated Seismicity[J].International Journal of Rock Mechanics and Mining Sciences，1997，34(2)：249-261.

[12] 钟波波，张永彬，李 宏.基于RFPA2D的岩石裂纹扩展方式的研究[J].武汉理工大学学报，2014，36(2)：82-88.(ZHONG Bo-bo，ZHANG Yong-bin，LI Hong.Study of Mechanisms of Crack Propagation of Rock Based on RFPA2D[J].Journal of Wuhan University of Technology，2014，36(2)：82-88.(in Chinese))