掺气减蚀设施数值模拟研究探讨

， ，，

(1.中国电建集团贵阳勘测设计研究院 工程勘察分院，贵阳 550000; 2.长江科学院 水力学研究所，武汉 430010)

1 研究背景

随着计算机和计算流体力学的迅猛发展，数值模拟技术以其成本低、信息获取完整、方案变换灵活等优点逐渐成为研究复杂流动问题的有效工具，如邓军等[1]采用VOF模型对泄洪洞进行了数值模拟研究，计算得到了空腔形态、通风设施进气量及挑距等水力参数；刁明军[2]结合κ-ε模型和VOF模型，对龙抬头明流泄洪洞进行了三维紊流数值模拟，并采用插值技术在加密后的网格中插入初算的粗网格的计算成果，获得较高的计算精度;张晓东[3]采用欧拉模型研究了陡槽挑坎掺气水流;覃昕慧[4]采用欧拉模型获得了掺气坎后下游断面的掺气浓度分布;张宏伟等[5]采用欧拉模型对陡槽挑坎的掺气水流进行了二维模拟，在相间作用力本构方程的构建上考虑了湍流扩散的影响，详细研究了相间作用力对挑坎下游掺气浓度分布的影响。

由于掺气水流问题本身的复杂性，在理论研究方面至今也还没有取得突破性进展，而物理模型试验受量测手段、几何比尺和技术等条件的限制，研究时间往往较长，工作量也较大，并且无法避免缩尺效应的影响。对掺气水流进行数值模拟时，都会对相间作用力采用一定的简化假设，因此数值模拟也只能在一定程度上模拟掺气水流。

本文采用fluent流体软件对某泄洪洞及掺气设施水力特性进行了数值模拟，并利用该泄洪洞单体1∶50和1∶30比尺水力学模型试验成果进行了验证。

2 模型试验装置及试验工况

某泄洪洞工作闸门后的无压段采用“龙落尾”型式，截面为“城门洞”形式。城门洞截面为14 m×18 m(宽×高)，侧边墙高14 m，洞顶拱形半径为8.12 m，弧度为118.98°的圆弧。无压段底板曲线分3段：上游段长约为275 m、坡度为0.03的缓坡直线段；中间长约为30 m的曲线连接段，曲线方程为y=0.03x+x2/250；下游长约为122 m、坡度0.268的陡坡直线段。泄洪洞出口采用挑流方式消能，挑流鼻坎高程为860.00 m。鼻坎下游设置人工水垫塘消能，塘底高程790 m。如图1所示。

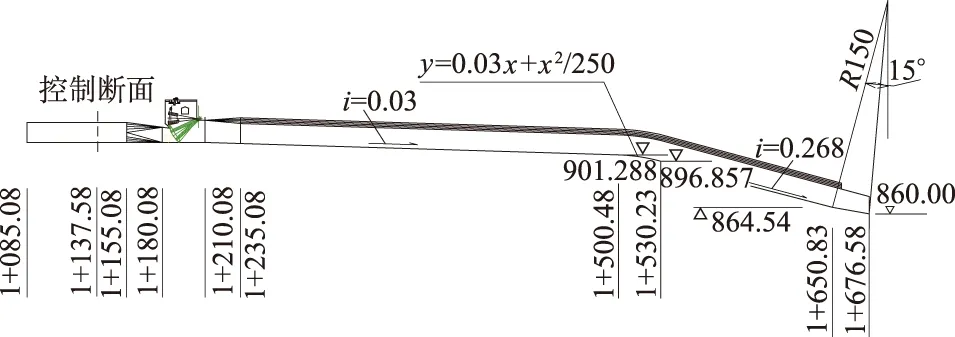
图1 泄洪洞明流段模型的体型布置纵剖面图

该泄洪洞的正常水位泄流量为3 388 m3/s，设计水位泄流量为3 535 m3/s，校核水位泄流量为3 723 m3/s。无压段长度将近500 m，最大流速近40 m/s，高速水流产生空化空蚀的可能性较大，为此在无压段设置了跌坎掺气设施。通气孔直径为1.5 m,为圆形断面孔。如图2所示。

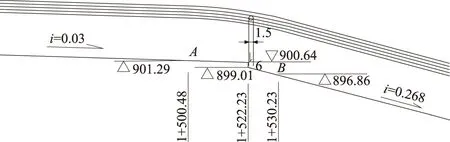
图2 掺气设施体型详图

本文拟采用CFD方法对该泄洪洞的无压段进行数值模拟计算，以便获得与跌坎掺气水流有关的水力特性，并将计算结果与明流段的1∶30单体水工模型试验数据对比。

3 VOF模型

VOF模型[6]假定两相或多相流态之间不发生质量交换，在一个计算单元内，定义了每相流体之间的体积分数，单元内所有流体相的体积分数之和为1。只要知道每一位置、每相流体的体积分数，那么流场内的所有特征参数就可用流体相数和体积分数的平均值来描述。在任一给定的单元上，特征参数代表一相流体还是多相流体，取决于体积分数。如果在一个单元内定义第q相流体的体积分数为αq，则：

αq=0，表示单元内第q相流体不存在；

αq=1，表示单元内只有第q相流体；

0<αq<1，表示单元内存在两相或多相流体之间的交界面。

根据局部的αq值，就可以确定计算域内每一控制体上的特征参数。自由面位置可通过求解多相流体积分数的连续方程来确定。对于第q相流体，其方程形式[6]为：

求解连续方程可跟踪水气界面。对于体积分数方程可以用隐式或显示时间离散格式求解。经过试算，本文对体积分数采用隐式时间离散格式求解。

4 欧拉模型

4.1 体积分数

欧拉模型[6]也称双流体模型，可以模拟多相分离流及相互作用的相，相可以是液体、气体、固体。在多相流模型中，欧拉模型用于流动中的每一相。互相贯穿连续的多相流动的描述组成了相体积分数的概念，表示为αq。体积分数代表了每相所占据的空间，并且每相独自地满足质量和动量守恒定律。

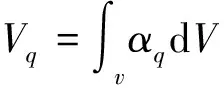
4.2 守恒方程

守恒方程的获得可以使用全体平均每一相的局部瞬态平衡或者使用混合理论方法。在计算中，可以不考虑相变，同时忽略表面张力、假设水气两相均不可压缩、水气界面局部静压平衡，通用的守恒方程形式[7-8]如下：

连续方程

动量方程

4.3 相间质量交换

相间质量交换Γk是由于界面上的相变而引起的向k相的质量传输率。对于水气二相流而言，水气两相间是通过蒸发、凝结、溶解或水中溶解气体的释放来实现质量交换的，在常温常压的情况下，这种质量交换过程与高速掺气水流的空气混掺过程相比，完全可以忽略不计[9]，即Γk=0。

4.4 相间动量交换

根据Ishii[9]的研究，相间动量交换Mk可进而表示为

式中：上标D,L,V,B分别表示静态阻力、升力、虚拟质量力和Basset力。结合文献[5]，在掺气水流中，阻力和虚拟质量力是重要的，本文仅考虑这2种作用力。

5 紊流模型

在标准κ-ε模型中κ和ε是2个基本未知量，与之对应的输运方程[10-11]为：

连续方程

动量方程

κ方程

Gk+Gb-ρε-YM+Sk;

ε方程

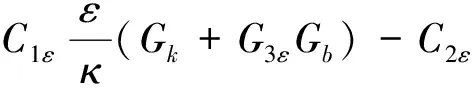
式中：t为时间；ui和xi分别为速度分量和坐标分量；ρ和μ为密度和分子黏性系数；P为修正的压力；Gk是由于平均速度梯度引起的紊动能κ的产生项；Gb是由于浮力引起的紊动能κ的产生项；YM代表可压缩紊流中脉动扩张的贡献；C1ε，C2ε，C3ε为经验常数；σk和σε分别是与紊动能κ和耗散率ε对应的Prandtl数；Sk和Sε是用户定义的源项。对于不可压流体，且不考虑用户自定义的源项时，Gb=0，YM=0，Sk=0，Sε=0。在标准κ-ε模型中，根据Launder等的推荐值及后来的实验验证，模型常数的取值为：C1ε=1.44，C2ε=1.92，C3ε=0.09，σk=1.0，σε=1.3。

选择紊流模型时，一方面要测定其用于各种不同流动时能在不调整其中的常数项前提下以多大精度描述流动，另一方面还要测定其处理问题所需的时间及计算所需的费用，前者对工程应用极为重要。目前在工程中应用最广泛的紊流模型为雷诺时均模型和大涡模拟，雷诺时均模型又以双方程κ-ε模型最为成熟，以雷诺应力模型最为精确。本文选择标准κ-ε模型进行计算。

6 计算方法

6.1 边界条件

计算过程中，入口分为上部空气入口和下部水入口。其中上部空气入口为压力边界条件，为大气压力;下部水入口为由模型率定的入口流量与入口过水断面面积比值计算入口速度，依据计算工况的不同分别取:V正常=25.45 m/s;V设计=26.30 m/s;V校核=27.19 m/s。考虑到实际的水流运动过程在初始状态时通气孔风速和压力均为0，随着掺气的持续进行，风速发生变化，但通气孔入口压力变化不大。故两侧通气孔处均取为大气压力入口。出口边界也是由上部的气体和下部的水组成，水流出口一般较平顺，本文对出口边界采用压力边界条件，为大气压。整个过水道边界都为固壁边界，在固壁边界上取为无滑移边界，对黏性底层采用标准壁面函数处理。

6.2 网格划分

该泄洪洞断面形状为城门洞形，由于洞顶部位为弧线，靠近洞顶的网格质量不好控制。因此，为了简化和网格划分的方便，计算模型用等高的矩形断面代替。经过试算，将泄洪洞往入口方向延伸30.01 m，即将入口断面往上游延伸30.01 m，当水流运动到实际入口断面时，水力特性参数与模型率定的比较接近。

该计算模型全部采用六面体结构化网格，并在掺气坎的上下游局部进行加密，见图3。

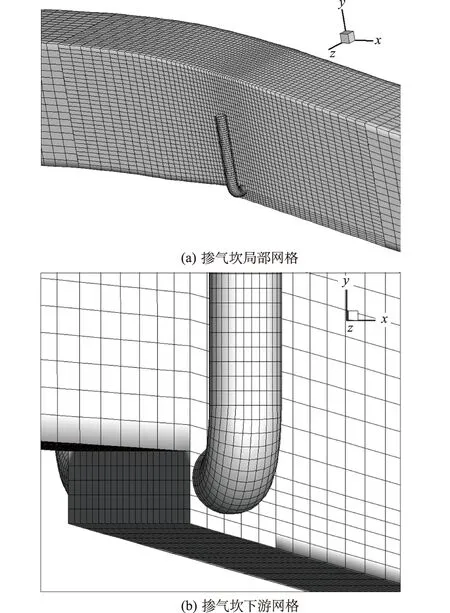
图3 网格划分

6.3 计算方法

采用有限体积法，隐格式迭代求解。根据文献[3]，欧拉模型的气泡直径取为1 mm，其相间动量交换系数采用对称模型[5]，压力校正采用Phase Coupled SIMPLE 方法，其它方程采用QUICK离散格式。VOF模型动量方程的离散采用二阶迎风格式，其它为默认格式。模拟计算采用非恒定流算法逼近恒定流稳定解，时间步长取决于网格尺寸和流速大小，本次计算取0.000 5～0.005 s。

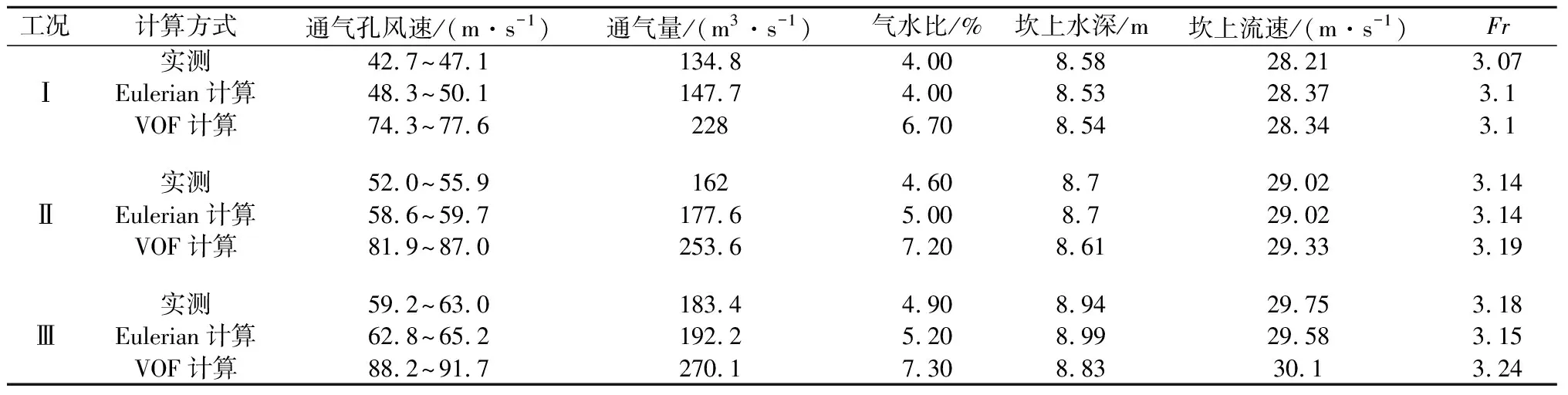
表1 掺气设施的水力特性

7 计算结果与分析

计算过程有3种工况，依次为工况：Ⅰ(Q=3 388 m3/s)，Ⅱ(Q=3 535 m3/s)，Ⅲ(Q=3 723 m3/s)。

7.1 水面线

泄洪洞无压段的水面线见图4、图5。

图4 计算稳定时水面线沿程分布Q=3 535 m3/s

图5 实测水面线与计算水面线比较Q=3 535 m3/s(VOF和Eulerian都比较接近)

计算结果以水相体积分数为0.5的等值面作为水气分界面。从实测水面线与计算水面线比较来看，两者吻合较好。从计算结果可以看出，欧拉模型和VOF模型都能很好地预测水面线的沿程分布。

7.2 掺气坎上水力特性

定义掺气坎后掺气水流的气水比β和掺气坎上水流的弗劳德数Fr为：

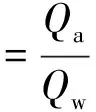
式中：Qa为通气量；Qw为水流量；V为掺气坎上的断面平均流速；h为掺气坎上水深。

从表1可以看出，在对掺气设施的水力特性模拟中，2种计算模型的计算结果与实验值均吻合较好，只是VOF模型计算的通气孔风速明显偏大，其原因可能是VOF模型在描述水气两相间的作用力和运动特性时过于简化。

7.3 空腔特性

此处以Lk表示空腔的长度；Ln表示水舌内缘的挑距。其中空腔长度以水相体积分数为0.5的等值面作为分界面。

从表2可以看出，欧拉法和VOF方法都能在一定程度上预测空腔特性，尤其是水舌内缘挑距与实验值吻合较好。对空腔负压的预测也能和实验值大致吻合。而对空腔长度的计算值均有一定程度的偏大，其原因可能是计算模型中把空气作为不可压缩流体处理，而实际的空腔内是可压缩的水气混合物。再者，实际的掺气水流各相之间的作用力往往比较复杂，而2种计算模型对相间作用力进行估计时都做了不同程度的简化。

表2 掺气坎后形成的空腔特性特征参数

7.4 掺气浓度

实验测量了坎后9个断面在渠底中心线的掺气浓度，因此计算结果也取自相应位置的掺气浓度进行比较(见图6，图7和表3)。

表3 掺气坎下游临底水流的掺气浓度

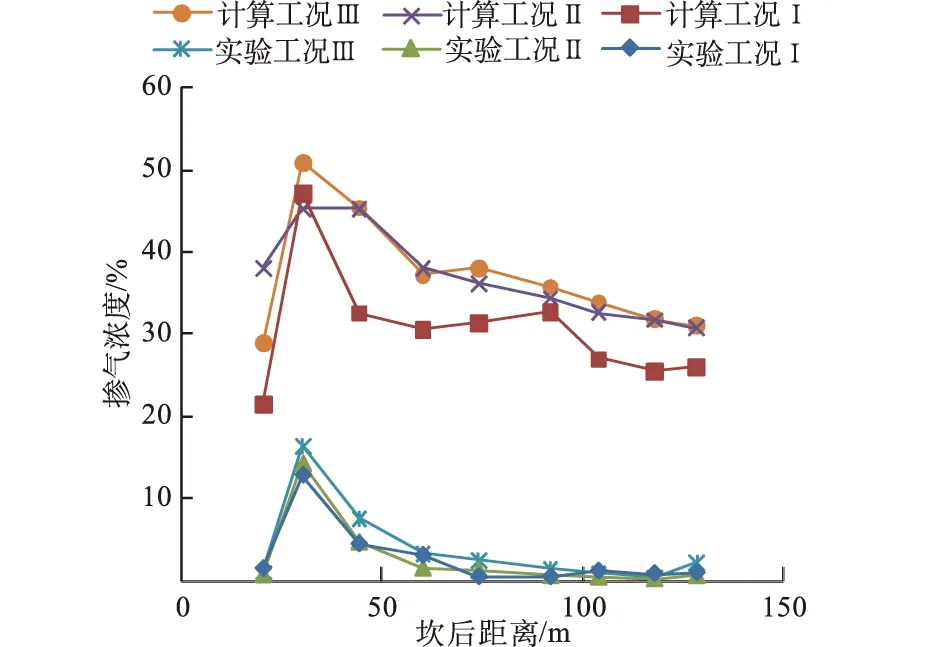
图6 掺气浓度欧拉模型计算值与实验值比较

图7 掺气浓度VOF模型计算值与实验值比较

图中显示欧拉模型和VOF模型计算的坎后掺气浓度与实验值均有较大的偏差。

欧拉模型计算的掺气浓度沿程变化趋势与实验值大致吻合，造成计算掺气浓度偏大的原因可能有：数值模拟中没有采用类似正态分布的气泡直径而是单一气泡直径,导致各气泡的滑移速度相同, 造成气泡过于集中；计算过程中没有考虑升力的影响，因此气泡的竖向滑移速度偏小, 气泡上浮速度过小，致使气泡过于集中在水体底部。

VOF模型计算的掺气浓度沿程变化趋势与实验值部分吻合，且计算浓度也偏大，其原因可能有：VOF模型在捕捉气液界面方面有明显优势，但在描述水气两相间的力学和运动特性时过于简化，对扩散模型进行相间滑移速度本构关系推导时，由于假设局部动量平衡，因而会有一定的局限性。

8 结 语

通过欧拉模型和VOF隐式时间离散模型并结合紊流模型对某泄洪洞掺气坎的数值模拟计算，可以得到以下结论：在对掺气坎上的水力特性的模拟中，欧拉模型与实验值非常接近。欧拉模型和VOF隐式时间离散模型计算的水舌内缘挑距和空腔负压与实验值大致相符。但是计算的空腔长度均偏大。 欧拉模型和VOF隐式时间离散模型都能模拟一定程度的沿程掺气浓度分布，但是都比实验值偏大。欧拉模型模拟的沿程掺气浓度分布与实验值沿程变化趋势比较一致，而VOF隐式时间离散模型只能部分模拟掺气浓度实验值沿程变化趋势。

相比于VOF模型，欧拉模型在模拟水气两相间的相间作用力和运动特性时有很大程度的改善，可以在一定程度上更精确地模拟掺气水流的坎上水力特性和空腔特性。但是依然可以看到这2种模型在模拟空腔长度和掺气浓度沿程变化方面的不足之处，今后要加强对这方面的研究。

参考文献：

[1] 邓 军，许唯临.高水头岸边泄洪洞水力特性的数值模拟[J].水利学报，2005，(10) :1209-1218．(DENG Jun, XU Wei-lin.Numerical Simulation of Hydraulic Characteristics of High Head Spillway Tunnel[J] .Journal of Hydraulic Engineering, 2005,(10):1209-1218.(in Chinese))

[2] 刁明军.高坝大流量泄洪消能数值模拟及实验研究[D].成都: 四川大学,2004 .(DIAO Ming-jun.Numerical Simulation and Experiment Study on Flood Discharge and Energy Dissipation of High Dam With Large Discharge[D].Chengdu：Sichuan University, 2004.(in Chinese))

[3] 张晓东.泄洪洞高速水流三维数值模拟[D] .北京：中国水利水电科学研究院，2004 .(ZHANG Xiao-dong.Three Dimensional Numerical Simulation of High Velocity Flow in Spillway Tunnels[D].Beijing: China Institute of Water Resources and Hydropower Research,2004.(in Chinese))

[4] 覃昕慧，徐玲君，李国栋,等.溢洪道掺气坎二相流数值模拟[J] .水力学与水利信息学进展，2009，(3):590-594.(QIN Xin-hui, XU Ling-jun, LI Guo-dong,etal.Numerical Modelling of Two-phase Flows on Aerator in Spillway[J].Advances of Hydraulics and Water Conservancy Information, 2009, (3): 590-594.(in Chinese))

[5] 张宏伟，刘之平，张 东,等.挑坎下游高速掺气水流的数值模拟[J].水利学报,2008,39(12) :1302-1308.(ZHANG Hong-wei, LIU Zhi-ping, ZHANG Dong,etal.Numerical Simulation of Aerated High Velocity Flow Downstream of an Aerator[J] .Journal of Hydraulic Engineering, 2008, 39(12): 1302-1308.(in Chinese))

[6] 江 帆，黄 鹏.Fluent高级应用与实例分析[M].北京：清华大学出版社，2008.(JIANG Fan, HUANG Peng.Senior Application and Instance Analysis of Fluent[M].Beijing: Tsinghua University Press, 2008.(in Chinese))

[7] 周立行.湍流两相流动与燃烧数值模拟[M].北京: 清华大学出版社, 1991.(ZHOU Li-xing.Numerical Simulation of Two-phase Turbulent Flow and Combustion[M].Beijing: Tsinghua University Press,1991.(in Chinese))

[8] 谭立新.水气二相流数值模拟研究[D].成都: 四川大学, 1999.(TAN Li-xin.Mathematical Modelling of Air-water Two-Phase Flows[D].Chengdu：Sichuan University, 1999.(in Chinese))

[9] 张宏伟 .掺气水流双流体模型数值模拟研究[D] .西安：西安理工大学，2002.(ZHANG Hong-wei.Study on Numerical Simulation of Aerated Water Flow with a Two-fluid Model[D] .Xi’an：Xi’an University of Technology, 2002.(in Chinese))

[10] 付祥钊，龙天渝.计算流体力学[M].重庆:重庆大学出版社，2007.(FU Xiang-zhao, LONG Tian-yu.Computational Fluid Dynamics[M].Chongqing: Chongqing University Press ,2007.(in Chinese))

[11] 江春波，张永良.计算流体力学[M].北京:中国电力出版社，2007.(JIANG Chun-bo, ZHANG Yong-liang.Computational Fluid Dynamics[M].Beijing: China Electric Power Press, 2007.(in Chinese))