DVC中基于广义高斯分布的WZ帧重构算法*

刘杰平 何越盛

(华南理工大学 电子与信息学院，广东 广州 510640)

分布式视频编码(DVC)是建立在Slepian 等［1-2］提出的分布式信源编码理论基础上的一种新型的视频编码框架.与传统的视频编码标准(MPEG-x，H.26x 等)相比，DVC 将利用帧间统计相关性进行的运动估计和运动补偿转移到解码端，具有编码简单、解码较复杂的特点，这一特点使得它特别适合应用于计算能力和内存容量都受限的无线视频终端，如无线视频监控、无线PC 相机、移动视频电话等，为满足新的视频应用提供了很好的解决方案［3-4］.在DVC 系统中，由于WZ(WZ Wyner-Ziv)帧编码后传输到解码端的只是部分效验比特，因此为了提高WZ 帧的重构质量，通常需要利用边信息进行辅助重构，重构算法的好坏直接影响解码重构WZ 帧的图像质量［5-10］.Aaron 等［11］提出一种直接重构算法，利用Slepian-Wolf 解码输出和边信息重构WZ 帧，该算法没有利用原始信息与边信息之间的相关性，算法比较简单.Kubasov 等［12］提出一种最小均方误差重构算法(MMSE)，是均方误差准则下的一种最佳重构算法，利用边信息与原始像素之间的相关模型计算像素的期望值并将其作为重构值，还提出一种多边信息的MMSE 重构方法，多边信息的生成在一定程度上增加了解码端的复杂度.文献［13］中指出视频图像的像素值是离散的，提出一种新的考虑了离散像素值的重构方法.实验结果表明，该方法效果比直接重建好，但稍差于MMSE 重建，并且增加了复杂度.张晓斐等［14］从用于插值边信息的前后帧中提取的特征预测重构帧的下一个比特，并进一步基于该预测比特对重构时的概率密度函数(PDF)进行修改，实现了在传输较少比特平面时获得较高的重构WZ 帧的质量.杨春玲等［15］考虑了视频中帧内和帧间的相关性，结合量化区间中的双向运动补偿，提出一种像素域分布式视频编码双向运动补偿重建算法.文献［12-14］中都是用Laplacian 分布做为相关噪声模型的重构方案.然而，Laplacian 分布并不是最佳的相关噪声模型［16］，文中将广义高斯分布(GGD)用于WZ 帧重构模块，在基本不增加解码复杂度的情况下，有效改善了重构WZ 帧图像的质量，提高了率失真性能.

1 分布式视频编码

典型的像素域Wyner-Ziv 编码的分布式视频编码方案如图1 所示［11］，文中将文献［11］中Slepian-Wolf 编解码器的Turbo 编解码器换为LDPCA(Low-Density Parity-Check Accumulate)编解码器.通常，将输入的视频序列x1，x2，…，xN(N 为序列的长度)划分为WZ 帧x2i(i=1，2，…)和关键帧(K 帧)x2i-1(i=1，2，…)，对K 帧采用传统的JPEG 或H.264/AVC 等帧内编码，对WZ 帧首先进行均匀量化，量化之后进行位平面抽取，然后由Slepian-Wolf 编码器对上述位平面的比特流进行编码，得到的效验比特传输到解码端.解码端通过对已解码的K 帧进行运动估计、内插等得到边信息(SI)，联合传输到解码端的效验比特由LDPCA 解码器解码，之后输入到重构模块，重构出WZ 帧.

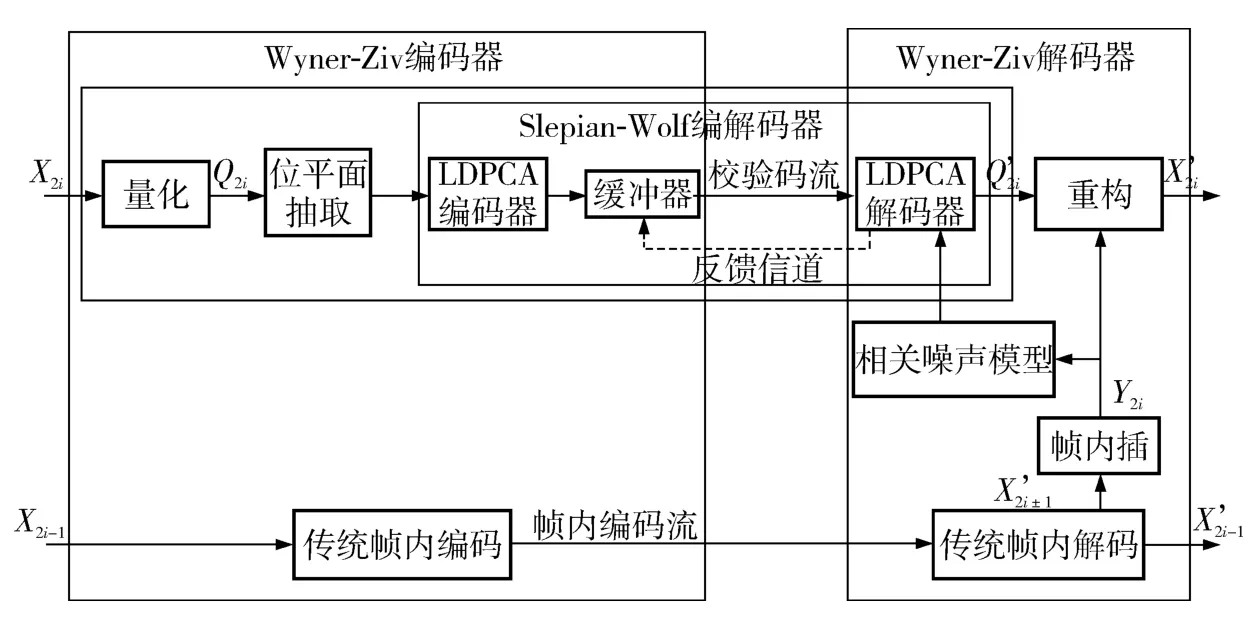
图1 分布式视频编码框架Fig.1 Framework of distributed video coding

2 解码端重构方法

如图1 所示，重构模块的输入是LDPCA 解码器输出的量化值q，因为Wyner-Ziv 编码器传输的仅仅是部分校验比特，解码时需要利用SI 进行联合解码，如果LDPCA 解码失败，解码端向编码端请求更多的效验比特，直到解码成功，从而保证解码恢复的视频质量;相关噪声模型的精确程度一方面直接影响码率，另一方面通过解码输出q'逼近q 的程度间接影响峰值信噪比(PSNR).当相关噪声模型和SI足够精确时，q'=q，这时，如果不改善重构模块，已经无法提高解码WZ 帧的图像质量，重构算法的好坏将直接决定解码WZ 帧的图像质量.

LDPCA 解码输出为q 时，文献［11］的直接重构算法如下:

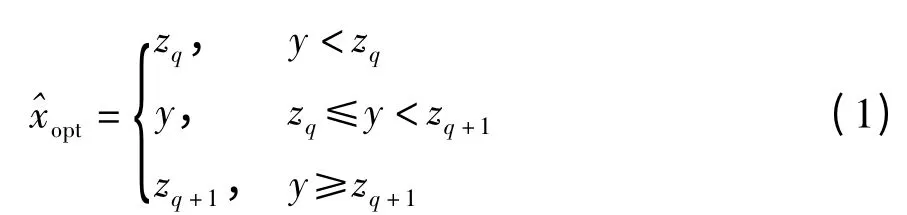
为了进一步提高重构WZ 帧的质量，文献［12］中的MMSE 算法对直接重构算法进行了改进，MMSE 算法考虑了SI 与原始WZ 帧的相关性，认为该相关模型满足式(2)的Laplacian 分布

式中，x 表示原始WZ 帧，p(·)表示概率密度函数，α为Laplacian 参数，，σ2为对前后K 帧的运动补偿的残差帧进行估计得到的方差.

MMSE 重构算法使重构值的均方误差最小，其计算公式为

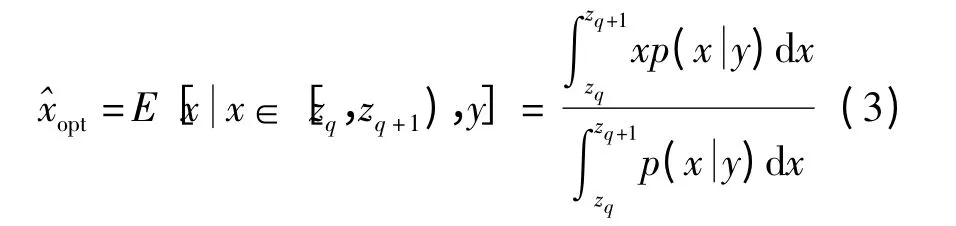
推导出重构算法的闭式表达式为

式中，Δ=zq+1-zq，γ=y-zq，δ=zq+1-y.

MMSE 重构算法的效果取决于Laplacian 分布拟合相关噪声的性能.实际上，Laplacian 分布不是拟合相关噪声的最佳模型［16］，因此该重构结果不是最佳.

3 基于广义高斯分布的WZ 帧重构算法

通常称SI 与原始WZ 帧间的残差为相关噪声，MMSE 重构算法认为该相关噪声模型满足Laplacian分布.然而，Laplacian 分布并不是拟合相关噪声最好的一种分布，文中将GGD 作为相关噪声模型，进行WZ 的重构，获得更好的重构效果.

3.1 广义高斯分布

均值为0 的GGD 为

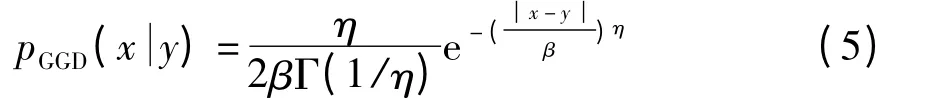
3.2 基于广义高斯分布的WZ 帧重构算法

图2 概率密度函数拟合相关噪声Fig.2 Probability density function fitting correlation noise

基于GGD 的WZ 帧重构的Wyner-Ziv 解码器如图3 所示，图3 中的“相关噪声模型1”采用Laplacian 分布，相关噪声模型参数估计的准确性将直接影响码率.图3 中的重构模块由“相关噪声模型2”和“重建”两部分组成，“相关噪声模型2”采用GGD，重建部分是均方误差最小准则下的重构算法，即采用式(3)实现重建，其中的满足GGD，为了不过多地增加计算的复杂度，将GGD 的形状参数固定为0.5，则式(5)变为

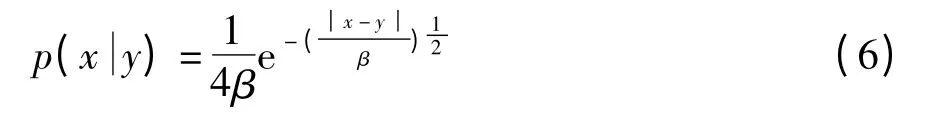
将式(6)代入式(3)，LDPCA 解码输出为q 时，可以推导出基于GGD 的WZ 帧重构算法如下:

图3 Wyner-Ziv 解码器Fig.3 Wyner-Ziv decoder

4 实验结果

为验证文中提出的基于GGD 的WZ 帧重构算法的性能，在图1 所示的Wyner-Ziv 解码器中，分别采用文献［11］的直接重构、文献［12］的MMSE 重构算法与文中提出的WZ 帧重构算法进行对比实验，检验文中提出的重构算法的率失真性能和解码WZ帧图像的质量，实验中GGD 的形状参数固定为0.5，即用式(7)进行WZ 帧重建.实验中，选用QCIF 格式的“Foreman”、“Hall”和“Soccer”视频序列，视频序列长度都是100 帧，其中奇数帧为K 帧、偶数帧为WZ 帧、帧率为30 Hz;实验针对视频序列的亮度分量进行，且只计算WZ 帧的平均码率(rate)和平均峰值信噪比(PSNR);并假设在解码端K 帧可以无失真重建.

图4(a)、(b)、(c)分别是“Foreman”、“Hall”和“Soccer”视频序列不同算法重构WZ 帧的率失真性能的比较结果，对于每个视频序列而言，图4 中的4 个率失真点分别对应WZ 帧编码的最高位平面数M{1，2，3，4}，即对应着重构位平面数从少到多的情况.从图4 可见，在相同码率情况下，与文献［11］直接重构和文献［12］MMSE 重构算法相比，对于不同的视频序列，文中提出的基于GGD 的WZ 帧重构算法均有效提高了率失真性能，且随着码率的增加，文中算法的改善效果更明显.表1 给出了重构位平面数为4 时，不同算法重构WZ 帧的客观质量比较，从表1 可见，对“Foreman”、“Hall”和“Soccer”3 个视频序列，文中算法重构WZ 帧的PSNR 比文献［12］算法分别提高0.32、0.46 和1.01 dB，3 个序列的质量总体平均提高约0.6 dB，3 个视频序列改善效果不同的原因是:“Foreman”、“Hall”和“Soccer”3 个视频序列的运动复杂度不同，它们的运动复杂度依次递增，GGD 对运动复杂度较高的序列相关噪声的拟合更好，“Soccer”序列运动复杂度最高，因此改善的效果最好.

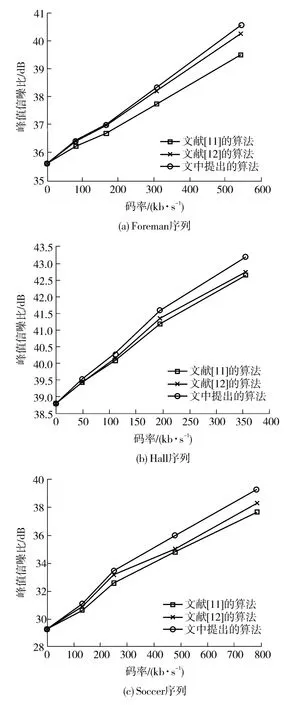
图4 不同重构算法的率失真性能Fig.4 RD(rate-distortion)performance using different reconstruction algorithms

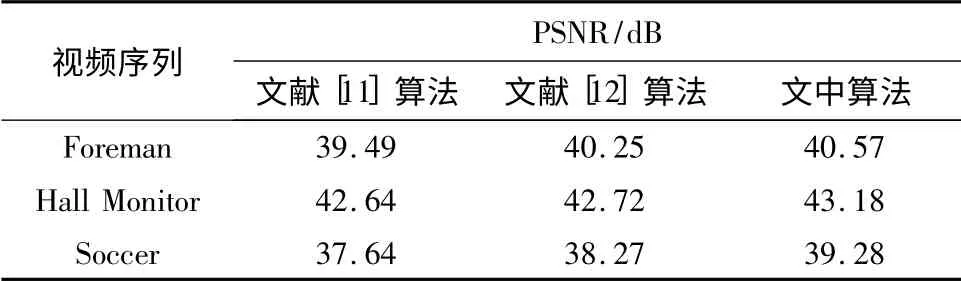
表1 不同算法重构WZ 帧的PSNR1)Table 1 PSNR using different reconstruction algorithms

图5 示出“Foreman”、“Hall”和“Soccer”视频序列各帧的重建质量(解码4 个位平面，M=4)，由图5 可以看出，文中提出的基于GGD 的重构WZ 帧算法均比文献［11］中直接重构和文献［12］中MMSE的算法要好;对比文献［12］中的MMSE 算法，对于解码质量较差的帧，文中算法的重构质量有明显提高，而对于那些解码质量较好的帧，基于GGD 重构算法的重构质量与文献［12］中的MMSE 算法相当;对于不同的视频序列，图5 中显示文中提出的算法均有效提高了重构WZ 帧的图像质量，尤其，对于运动相对剧烈的“Soccer”序列，文中算法重构帧的质量均比文献［12］中的MMSE 算法要好.这是因为GGD 拟合相关噪声的效果比Laplacian 好.总之，GGD 对相关噪声具有更好的拟合性，采用GGD 分布进行WZ 帧重构取得了较好的效果，尤其重构的位平面数越多，相关信息在重构中的作用越明显，文中提出的基于GGD 的重构WZ 帧算法有效提高了重构WZ 帧的图像质量，并改善了率失真性能.

图5 不同算法重构WZ 帧图像客观质量Fig.5 Decoded WZ image quality using different reconstruction algorithms

在计算复杂度方面，从图3 可以看出DVC 解码端的复杂度由LDPCA 迭代译码和重构两部分组成，相对于复杂的LDPCA 迭代译码，重构部分的复杂度是微不足道的，文中算法在对量化值进行重构时引入了GGD 作为相关噪声模型，即图3 中的“相关噪声模型2”，因此对重构部分增加了一定的计算量，表2 中给出了不同序列在采用文献［12］中的MMSE重构算法和采用文中基于GGD 重构算法的情况下平均每帧的重构时间，从实验结果可以看出，文中算法每帧的平均重构时间有所增加，这是因为GGD 参数估计比Laplacian 参数估计复杂.需要指出的是，文中算法增加的计算复杂度仅仅是解码端的复杂度，对编码端没有影响，DVC 中更加关注的是编码端的复杂度.目前，DVC 的瓶颈是解码性能，文中提出的算法恰恰是提高了解码性能，且对运动相对剧烈的视频序列解码性能提高的效果更明显，因此对于文中算法在改进性能的同时，平均每帧重构时间增加1.6～3.5 ms，这对于DVC 来说是可以接受的.

表2 采用不同重构算法的重构时间Table 2 Reconstructing time using different reconstruction algorithms

5 结论

基于DVC 系统WZ 帧重构的特点，文中对已有WZ 帧重构算法的性能进行了分析比较，研究了Laplacian 分布和GGD 对相关噪声的拟合，对形状参数固定为0.5 的GGD 相关噪声拟合实验表明，GGD比Laplacian 能更好地拟合相关噪声.文中充分考虑了边信息与原始WZ 帧之间的相关性，用GGD 作为该相关模型，计算边信息已知情况下WZ 的条件期望作为WZ 重构值;提出了基于GGD 的WZ 帧重构算法，推导出形状参数为0.5 的GGD 为相关模型的重构WZ 帧的闭式表达式.实验结果显示，文中的重构算法与直接重构和MMSE 重构算法相比，能更有效地提高重构WZ 帧的图像质量，并且能有效改善率失真性能.

［1］Slepian D J，Wolf K J.Noiseless coding of correlated information sources［J］.IEEE Transactions on Information Theory，1973，19(4):471-480.

［2］Wyner A D，Ziv J.The rate-distortion function for source coding with side information at the decoder ［J］.IEEE Transactions on Information Theory，1976，22(1):1-10.

［3］Girod B，Aaron A，Rane S.Distributed video coding［J］.Proceedings of the IEEE，2005，93(1):71-83.

［4］Puri R，Majumdar A，Ishwar P.Distributed video coding in wireless sensor networks ［J］.IEEE Signal Processing Magazine，2006，23(4):94-106.

［5］Weerakkody W，Fernando W A C，Kondoz A M.An enhanced reconstruction algorithm for unidirectional distributed video coding［C］∥Proceedings of the 12th IEEE International Symposium on Consumer Electronics (ISCE’08).Algarve:Portugal，2008:1-4.

［6］Roca A，PradesNebot J，Delp E J.Adaptive reconstruction for Wyner-Ziv video coders［C］∥Proceedings of Visual Communications and Image Processing.San Jose，CA，SPIE，2009:1-9.

［7］Ralph Hänsel，Erika Müller.Improved reconstruction for distributed video coding［C］∥Ultra Modern Telecommunications ＆ Workshops.Russia:St Petersburg，2009:1-5.

［8］Shim S Y，Han J K，Bac J.Adaptive reconstruction scheme using neighbour pixels in PDWZ coding［J］.Electronics Letters，2010，46(9):626-628.

［9］Zhang Y S，Xiong H K，He Z H，et al.Reconstruction for distributed video coding:a context-adaptive markov random field approach［J］.IEEE Transactions on Circuits and Systems for Video Technology，2011，21(8):1100-1114.

［10］Micallef J J，Farrugia R A，Debono C J.Selective reconstruction of low motion regions in distributed video coding［C］∥EuroCon.Zagreb:IEEE，2013:87-92.

［11］Aaron A，Zhang R，Girod B.Wyner-Ziv coding of motion video［C］∥Proceedings of the 36th Asilomar Conference on Signals，Systems and Computers.Pacific Grove，USA:IEEE，2002:240-244.

［12］Kubasov D，Nayak J，Guillemot C.Optimal reconstruction in Wyner-Ziv video coding with multiple side information［C］∥Proceedings of the 9th International Workshop on Multimedia Signal Processing 2007.Grete，IEEE，2007:183-186.

［13］Du B，Shen H.A novel reconstruction approach for pixeldomain distributed video coding［C］∥International Conference on Future Computer and Communication (ICFCC’2010).Wuhan:IEEE，2010:614-618.

［14］张晓斐，熊红凯，张永生.基于比特平面预测的分布式视频WZ 帧重构方法［J］.中国图象图形学报，2009，14(10):2172-2176.Zhang Xiao-fei，Xiong Hong-kai，Zhang Yong-sheng.Bit plane prediction based WZ frame reconstruction in DVC［J］.Journal of Image and Graphics，2009，14(10):2172-2176.

［15］杨春玲，苏桌涵.像素域分布式视频编码双向运动补偿重建算法［J］.华南理工大学学报:自然科学版，2011，39(12):7-12.Yang Chun-ling，Su Zhuo-han.Bi-directional motioncompensated algorithm for pixel-domain video coding［J］.Journal of South China University of Technology:Natural Science Edition，2011，39(12):7-12.

［16］Maugey T，Gauthier J.Pesquet-Popescu B.Using an exponential power model for Wyner-Ziv video coding［C］∥Proc IEEE ICASSP.Dallax Texas:IEEE，2010:2338-2341.