基于单演特征和稀疏表示的人脸识别*

章权兵 黄翔 徐争元 苏娟

(安徽大学 计算智能与信号处理教育部重点实验室，安徽 合肥 230039)

虽然人脸识别在最近几十年已经被广泛研究，但由于受遮挡、姿态变化和光照［1］等影响，其识别性能依然受到很大的限制.因此在真实情况下提高人脸识别的鲁棒性仍有必要.由此很多经典的人脸特征提取和分类方法被提出，包括子空间学习的Eigenface［2］、Fisherface［3］、Laplacianface［4］、基于Gabor 特征的分类［5］以及具有机器学习功能的支持向量机(SVM)［6］等.

2008年，Wright 等［7］首次将稀疏表示引入到人脸识别中，提出了基于稀疏表示的分类(SRC)方法.该方法是将训练样本作为字典，通过l1模最小化技术得到待识别图像在字典上的稀疏表示系数，并求解最小残差来进行识别.它在鲁棒的人脸识别中指出了新的方向，但仍然存在一些问题，如要求图像对齐、人脸特征为整体特征等.这些都大大降低了识别的鲁棒性.因此后来有一些改进的算法被提出［8-10］，如Yang 等［11］将Gabor 特征引入到SRC 中，提出了基于Gabor 特征的稀疏表示分类(GSRC)方法，由于Gabor 特征是从局部区域抽取，对影响图像的一些因子不是特别的敏感，用它做字典将能够提高人脸的识别率.

尽管GSRC 获得了不错的效果，但Gabor 仅仅提取了图像的幅度信息，对于相位信息并没有考虑.另外Gabor 变换本身需要在不同尺度和不同方向上进行，这提高了计算时间和存储空间［12-13］.针对这些问题，文中基于单演信号理论［14-16］的思想，将它与稀疏表示进行联合，获得了不错的识别效果.

1 人脸图像的稀疏表示

已知有n 幅人脸图像，分为k 类，每一类有ni幅.对这些图像进行处理(下采样或特征提取等)，从而获得训练样本.设第i 类样本训练集合为Ai=［vi，1，vi，2，…，vi，ni］Rm×ni，若此时有一个同类的样本yRm，则它可以由此类中的所有训练样本线性表示，即

但在实际中，往往测试样本属于哪一类是未知的，这就需要在整个训练样本类中去寻找.定义一个拥有k 类，包含所有训练样本的字典A，A=［A1A2… Ak］Rm×n，此时测试样本便可以由所有训练样本线性表示

这里的α 是一个稀疏系数向量.理论上，求得的α只在与测试样本相关的训练类别上对应的系数不为0，而在不相关类上对应系数为0.因此可以通过观察α 中非0 的部分来指定测试样本属于哪一类.

对于α 的求解可以转换为求解l0范数的问题，即

由于降维的影响，A 的列数往往会大于行数，即n＞m，此时求解l0问题将会是一个NP-hard 问题，很难在实际中精确地解出.

近年发展的压缩感知理论证明:如果系数足够稀疏，那么l0范数问题可以转换为求解l1范数最小化问题［17］

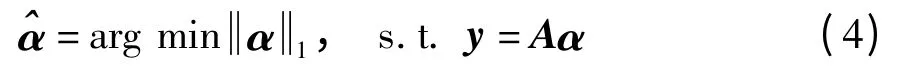
这是理想情况下求解α 的方法.然而，由于受噪声和误差的影响，由Aα 重构的与原始的y 会有一定的偏差，所以问题(4)可转化为下面的最小化问题

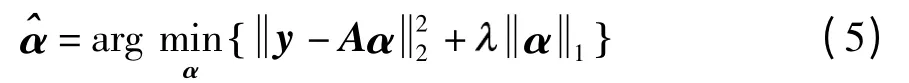
前一项是基于整个字典的重构残差，后一项是正则项，其作用是使系数α 尽量稀疏.通过估计求得稀疏表示，再求取基于部分字典的残差，这里的部分字典指的是对应一个类的所有样本，如对应第i 类公式为

最后可根据残差ri最小原则来确定测试样本所属类别，即识别出所给定人脸图片的身份.

2 基于单演特征的稀疏表示

2.1 Log-Gabor 滤波

Gabor 变换首次由Dennis Gabor 提出，由于它的特性类似于视觉神经细胞工作机理，所以被经常用于图像的特征提取.虽然能够提取多尺度性和多方向性的图像局部信息，但它并非严格意义上的带通滤波器.当带宽大于一倍频率时，Gabor 变换的实部会产生直流分量［18］，而直流分量会影响构造相互正交的滤波器对.为了弥补Gabor 小波在使用中的限制，Filed［19］提出了Log-Gabor 滤波器，其优点在于不仅能够去除直流分量的干扰，不用考虑带宽限制问题，而且在相同振幅下，其在高频的拖尾要长些，以致覆盖的频率范围更大，减少了计算量.Log-Gabor的频率响应公式如下所示:

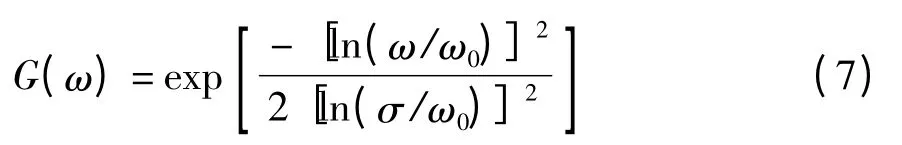
这里σ=σratioω0是带宽比例因子，ω0=(minμs－1)－1是中心频率，min为最小波长，μ 为波长的乘法因子，s 为尺度因子，σratio为比值σ/ω0.

2.2 单演特征

单演信号是通过Riesz 变换得到的一维解析信号的二维泛化.它可估计信号的局部振幅、局部方向和局部相位.Riesz 变换如下

式中，f(z)是输入信号，z=(x，y)，滤波器hx和hy分别对应的二维频域响应为，这里ω=(ωx，ωy)，fx(z)表示在x 方向上的Riesz 变换，fy(z)表示在y 方向上的Riesz 变换.易得Riesz 核的空间表示为

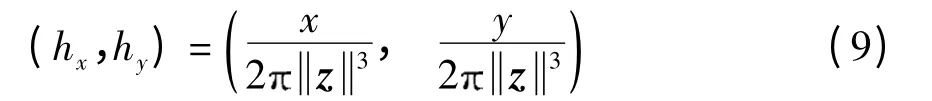
单演信号fM(z)为

在实际应用中，信号的长度是有限的，需要先对图像进行带通滤波处理.由于Log-Gabor 滤波器是带通滤波器，为了尽量描述图像的特征信息，通过调节滤波器的尺度因子s 来获取多个尺度单演特征(s越大，越能体现整体轮廓信息，s 越小，越能体现细节信息).优化后的单演信号flog-M为

其中，flog(z)=f(z)* F－1(G(ω))，F－1表示二维傅里叶逆变换.flog(z)表示的是信号经过了Log-Gabor 滤波，flog-x(z)表示滤波后的信号在x 方向上的Riesz变换，flog-y(z)表示滤波后的信号在y 方向上的Riesz变换.由此图像的局部幅度、局部相位和局部方向分别为

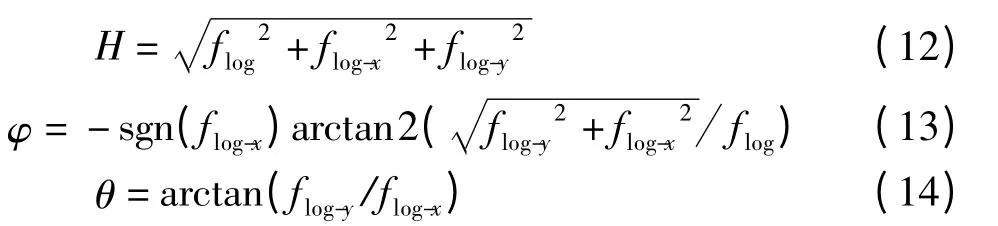
这里，H 描述了图像的局部能量信息，φ 描述了图像的局部结构信息，θ 描述了图像的局部几何信息.尺度因子s 分别取1、2、3 时，单演信号的特征图如图1所示.

图1 单演特征图Fig.1 Images of monogenic features

2.3 MSRC 方法

不同于Gabor 运算，单演特征能够较好地表达出图像的能量特征、结构特征和几何特征.而结构特征包含了大部分的图像信息，相对能量特征不容易受光照影响.将其作为字典用于识别时，会得到较好的效果.

MSRC 的算法具体流程如下.

(1)已知训练样本集A 和测试样本y.

(2)选取不同的尺度因子，在x 和y 方向分别进行Log-Gabor 滤波，然后通过Resize 变换，获得单演特征图.将不同尺度因子s 对应的特征图以列的形式连接在一起构造一个局部特征描述子，最终获得训练样本特征集M(A)和测试样本特征M(y).

(3)利用主成分分析(PCA)和线性判别分析(LDA)相结合的方式将M(A)和M(y)进行降维处理，得到低维训练样本特征集X(A)和测试样本特征集X(y).

(4)归一化X(A)和X(y).

(5)通过l1模最小化方法求解稀疏系数，即

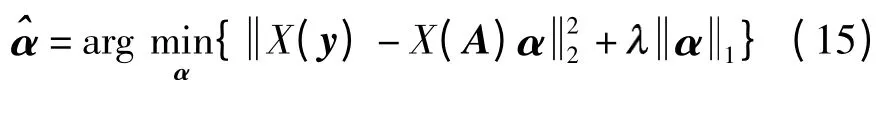
(6)取对应类的稀疏系数来计算各类合成的样本与原始样本的残差，即

式中，δi()是一个从整体系数中选取与第i 类相关的系数，即

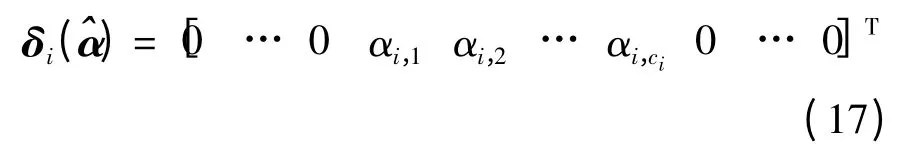
(7)对应最小残差的那个类就是测试样本所属的类，即identify(y)=arg min{ri(y)}.

从上面很容易发现对图像使用多尺度二维Gabor滤波和多尺度单演滤波都会产生一定的冗余信息.对于Gabor，冗余既来自多尺度，又来自多方向.但对于多尺度单演特征，由于其幅度、相位、方向都是正交的，冗余仅仅来自对尺度的表示.因此使用后者更有意义.

3 实验结果

利用实验验证算法的有效性，首先在AR 库上分别比较了不同尺度单演特征的人脸识别结果以及多尺度单演性质(能量、结构和几何特征)图的人脸识别结果.然后通过对Extend Yale B 和AR 人脸数据库的实验来比较MSRC 与SRC、GSRC 算法的识别性能.多尺度单演信号的参数设定为:min=4，μ=0.64，σratio=1.7，尺度数为3.实验所用平台是Intel(R)Core(TM)2 处理器，主频2.80GHz，2.00GB 内存，MATLAB7.9 版本，Windows 7 系统.

3.1 不同单演特征图的识别效果

实验中所使用的图像单演特征是一个联立特征，它包含了不同尺度、不同性质的单演特征.在AR 库上对这些特征图分别进行了实验比较，主成分分析(PCA)的维数分别取100、200、300，线性判别分析(LDA)的维数与训练的样本类数一致，实验结果如表1 和表2 所示.

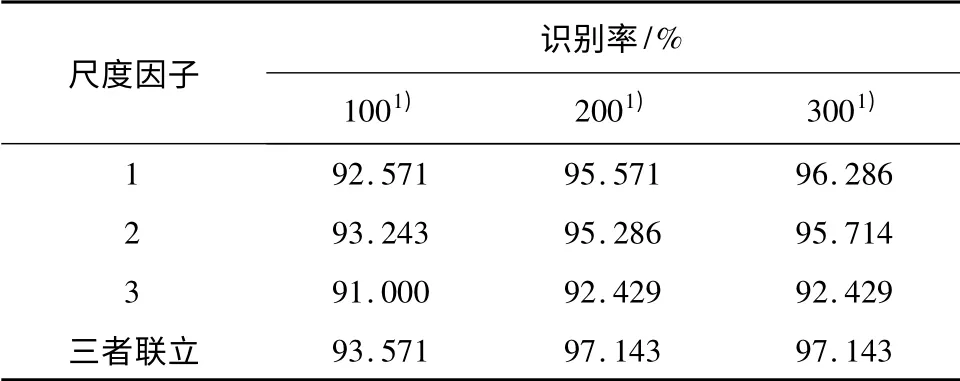
表1 不同尺度单演特征的识别率Table 1 Rate of recognition based on different scales of the monogenic feature

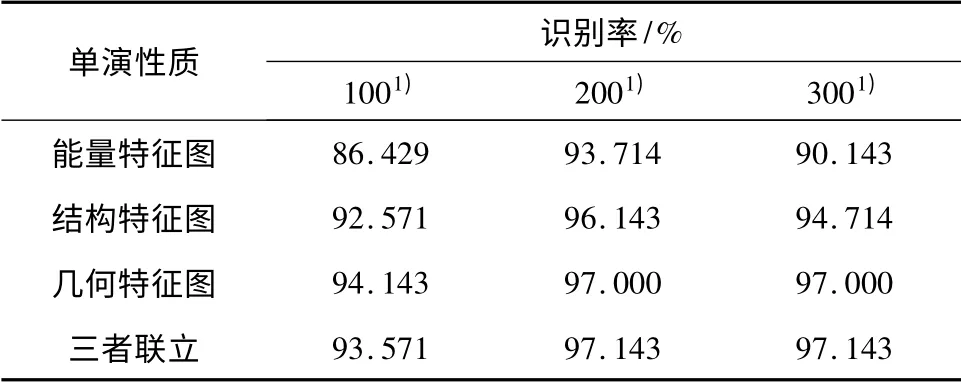
表2 不同单演性质图的识别率Table 2 Rate of recognition based on different monogenic nature

表1 是尺度因子s 取不同值时的人脸识别率.从表1 中可看出，s=1 和s=2 时，识别率接近，s=3时，识别率有明显的下降趋势，但取三者的联立特征得到的识别率最佳.

表2 是不同单演性质(能量、结构和几何特征)的识别结果.从表2 中可看出结构特征图和几何特征图的识别率明显高于能量特征图，这也验证了前面所说的相位信息的重要性.

3.2 Extend Yale B 人脸库上的实验结果

Extend Yale B 人脸库包含10 个人，每个人有64 幅各种不同光照条件下的正面人脸图像.首先将图像尺寸归一化到70 ×80，并从中选取50%图像作为训练样本，剩余作为测试图像.利用上节方法提取特征后，利用PCA 与LDA 相结合的方式进行降维，这里PCA 的维数分别取40、60、80、100、120、140、160、180、200，LDA 的维数与训练的样本类数一致.

图2 显示了SRC、GSRC 和MSRC 在不同PCA维数下的识别率，十字形标记线条表示的是MSRC的识别性能与量化参数的关系曲线.由图可知，文中提出的MSRC 最高识别率为100%，高于SRC 的97.500%和GSRC 的98.438%.Extend Yale B 人脸库由于只受光照变化，而相位基本不受光照影响，所以文中算法能够获得非常好的效果.从图中可见并不是PCA 维数越高，识别效果越好，这表明利用PCA 与LDA 联合降维时，并不是所有的特征向量都是有效的投影方向，过多特征向量往往会影响最终的识别效果.

图2 在Extend Yale B 上的识别率Fig.2 Recognition rate on the Extend Yale B

图3 显示了不同算法在Extend Yale B 上的运行时间，白色直方图表示的是MSRC 算法在库中所有测试图像的识别时间，其长度明显矮于GSRC 算法的直方图，说明此算法能以较短的时间来完成身份的识别.

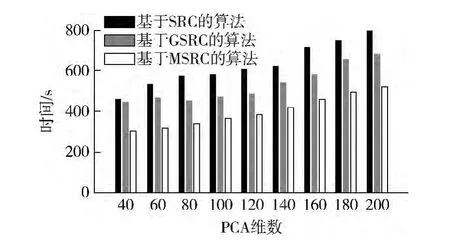
图3 在Extend Yale B 上的时间表现Fig.3 Time performance on the Extend Yale B

3.3 AR 人脸库上的实验结果

AR 人脸库包含有100 人，每个人有14 幅人脸图像，不仅具有光照变化，还有表情的变化.将图像尺寸从165 ×120 归一化到80×59，并从中选取50%作训练样本，剩余作为测试样本.这里仍采用PCA 与LDA 联合方式进行降维.值得注意的是，由于LDA 的默认维数与训练样本类数一致，因此PCA降维的维数应不小于100.PCA 的维数分别取100、120、140、160、180、200、220、240、300.

图4 显示了SRC、GSRC 和MSRC 在AR 库上的识别率，文中提出的MSRC 虽然最高识别率与GSRC 一致，都为97.143%，但是整体平均识别率高于GSRC.

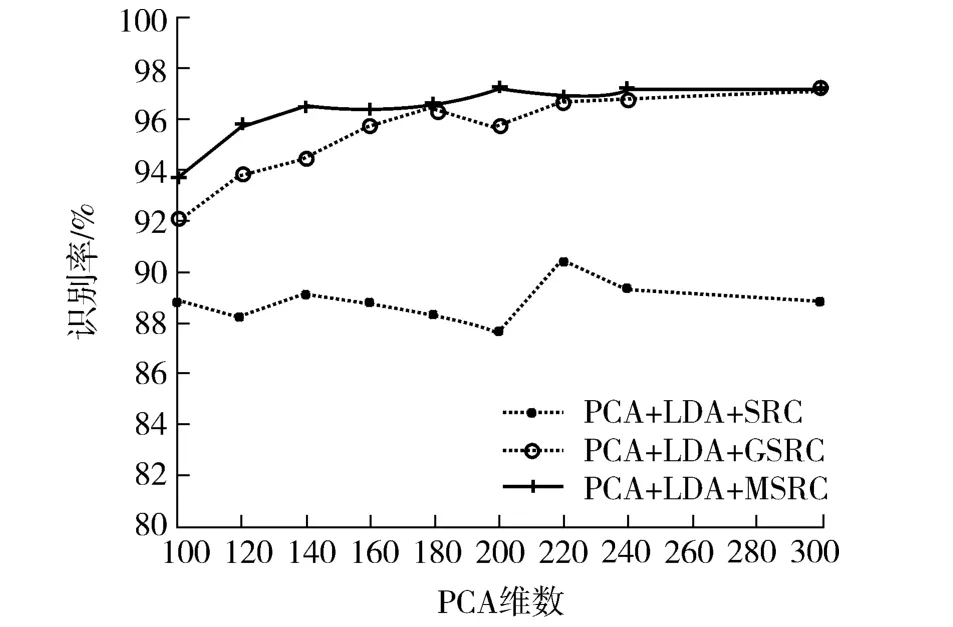
图4 在AR 库上的识别率Fig.4 Recognition rate on the AR

图5 显示了不同算法在AR 库上的运行时间，从图中可看出文中所提算法虽然时间也很长，但是相对其它两种算法依然是最优的.

图5 在AR 库上的时间表现Fig.5 Time performance on the AR

4 结论

现实中所获得的训练样本数量往往受限，这就需要在稀疏表示中获得一个较鲁棒的字典.基于此，文中将单演信号理论引入到稀疏表示的人脸识别中，通过提取图像的局部能量、局部结构、局部几何信息作为特征字典应用于稀疏表示分类中.在Extend Yale B 和AR 上分别进行仿真实验，提出的MSRC 在速度和识别率上都高于GSRC，从而验证了文中算法的有效性.

［1］Tan Xiao-yang，Triggs Bill.Enhanced local texture feature sets for recognition under difficult lighting conditions［J］.Image Processing，2010，19(6):1635-1650.

［2］Turk M，Pentland A.Eigenfaces for recognition［J］.Journal of Cognitive Neuroscience，1991，13(1):71-86.

［3］Belhumeur P，Hespanha J，Kriegman D.Egienfaces vs fisherfaces:recognition using class specific linear projection［J］.IEEE Transaction on Pattern Analysis Machine Intelligence，1997，19(7):711-720.

［4］He X，Yan S，Hu Y，et al.Face recognition using laplacianfaces［J］.IEEE Transaction on Pattern Analysis Machine Intelligence，2005，27(3):328-340.

［5］Liu C，Wechsler H.Gabor feature based classification using the enhanced fisher linear discriminant model for face recognition［J］.IEEE Transaction on Image Processing，2002，11(4):467-476.

［6］HeiseleB，HoP.Face recognition with support vector machine:global versus component-based approach ［C］∥Proceedings of the Eighth International Conference on Computer Vision.Vancouver，BC:ICCV，2001:688-694.

［7］Wright J，Yang A Y，Ganesh A，et al.Robust face recognition via sparse representation［J］.IEEE TPAMI，2008，31(2):210-227.

［8］Zhang L，Yang M，Feng X.Sparse representation or collaborative representation:which helps face recognition?［C］∥Proceedings of IEEE Conference on Computer Vision.Barcelona:IEEE，2011:471-478.

［9］Yang M，Zhang L，Yang J，et al.Robust sparse coding for face recognition［C］∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Hong Kong:IEEE，2011:625-632.

［10］Wagner A，Wright J，Ganesh A，et al.Robust alignment and illumination by sparse representation ［J］.IEEE Transactions on Pattern Recognition Analysis and Machine Intelligence，2012，34(2):372-386.

［11］Yang M，Zhang L.Gabor feature based sparse representation for face recognition with Gabor occlusion dictionary［C］∥Proceedings of European Conference on Computer Vision.Berlin:IEEE，2010:448-461.

［12］Zhang W，Shan S，Gao W，et al.Local gabor binary pattern histogram sequence(LGBPHS):a novel nonstatistical model for face representation and recog-nition ［C］∥Proceedings of IEEE International Conference on Computer Vision.Hong Kong:IEEE，2005:786-791.

［13］Zhang B，Shan S，Chen X，et al.Histogram of gabor phase patterns(HGPP):a hovel object representation approach for face recognition ［J］.IEEE Transaction on Image Processing，2006，16(1):57-68.

［14］Felsberg M，Sommer G.The monogenic signal［J］.IEEE Transaction on Signal Processing，2001，49(12):3136-3144.

［15］Yang M，Zhang L，Zhang L，et al.Monogenic binary pattern (MBP):a novel feature extraction and representation model for face recognition［C］∥Proceedings of the 20th International Conference on Pattern Recognition.Piscataway，NJ:IEEE，2010:2680-2683.

［16］Yang M，Zhang L，Shiu S，et al.Monogenic binary coding:an efficient local feature extraction approach to face recognition［J］.IEEE Transaction on Information Forensics and Security，2012，7(6):1738-1751.

［17］Donoho David L.For most large underdetermined systems of linear equations，the minimal Linorm solution is also the sparsest solution［J］.Communication on Pure and Applied Math，2006，59(6):797-829.

［18］Fischer S V，Sroubek F，Perrinet L，et al.Self-Invertible 2D Log-Gabor wavelet［J］.International Journal of Computer Vision ，2007，75(2):231-246.

［19］Field D J.Relations between the statistics of natural images and the response properties of cortical cells ［J］.Journal of the Optical Society of American，1987，4(12):2379-2394.