考虑板筋参与作用的RC框架有效翼缘宽度简化公式*

王素裹

(福州大学 土木工程学院，福建 福州 350116)

在地震震害中，钢筋混凝土(RC)框架会出现落层倒塌［1］和“强梁弱柱”的破坏形态，“强梁弱柱”的破坏形态在我国的汶川地震［2］和芦山地震［3］以及2011年的土耳其地震［4］中均普遍存在，通过研究分析［5-8］，可知主要原因之一是未合理考虑现浇楼板内的板筋参与梁端抗弯，使梁端的实际抗弯能力大幅增加，造成框架梁端先于柱端出现塑性铰.对于板筋对梁端抗弯的参与作用，较为方便的考虑方法是通过有效翼缘宽度bf进行估算，各国规范对bf取值的相关规定各不相同.新西兰规范［9］取梁中到两侧各1/4 梁跨度、梁中到两侧各1/2 梁肋间距、有正交边梁时从梁中到两侧各1/4 边梁跨、无正交边梁时梁中到两侧各1 倍边柱宽的小值.美国ACI规范［10］对中间榀框架取1/4 梁跨、8 倍板厚和1/2梁肋净距的小值，对边榀框架取梁侧边向外1/12 梁跨度、6 倍板厚和1/2 梁肋间净距的小值.欧洲EC8规范［11］按以下情况取值:对与边柱相连的框架梁，无正交边梁时取为柱宽，有正交边梁时则取柱宽+每侧4 倍板厚;对与中柱相连的框架梁，无正交梁时取柱宽+每侧2 倍板厚，有正交梁时则取柱宽+每侧4 倍板厚.我国现行抗震规范［12］对bf的取值没有明确规定，只在条文说明中指出:当计算梁端抗震承载力时，若计入楼板内的钢筋，可提高框架结构“强柱弱梁”的程度，但规范中并未对其进行量化.鉴于目前bf取值尚不统一的情况，学者们对其进行了探讨［7，13-18］，如文献［13］中提出取框架梁每侧6 倍板厚，文献［14］中提出取每侧1 倍梁宽，文献［15］中提出对应1/50 层间位移角时每侧取1.6倍横向梁宽.

研究表明［7，15-18］，节点类型和轴压比为影响bf取值的两个重要因素，文中针对这两个因素设计多个RC 空间框架，进行侧向荷载作用下的仿真模拟，结合板筋应力分布情况和数值回归分析得出方便用于实际结构设计的bf简化公式，给出能更好地实现“大震不倒”设防目标的改进设计建议，并进行了工程实例验证.

1 有效翼缘宽度的定义

试验及数值模拟均表明［19-21］，参与梁端抗弯的板筋的实际应力沿正交梁方向不均匀分布，从框架梁由近到远逐渐减小，如图1 所示.用有效翼缘宽度bf估算板筋参与梁端抗弯的效果时，对板筋实际应力分布进行如下折算和简化:假定bf范围内的板筋全部参与框架梁抗弯并能达到屈服强度，应力在该范围内均匀分布，如图2 所示.bf是针对框架梁负弯矩作用端且基于抗弯强度得到的，其取值依据是参与框架梁抗弯的板筋，与现行混凝土结构设计规范［22］中的翼缘计算宽度b'f不同，b'f为框架梁正弯矩作用处因楼板处于受压区而考虑将楼板作为翼缘时对梁刚度增大的影响.根据已有研究［15，17-19］，bf取值与结构侧移有关，而非固定值.由上述bf定义建立板筋实际应力分布与bf内应力分布的关系如下:负弯矩下，参与作用的板面和板底钢筋产生的拉力之和与bf范围内的板筋拉力之和相等.则bf可按下式计算:

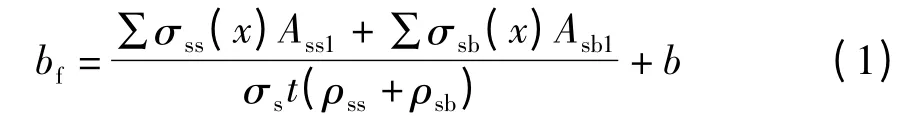
式中，σss(x)和σsb(x)分别为侧移下板面和板底钢筋沿正交梁跨的实际应力分布，Ass1和Asb1分别为板面和板底每根钢筋的面积，σs为梁端矩形截面内的受拉钢筋应力，b 为框架梁宽，t 为楼板厚度，ρss和ρsb分别为板面和板底钢筋配筋率.

图1 板筋应力的实际分布Fig.1 Real stress distribution of slab reinforcement

图2 有效翼缘宽度范围内的板筋应力分布Fig.2 Stress distribution of slab reinforcement within effective flange width

用式(1)计算bf时，需先求得板筋沿正交梁方向的实际应力，而不同位置的板筋应力不同，因而增大了实际结构设计时的计算量和操作难度.为便于结构设计，文中设计了RC 空间框架模型来对bf的取值进行数值回归分析，得出对应1/50 层间位移角时bf的近似计算简化公式.

2 RC 空间框架模拟

2.1 RC 空间框架基本信息

6 个RC 空间框架结构模型的平面布置如图3所示.侧向荷载按倒三角形荷载施加，F1∶F2=1∶2，施加方向如图4 所示.框架梁截面尺寸为200 mm ×400 mm;板厚100 mm.楼面均布恒载3.5 kN/m2、均布活载2.0 kN/m2，墙载为3.6 kN/m.二层柱顶施加轴压力来模拟上层传递的竖向荷载，各模型采用不同柱截面尺寸使底层中柱轴压比n 分别为0.9、0.8、0.6、0.5、0.4、0.3(0.9～0.3 为实际工程中常见的轴压比分布范围)，各模型柱截面尺寸及轴压比见表1.

图3 结构模型平面布置图(单位:mm)Fig.3 Layout of structure models (Unit:mm)

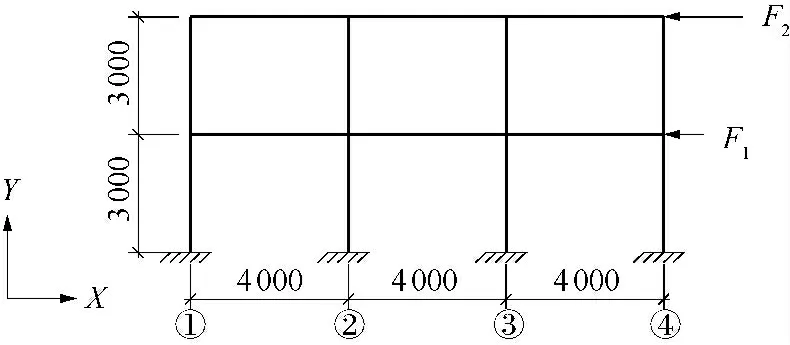
图4 侧向荷载施加示意图(单位:mm)Fig.4 Schematic diagram of lateral load (Unit:mm)

按福州地区三级抗震框架配筋，C40 混凝土，梁、柱、板受力筋采用HRB335 钢筋、箍筋采用HPB300 钢筋.构件配筋均符合实际设计要求.梁内上部钢筋和下部钢筋均为2φ14(φ 仅代表直径，下同);柱截面配筋如图5 所示;梁柱箍筋均为φ8@100/200;板配筋为:面筋φ8@200、底筋φ8@150.

表1 柱截面尺寸及轴压比Table 1 Sectional dimensions and axial compression ratios of columns

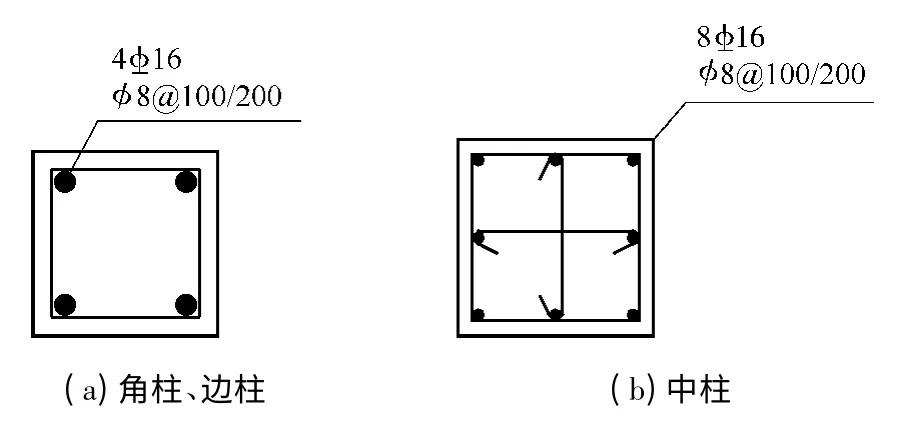
图5 柱截面配筋(单位:mm)Fig.5 Reinforcement details of column sections (Unit:mm)

2.2 模拟方法

根据对称条件取图3 虚线范围进行模拟，在ABAQUS 中建立的模型如图6 所示，对梁、柱、板厚等处进行局部网格细分以提高分析精度，采用已通过试验验证的模拟方法［21］(限于篇幅，试验验证部分在此不再重复)进行模拟:钢筋的应力－应变关系根据现行规范采用双直线模型描述，采用三维杆单元T3D2 模拟，通过* EMBEDDED ELEMENT 实现钢筋与混凝土的连接;混凝土采用三维实体线性缩减积分单元C3D8R 模拟，本构关系按现行混凝土规范并通过塑性损伤模型表达，通过定义取值为0～1的受拉、受压损伤因子dt、dc来描述混凝土内部微裂缝产生后发生的损伤，此时材料力学性能发生软化，通过应变等价原理考虑损伤后的、作为决定屈服面和破坏面依据的有效拉应力和有效压应力，分别见式(2)、(3):

式中，σt、σc分别为进入到软化段后的名义拉应力和压应力，εt、εc分别为进入到软化段后的名义拉应变和压应变，E0为混凝土初始弹性模量，和分别为拉伸和压缩等效塑性应变.

混凝土为抗拉能力较差的脆性材料，因而应正确处理混凝土开裂后的力学行为.结构裂纹区的后继破坏行为通过* TENSION STIFFENING 来体现，实现混凝土开裂后力在钢筋上的传递.该行为可通过后继破坏的应力－应变关系或断裂能破坏准则进行定义，文中模型采用前者进行定义，考虑拉伸硬化后的应力－应变关系如图7 所示，则混凝土开裂后按下式将开裂应变转换为塑性应变

图6 模型的网格划分Fig.6 Mesh generation of the models

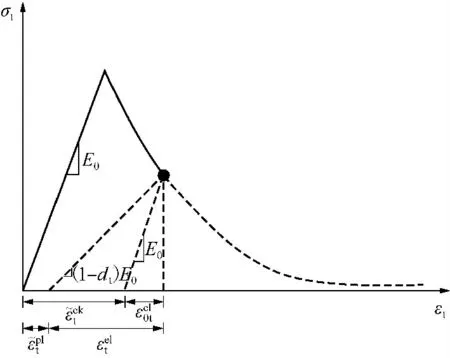
图7 考虑拉伸硬化后的应力–应变关系Fig.7 Stress-strain relationship considering tension stiffening

3 板筋应力分布

首层层间侧移达1/50 层间位移角限值时，各模型第一跨板面和板底钢筋的应力分布如图8 和9 所示.由图8 和9 可知:此时靠近梁端处均有一定数量的板筋达到屈服强度;面筋在框架梁抗弯能力上起的作用大于底筋;通过对边榀(A 榀)框架和中间榀(B 榀)框架的比较可知，A 榀框架在离框架梁端同样距离的板筋应力较B 榀框架的大，这是因为在侧向荷载作用下，A、B 榀平面框架在相同梁跨处产生的负弯矩大致相同，而A 榀框架处仅一侧与楼板相连，能够参与抗弯的板筋比B 榀框架少，因此，需要增大能起作用的板筋应力来承受相同数值的负弯矩.板面和板底钢筋应力均随轴压比降低而增大，当轴压比降为0.3 时，板面钢筋应力在整个正交梁跨范围内全部进入屈服阶段，可见面筋在恰当条件下可全部参与梁端抗弯.

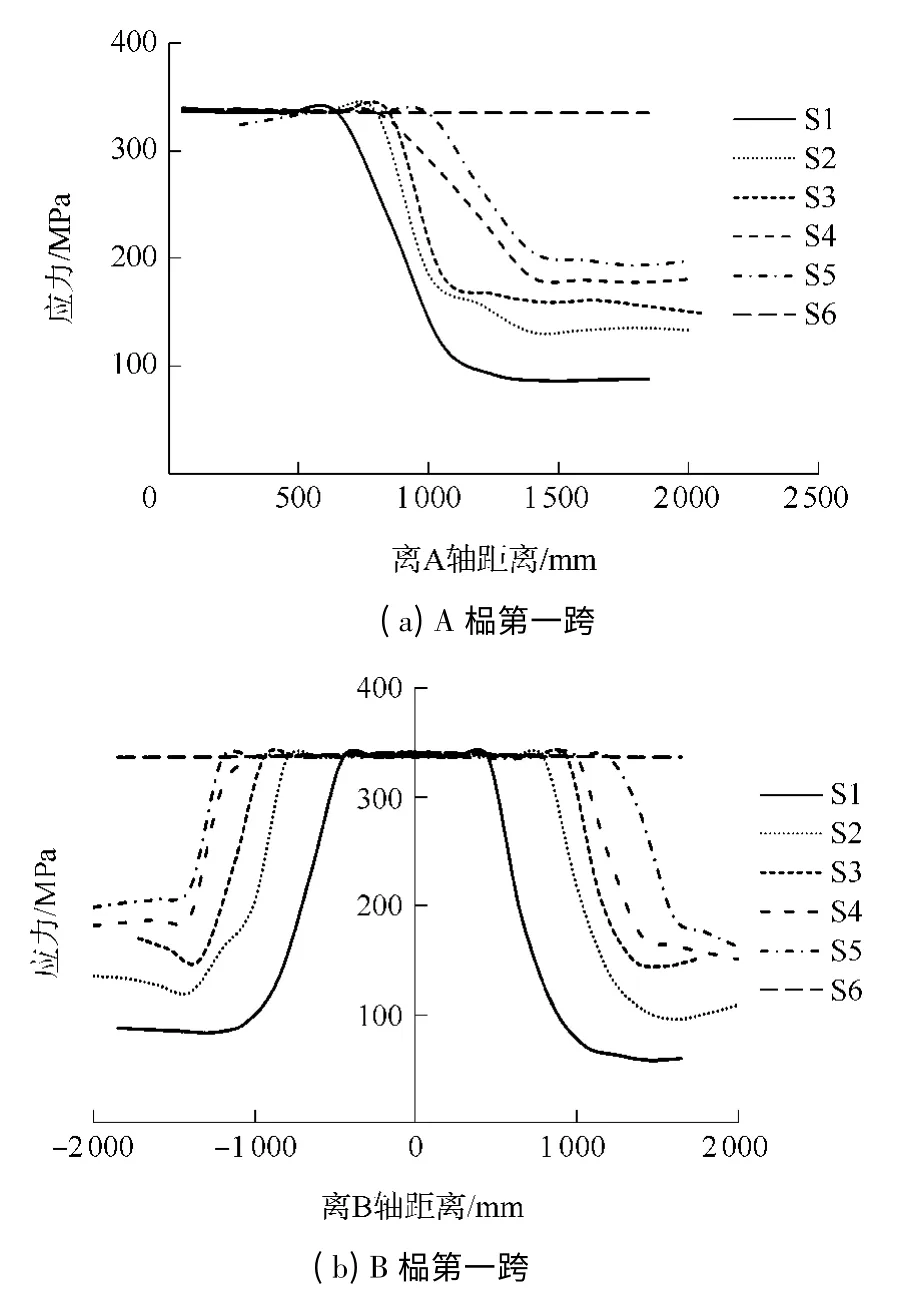
图8 板面筋应力分布Fig.8 Stress distribution of slab reinforcement on the top

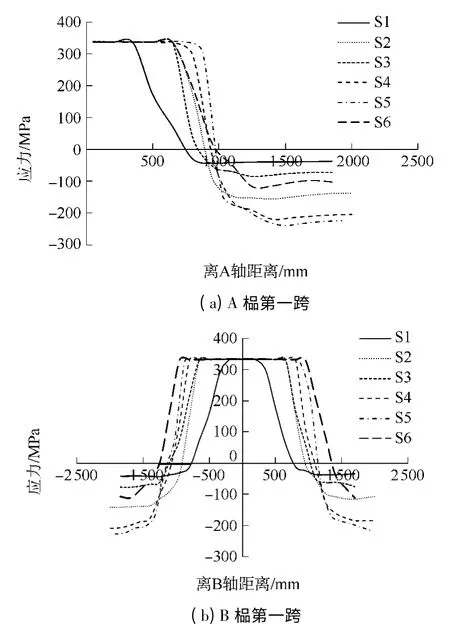
图9 板底筋应力分布Fig.9 Stress distribution of slab reinforcement at the bottom

4 有效翼缘宽度回归公式

由于同一结构中，边榀和中间榀的框架以及边节点(柱端单侧与框架梁相连)和中节点(柱端两侧与框架梁相连)处的板筋参与作用均不同［15，21］，因此在对有效翼缘宽度进行数值回归时需根据节点类型分开进行.根据式(1)计算S1－S6 模型各节点处框架梁负弯矩端的有效翼缘宽度，结果见表2.

定义μ为有效翼缘宽度bf与正交梁净跨ln的比值，图10 给出了S1－S6 模型的μ-n 关系曲线.

表2 模型的有效翼缘宽度Table 2 Effective flange width of the models mm

图10 μ-n 关系曲线Fig.10 μ-n curves

对图10 的曲线进行数值回归，并对多种拟合结果进行评估对比.表3 列出了边榀框架的回归曲线对比.综合对比可得三次曲线形式最佳，因此1/50层间位移角时的有效翼缘宽度bf简化公式如式(5)－(8)所示.

边榀边节点:

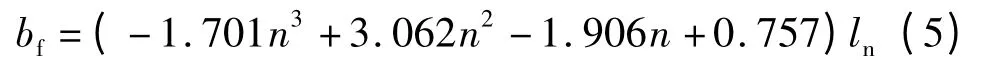
边榀中节点:

中间榀边节点:

中间榀中节点:

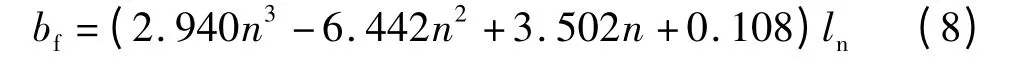
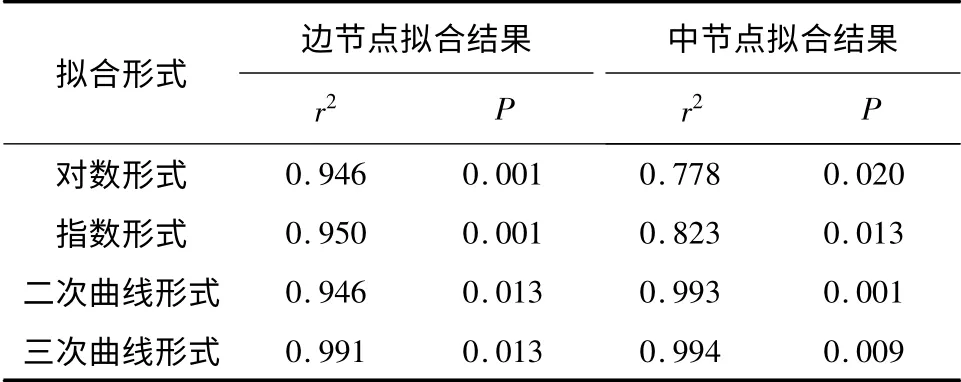
表3 边榀框架拟合结果对比1)Table 3 Comparison of fitting results of exterior frame

5 改进设计建议

由已有研究［21］可知:在达到1/50 层间位移角之前，板筋应力随侧向位移增加而明显增大;达到1/50 层间位移角后，板筋应力随侧向移增长缓慢，且当达到1/50 层间位移角限值时，结构的承载能力－位移曲线开始进入下降段.因此，考虑板筋对框架梁端抗弯能力的影响后，若要达到“大震不倒”的设防目标，必须使RC 框架在1/50 层间位移角时，同一节点处的柱端实际承载力大于框架梁实际承载力与板筋已发挥出的参与抗弯能力之和，保证柱顶钢筋比考虑到了板筋参与作用后的框架梁端纵筋晚屈服，用公式表示即为

式中，∑Mcua的定义同现行混凝土结构设计规范［22］，∑Mbua为同一节点左右梁端矩形截面内按实际配筋计算的实际受弯承载力，Ms为负弯矩作用端有效翼缘宽度范围内板筋所承受的弯矩.参与抗弯的板筋面积As按下式计算:

式中，bf按式(5)－(8)计算.

由图10 可知:高轴压比时bf随n 的变化程度较大，说明此时通过降低结构轴压比来实现“强柱弱梁”能收到较好效果;而低轴压比时bf随n 的变化程度减缓，结合第3 节板筋应力分布可知，这是由于低轴压比时能参与作用的板筋基本都已发挥作用，bf趋于上限值，因而此时若再通过降低结构轴压比来实现“强柱弱梁”，效果并不明显，更好的方式是加强柱内配筋、增大柱端实际承载力.因此验算过程中若不满足式(9)，则应结合轴压比n 分情况处理:

方法1 若n 处于高轴压比区，则适当增大柱截面、降低n 后重新验算式(9)，此为通过改变bf来实现式(9);亦可通过加强柱内配筋进行调整，两种方式可结合经济性进行选择.

方法2 若n 处于低轴压比区，则加强柱内配筋后重新验算式(9)，此为通过增大柱端实际承载力实现式(9).

6 工程实例验证

文中以某8 层RC 规则框架为例进行验证.框架的平面和立面布置分别如图11 和12 所示.该框架为7 度设防，Ⅱ类场地，设计地震分组为第一组.柱截面尺寸为400 mm ×400 mm;梁截面尺寸为:Y 向梁200 mm ×600 mm、X 向梁200 mm ×500 mm;板厚为100 mm.楼面恒载取为3.5 kN/m2，活荷载取为2.0 kN/m2;梁上墙载取为:外墙9.0 kN/m、内墙5.8 kN/m;基本风压为0.50 kN/m2.

图11 框架结构平面图(单位:mm)Fig.11 Layout of the frame structure (Unit:mm)

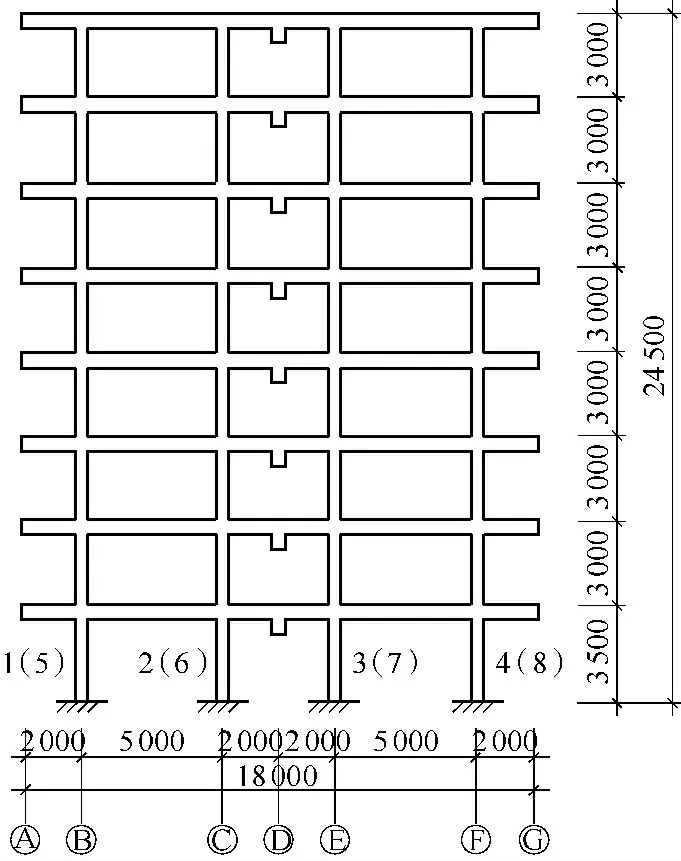
图12 框架结构立面图(单位:mm)Fig.12 Elevation of the frame structure (Unit:mm)

混凝土强度等级为C30，梁、板、柱构件受力筋采用HRB335 钢筋，箍筋采用HPB300 钢筋.各构件配筋均满足现行结构设计规范，底层梁端实配钢筋见表4，板面筋为φ8@150(φ 仅代表直径)、板底构造配筋，柱截面配筋为8φ16(对称配筋).

表4 梁端实配钢筋面积Table 4 Actual reinforcement area of beam end mm2

按第5 节的改进设计建议进行验算，图11 边榀和中间榀框架的验算结果见表5.由表5 可知，考虑板筋的参与作用后，中间榀框架的5、6 号柱不能满足式(9)的验算要求.5、6号柱属于高轴压比区，因此采用改进设计建议中的方法1 进行调整:增大柱截面尺寸至450 mm ×450 mm、降低轴压比、不改变配筋，重新验算后的结果见表6，调整后各节点均满足式(9)，调整后柱截面混凝土用量仅比原来增加12.5%.可见文中建议的有效翼缘宽度简化公式和改进设计建议在实际设计中具有可行性，且应用简便.

表5 初始设计框架节点的验算结果Table 5 Checking results of the joints with initial frame dimension

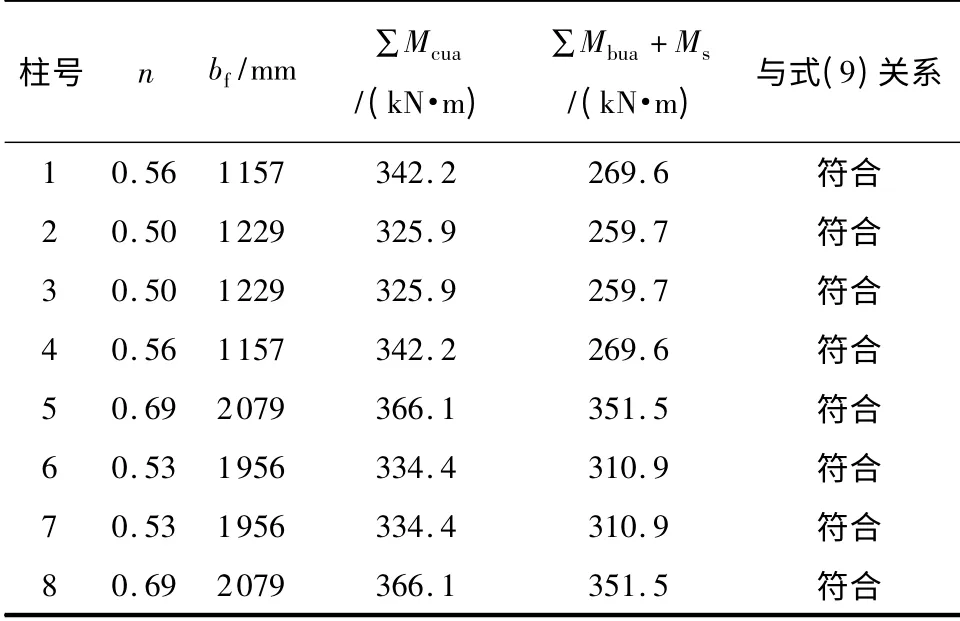
表6 修改后的框架节点验算结果Table 6 Checking results of the joints with amended frame dimension

7 结语

文中结合现浇楼板内的板筋应力分布情况和有效翼缘宽度的理论计算方法，对0.3～0.9 轴压比范围内的规则框架有效翼缘宽度分布规律进行了数值回归，得到了更方便用于实际结构设计的有效翼缘宽度简化公式.同时，结合有效翼缘宽度和轴压比分布，给出了能更好地实现“大震不倒”设防目标的改进设计建议，并对有效翼缘宽度简化公式和改进设计建议进行了实际工程验证.在后续研究中将开展足尺RC 空间框架的试验研究，进一步明确板筋在框架梁端抗弯能力中的参与作用和参与方式，并将用有效翼缘宽度来考虑板筋参与作用的RC 框架抗震性能与按现行规范设计的进行对比，为有效翼缘宽度取值方法的明确和统一提供试验和理论参考.

［1］吴波，王明君.混凝土空间板柱结构的震致落层倒塌分析［J］.华南理工大学学报:自然科学版，2012，40(2):1-6.Wu Bo，Wang Ming-jun.Analysis of pancake collapse of RC space slab-column structures under earthquake［J］.Journal of South China University of Technology:Natural Science Edition，2012，40(2):1-6.

［2］Bin Z，Fabio T，Tiziana R.Field investigation on the performance of building structures during the 12 May 2008 Wenchuan earthquake in China［J］.Engineering Structures，2009，31(8):1707-1723.

［3］公茂盛，杨永强，谢礼立.芦山7.0 级地震中钢筋混凝土框架结构震害分析［J］.地震工程与工程振动，2013，33(3):20-26.Gong Mao-sheng，Yang Yong-qiang，Xie Li-li.Seismic damage to reinforced concrete frame buildings in Lushan M7.0 earthquake［J］.Journal of Earthquake Engineering of Engineering Vibration，2013，33(3):20-26.

［4］Alemdar B，Ahmet C A，Mevlüt P.Performance and damages of reinforced concrete buildings during the October 23 and November 9，2011 Van，Turkey，earthquakes ［J］.Soil Dynamics and Earthquake Engineering，2013，53(10):49-72.

［5］杨小卫，王亚勇.考虑板筋参与梁端承载力贡献的设计方法及抗震性能研究［J］.建筑科学，2011，27(7):11-16.Yang Xiao-wei，Wang Ya-yong.Study on design method and seismic performance in consideration of the contribution of rebar in slabs to the bearing capacity of beams［J］.Building Science，2011，27(7):11-16.

［6］杨红，朱振华，白绍良.双向地震作用下我国“强柱弱梁”措施的有效性评估［J］.土木工程学报，2011，44(1):58-64.Yang Hong，Zhu Zhen-hua，Bai Shao-liang.An evaluation of the effectiveness of the Chinese strong column weak beam measure under bi-directional horizontal seismic excitations［J］.China Civil Engineering Journal，2011，44(1):58-64.

［7］王素裹，韩小雷，季静.现浇楼板对RC 框架结构破坏形式的影响分析［J］.土木建筑与环境工程，2009，31(1):66-71.Wang Su-guo，Han Xiao-lei，Ji Jing.The effect of slabs on the failure mode of reinforced concrete frame structures［J］.Journal of Civil，Architectural ＆ Environmental Engineering，2009，31(1):66-71.

［8］王素裹.结构整体效应对RC 框架结构屈服机制的影响(一):数值分析［J］.重庆大学学报，2013，36(10):126-132.Wang Su-guo.Research on the influence of structure integral performance to the RC frame structure failure mode(Ⅰ):numerical analysis［J］.Journal of Chongqing University，2013，36(10):126-132.

［9］NZS 3101，Concrete Structures Standard［S］.

［10］ACI Committee 318.Building code requirements for structural concrete (ACI 318-11)and commentary ［S］.Farmington Hills:American Concrete Institute，2011.

［11］CEN.Eurocode 8:design of structures for earthquake resistance—part 1:general rules，seismic actions and rules for buildings ［S］.Bruxelles:European Committee for Standardization，2004.

［12］GB 50011—2010，建筑抗震设计规范［S］.

［13］吴勇，雷汲川，杨红，等.板筋参与梁端负弯矩承载力问题的探讨［J］.重庆建筑大学学报，2002，24(3):33-37.Wu Yong，Lei Ji-chuan，Yang Hong，et al.Discussion on negative flexural strength of beams including slabs［J］.Journal of Chongqing Jianzhu University，2002，24(3):33-37.

［14］Ehsani M R，Wight J K.Behavior of external reinforced concrete beam to column connections subjected to earthquake type loading［R］.Ann Arbor:University of Michigan，1982.

［15］Ning Ning，Qu Wenjun，Zhu Peng.Role of cast-in situ slabs in RC frames under low frequency cyclic load［J］.Engineering Structures，2014，59(2):28-38.

［16］王素裹，韩小雷，季静，等.不同轴压比下RC 框架结构“强柱弱梁”设计准则的实现［J］.世界地震工程，2010，26(3):96-101.Wang Su-guo，Han Xiao-lei，Ji Jing，et al.The influence of axial compression ratios on the strong-column and weak-beam actualization of RC frames ［J］.World Earthquake Engineering，2010，26(3):96-101.

［17］Masi A，Santarsiero G，Nigro D.Cyclic tests on external RC beam-column joints:role of seismic design level and axial load value on the ultimate capacity［J］.Journal of Earthquake Engineering，2012，17(1):110-136.

［18］Masi A，Santarsiero G，Lignola G P，et al.Study of the seismic behavior of external RC beam-column joints through experimental tests and numerical simulations［J］.Engineering Structures，2013，52(7):207-219.

［19］French C W，Moehle J P.Effect of floor slab on behavior of slab-beam-column connections ［J］.ACI Structural Journal SP-123，1991:225-258.

［20］郑士举，蒋利学，张伟平.现浇混凝土框架梁端截面有效翼缘宽度的试验研究与分析［J］.结构工程师，2009，25(2):134-140.Zheng Shi-ju，Jiang Li-xue，Zhang Wei-ping.Experimental research and analysis of effective flange width of beam end section in cast-in-situ concrete frame ［J］.Structural Engineers，2009，25(2):134-140.

［21］王素裹.强震作用下现浇RC 楼板对框架结构破坏形态影响的研究［D］.广州:华南理工大学土木与交通学院，2009.

［22］GB 50010—2010，混凝土结构设计规范［S］.