基于相平面法的车辆行驶稳定性判定方法*

刘飞 熊璐，2 邓律华，2 冯源，2 邬肖鹏

(1.同济大学 汽车学院，上海 201804;2.同济大学 新能源汽车工程中心，上海 201804;3.上海汽车集团股份有限公司 技术中心，上海 201804)

主动安全性一直以来都是汽车底盘控制领域重要的研究课题.目前，比较成熟的汽车主动安全技术包括:制动防抱死系统(ABS)、牵引力控制系统(ASR)、电子稳定性程序(ESP)等［1］.其中，在对ESP 等电子控制系统的研究以及开发过程中，分析车辆行驶的稳定性并建立相应的判定方法，无论是在策略开发初期对汽车失稳数据的收集还是在稳定性控制策略设计阶段都是必不可少的.

在对车辆进行稳定性分析的研究中，出现过两类方法:一类是基于李雅普诺夫稳定性第二定理的方法［2-6］，另一类则借助了相平面这一工具［7］.

二阶系统可以很直观地从相平面上对车辆进行稳定性分析.某车辆行驶的相平面显示，车辆的失稳与鞍点密切相关，在前轮转角达0.015 rad 时，车辆状态变量向量场的特性发生较大变化，即出现鞍点分岔现象，而车辆是否稳定与此紧密相关［8-9］.

郭孔辉［10］通过能量相平面法，采用转弯动能与前进动能之比来评价转向性能，从能量角度说明了车辆的失稳.John 和Jeffrey［11］利用侧向加速度与横摆角速度建立相平面，通过切点法和逆轨迹法找到确定侧向稳定区域的边界.Young 等［12］在此基础上引入了拓扑学来界定车辆的侧向稳定区域，并通过对平衡点的局部线性化建立了简易的稳定性判据.Shoji 等［13］利用车辆质心侧偏角及质心侧偏角速度构建β-相平面来对车辆行驶的侧向稳定性进行分析，认为β-相平面比由车辆质心侧偏角与横摆角速度构成的β-相平面更适合分析车辆行驶的侧向稳定特性.张晨晨等［14］认为相平面稳定区域为两条平行斜线之间的平行区域，并分析了速度、附着系数以及转向盘转角对斜线的影响.Taeyoung 等［15］认为β-相平面中的稳定区域可以用一个菱形来表示，菱形的左、右顶点为相图的鞍点，上、下端点在坐标轴上.Anne 等［16］通过仿真验证了文献［15］中方法的工作效果，但该方法在某些情况下找不到上、下端点.

1 仿真模型的构建

为便于后续研究，文中建立了与实车相应的仿真模型(参数见表1)，通过相关的车辆试验获取了实车试验平台电动车的参数以及车辆侧向特性数据，对前、后轴侧偏特性进行了拟合(结果见图1)，采用简化的魔术公式［17］建立轮胎模型，前、后轴侧向力拟合公式分别如式(1)和(2)所示:

式中，μ 为路面附着系数，Fz，f和Fz，r分别为前、后轴的垂向力，αf和αr分别为此时前、后轴的侧偏角.之后，根据得到的车辆参数，在Matlab/Simulink 仿真环境下建立车辆非线性单轨模型，并在Carsim 动力学仿真软件中建立与电动车试验平台相应的仿真模型，最后在典型的试验工况下对仿真模型进行验证.

表1 仿真车辆模型的部分参数Table 1 Partial vehicle parameters of simulation model

为验证所建立的仿真模型的正确性，文中设计了蛇行试验.从模型响应与实车试验数据对比(见图2)中可以看出，仿真模型的横摆角速度和侧向加速度能很好地与实车吻合，可以用于相平面分析.

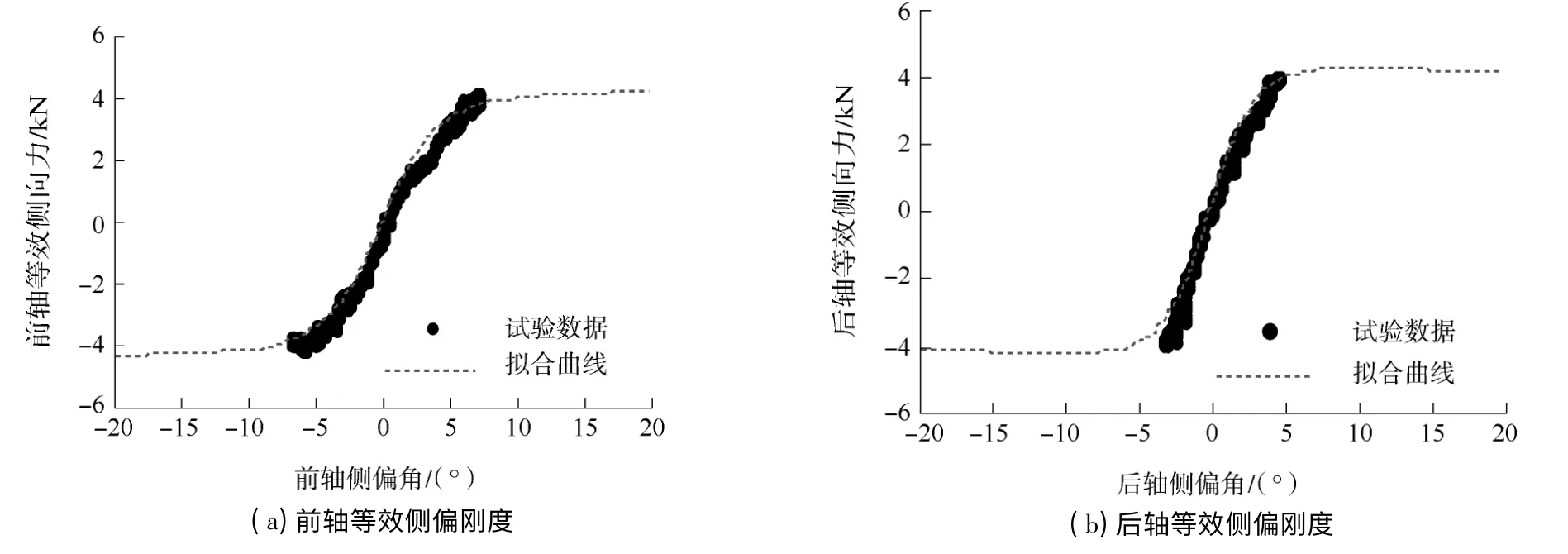
图1 前、后轴等效侧偏特性曲线Fig.1 Equivalent cornering characteristic curves of front and rear axes

图2 蛇形工况下仿真与实车试验数据对比Fig.2 Comparison between simulated results and real-vehicle test data under snake-shaped condition

2 相图的建立

2.1 相平面分析方法的基础

二阶自治系统可由2 个标量微分方程表示:

令x(t)=(x1(t)，x2(t))是方程(3)和(4)的解，初始状态为x0(x1(0)，x2(0))，对于所有时刻t(t≥0)，x(t)的解在x1-x2平面的轨线是一条通过x0点的曲线，该曲线称为方程(3)和(4)始于x0点的轨线或轨道.x1-x2平面通常称为状态平面或相平面.

相轨迹在相平面上任意一点的斜率为

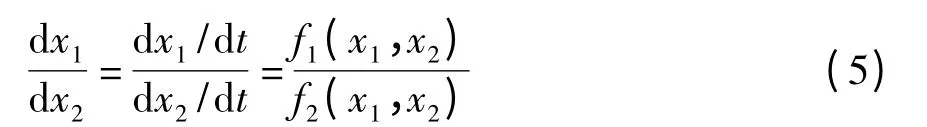
根据非线性单轨车辆模型的动力学分析，若前轮转角固定，其微分方程如式(6)和(7)所示:

式中，k1、k2分别为前、后轴等效侧偏刚度，vx为纵向车速，δf为前轮转角.

式(6)和(7)可以表示为如式(8)和(9)所示的二阶自治系统:

2.2 质心侧偏角－质心侧偏角速度相图

研究车辆稳定性时，质心侧偏角β 是研究的重点［14］.根据前面建立的非线性车辆单轨模型，在确定的纵向车速vx、路面附着系数μ 和前轮转角δf下，只需绘制不同初始值(β(0)，(0))下系统的相轨迹，便可得到车辆的相图.

图3 β-相图Fig.3 β-phase plane

图3 是vx为70 km/h、μ 为1.0、前轮转角δf为0°时的β-相图.图中实线为收敛到稳定点的轨迹线，虚线为无法收敛到稳定点的轨迹线(下文的相图均采用此方法区分轨迹线)，三角形标识为该相图的鞍点.在该相图中，黑色轨迹线区域为相平面的稳定区域，表示车辆的自治系统在该区域均能收敛到稳定点.

3 稳定区域的划分及变化

3.1 稳定区域的划分

文献［12］提出了双线法来划分稳定区域，如图4所示，但这种方法存在一个弊端——只要侧偏角速度足够小，即使侧偏角很大，车辆也是稳定的.

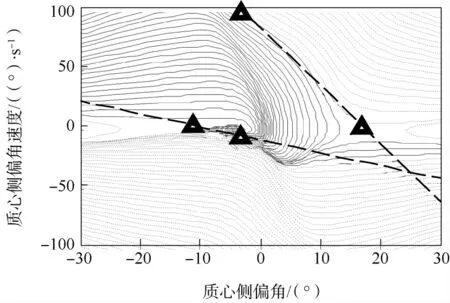
图4 双线法定义的β-相图稳定区域Fig.4 Stability region in β- phase plane defined via double line method

图5 所示为vx=70 km/h、μ=1.0、δf=8°时的β-相图.可以看出，当稳定区域极小时，双线法并不适合用来划分稳定区域.

文献［13］中提出了菱形法来划分稳定区域，如图6 所示.该方法所采用的菱形的上、下端点在坐标轴上，但从图5 所示的相图来看，采用这种方法可能会出现找不到菱形上、下端点的情况.因此，文中采用改进的五特征值菱形法划分稳定区域，使菱形上下端点的β 值与稳定点的相同(结果见图7).文中方法确定的菱形需要记录5 个参数的位置，分别为左、右端点的β 值，上、下端点的值以及平衡点的β 值，因此可以避免前述双线法和菱形法的局限，并用统一的方法准确地确定相图的稳定区域.

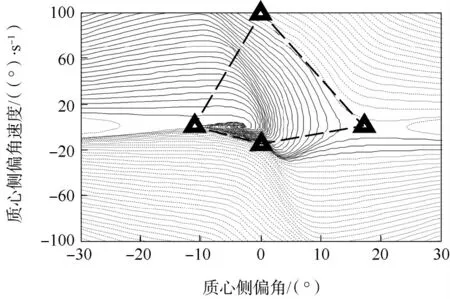
图6 菱形法定义的β-相图稳定区域Fig.6 Stability region in β- phase plane defined via diamond method

图7 改进的五特征值菱形法确定的稳定区域Fig.7 Stability region defined via advanced five-characteristicvalue diamond method

3.2 稳定区域特征值的确定方法

表2 3 个变量的变化范围及变化步长Table 2 Variation range and step of three variables

图8(a)－8(f)分别示出了车速为20，30，…，70 km/h时质心侧偏角稳定值随路面附着系数、前轮转角的变化规律.

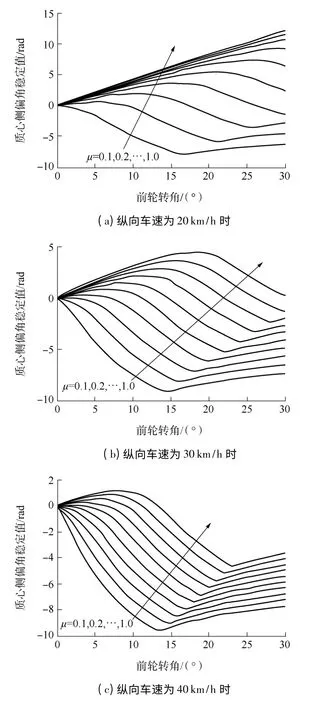
图8 质心侧偏角稳定值的变化规律Fig.8 Variation of stability point of sideslip angle

从图8 可以看出:曲线在垂向的分布比较均匀，因此路面附着系数划分为0.2、0.4、0.6、0.8、1.0共5 个样点;质心侧偏角稳定值的拐点处于5°～15°之间，故前轮转角划分为0°、5°、10°、15°、20°、30°共6 个样点.从图8 还可看出，对应于20～50 km/h 速度区间的质心侧偏角稳定值的变化趋势有比较大的差异，纵向车速大于50 km/h 后，质心侧偏角稳定值的变化趋势比较相似.因此，将纵向车速划分为20、30、40、50、70 km/h 共5 个样点.

根据前面划分的vx、μ 及δf样点，可得到150(5 ×5 ×6=150)个样工况.在Matlab 环境下绘制样工况下的β-相平面图，然后根据上述的菱形稳定区域确定方法获取其5 个特征值，这些菱形特征值组成了全工况下稳定区域的查表数据库.

3.3 相图菱形稳定区域的变化规律

图9－12分别表示纵向车速vx为40km/h时菱形各端点位置随μ 和δf的变化.可以看到，菱形右端点随着δf的增大先向右移动，后迅速向左移动，直至失去稳定.菱形上端点的变化规律与右端点的相似，先向上移动，再迅速靠近横轴.与前面两个端点不同，菱形下端点始终单调地往横轴靠近，而左端点没有很明显的变化，只是整体趋势在往右移动，这是由于左端点并非左鞍点，在相图流形发生变化之后，其与左鞍点的相对位置也会跟着变化.

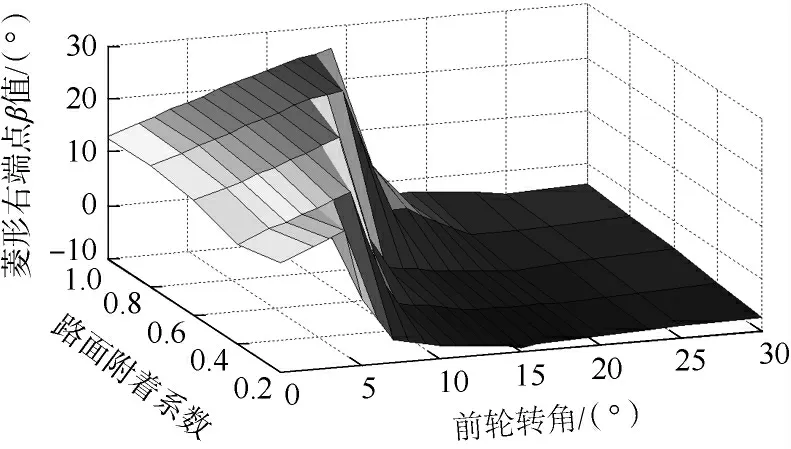
图9 纵向车速vx 为40 km/h 时菱形右端点的变化Fig.9 Variation of diamond right point when vx is 40 km/h

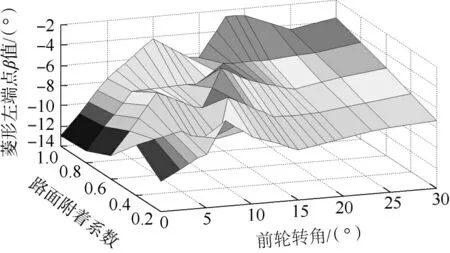
图10 纵向车速vx 为40 km/h 时菱形左端点的变化规律Fig.10 Variation of diamond left point when vx is 40 km/h

图11 纵向车速vx 为40 km/h 时菱形上端点的变化规律Fig.11 Variation of diamond up point when vx is 40 km/h

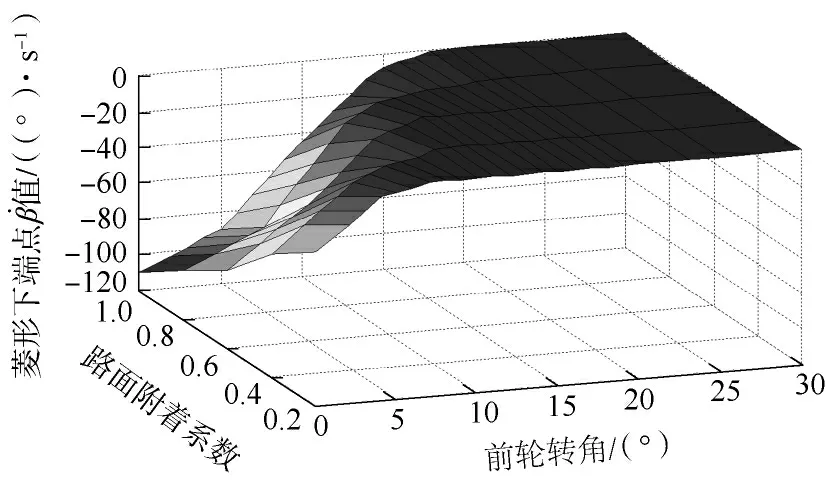
图12 纵向车速vx 为40 km/h 时菱形下端点变化规律Fig.12 Variation of diamond bottom point when vx is 40 km/h

图13 所示为相同车速和前轮转角下菱形稳定区域随路面附着系数的变化.可以看出，随附着系数的增大，稳定区域变大，当附着系数为0.2 时，菱形稳定区域为图中的一个点.

图13 菱形稳定区域随路面附着系数的变化Fig.13 Variation of diamond stability region with road adhesion coefficient

图14 所示为相同车速和路面附着系数下菱形稳定区域随前轮转角的变化.由图可知:随着前轮转角的增大，稳定区域往转向方向偏移;当方向盘为正的时候，菱形4 个端点开始往右(β 为正)方向偏移，上下端点同时往上(为正)方向偏移.从菱形形状来看，以稳定点的位置来分割，右侧区域增大，而左侧区域缩小.但当前轮转角增大到一定程度后，稳定区域开始缩小，直至完全消失，图中前轮转角为30°时，稳定区域为图中一个点.

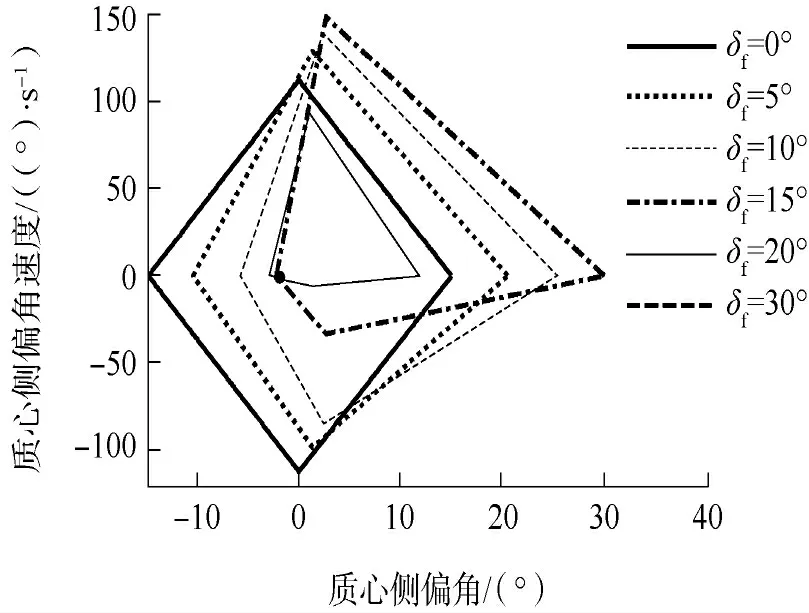
图14 菱形稳定区域随前轮转角的变化Fig.14 Variation of diamond stability region with front wheel angle

4 车辆稳定性控制的仿真分析

4.1 基于相平面法的稳定性判定方法

如图15 所示，结合前面所建立的数据库，可以确定基于相平面法的车辆操纵稳定性判定方法.该判定方法需要输入vx、μ、δf、β、信号.从普通车辆的传感器配置来看，vx可以通过估计得到，δf可以通过传感器获取，而μ 和β 需要进行辨识，这里不对此部分内容进行阐述.稳定区域的5 个特征值通过纵向车速、路面附着系数和前轮转角来进行离线查值得到，然后再实时判断所辨识的质心侧偏角和质心侧偏角速度是否在菱形区域内，在则判定车辆处于稳定区域，不在则判定车辆处于失稳状态.

图15 基于相平面法的稳定性判定方法示意图Fig.15 Schematic diagram of stability criterion based on phase plane method

4.2 结合稳定性判定方法的稳定性控制仿真

将基于相平面法的稳定性判定方法的判定结果作为稳定性控制策略的介入依据，结合已有的稳定性控制进行仿真分析，在Matlab/Simulink 环境下建立了四轮驱动电动车的Carsim 仿真模型，选用的车辆模型参数列于表1，仿真工况为ISO 3888-2:2002 避障工况，车速为60 km/h，路面附着系数为0.8.车辆的控制算法结构如图16 所示.图中，稳定性控制只有在介入判断成立时才起作用，其余时间则主要通过操纵改善控制模块来分配4 个车轮的转矩.

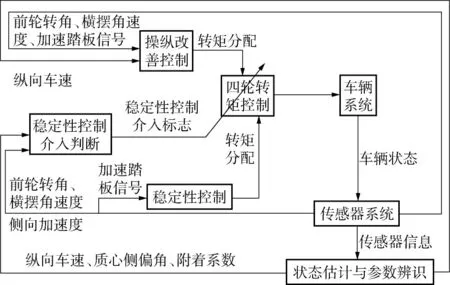
图16 车辆稳定性控制算法的结构Fig.16 Algorithm frame of vehicle stability control

施加控制与未施加控制车辆通过工况的情况对比如图17 所示，图中空心小圆圈为控制算法的介入时刻，控制算法是否介入由稳定性判据给出.未施加控制的车辆在通过工况时出现了明显的甩尾和碰桩，未能通过工况;施加控制的车辆在跟踪理想轨线的同时保持了良好的车身姿态，安全通过了工况.

图17 ISO 双移线仿真结果Fig.17 Simulation results of ISO double lane change

由图17 可知，以前述稳定性判定方法的判定结果作为介入控制依据，在车辆进入失稳状态时将稳定性算法介入，可以提高车辆稳定性，使车辆保持稳定性状态下原有的特性，同时避免因稳定性算法过多介入控制而改变驾驶员的操纵感觉.

5 结语

文中提出了改进的五特征值菱形稳定区域划分方法，分析表明，该方法能比原有的菱形法和双线法更准确地表示相图的稳定区域.文中还提出了确定菱形稳定区域特征值的方法，建立了全工况下质心侧偏角－质心侧偏角速度相图的稳定区域特征值数据库，并分析了特征值及稳定区域的变化规律.仿真结果表明，基于相平面分析的车辆稳定性判定方法可以为稳定性控制策略介入控制提供准确的依据，提高车辆稳定性.

然而，文中对判据工作效果的对比及评价是通过大量仿真试验得到的，后续研究中，需对文中提出的稳定性判据和控制算法进行相应的改进，并进行实车试验验证.

［1］汽车主动安全技术编委会.世界汽车主动安全技术文献选编［M］.北京:科学技术文献出版社，2008:1-13.

［2］Chou Sachs.On the stability in the sense of liapunov of a rubber tire vehicle ［J］.Journal of Dynamic Systems，Measurement，and Control，1976，98(1):180-185.

［3］杨秀建，王增才.汽车稳态转向失稳的最近分叉点实时追踪［J］.农业机械学报，2009，40(1):21-25.Yang Xiu-jian，Wang Zeng-cai.Real-time tracking of the closest bifurcation for vehicle steady-state corning stability［J］.Transaction of the Chinese Society for Agricultural Machinery，2009，40(1):21-25.

［4］杨秀建.极限工况下汽车转向失稳的非线性动力学特性与主动控制研究［D］.济南:山东大学机械工程学院汽车工程系，2009.

［5］杨秀建，王增才.极限工况下周期转向汽车侧向动力稳定性及分岔分析［J］.公路交通科技，2009，26(11):141-145，152.Yang Xiu-jian，Wang Zeng-cai.Analysis on lateral dynamic stability and bifurcation of vehicle periodic steering under critical condition ［J］.Journal of Highway and Transportation Research and Development，2009，26(11):141-145，152.

［6］毛振勇.车辆转向稳定性的势能分析方法研究［D］.长春:吉林大学汽车工程学院，2003.

［7］刘伟.基于质心侧偏角相平面的车辆稳定性控制系统研究［D］.长春:吉林大学汽车工程学院，2013.

［8］Hale J K，Kocak Hüseyin.Dynamics and bifurcations［M］.New York:Springer-Verlag，1991.

［9］Eiichi Ono，Shigeyuki Hosoe，Hoang D Tuan，et al.Bifurcation in vehicle dynamics and robust front wheel steering control［J］.IEEE Transactions on Control Systems Technology，1998，6(3):412-420.

［10］郭孔辉.识别汽车方向控制特性的能量相平面表示方法［C］∥1984年长春汽车研究所学术交流会论文汇编.长春:中国汽车工业公司，1985.

［11］John S，Jeffrey C H.Estimating lateral stability region of nonlinear 2 degree-of-freedom vehicle ［C］∥Proceedings of International Congress and Exposition.Detroit:SAE，1998:1-7.

［12］Young E K，Jang M L.Estimation of the stability region of a vehicle in plane motion using a topological approach［J］.International Journal of Vehicle Design，2002，30(3):181-192.

［13］Shoji Inagaki，Ikuo Kshiro，Masaki Yamamoto.Analysis on vehicle stability in critical cornering using phaseplane method［J］.JSAE Review，1995，16(2):287-292.

［14］张晨晨，夏群生，何乐.质心侧偏角对车辆稳定性影响的研究［J］.汽车工程，2011，33(4):277-282.Zhang Chenchen，Xia Quansheng，He Le.A study on the influence of sideslip angle at mass center on vehicle stability［J］.Automotive Engineering，2011，33(4):277-282.

［15］Taeyoung C，Kyongsu Y.Design and evaluation of side slip angle-based vehicle stability control scheme on a virtual test track ［J］.IEEE Transactions on Control Systems Technology，2006，14(2):224-234.

［16］Anne V V，Lu Haiyan，Uwe Kiencke.Detection of critical driving situations using phase plane method for vehicle lateral dynamics control by rear wheel steering［C］∥Proceedings of the 17th World Congress，IFAC.Seoul:Elsevier，2008:5694-5699.

［17］Pacejka H B.Tyre and vehicle dynamics［M］.Oxford:Butterworth-Heinemann，2002.