AP1000设计基准事故试验热冲击过程数值模拟

郑开云， 葛 磊， 陈功名， 王兴平

（上海发电设备成套设计研究院，上海 200240）

核电厂安全级设备需要通过一系列的鉴定试验，以验证设备安全相关功能满足设计规范要求.设计基准事故（DBA）模拟试验通常是设备鉴定中的最后一项试验，用于模拟核电厂失水事故（LOCA）、主蒸汽管道破裂（MSLB）或高能管道破裂（HELB）事故，试验依据核电厂设计规范书或者鉴定试验标准中给出的DBA温度和压力曲线进行.根据核电设备鉴定试验要求，实际的DBA试验温度和压力条件必须包络要求的试验曲线并加上规定裕度［1］.

DBA试验热冲击过程是整个试验的关键环节之一，这一过程模拟了核电厂管道破裂的瞬间［2］.对于国内基于法国M310堆型的二代核电厂，核电设备DBA试验遵循法国标准NFM61－001规定试验曲线，有2次热冲击，均要求在30s内温度从323.2 K上升到429.2K，压力从0.100MPa上升到0.560 MPa［3］.对于目前正在建设的三代AP1000核电厂，DBA热冲击过程要求在第1s内温度从324.9K上升到421.8K（包括8K裕度），压力从0.122MPa上升到0.177MPa，到第19s时温度达到峰值497.9K（包括8K裕度），压力达到0.536MPa（包括0.069MPa裕度）.三代核电DBA试验热冲击速率高于二代核电，尤其是第1s热冲击温升接近100 K，对试验装置的能力提出更高要求，用于核电设备DBA鉴定试验的装置需要重新设计或改造.

DBA试验装置（LOCA炉）的热力系统核心部件包括蒸汽源、储汽罐（组）、试验仓、快开阀和连接管道等，基本工艺过程为：事先将高温高压蒸汽储存于储汽罐，试验时打开快开阀，储汽罐中的蒸汽快速充入试验仓中［2，4-5］.对于 AP1000核电设备的 DBA试验来说，第1s热冲击过程的试验难度最高，储汽罐必须在1s内提供蒸汽和能量使试验仓从初始温度和压力（324.9K／0.122MPa）达到目标温度和压力（421.8K／0.177MPa）.试验装置的系统设计必须解决以下技术难题：储汽罐能够在1s内将所需的蒸汽质量和能量传输至试验仓内，同时至少确保试验仓内试件周围介质（空气和蒸汽）的温度和压力在1s内达到目标值.此外，测量系统也应能够准确测量热冲击过程的温度和压力变化，特别是温度测量系统的响应应足够快［2］.

由于1s瞬态过程难以通过常规的热工方法进行测量，需要结合理论计算和计算机模拟的方法加以分析.随着计算流体动力学（CFD）及相应计算机软件技术的发展，数值模拟计算广泛应用于流体力学问题的研究，其中刘强等［6］采用CFX软件对二代核电DBA试验热冲击过程进行了数值模拟.笔者试图应用Fluent软件模拟AP1000核电DBA试验第1s热冲击过程，通过数值计算获得热冲击瞬态物质和能量传输过程以及系统温度、压力、流速和组分质量分数等状态参数的变化，探讨实现1s内瞬态热冲击试验的技术可行性，从而为AP1000核电DBA试验装置的设计和试验工艺的制定提供参考依据.

1 物理模型与热力学计算

1.1 物理模型

图1是简化的DBA试验装置物理模型，为简化数值模拟计算，物理模型设为轴对称几何结构，包括2个储汽罐（容积各0.52m3）、试验仓（容积17.18 m3）及仓内试件（体积1.41m3）、连接管道（内径60 mm）和快开阀.根据前人研究经验［2］，储汽罐用来存储过热蒸汽，温度不超过安全壳主工艺系统介质温度（＜623.2K）.为确保储汽罐有足够的充气能力并考虑压力容器设计，采用2MPa左右的压力较为合理.储汽罐容积仅考虑第1s热冲击的蒸汽供应量，分别布置于试验仓两端.快开阀启动至全开时间设为0.5s，内径设为60mm，以符合现有快开阀技术水平.

图1 DBA试验装置物理模型Fig.1 Physical model of the DBA testing facility

1.2 热力学计算

物理模型的热力学计算基于以下假设：（1）第1 s结束时储汽罐和试验仓内近似达到热平衡；（2）空气和过热蒸汽状态变化近似服从理想气体状态方程；（3）忽略热冲击过程的热损失，包括储汽罐、试验仓、试件和管道等吸热；（4）能量计算忽略流体的动能.通过试凑法计算可获得试验初始参数，以表1所列初始条件为例，以下给出相应的验算过程.

储汽罐初始温度（T储1）、压力（p储1）、比热力学能（u储1）、密度（ρ储1）、容积（V储）、质量（m储1）以及试验仓初始温度（T试1）、压力（p试1）、比热力学能（u试1）、密度（ρ试1）、容积（V试）、质量（m试1）列于表1.

表1 储汽罐和试验仓的初始条件Tab.1 Initial condition of the accumulator and test chamber

储汽罐快速释放蒸汽为绝热过程，罐内过热蒸汽按定熵过程变化，即

式中：κ为过热蒸汽绝热指数，取κ＝1.3；T储2、p储2分别为储汽罐蒸汽释放过程的温度和压力.

当储汽罐压力降至p储2＝0.900MPa时，储汽罐的温度T储2＝510.0K.此时，储汽罐剩余的蒸汽仍然处于过热状态，比热力学能u储2＝2691kJ／kg，密度ρ储2＝3.97kg／m3，质量m储2＝4.13kg.那么，储汽罐剩余蒸汽的热力学能变化ΔU储＝－628kJ，储汽罐释放的蒸汽质量Δm储＝3.52kg，储汽罐释放蒸汽的初始体积V储放＝0.48m3.

储汽罐释放的蒸汽进入试验仓，与试验仓内空气混合，2种介质均视为理想气体，当试验仓温度（T试2）达到421.8K时，储汽罐释放的蒸汽在试验仓内所达到的分压力p蒸汽为

试验仓内蒸汽的比热力学能u蒸汽＝2584kJ／kg，储汽罐释放的蒸汽的热力学能变化ΔU蒸汽＝－912kJ.试验仓内空气所达到的分压力p空气为

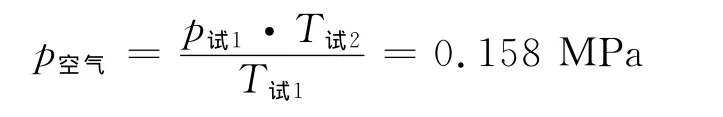
试验仓内空气的比热力学能u空气＝302kJ／kg，空气的热力学能变化ΔU空气＝1446kJ.

储汽罐和试验仓内能量守恒，满足如下公式

则剩余能量ΔU余＝94kJ.表明上述热力学过程还有94kJ能量多余，这些能量还可以使试验仓温度再提高约4.6K，即试验仓最终温度T试2＝426.6 K，试验仓最终压力p试2为

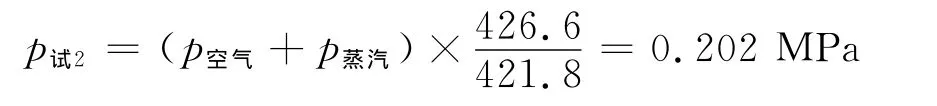
此时，试验仓内介质为未饱和湿空气.

根据以上计算，对于表1给定初始温度和压力，当储汽罐温度和压力为510.0K／0.900MPa时，试验仓可达到的温度和压力为426.6K／0.202MPa，包络预期目标值（421.8K／0.177MPa）.需要说明的是，合理的初始参数可以有很多组，笔者试算了储汽罐温度603～653K和压力1.6～2MPa范围的多组条件，均可以达到预期目标，这里不一一论证.

2 数值模拟

2.1 数值计算模型

根据物理模型的几何对称性，将阀门开启简化为流通孔径扩张过程，数值计算模型可简化为轴对称和镜面对称问题.计算区域取平面几何模型的1／4，采用Gambit的结构化网格划分方法对计算区域进行网络划分.阀门采用动网格，孔径扩张速率为120mm／s，阀门全开时间为0.5s.对初始网格单元数分别为14157、17036和20893三套网格进行了网格无关性验证.网格加密主要针对管道、阀门和试验仓入口至挡板区域，当网格单元数增至20893时，计算结果与前者相比已无显著变化，最终选用此套网格的计算结果.CFD计算通过求解雷诺时均控制方程组，包括连续性方程、组分输运方程、能量方程、动量方程、RNGk－ε湍流模型方程组和理想气体状态方程.

2.2 边界条件和初始条件

储汽罐、试验仓、管道内壁面和试件外壁面、阀门壁面和挡板均设为无滑移绝热固壁边界.阀门左侧区域初始条件定义为613.2K／2.000MPa的静止过热蒸汽，阀门右侧区域初始条件定义为324.9 K／0.122MPa的静止空气.

2.3 求解过程

数值计算采用Fluent的密度基瞬态求解器，隐式求解格式.时间步长取5×10－6s，阀门开启过程每个时间步迭代50次，阀门全开后每个时间步迭代35次，计算结果收敛，累计时间为1s时计算结束.求解过程同时监测系统测点温度、压力、流速、组分质量分数和密度等参数.

3 计算结果及分析

3.1 储汽罐蒸汽状态变化

储汽罐释放蒸汽过程中，除出口处达到亚音速以及轴线附近有一定的速度以外，储汽罐内绝大部分区域的蒸汽接近静止状态.由于储汽罐内蒸汽流速很低，温度、压力和密度的分布都非常均匀.图2为储汽罐内部测点A的温度和压力随时间的变化.由图2可见，随着储汽罐内蒸汽的释放，罐内蒸汽的温度和压力随之降低.在蒸汽释放过程早期（时间＜0.2s），储汽罐内蒸汽温度和压力下降比较缓慢，之后温度和压力开始急剧下降，至0.5s附近下降速率达到最大值，此后温度下降速率基本保持稳定，压力下降速率逐渐减缓.图3为储汽罐内部测点A的温度与压力的关系，对比了数值计算结果与按绝热过程（式（1））的理论计算结果，两条曲线基本重合，说明Fluent数值模拟所采用的网格和求解设置合理，迭代过程充分收敛，数值计算能够准确描述蒸汽释放过程中储汽罐内剩余蒸汽的状态变化.储汽罐中蒸汽释放质量流量通过监测点的密度变化推算.图4给出了储汽罐中蒸汽释放质量流量和累积释放质量随时间的变化.由图4可知，蒸汽释放质量流量先随时间不断升高，至0.5s时达到峰值，正好对应于阀门全开时刻，之后逐渐降低，随着过程的继续，储汽罐累积释放蒸汽质量至0.74s时达到前文热力学估算值3.52kg，由下文分析结果可知，此时试验仓内试件周围环境参数已达到目标值.实际设计时，需考虑流阻的影响，为进一步确保蒸汽瞬时传输至试验仓，可以合理增加蒸汽释放管道.

图2 储汽罐内部测点A的温度和压力随时间的变化Fig.2 Curves of temperature and pressure vs.time for point Ain the accumulator

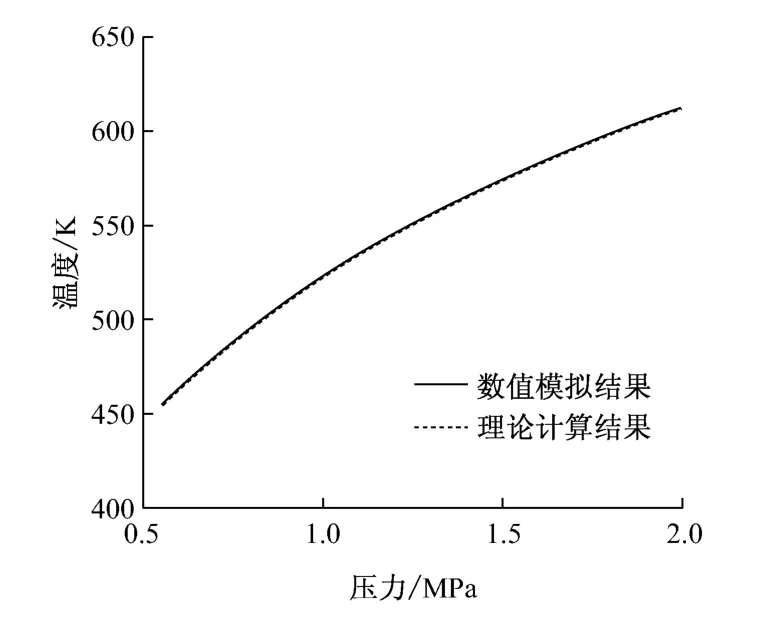
图3 储汽罐内部测点A的温度与压力的关系Fig.3 Relationship between temperature and pressure for point Ain the accumulator

图4 储汽罐中蒸汽释放质量流量和累积释放质量随时间的变化Fig.4 Curves of steam mass flow and accumulative mass release from the accumulator vs.time

3.2 蒸汽喷射过程分析

蒸汽从储汽罐喷射至试验仓的流速可达到超音速.图5给出了0.3s、0.5s、0.7s和1s时刻管道入口至挡板轴线上气体瞬态马赫数分布，图中横坐标位置与图1所示对应.0.3s时阀门部分开启，阀门上游管道内蒸汽流速为亚音速，阀门位置跃升至音速，阀门下游流速继续跃升至超音速，并形成超音速射流.阀门下游管道内和管道出口射流方向蒸汽马赫数呈小幅度波动，这是由于超音速射流经过交替出现的微弱膨胀波和压缩波造成的［7］.射流到达挡板附近马赫数快速减小，流速降至亚音速.0.5s时阀门全开后，在管道入口蒸汽流速跃升至接近音速，在管道内蒸汽流速稍有增大，至管道出口蒸汽流速略高于音速，蒸汽充入试验仓呈欠膨胀超音速射流状态，马赫数大幅度波动，这是由于管道入口产生强烈的膨胀波，膨胀相交并在自由边界反射出压缩波，压缩波相交并汇聚，如此形成节状射流结构［7］.由于挡板距离射流入口较近，射流的第二个波节未能发展完全，流速在挡板附近快速衰减为亚音速，气体沿挡板向仓内流动，见图6所示试验仓入口附近速度云图.0.7s时，蒸汽仍为超音速射流，射流结构与图6所示类似，但马赫数波动幅度显著下降.随着管道入口压力进一步下降以及试验仓内压力升高，蒸汽充入试验仓时的速度波动减弱，1s时蒸汽进入试验仓后不再加速，马赫数先是保持不变之后快速减小.

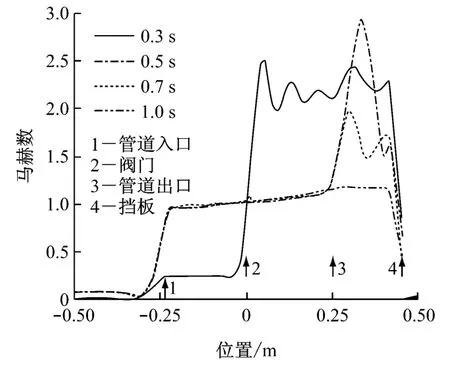
图5 管道入口至挡板轴线气体瞬态马赫数分布Fig.5 Distribution of transient Mach number along pipe axis

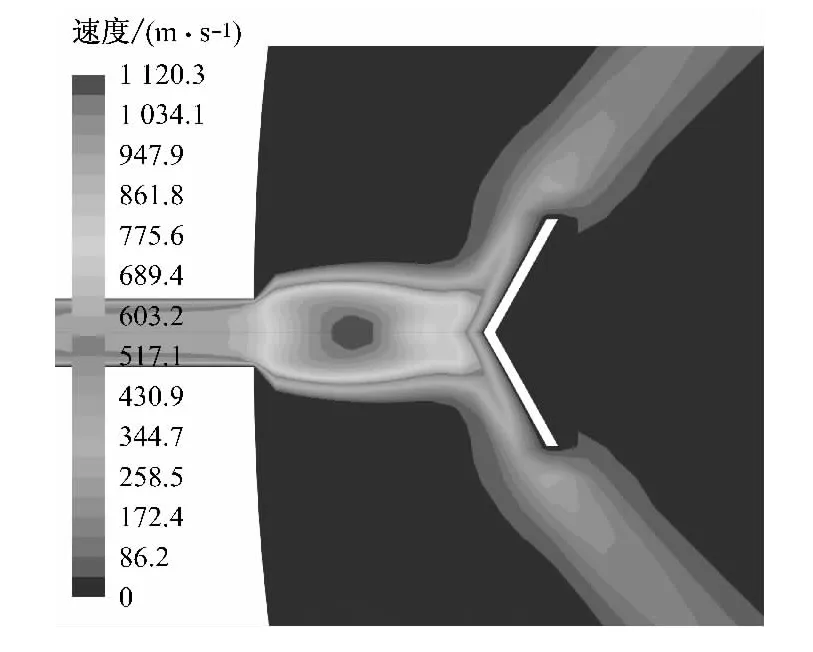
图6 0.5s时试验仓入口附近速度云图Fig.6 Contours of velocity magnitude at inlet of the test chamber at 0.5s

3.3 试验仓气体状态变化

在1s内，超音速蒸汽充入试验仓内，使仓内温度、压力、组分质量分数等状态参数急剧变化.图7给出了试验仓内混合气体温度变化云图，随着蒸汽的不断充入，空气温度升高，并且试验仓内温度分布逐渐趋于均匀.图7（a）中，0.3s时试验仓内大部分区域未发生显著升温，试件周围只有正对入口的端面温度开始接近目标值，仓内温度分布极不均匀；图7（b）中，0.5s时试验仓内大部分区域温度显著升高，试件端面和局部侧面周围的温度达到目标值；图7（c）中，0.7s时试验仓内大部分区域温度达到目标值，且试件周围温度已超过目标值，温度分布已比较均匀，此时的气体流动迹线见图8，气体流动在试验仓内已充分发展；图7（d）中，1s时试验仓内温度进一步升高，温度分布均匀，除入口与挡板附近外，其他区域温差小于10K.数值计算结果表明，H2O质量分数分布与温度分布十分相似，说明物质传输与传热过程同步进行.随着蒸汽的充入，试验仓内的压力不断升高，由于压力传递速度极快，除入口和挡板附近流速变化剧烈造成压力变化较大外，总体上试验仓内压力分布非常均匀.

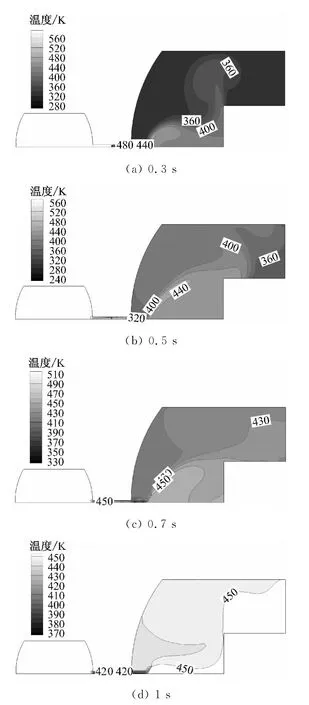
图７ 试验仓内气体温度变化云图Fig.7 Distribution of temperature in the test chamber

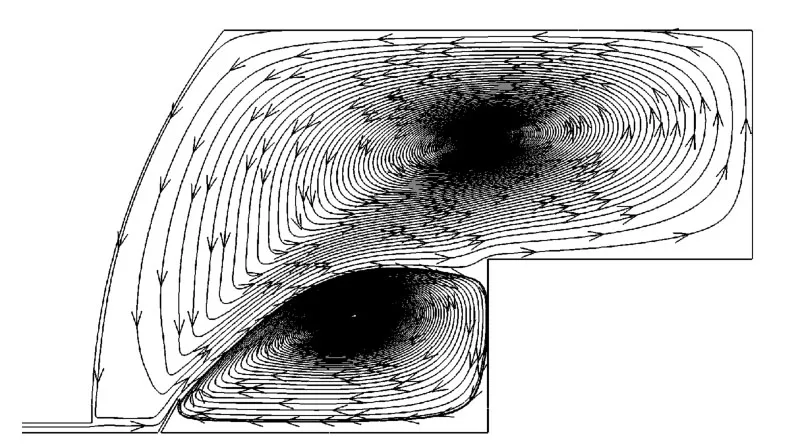
图8 0.7s时试验仓内气体流线图Fig.8 Streamlines of gas in the test chamber at 0.7s

为进一步定量描述试件周围环境状态的变化，图9给出了试件周围监测点（位置示于图1）温度、H2O质量分数和压力随时间变化的曲线.图9（a）中，0.2s之前试件周围温度升高非常缓慢，0.2s以后测点C温度急剧升高；0.48s时测点C的温度达到目标值，0.5s以后测点C温度上升速率趋于平缓；0.22s以后测点B的温度也急剧升高，0.32s时测点B的温度达到目标值，之后温度上升速率趋于平缓；测点D的温度在0.5s前缓慢升高，之后急剧上升，至0.58s时温度达到目标值，0.6s以后温度上升速率趋于平缓；测点E的温度在0.6s前缓慢升高，之后急剧上升，至0.7s时温度达到目标值，之后温度上升速率趋于平缓.由图9（b）可见，上述测点的H2O质量分数变化与温度变化趋势十分相似，特别是温度急剧上升阶段与H2O质量分数由0急剧上升阶段相对应，这是由于高温蒸汽以“浪涌”方式充入试验仓，蒸汽到达时，该点H2O质量分数和温度会同时跃升.上述各个测点压力随时间的变化曲线如图9（c）所示，可见各测点的压力相等.

图9 试件周围监测点温度、H2O质量分数和压力随时间的变化Fig.9 Curves of temperature，pressure，H2O concentration vs.time for monitoring points around the specimen

由图9还可以看出，蒸汽快速充入试验仓的过程中，蒸汽的能量传递给试验仓内的空气，能量传递有2种形式：（1）高温蒸汽与空气混合，这一传热过程非常剧烈，当蒸汽与空气混合后，空气温度迅速升高；（2）蒸汽未到达区域的空气受到压缩，能量通过做功形式传递，由于试验仓压力升高较为缓慢，压缩做功引起的温升速率较小.可以验证，图9（a）所示点I－II连线状态变化服从绝热压缩过程.图10所示为测点E温度（点I－II连线）与对应压力的关系曲线，数值计算结果与绝热过程理论计算（取空气绝热指数κ＝1.4）的2条曲线基本重合，可见试验仓内空气压缩服从绝热过程.由此可见，在蒸汽充入过程早期，未与蒸汽混合的空气状态变化满足绝热压缩过程.但是，单纯依靠绝热压缩来达到目标温度是不现实的，此时空气压力需要达到0.305MPa.因此，试验仓达到目标温度主要是依靠蒸汽与空气的混合.

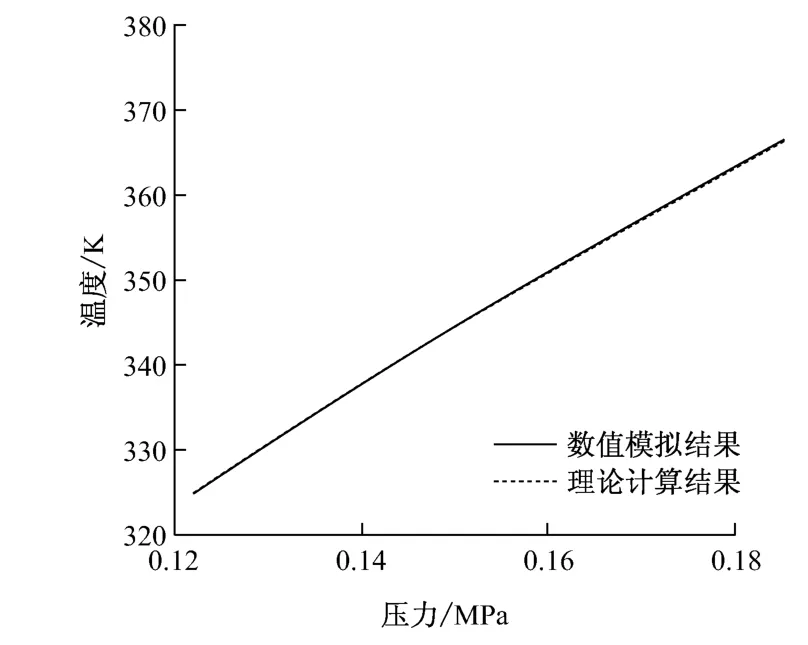
图10 测点E的温度与压力的关系Fig.10 Curve of temperature vs.pressure for monitoring point E

通过上述分析表明，试件周围环境条件在1s内达到DBA试验的目标温度和压力值可以实现.需要注意的是，由于笔者为计算方便选用轴对称模型，蒸汽入射口正对试件两端面，造成试件侧面温度上升有所滞后，实际设计试验时，在试验仓周围合理布置多个蒸汽入射口，可以提高升温的同步性.另一方面，从以上数值模拟结果来看，正对蒸汽入口的试件端面温度可在0.5s内达到目标值，即测温元件至少还有0.5s的响应时间，这对于解决测温元件响应滞后的问题是有利的.虽然，数值模拟结果表明试验仓在1s时的温度和压力已超过目标值，但是在实际的工艺过程中，需要考虑试件和壁面吸热造成的温度和压力的下降，相应的数值模型需要根据实际部件结构和材料进行调整.

4 结 论

（1）采用储汽罐释放高温高压过热蒸汽充入试验仓的方法可以实现DBA试验第1s热冲击要求，试验仓内温度和压力达到目标值，过热蒸汽初始参数可近似通过热力学计算确定.

（2）热冲击过程中试验仓内除蒸汽入口和挡板附近的局部压力分布不均匀外，其他区域压力分布均匀且随时间平稳上升，热冲击过程试验仓内温度分布与蒸汽湍流扩散过程有关，仓内温度阶跃波动上升，温升主要依靠蒸汽与空气的混合，同时空气绝热压缩过程对温升也有贡献，在1s热冲击后期仓内温度分布趋于均匀.

（3）储汽罐蒸汽进入管道后达到音速或超音速，并以超音速射流进入试验仓，在实际设计中，为进一步确保蒸汽瞬时传输至试验仓，可合理增设蒸汽管道，同时也有利于提高试验仓内升温同步性.

［1］Institute of Electrical and Electronics Engineers.IEEE Std 323—2003IEEE standard for qualifying class 1E equipment for nuclear power generating stations［S］.New York，USA：The Institute of Electrical and Electronics Engineers，Inc.，2004.

［2］王琭.LOCA试验质量影响因素分析［J］.中国核电，2008，1（2）：140－145.WANG Lu.Analysis of factors affecting the LOCA test quality［J］.China Nuclear Power，2008，1（2）：140－145.

［3］Association Française pour les règles de Conception，de construction et de surveillance en exploitation des matériels des Chaudières Electro Nucléaires（AFCEN）.NF M 64—001Qualification of electric equipment in a nuclear accident environment［S］.Paris，France：Association Française de Normalisation（AFNOR），1991.

［4］龚国祥，李骥，田金良.核电站LOCA试验装置：中国，CN 202018832U［P］.2011－10－26.

［5］颜昌彪.LOCA鉴定试验台设计研究［J］.广东化工，2011，38（2）：40－42.YAN Changbiao.D＆R of LOCA test bench［J］.Guangdong Chemical Industry，2011，38（2）：40－42.

［6］刘强，帅剑云，黄卫星，等.LOCA炉封闭大空间内承压热冲击过程数值模拟研究［J］.化工装备技术，2009，30（1）：39－43.LIU Qiang，SHUAI Jianyun，HUANG Weixing，et al.Numerical investigation of PTS process in a large enclosure of LOCA furnace［J］.Chemical Equipment Technology，2009，30（1）：39－43.

［7］赵承庆，姜毅.气体射流动力学［M］.北京：北京理工大学出版社，1998：129－143.