病态线性模型参数估计的主元加权迭代法
王永弟,赵好好
(南京信息工程大学 遥感学院,江苏 南京 210044)
一、引 言
病态性问题存在于测量数据处理、地球物理参数反演、回归分析等与参数估计有关的诸多领域,其危害严重性受到相关领域科技工作者的广泛关注。当模型中存在病态性时,参数最小二乘估计的性质会显著地变坏,参数估值的质量难以得到保证。分析模型的病态性质、克服或减弱模型病态性、取得更为准确的参数估值,是当前测量平差中的一个重要问题。
近年来,关于如何解决满秩、秩亏和附有条件的参数平差模型中的病态问题,得到了测绘地理信息界普遍的重视,许多学者[1-8]对此进行了深入而系统的研究,并取得了一系列重要的成果。在诸多克服或减弱模型病态性的方法中,一大类是以岭估计、广义岭估计、主成分估计和Stein压缩估计等为代表的有偏估计,其实质是以牺牲最小二乘估计的无偏性来换取参数估计的稳定性和参数估值的可靠性,具有结果有偏和参数确定困难两个缺点;另一大类是以矩阵的奇异值分解法、遗传算法及误差方程的正交化等为代表,其原理都比较深奥,在实际工作中应用不便。
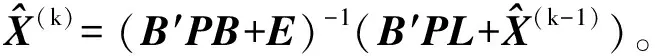
文献[9]中提出一种新的迭代算法——主元加权迭代法,其主要思想是采用主元加权的预处理手段。即首先降低系数矩阵的条件数,随着条件数的降低,其病态性也会随之得以改善和消除;然后组成一个简单的迭代公式进行求解,经过这样的处理以后,数值解的精度能够得到较大幅度的提高。
本文将文献[9]提出的主元加权迭代法引入到测量数据处理中,以观察主元加权迭代是否能够达到与谱修正迭代法相同的效果。分别就良态和病态两种情况选择了两个实际算例,主要对主元加权迭代法和谱修正迭代法两种方法在不同情形下的表现进行了对比和分析。
二、主元加权迭代方法
1. 主元加权迭代法
测量数据处理中存在诸多病态线性方程组,一般为如下形式
Ax=b
(1)
对于病态线性方程组,A和(或)b如果存在一个小的扰动δA和(或)δb,则会对解产生比较大的误差。误差放大的倍数用系数矩阵的条件数cond(A)来衡量,当系数矩阵严重病态时,cond(A)≫1。
若采用主元加权方法,改善病态矩阵条件数,形式如下
A+αE
(2)
式中,A为n阶正定方阵,E为n阶单位矩阵。
关于矩阵A+αE的条件数改善问题,文献[9]给出定义及其证明,在此仅给出定义,证明详见文献[9]。
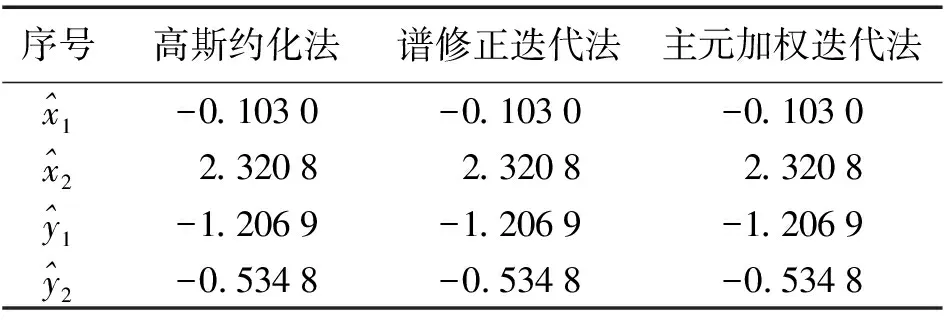
定义:对于正定对称矩阵A,当α>0 时,则cond(A+αE) 权因子α的选取是否得当是主元加权方法是否有效的关键。当α值过小时,对矩阵A的条件数改善效果不明显,则A仍严重病态,此时解的精度仍然很低;当α值过大时,收敛速度则会变慢,甚至解会失真。文献[9]根据文中所处理的系数矩阵,在Matlab中经过多次计算后确定α取值为2时比较合适。 测量数据处理中存在诸多病态线性方程组,一般为如下形式 Ax=b (3) 将式(3)的主元叠加一个权值来改善条件数,则得到与式(3)同解的另一种形式 (A+αE)x=b+αx (4) 由于式(4)两端分别含有解向量x,则可构造迭代公式为 (A+αE)x(k+1)=b+αx(k) (5) 令x(k+1)=x(k)+e(k),则 (A+αE)(x(k)+e(k))=b+αx(k)⟹(A+αE)x(k)+(A+αE)e(k)=b+αx(k)⟹(A+αE)e(k)=b-Ax(k) (6) 针对平差问题中的良态和病态两种情况,下面利用高斯约化法、谱修正迭代法和主元加权迭代法等3种方法,通过实例对良态和病态两种实际平差问题分别进行讨论。 本例取自文献[11]第130页中的例7~9。在该三角网坐标平差中,得到的法方程为 (7) 法方程系数矩阵的条件数为2.714 7,因此该法方程为良态方程。利用高斯约化法、谱修正迭代法和主元加权迭代法3种方法分别进行计算,计算结果见表1。 表1 计算结果 表1中,所有结果在3种方法中完全相同。由以上结果可知,当平差问题中的法方程为良态时,无论是谱修正迭代法还是主元加权迭代法,均能得到与高斯约化法完全一致的计算结果。 本例取自文献[3]。其中的法方程为 (8) 表2中,3种方法的参数估值与模拟真值之差的2-范数分别为:31.826 2(高斯约化法)、0.341 5(谱修正迭代法)和0.000 9(主元加权迭代法)。由以上计算结果可知,当法方程为病态方程时,谱修正迭代法和主元加权迭代法均显著优于高斯约化法,即这两种方法都能很好地改善最小二乘估计,其中主元加权迭代法的改善效果更为明显。 表2 计算结果 在良态法方程平差问题中,使用主元加权迭代法能得到与谱修正迭代法和高斯约化法完全一致的计算结果;在病态法方程平差问题中,主元加权迭代法得到的结果比谱修正迭代法和高斯约化法的结果更加明显地接近真值。因此,从实际应用的角度来讲,主元加权迭代法是一种非常实用的计算方法。因此,当在使用主元加权迭代法来解决一般的平差问题时,无论方程有无病态,均可使用完全相同的测量数据处理程序平差,大大增强了数据处理程序的适用性。但实际工作中参数的真值往往无法获得,计算结果的好坏均是通过参数估值与模拟真值之差的2-范数来比较估值精度的改善程度,因此,是否有更加合理的针对结果改善程度的评估方法,还有待进一步研究。 参考文献: [1] 卢秀山.病态系统分析理论及其在测量中的应用[D].北京:中国科学院,1999. [2] 王新洲.非线性模型参数估计理论与应用[M].武汉:武汉大学出版社,2002. [3] 王新洲,刘丁酉,张前勇,等.谱修正迭代法及其在测量数据处理中的应用[J].黑龙江工程学院学报,2001,15(2):1-6. [4] 王振杰.大地测量中不适定问题的研究[D].北京:中国测绘科学研究院,2003. [5] 吴杰,李明峰,余腾.测量数据处理中病态矩阵和正则化方法[J].大地测量与地球动力学,2010,30(4):102-105,108. [6] 吴杰,苗恒严.测量数据处理中病态矩阵和部分有偏估计方法[J].测绘通报,2010(9):9-11. [7] HOERL A E,KENNARD R W. Ridge Regression: Biased Estimation for Nonorthogonal Problems [J]. Technom etrics,1970,12(1):55-67. [8] 葛旭明,伍吉仓.病态总体最小二乘问题的广义正则化[J].测绘学报,2012,41(3):372-377. [9] 唐丽,李鹏飞.主元加权迭代法求解病态线性方程组[J].科学技术与工程,2012,12(2):381-383. [10] 武汉测绘科技大学测量平差教研室.测量平差基础[M].3版.北京:测绘出版社,1996.2. 主元加权迭代算法计算步骤
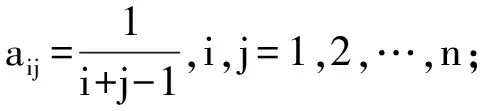
三、实例应用
1. 法方程良态的平差问题
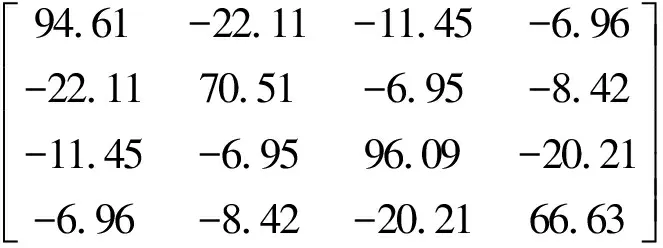
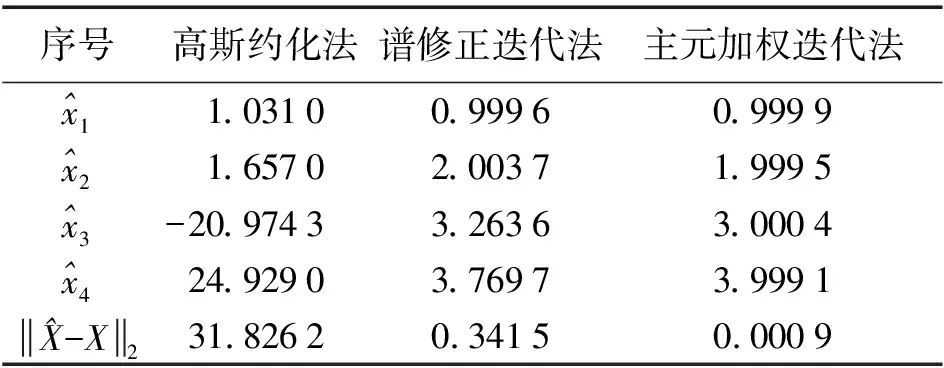
2. 法方程病态的平差问题
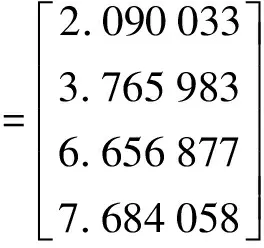
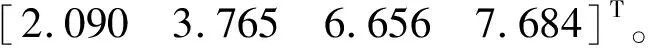
四、结束语

