基于K-means聚类分析的球冠谐函数拟合高程异常方法

孙佳龙，崔旭升，郭淑艳

(淮海工学院 测绘工程学院，江苏 连云港 222001)

一、引 言

高精度的高程异常曲面模型与GPS定位技术相结合可以在一定程度上取代传统繁琐的几何水准测量方法，可大幅度提高测绘工作效率[1-3]。而对高程异常曲面拟合时，目前常用的拟合方法主要有多项式拟合法、移动二次曲面拟合法和多面函数拟合法等[4-7]。在拟合区域较小的情况下，一般的拟合方法可以达到较高的精度，但由于这些方法未顾及似大地水准面的物理性质，拟合出的曲面只能是高程异常的趋势面，与高程异常的实际数值存在一定差异[8]。球冠谐分析作为一种谱方法，由非整阶勒让德函数和三角函数张成的近似空间具有良好的逼近性质，可以实现与高程异常曲面的最大逼近[8-9]。而在利用球冠谐函数拟合高程异常曲面时，选择不同的拟合点，对最后的拟合结果有较大的影响。由于其选择方法目前尚无可靠的理论依据，为此本文提出了基于K-means聚类的球冠谐函数拟合法，即以K-means聚类方法对拟合点进行有效选取，利用选择的拟合点建立球冠谐函数模型，依此模型解算检核点处的高程异常值，从而对拟合精度进行评价。

二、球冠谐函数模型

球冠谐函数是球冠坐标系下满足位理论边界条件的谱函数，它是局部区域对应的特征函数。在球坐标系下对Laplace方程进行求解，得到球谐函数逼近模型[3]

(1)

球冠谐函数与球谐函数的区别在于用非整阶勒让德函数代替整阶勒让德函数，余纬θ的定义域由[0,π]变为[0,θ0]。为了计算方便，需要把通过地球北极的坐标轴Z轴沿子午线旋转到通过球冠的中心，使经度λ仍然满足周期性的边界条件[8]。非整阶勒让德函数序列是由球冠的大小来确定的，对于半角不同的球冠，非整阶勒让德函数序列是不同的，且非整阶勒让德函数由以下边界条件确定

(2)

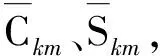
三、基于K-means聚类的球冠谐函数拟合方法

当用球冠谐函数表示残差高程异常时，由于选择的拟合点对高程异常曲面拟合有较大影响，因此，需要对所有的高程异常值进行选取。人为选取高程异常值既耗时又费力，且容易出错。因此，合理有效地选取高程异常值，使这些高程异常能很好地表示该区域的高程异常变化就显得尤为必要。聚类分析是对样本进行分类的一种多元统计方法，是从样本中发现有用信息的一种有效手段[10-11]。聚类是基于“物以聚类”的朴素思想，将数据对象分组成为若干个类或簇，使得在同一个簇中的对象之间具有较高的相似度，而不同簇中的对象差别很大。K-means聚类算法是由MacQueen提出的，该算法是一种在科学研究中被广泛应用的一种经典聚类算法[11]。本文以K-means算法为聚类分析的分类方法，以欧氏距离作为相似性统计量，对高程异常数据进行了聚类分析。考虑到高程异常曲面不仅与样本点的地理位置有关，还与该点的高程异常值的大小有关，因此，本文以三维欧氏距离作为相似性统计量[10]，即

(3)

式中，(xi,yi)、ξi分别为Pi点的坐标和高程异常，d为距离。由于高程异常的单位与坐标单位不同，在进行聚类分析之前需将高程异常数据进行规格化处理[10]

(4)

式中，i=1,2,3；P为规格化处理后的高程异常所对应的坐标和高程异常值。

四、实例解算与分析

某地区D级GPS控制网布设了17个观测点，对其进行了GPS观测和三等水准测量，利用GPS获得的大地高和水准测量得到的正常高，得到17个GPS/水准点的高程异常。从17个高程异常点中选择12点参与球冠谐函数拟合，另外5个点对拟合精度进行检核。因此，需要对17个数据进行聚类分析，从每个聚类中选取欧氏距离最长的点作为高程异常曲面拟合点，构建球冠谐函数模型，其中球冠极点选在区域中心，而球冠半角为1°，全部观测点均落入定义的球冠内。以另外5个点的数据作为外部检核，外符合精度为

(5)

式中，νi为检核点实测高程异常与拟合高程异常的差值；m为检核点个数。检核结果见表1。

表1 基于K-means聚类的球冠谐函数拟合的外部检核结果 mm

从表1中可以看出，随着分类数从2开始，球冠谐函数拟合的精度有所提高，当分类数为5时，精度最高，达到5.5 mm；随着分类数继续增加，精度又开始下降，当分类数为12时，精度最低，为145.8 mm。由此说明，通过对样本数据进行有效分类，可以有效地提高球冠谐函数的拟合精度。为了综合评价基于K-means聚类分析的球冠谐函数的拟合精度，本文还利用同样的数据，从17个点中随机选取12个点，以多项式曲面、移动曲面、多面函数和球冠谐函数这4种常用的曲面拟合模型作为参考模型，比较各种模型之间的拟合精度，结果见表2。

表2 拟合结果残差比较 mm

从表2中可以看出，移动二次曲面拟合的结果中，残差最大值为150 mm，为各种拟合函数中的最大值，其标准差和外符合精度也都最大，说明移动二次曲面拟合的精度在4种方法中最差。5种评价指标都显示，基于K-means聚类分析的球冠谐函数拟合的精度是最优的，其外符合精度最高，达到5.5 mm。各个检核点的高程异常残差值如图1所示。

图1 5种拟合方法得到的高程异常残差值

从图1中可以看出，移动二次曲面在5个检核点的高程异常残差值波动较大，说明该函数模型未能很好地表示该区域的高程异常变化趋势；两种球冠谐函数得到的高程异常残差变化幅度都很小，说明球冠谐函数能很好地逼近高程异常曲面，因此拟合精度较高。而基于K-means聚类分析的球冠谐函数在检核点处的高程异常残差变化比球冠谐函数更平缓、幅度更小，说明K-means聚类方法能对高程异常点进行有效分类，从而能从数量较多的已知高程异常数据中选择有代表性的特征点，再结合球冠谐函数的逼近性质，提高了高程异常曲面的拟合精度，因此拟合精度更高。

五、结束语

基于K-means聚类分析的球冠谐函数拟合法，将差异较小的数据归入同类，在同一聚类中选择欧氏距离最长的点作为高程异常曲面拟合点，利用球冠谐函数很好的逼近性质，实现了高程异常曲面的有效逼近。实例分析结果表明，基于K-means聚类分析的球冠谐函数拟合方法比多项式曲面拟合、移动曲面拟合、多面函数和球冠谐函数的拟合精度更高，因此，利用该方法可以在一定程度上提升高程异常曲面拟合精度。

参考文献：

[1] 李斐, 岳建利, 张利明. 应用GPS重力数据确定(似)大地水准面[J]. 地球物理学报, 2005, 48(2): 294-298.

[2] 郭东美, 许厚泽. 应用GPS水准与重力数据联合解算大地水准面[J]. 武汉大学学报：信息科学版, 2011, 36(5): 621-624.

[3] 程芦颖, 许厚泽, 顾及测站点上重力场信息的大地水准面高的拟合方法[J]. 武汉大学学报：信息科学版, 2008, 33(7): 701-705.

[4] 马洪滨, 董仲宇. 多面函数GPS水准高程拟合中光滑因子求定方法[J]. 东北大学学报：自然科学版, 2008, 29(8): 1176-1178.

[5] 王殊伟, 李斐, 柯宝贵,等. 基于BP神经网络算法的GPS水准高程转换[J]. 武汉大学学报：信息科学版, 2009, 34(10): 1190-1194.

[6] 张勤, 赵超英. 地壳垂直形变场逼近的球冠谐分析法[J]. 测绘学报, 2004, 33(1): 39-42.

[7] 彭富清, 于锦海. 球冠谐分析中非整阶Legendre函数的性质及其计算[J]. 测绘学报，2000, 29(3): 204-208.

[8] 胡伍生, 华锡生, 张志伟. 平坦地区转换GPS高程的混合转换方法[J]. 测绘学报, 2002, 31(2): 128-133.

[9] 冯林刚, 郅军义, 宝因乌力吉. 应用EGM2008模型和GPS/水准数据确定局部似大地水准面[J]. 测绘通报, 2011(1): 18-20.

[10] 杨圣云, 袁德辉, 赖国明. 一种新的聚类初始化方法[J]. 计算机应用与软件, 2007, 8(24): 51-52.

[11] 毛韶阳, 林肯立. 优化k-means初始聚类中心研究[J]. 计算机工程与应用, 2007, 43(22): 179-181.