多针状氧化锌晶须的等效电磁建模及仿真*
赵雨辰,万国宾
(西北工业大学 电子信息学院,西安 710129)
四针状氧化锌晶须(T-ZnOw)是最早由日本松下产业株式会社于1989年研制成功的,其形状与过去的晶须完全不同,为立体四针状单晶体,其多方面的功能已引起材料界的高度重视[1].经过多年的发展,目前ZnOw主要有纤维状、多针状这两大类.纤维状ZnOw也称为一维纳米ZnOw材料,近十几年来,研究人员利用各种方法陆续合成了多种一维纳米ZnOw材料[2].而作为多针状氧化锌晶须(M-ZnOw)的典型代表,T-ZnOw由于其独特的空间三维立体构型和良好的单晶性,不仅拥有其他材料难以比拟的丰富多样的优秀性能,同时由它组成的复合材料呈各向同性,性能远优于由单一纤维状晶须组成的复合材料,具有增强耐磨、防滑、降噪及吸波等优良的综合性能,是目前氧化锌晶须研究的热点[3].M-ZnOw是在 T-ZnOw基础上发展起来的具有更复杂三维形状的氧化锌晶须.研究人员由乙二胺辅助的水热过程中制备出了形态更为复杂的氧化锌晶须,并系统地研究了其生长机理,形态调制和微波吸收性能,结果显示相比于单针状的ZnOw,多针状ZnOw吸波性能要更为优异[4].
具体到吸波材料领域,由于具有高介电损耗、低电阻率、抗菌、高强高模和耐高温等特性,ZnOw是一种理想的功能材料和结构材料,因此许多研究人员都通过实验的方式,对不同条件下不同形态ZnOw,特别是T-ZnOw的微波吸收性能,微波-热转换特性等性能进行了研究[5-7].目前对于ZnOw的吸波特性实验研究较多,而理论建模研究较少,直到2010年Fang等人从微观结构的电磁响应出发,推导了T-ZnOw对于入射电磁波吸收的表达式,才对T-ZnOw的微波能量衰减的定量分析进行了较为详细的阐述[8].而由于ZnOw可以通过物理化学的方法制备成多种形态的晶须,而不仅仅限于四针状,因此对于M-ZnOw吸波特性的理论建模还有待进一步的完善.
文中采用等效电磁参数的研究思路,即采用宏观电磁响应的一致性近似而非具体微观结构电磁响应的理论推导的方式,对M-ZnOw复合材料的等效电磁参数提取理论进行了研究.对不同形状填充粒子的宏观电磁响应进行建模和分析,通过引入等效球形粒子得到了M-ZnOw的等效电磁参数的上下界闭式表达式,通过与实验数据的对比验证了所建立的表达式的有效性,并讨论了涂覆层参数的影响.
1 复合材料仿真建模与分析
1.1 复合材料仿真模型的建立
文献[8]中T-ZnOw复合材料可以被认为是包含一个四针状晶须的立方体单胞按周期排列所组成的周期结构,因此这里采用Ansoft公司的高频电磁仿真软件 (High Frequency Structure Simulator,HFSS)对不同形状粒子填充的复合材料建立其周期结构模型,包括球形粒子、多针状粒子以及条形粒子,如图1所示.在建立模型时,将不同形状填充粒子的体积设置为相同的,即复合材料各组分材料的占空比不变,并将基体材料的介电常数设为2,磁导率设为1.
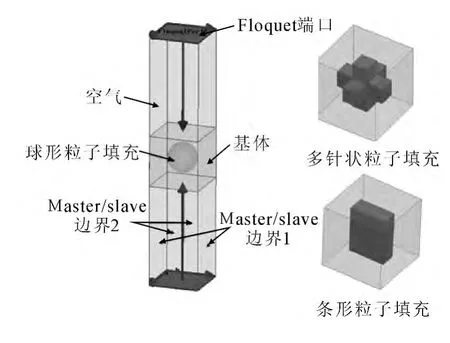
图1 复合材料仿真模型Fig.1 Simulation model of composite
1.2 宏观电磁响应的对比和分析
由于填充粒子的特性,包括材料、形状等是影响复合材料的宏观电磁响应的重要因素,因此这里对不同特性的三种形状粒子填充的复合材料的宏观电磁响应S11进行了对比.
图2是强散射粒子填充的情况,三种不同形状粒子材料均设为理想电导体(Perfect Electronic Conductor,PEC).入射电场方向由Floquet端口的模式所确定,图2(a)和图2(b)分别对入射电场极化方向为x方向和y方向时的S11进行对比,其中re表示实部,imag表示虚部.从图2可知,当入射电场极化方向为x方向时,三种不同形状粒子填充的复合材料其S11曲线各不相同,说明此时三种复合材料对于入射电磁波的宏观响应各不相同.由于各组分材料的本征电磁参数和占空比并未改变,所以粒子形状的影响是造成宏观电磁响应不同的主要原因.当入射电场极化方向为y方向时,一方面对于球形和多针形粒子填充的复合材料,S11曲线与x方向极化时并无明显差别,说明所填充的粒子对这两个方向的极化的电磁波而言具有各向同性性质,或者更准确地来说,在所建立的模型中,多针状粒子具有准各向同性性质;另一方面条形粒子填充时的S11曲线发生了较明显的变化,从数值上来看更接近于多针形粒子填充时的结果,这是因为在y方向两者形状上更为接近.
图3是有损耗粒子填充的情况,三种不同形状粒子材料均设为FR4,其介电常数为4.4(1-j0.02).从图中可以看出,当填充的粒子具有一定的损耗时,不论入射电场极化方向是x方向还是y方向,三种不同形状粒子填充的复合材料其S11曲线基本相同,但相对于y方向极化的入射波,条形粒子对x方向极化的入射波的宏观响应与其它两种粒子有一定差距.这是由于当填充粒子不再具有强散射特性,而是具有一定的电损耗时,其对于入射电磁波具有一定的衰减作用,此时由其组成的复合材料中粒子与粒子之间的相互作用将会比填充强散射粒子时小很多,于是在各组分材料的本征电磁参数和占空比并未改变的情况下,复合材料的宏观电磁响应受到粒子形状的影响并不大.通过以上分析发现,填充粒子具有一定的损耗 时,球形粒子和多针状粒子填充的复合材料具有基本一致的宏观电磁响应,而实际中的M-ZnOw本身就具有一定的电磁波吸收能力,因此在建立其等效电磁参数的闭式表达式时,可以采用等效的球形粒子来简化其特殊的三维结构.
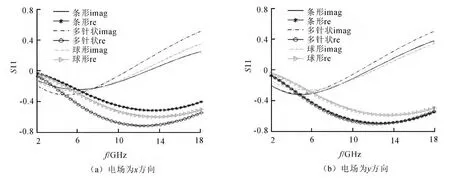
图2 PEC粒子填充的情况Fig.2 Filled with PEC particle

图3 有损耗粒子填充的情况Fig.3 Filled with lossy particle
2 M-ZnOw的等效电磁参数提取理论
2.1 等效球形粒子半径
引入的等效球形粒子与M-ZnOw具有相同体积,因此不会改变填充颗粒的体积分数.定义l和d分别表示M-ZnOw每根针的长度和根部的半径,Num表示针的数目,而M-ZnOw核心部分可以看成是一个直径为D的球形,因此等效球形粒子的半径可以表示为

对于T-ZnOw,Num =4.
2.2 HS变分理论
假设复合材料是由N种均匀粒子组成的,并且粒子都具有各态遍历特性,记复合材料中各种粒子的占空比分别为f(p)(p=1,2,…,N),根据 HS变分理论,对于具有各态遍历性的复合材料,可选取一参考媒质,其介电常数可以取为基体材料的介电常数,即ε(0)=ε(1),这里记基体材料的介电常数为ε(1).于是,根据HS变分理论复合材料等效介电常数张量的表达式为

S表示几何因子.从ε(0)≤min{ε(p)}时式(2)给出了等效介电常数的下界表达式,当时ε(0)≥max{ε(p)},则给出上界表达式
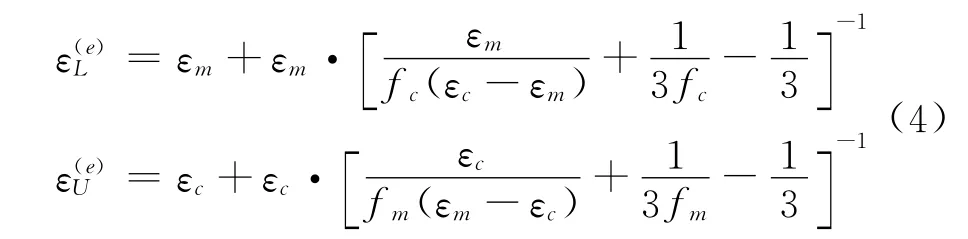
其中fm和fc分别表示基体和填充粒子的占空比,εm和εc分别是基体和等效球形粒子的介电常数,下标U和L分别表示上界和下界.由于是球形粒子,推导时S取1/3.等效磁导率的计算公式和等效介电常数相同.
2.3 核壳粒子理论
虽然T-ZnOw有许多优点,但其吸波性能仍然具有一定的局限性,通过在T-ZnOw表面采用物理化学的方法涂覆一层具有磁损耗的材料,可以提高其吸波性能,并且已经有了用Fe包覆TZnOw的相关实验研究[7].从等效球形粒子的角度看,包覆了Fe的T-ZnOw可以等效为具有核壳结构的球形粒子,定义t表示涂覆Fe的厚度,核的半径记为R1,可由式(1)求得,则壳的半径为R2=R1+t,若记ε1为核的介电常数,ε2为壳的介电常数.于是可得核壳粒子的等效介电常数εc为

3 理论的验证与分析
3.1 等效理论的验证
为了验证所建立的等效电磁参数预测公式,将计算结果与文献中已有的实验结果进行对比.文献[7]中通过实验的手段测量了涂覆Fe的T-ZnOw与石蜡复合材料等效磁导率,其中填充的TZnOw/Fe粒子的占空比为0.75.根据式(4)采用等效球形粒子的近似方法计算了T-ZnOw/Fe复合材料的等效磁导率.Fe的本征磁导率取自文献[9],而T-ZnOw和石蜡的磁导率均取1,T-ZnOw/Fe粒子的几何参量l,d,t和D 分别取5,1,100 μm和1.2μm,计算结果与实验结果的对比如图4所示.

图4 与实验结果的对比Fig.4 Comparison with experimental results
从图中可以看出理论计算结果与实验结果吻合较为良好,其中等效磁导率实部在2GHz和18 GHz附近与实验结果较为接近,在10GHz左右与实验结果具有一定的差距,数值上大约比实验结果小0.3左右,而等效磁导率虚部的吻合程度要比等效磁导率实部好.
3.2 涂覆层参数的影响分析
由于T-ZnOw和石蜡的磁导率均为1,所以复合材料的磁导率主要取决于涂覆Fe的厚度和参数.因此在验证了理论预测公式的准确性后,进一步分析了不同情况下涂覆层,即壳的参数的影响.在图5中,对涂覆Fe的厚度分别为100nm和400 nm时的理论预测值进行了分析,计算时各组分的磁导率取2GHz时的值.从图中可以看出,当Fe的厚度较薄时,上下界计算的结果比较接近,而当Fe的厚度增加时,下上界之间的差距就随之增大,这是由于在计算时T-ZnOw和石蜡的磁导率均为1,所以在Fe含量较小时,上下界的差别也很小.
图6在填充粒子的占空比分别为0.15,0.35,0.55和0.75的情况下,研究了壳的磁导率对最终计算的等效磁导率的影响.从图中可以看出,等效磁导率随着壳的磁导率的增加而快速增加,但当壳的磁导率进一步增加时,上界表达式所预测的等效磁导率的增加幅度不变,而下界的开始放缓,并且当填充粒子的占空比越小时,其对应曲线的斜率也越小.
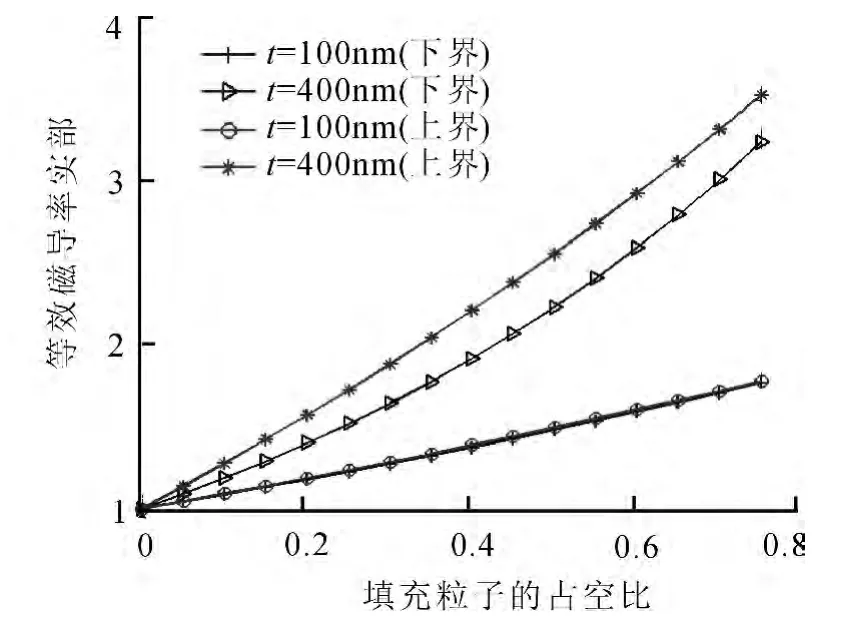
图5 涂覆层厚度的影响Fig.5 Influence of coating thickness
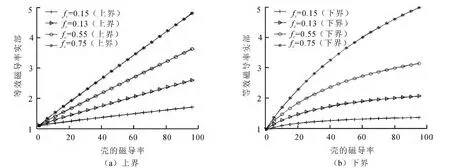
图6 涂覆层渗透性的影响Fig.6 Influence of permeability of coating layer
4 结论
1)对于填充不同粒子的复合材料,填充粒子的散射特性和形状都会对其宏观电磁响应产生影响,当粒子具有一定的损耗时,具有准各向同性性质的粒子和标准的球形粒子具有相近的宏观电磁响应.
2)由于具有相似的宏观电磁响应,以T-ZnOw为代表的具有准各向同性性质的M-ZnOw粒子可以通过一个等效的球形粒子来表示,简化了其几何结构的复杂性.
3)在使用等效球形粒子简化T-ZnOw的基础上,采用核壳粒子等效理论和HS变分理论可以较为准确地预测T-ZnOw/Fe复合材料的等效电磁参数,与实验结果相比,在2~18GHz频段内,对复合材料的磁导率实部预测值误差小于0.3,虚部预测值误差小于0.1.
[1]ZENG A,ZHENG Y,GUO Y,et al.Effect of Tetra-Needle-Shaped Zinc Oxide Whisker(T-ZnOw)on Mechanical Properties and Crystallization Behavior of Isotactic Polypropylene[J].Materials & Design,2012,34:691.
[2]张雪川,张跃,袁洪涛,等.MOCVD法制备一维定向ZnO晶须阵列及掺杂研究[J].人工晶体学报,2005,34(6):972.ZHANG Xue-chuan,ZHANG Yue,YUAN Hongtao,et al.Study on One-dimension Well-Aligned ZnO Whiskers and Doping by MOCVD[J].Journal of Synthetic Crystals,2005,34(6):972.(in Chinese)
[3]郭岚,傅敏恭,万益群,等.四针状氧化锌晶须的制备及其吸波性能的研究[J]无机化学学报,2007,23(7):1251.GUO Lan,FU Min-gong,WAN Yi-qun,et al.Tetrapod-shaped ZnO Whiskers:Preparation and Microwave Absorption Behaviors [J]. Chinese Journal of Inorganic Chemistry,2007,23(7):1251.(in Chinese)
[4]HU Q,TONG G X,WU W H,et al.Selective Preparation and Enhanced Microwave Electromagnetic Characteristics of Polymorphous ZnO Architectures Made from a Facile One-Step Ethanediamine-Assisted Hydrothermal Approach[J].CrystengComm,2013,15(7):1314.
[5]YUAN F Y,ZHANG H B,LI X F,et al.Synergistic Effect of Boron Nitride Flakes and Tetrapod-Shaped ZnO Whiskers on the Thermal Conductivity of Electrically Insulating Phenol Formaldehyde Composites[J].Composites Part A:Applied Science and Manufacturing,2013,53:137.
[6]KONG L,YIN X W,YE F,et al.Electromagnetic Wave Absorption Properties of ZnO-Based Materials Modified with ZnAl2O4Nanograins[J].The Journal of Physical Chemistry C,2013,117(5):2135.
[7]夏宁博,刑欣,司亚凯,等.四针状氧化锌晶须吸波性能的改进[J].安全与电磁兼容,2009,21(1):57.XIA Ning -bo,XING Xin,SI Ya -kai,et al.Improvement on Microwave Absorption Property of Tetrapod-Shaped ZnO Whiskers[J].SAFETY &EMC,2009,21(1):57.(in Chinese)
[8]FANG X Y,CAO M S,SHI X L,et al.Microwave Responses and General Model of Nanoteraneedle ZnO: Integration of Interface Scattering,Microcurrent,Dielectric Relaxation and Microantenna[J].Journal of Applied Physic,2010,107:054034.
[9]彭伟才,陈康华.磁性纤维随机混合媒质等效电磁参数的计算[J].稀有金属材料与工程,2005,34(9):1407.PENG Wei-cai,CHEN Kang-hua.Calculation of Effective Electromagnetic Parameters in Random Mixture Media of Magnetic Iron Fiber[J].Rare Metal Materials and Engineering,2005,34(9):1407.(in Chinese)

