数学教学中学生直觉思维发展的“形象转化”策略

王志南

一、沟通新旧情境，在形象转化中唤醒直觉之眼

直觉思维的触发与思维者的认知储备、思维经验有着密切的联系。因此，在展开直觉思维的过程中，教师要善于通过形象转化沟通新旧问题情境，链接学生已有认知储备和思维经验，进而唤醒学生的直觉之眼。

如苏教版六年级下册课本中有这样一道思考题：一个圆锥和一个圆柱的底面积相等，体积的比是1：6。如果圆锥的高是4.2厘米，圆柱的高是多少厘米？如果圆柱的高是4.2厘米，圆锥的高是多少厘米？

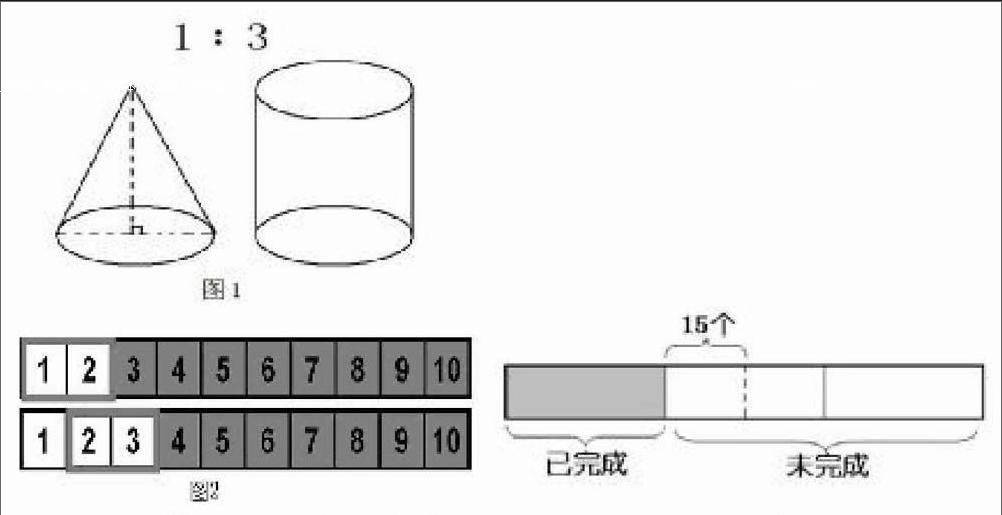
由于问题情境中的已知条件太少，学生普遍感觉解决有困难。那么，如何挖掘学生已有的认知积淀和思维经验呢？显然，仅仅凭借语言的描述对学生来说仍是有困难的，这时就必须借助直观形象的转化，来唤醒学生的直觉思维。教师出示图1，勾起学生对等底等高的圆锥和圆柱体积关系的回忆，进而引发学生的直觉思维，在底面积相等的情况下，要使这里圆锥和圆柱的体积之比为1：6，右边应该有两个这样的圆柱，所以圆柱的高应该是圆锥的2倍。

二、感悟操作活动，在形象转化中启发直觉之思

直觉表现为思维者能快速地掌握问题情境的意义和结构，并对如何解决问题作出猜想和预测。动手操作、自主探究是学生数学学习的重要方式，有助于学生理解抽象的问题情境，易于学生对问题进行直觉的猜想和预测，在形象转化中启发学生的直觉之思。

例如，教学图形覆盖规律时，例题的图表中一共10个数，用方框每次圈两个数，一共可以得到多少个不同的和？在教学时，我让学生首先试着移一移，引导学生体会到每向右移动一次，方框就向右移动一格。（如图2）学生感悟到这一点后，我引导学生大胆地进行猜想，用方框每次圈两个数然后平移，会平移几次？借助已有的感悟和操作活动，学生凭直觉发现：方框每次圈2个数，后面还有8格的位置，平移一次移一格，8格就要平移8次。这样，在不断地大胆猜想、谨慎验证中，不断发展学生数学直觉能力。

三、注重数形结合，在形象转化中感受直觉之妙

研究表明，直觉思维有一重要特征——视觉化，即思维者在视觉化中觉察事物。而这种视觉化的思维方式，能使人迅速而整体地把握问题情境，进而帮助理解。因此，将语义表达的数学情境进行数形结合，实现从语义到图象（或表象）的转化，引导学生依托图象展开思考，有助于学生直觉思维的发展。

如在六年级上册的一节复习课上，我给学生出示了这样一道题：加工一批零件，第一天完成的个数与未完成的个数比是1：2，如果再加工15个零件就完成总个数的一半。这批零件一共有多少个？对于刚学分数应用题的学生而言，解决这道题的难点在于难以找到“再加工的15个零件”对应总量的分率。对此，我提示学生，如果用一个长方形表示一共的任务，我们能不能把题目中的条件在图中表示出来呢？

学生通过尝试，画出示意图。（如下图）

通过画图，学生可以凭借直觉思维发现15个零件是6份中的一份，直接用15×6=90个就解决问题了。

当然，在运用直觉思维解决问题之后，引导学生用理性思维分析为什么15×6=90是合理的仍然很重要，进而发现15个对应单位“1”的分率是1/2-1/3=1/6，沟通直觉思维与分析思维的联系。

总之，作为数学教师，要发展学生的直觉思维，还需要有一种深入教学研究的精神，不断思考：哪些数学题材可以发展学生的直觉思维，怎样的学习方式可以促进学生直觉思维的发展，进而探寻发展和培养儿童直觉思维的最佳路径。■

注：本文为江苏省南通市通州区“十二五”教育科学规划课题“基于儿童直觉思维发展的小学数学课堂实践研究”研究成果。

（作者单位：江苏南通市通州区西亭小学）endprint