基于记忆学习法的放疗中呼吸运动预测技术的研究
万伟权 张慧连 徐子海 贺志强 陈超敏*
1(南方医科大学生物医学工程学院, 广州 510515)2(广东新华软件外包有限公司, 广州 510515)3(解放军303医院放射治疗中心, 南宁 530021)
基于记忆学习法的放疗中呼吸运动预测技术的研究
万伟权1张慧连2徐子海3贺志强1陈超敏1*
1(南方医科大学生物医学工程学院, 广州 510515)2(广东新华软件外包有限公司, 广州 510515)3(解放军303医院放射治疗中心, 南宁 530021)
对胸腹部肿瘤进行实时跟踪放疗时,需要通过预测来补偿系统延迟。然而,由于呼吸运动的复杂性,传统方法难以满足要求。本文应用一种基于记忆学习法进行呼吸预测,该方法首先存储训练数据到记忆中,然后查找相关数据应答当前查询。在此基础上,采用“滑窗法”动态更新训练数据集,并针对预测过程中出现的 “病态矩阵”采用脊回归进一步改进算法,使算法的精确性和鲁棒性有了很大提高。实验使用POLARIS红外定位系统采集了10例正常人体表的红外反射标记物的呼吸运动数据样本,平均幅度约为20 mm(9.2~37.8 mm),采用改进后的基于记忆学习法(预测步长为1 s),平均绝对误差约为0.3 mm(0.08~0.8 mm),每次估值耗时约1 ms。所提出的方法能够准确和实时捕捉复杂的呼吸运动轨迹。
放射治疗;记忆学习法;呼吸运动;实时;预测
引言
精确放射治疗技术基本要求是在肿瘤治疗上实现高精度、高剂量、高疗效和低损伤(三高一低),调强放疗技术可产生高度适合三维静态靶区形状的剂量分布。然而由呼吸引起的胸腹部肿瘤运动会使目标肿瘤移出而正常组织进入计划靶区,从而极大影响放疗的效果,并且会增加发生正常组织并发症的概率。为了减小呼吸运动的影响,在传统的放射治疗和IMRT中通常采用肿瘤靶区射野扩边、呼吸限制和呼吸门控等技术。但是,这些技术存在明显的不足之处,并不能达到很好的预期效果。目前,利用图像引导实时跟踪法可以很大程度上减少呼吸运动影响,但从肿瘤信息的获取到射野调整之间存在一般为几百毫秒的系统延迟[1]。为补偿系统延迟,最好的办法是通过数学建模预测肿瘤运动位置[2]。由于外部呼吸信号和胸腹部肿瘤运动具有很好的相关性[3],所以利用呼吸信号控制动态放疗过程成为肿瘤实时跟踪治疗的一个重要研究方向。
Krauss比较了目前4种热门的预测呼吸运动方法:线性回归法、神经网络法、核密度估计法和支持向量回归法,研究发现使用任何一种方法,其均方根误差都比无预测的情况要小[4]。但是,线性回归法不易选择最优历史状态数,准确性较差,且只适用于延时很小的系统;神经网络法受网络结构和样本复杂性的影响较大,容易发生过学习或低泛化能力;核密度估计法计算量很大,难以满足实时性要求;支持向量回归法对大规模训练样本难以实施。本研究提出一种基于记忆学习法[5]预测呼吸运动。该方法首先存储训练数据到记忆中,然后从中查找相似数据回答当前查询。相似性越高的数据点其权值越高。通过相对简单的模型拟合局部区域而不是全局模型,该方法能够正确捕捉极其复杂的非线性关系。由于加权函数的局部特性,该方法对训练数据的异常值有着一定的鲁棒性。而且,训练和适应新数据几乎都是即时完成的。
1 材料和方法
1.1材料
实验使用加拿大NDI生产的POLARIS红外定位系统,采集了10组正常人体表的红外反射标记物的呼吸运动数据。受试者采用仰卧位,标记物置于受试者胸骨剑突下约5 cm处,采样频率设为30 Hz。由于在采集过程中存在一定的噪声,实验对系统采集的原始数据进行平滑滤波,从而得到10例样本。表1是10例样本在头脚方向的呼吸运动幅度。图1是其中两例典型的呼吸运动轨迹:(a)样本1:周期、幅度比较规则的信号 (b)样本9:基线漂移、不等幅变化的不规则信号。算法执行平台是Matlab7.9.0。

表1 各样本的呼吸运动幅度
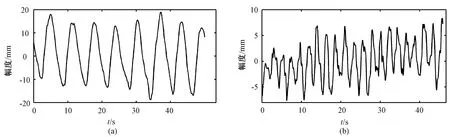
图1 两例典型的呼吸运动轨迹。(a)较规则的信号;(b)不规则的信号Fig.1 Two typical respiratory movement. (a)Regular breathing;(b)Irregular breathing
1.2基于记忆学习法原理
以采样频率φ=30 Hz进行数据采集,得到一组历史呼吸轨迹对应的离散样本{s1,s2,si…sM},当i≤M-L时,构建状态向量:xi={si-Dτ,si-(D-1)τ…si}T,其中si表示i时刻测量点的运动幅度,D(≥2)是输入向量维数,τ是元素间隔长度,L是预测的步长。yi表示i+L时刻测量点的运动幅度。训练集即表示为S={(xi,yi)}。
基于记忆学习法(memory-based learning,MBL)直到需要应答某查询时才处理训练数据。它包括存储训练数据到记忆中,以及查找相似数据回答特定查询。相似性通常利用距离加权函数来判断,相似性越高的点其权值越高。最简单的是最近邻法,选择最近点的输出值,但通常会造成输入和输出之间不连续函数映射,给出不理想的结果。本文使用高斯核
(1)

(2)
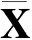
(3)

(4)
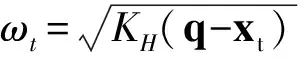
1.3算法改进
1.3.1动态更新训练集
上述的基于记忆学习法的训练集是静态不变的,预测准确性随着训练集的增大而提高。然而训练集太大会导致搜索速度过慢。另外,呼吸运动随着时间变化而不规则变化,查询点与训练集相隔时间越长,其相似程度越低。因此,先采集一段数据构成初始训练集,随着测量的进行,采用“滑窗法”持续进行更新,使得训练集始终包含最新数据[6]。
1.3.2脊回归[7]
采用动态更新训练集方法后,对应不同训练集长度,预测准确性都有了很大的提高。当训练集大小为5 s(一个典型的呼吸周期结束的最小持续时间)时,绝大部分数据拟合程度最好,但某些时刻会出现偏差非常大的情况。分析原因,是因为过拟合而使信息矩阵XTWTWX奇异或接近奇异成为“病态”[8],造成其逆矩阵的极度膨胀,进而大大增加回归系数的误差均方,影响回归拟合的准确性和稳健性。本研究尝试使用脊回归进行结果优化。
为简单描述,令X=WX,Y=WY,b=(XTX)-1XTY=(b0,b1…bD+1)T,引入一个非负因子σ,则b(σ)=(XTX+σθI)-1XTY,I为单位矩阵,θ为奇异临界值。这样det(b(σ))的值就能迅速变大,从而改进估计值质量。脊回归分析通常要先对X变数做中心化和标量化处理,以使不同变数处于同样数量级上而便于比较。这就是引入新变数Z,令
(5)
于是局部模型函数变为
(6)
上述βZ表示回归系数β是由Z变数估计,它们在统计学又称为标准化回归系数。βZ的最小平方估计为
(7)
所采用的是Hoerl等建议的计算方法
(8)
式中,D+1为回归模型的参数数目(不包括β0);s2为式(7)的离回归均方;biZ为对于βiZ的最小平方估计数。式(8)实际上是离回归均方对回归系数平方平均值的一个比率。
1.4算法评估
1.4.1算法比较
1.4.2评价标准
采用下述指标进行模型预测效果的检验:
(1)均方误差(root mean squared error, RMSE)
(9)
(2)平均绝对误差(mean absolute error, MAE)
(10)
实验中还将对RDMBL与其他比较算法的平均绝对值进行配对t检验,以验证算法改进效果的统计显著性。
2 结果
设定M=150,即先采取5 s的数据构建初始训练集,在预测阶段随着新数据的采集按照先进先出原则动态更新。选定τ=12(0.4 s)以实现呼吸运动特征与测量噪声之间的平衡;L=30(1 s)已经足够应对延时长的情况;D=2以最小化预测所花费的时间。各种方法的平均绝对误差和均方误差如表2所示。
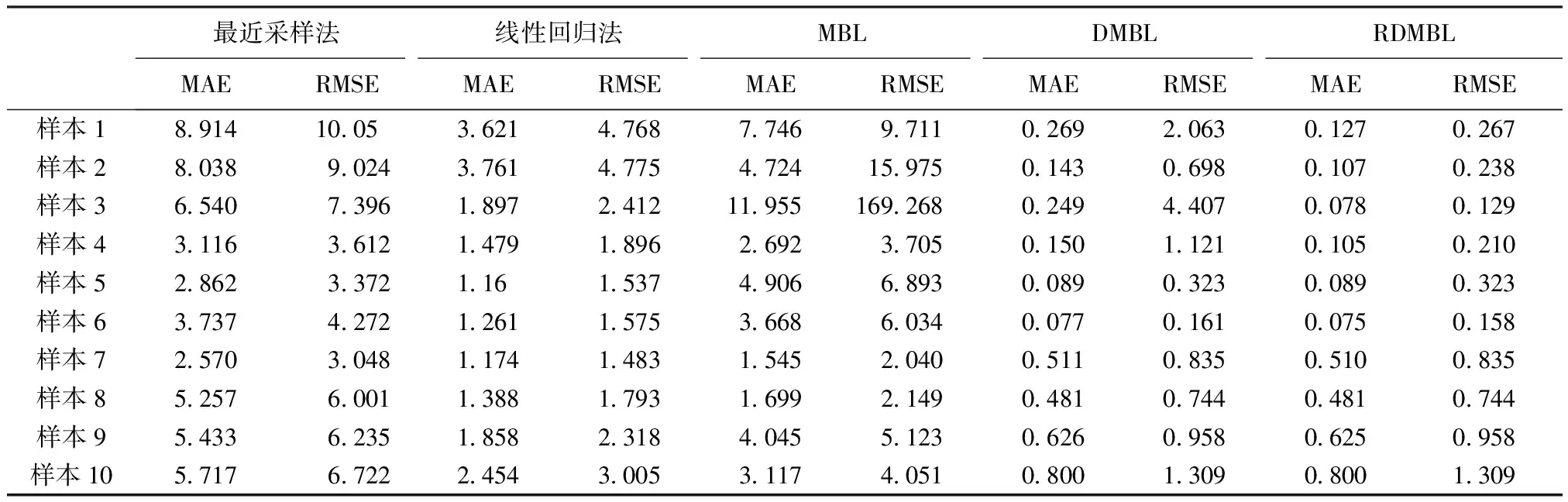
表2 不同方法结果比较(单位:mm)
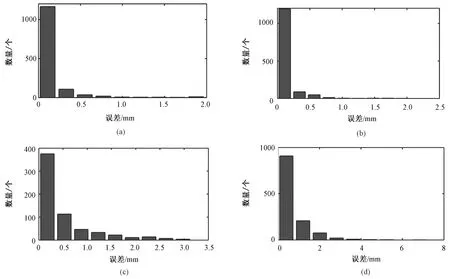
从表2可以清楚比较各种方法的优劣。从总体性能表现来看,最近采样法 从表2和图2结果来看,采用动态更新训练集方法后,DMBL的精确性和抗噪声鲁棒性有了很大的提高,但结合图2(b)可以看出某些时刻仍存在因病态矩阵而出现大的误差。从图2(c)中RDMBL的性能表现可以看出,进一步使用脊回归改进后消减了病态矩阵的影响,使得预测误差降到了最低。实验中,在预测样本1,2,3和4呼吸信号时出现了严重病态矩阵问题,因此使用脊回归后预测性能改进明显;而其他信号没有或出现趋良态的病态矩阵,脊回归的作用就没有体现出来。图3中(a)和(b)表明当DMBL出现严重病态矩阵的情况下,RDMBL能消除大的误差,从而提高性能。图3(c)则表明当病态矩阵问题不明显时,相比DMBL,RDMBL无法进一步改进性能。 为评估实测性能及差异的统计显著性,表3为RDMBL与其他算法的t检验结果,其中RDMBL与最近采样法、线性回归法和MBL比较的P值均小于0.05,这表明相比传统算法,所提出的改进方法对性能提升具有统计显著性。而RDML与DMBL的t检验结果P=0.082,在a=0.1的显著性水平下,说明脊回归在一定程度上提升了算法性能。 图2 不同算法对样本3的预测误差曲线图。(a) MBL;(b) DMBL;(c)RDMBL。Fig.2 The prediction errors on sample 3 using different algorithms. (a) MBL; (b) DMBL; (c) RDMBL. 表3 RDMBL与其他算法的t检验结果 图3 DMBL和RDMBL的预测结果比较。(a)样本1;(b)样本4;(c)样本8。Fig.3 The comparison between DMBL and RDMBL. (a)Sample 1; (b)Sample 4; (c)Sample 8 图4 绝对误差直方图。(a)样本1;(b)样本4;(c)样本8;(d)样本9Fig.4 The histograms of the absolute error.(a)Sample 1; (b)Sample 4; (c)Sample 8; (d)Sample 9 最后,图4是RDMBL预测值与真实值的绝对误差直方图分布,结合图1、图3和表2可以看出当呼吸运动曲线较为规则时,拟合效果好,误差小,当曲线不规则时误差比较大,这是因为当前查询点与训练数据集相似性低,但动态更新训练集法使得算法能迅速适应新数据,在图4中的直方图表现为不管呼吸运动轨迹是否规则,绝大部分时间点的预测值与实际值的误差集中在很小值范围,充分说明了算法具有很好的稳健性和精确性。另外,执行一次RDMBL预测算法仅需要约1 ms,完全适用于实时预测。 基于记忆学习法主要依赖历史数据描述自变量与因变量的关系,它寻找历史状态中相似的“近邻”并利用这些“近邻”预测下一个时刻的状态。呼吸运动有复杂的非线性特征和迟滞现象,构造适当的自变量可以捕捉其运动特性。相比直接由当前观测值构成状态向量,本文采用一种扩展状态向量法,即自变量由当前观测值与最近两个反映迟滞时间的历史样本生成一个扩展的状态,能更准确地把握感兴趣时间点的局部动态特征。采用高斯核距离加权函数判断当前数据与历史数据的相似性,在选择带宽时,采用西尔弗曼法则而不是常用的交叉验证,可以减少运算量。基于记忆学习法对训练数据集要求较高,由表2和图2(a)可以看出,MBL在训练数据过少时难以捕捉呼吸运动的动态特征,预测误差非常大。由图2(b)可知,采用“滑窗法”动态更新训练集后,由于始终包含最新数据,绝大部分时间能够跟踪系统的动态变化特征。从表2看出,DMBL相比MBL,平均绝对误差和均方误差均大幅度下降,说明选择合适的动态更新训练集方法可以有效减小训练集规模并提高估值的准确性。 但从图2(a)和图3可以看出,DMBL在某些时刻仍存在较大的误差,原因是回归分析中信息矩阵通常会因为“过拟合”导致病态,而且病态矩阵问题还未有很好的解决方法。回归分析在放疗中呼吸预测和构建内-外关系都有运用,当样本过小尤其内部肿瘤运动数据样本数量稀疏时,很可能会遇到病态矩阵问题,一般的处理方法是扩大样本,这显然不适用于实际要求。本研究首次尝试在放疗中运用脊回归给病态矩阵引入一个适当小的偏差来提高估计数的稳定性和准确性。由图3和表2中数据的对比结果可以看出,脊回归可以消除因严重病态矩阵引起的大误差,但对趋良态的病态矩阵的作用并不明显。采用有效的方法减小甚至消除病态矩阵带来的消极影响也是回归分析的重要课题,本文的尝试有借鉴意义但不完善,可以跟踪该方向的最新文献寻找脊回归的优化方法或更为有效的新方法。 本研究结合动态更新训练集方法和脊回归算法,提出一种改进的基于记忆学习法,对实验中所使用的十组数据,实现了用高效的方式(每次估值耗时约1 ms)动态跟踪并且预测复杂的呼吸运动,平均绝对误差仅约0.3 mm(0.08~0.8 mm)。并且,用t检验证明了实验结果的统计显著性。实验结果表明,改进后的算法精确性高,实时性好,由于加权函数的局部特性和脊回归的作用,该算法有着很好的稳健性,特别适合处理误差大或被异常值污染的情形。而且,该模型适用于延时较长的系统。 上述模型为实时跟踪放疗中系统延迟问题提供了一种有吸引力的解决方案,下一步的工作应用到大量临床数据进行测试[9],考虑采用多点跟踪,并且建立起外部呼吸标识物运动和肿瘤运动之间的精确关系,从而与肿瘤靶区跟踪技术相结合,那么在胸腹部肿瘤放射治疗中将会有更加实际的临床应用。 [1] Jin JY, Yin FF. Time delay measurement for linac based treatment delivery in synchronized respiratory gating radiotherapy [J]. Medical Physics, 2005,32(5): 1293-1296. [2] Murphy MJ. Tracking moving organs in real time [J]. Semin Radiat Oncol, 2004,14(1): 91-100. [3] Gierga DP, Brewer J, Sharp G,etal. The correlation between internal and external markers for abdominal tumors: Implications for respiratory gating [J]. Radiation Oncology Biol Phys, 2005,61(5): 1551-1558. [4] Krauss A, Nill S, Oelfke U. The comparative performance of four respiratory motion preditors for real-time tumour tracking [J]. Phys Med Biol, 2011,56(16): 5303-5317. [5] Li Ruijiang, Lewis JH, Berbeco RI,etal. Real-time tumor motion estimation using respiratory surrogate via memory-based learning [J]. Phys Med Biol, 2012,57(15): 4771-4786. [6] Ruan D, Fessler JA, Balter JM. Real-time prediction of respiratory motion based on local regression methods [J]. Phys Med Biol, 2007,52(23): 7137-7152. [7] 莫惠栋. 脊回归技术及其应用 [J]. 作物学报, 2002,28(4): 433- 438. [8] 莫惠栋. 回归分析中的病态矩阵及其改进 [J]. 作物学报, 2006,32(1): 1- 6. [9] Ernst F, Dürichen R, Schlaefer A,etal. Evaluating and Comparing Algorithms for Respiratory Motion Prediction [J]. Phys Med Biol, 2013,58(11): 3911-3929. TheStudyonPredictingRespiratoryMotionviaMemory-BasedLearninginRadiotherapy WAN Wei-Quan1ZHANG Hui-Lian2XU Zi-Hai3HE Zhi-Qiang1CHEN Chao-Min1* 1(InstituteofBiomedicalEngineering,SouthernMedicalUniversity,Guangzhou510515,China)2(GuangdongSunwahTechConsultingGroup,Guangzhou510515,China)2(RadiotherapyCenterofPLA303Hospital,Nanning530021,China) Prediction is necessary to compensate the system latency in the real-time tracking radiation therapy for thoracic and abdominal cancers. However, because of the complexity of the breathing motion, conventional methods are far from clinical requirements. This paper proposed a memory-based learning method to predict respiratory motion. The method stores the training data in memory, then finds relevant data to answer a particular query. Furthermore, the paper adopts dynamic update the training data method and ridge regression aimed at “ill-condition matrix” to greatly improve the accuracy and robustness of the algorithm. Our experiment collected ten respiratory motion data with average amplitude of 20 mm (9.2~37.8 mm) from humans’ body surface using POLARIS infrared positioning system. Using our methods (prediction horizon is 1s), mean absolute error (MAE) was reduced to 0.3 mm (0.08~0.8 mm), per estimate takes 1 ms. The results confirm that the proposed method is able to capture highly complex breathing movement accurately in real time. radiotherapy;memory-based learning;respiratory motion;real-time;prediction 10.3969/j.issn.0258-8021. 2014. 02.003 2013-06-20, 录用日期:2014-02-10 广东省重大科技专项 (2012A080104010) R814 A 0258-8021(2014) 02-0148-07 *通信作者。E-mail: gzccm@fimmu.com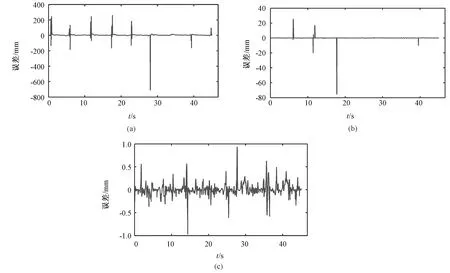


3 讨论和结论

