基于次低价中标法的最优投标报价模型

郭林锋 李秀君 赵雪美

(1.上海理工大学环境与建筑学院，上海 200093； 2.南京理工大学计算机科学与工程学院，江苏 南京 210094)

·招标投标·

基于次低价中标法的最优投标报价模型

郭林锋1李秀君1赵雪美2

(1.上海理工大学环境与建筑学院，上海 200093； 2.南京理工大学计算机科学与工程学院，江苏 南京 210094)

根据评标采用次低价中标原则，建立了使中标概率最大的最优投标报价模型，结合Matlab软件，给出了该模型的求解程序，并罗列出在不同的投标单位数目下，最优投标报价与招标控制价的关系式，结果表明所建立的模型能较大幅度地提高中标率。

投标报价，次低价中标，最优，中标率

随着我国建设项目投资的不断扩大，建设工程招标制度使用的范围越来越广，招标已成为我国建设工程施工发包的主要形式。除法律规定的特殊工程外，绝大多数建设工程都要通过招标选择施工单位。建设工程施工投标对施工企业的经营起着重要的作用，企业是否能够投标成功已经成为企业生存和发展的重要条件。在建筑工程的招投标过程中，确定中标的方法多种多样，主要有经评审的最低价法、次低价中标法、最接近标底中标法和综合评估法等[1，2]。与最后两种评标方法相比，第一种方法透明性强、不易被人操纵，而且能够降低招标成本，但在过度激烈的竞争中，有的单位以较低造价报价，中标后为了能够获利，而降低工程质量，使得运用最低价法评标失去其本质目标。为了改善因评标采用最低价法而带来的弊端，次低价中标法被招标单位所采纳，并且在实际评标过程中运用的越来越多。评标采用次低价中标法，不仅能防止施工单位过度压低报价，而且它也具有透明性强、不易被人操纵、能够降低招标成本等优点。

随着招标单位所选择评标方法的不同，投标报价的策略也随之而改变。近年来最优投标报价问题的研究取得了一系列丰硕的成果，评标采用综合评估法可以利用模糊数学[3]、频率直方图[4]、公式法[5]等方法确立最优报价，评标采用经评审的最低价法可以应用概率分布法[6,7]、博弈理论[8，9]等方法确定最优报价，而评标采用次低价法的数学模型较少。本文则主要运用概率分布法建立评标采用次低价法的最优投标报价模型。

1 模型的假设

1)招标人给出的招标控制价准确合理，能够反映工程实际情况，且能为投标单位投标报价提供正确的引导。

2)所有参加投标的单位都符合招标文件中的资质要求。

3)参加投标的单位相互独立，无信息沟通，更不会出现围标现象。

4)投标单位所雇用的造价人员熟悉工程量清单规范，制作的标书无原则性错误，即不会产生废标。

5)评标遵循公开、公平和公正原则，且采用“次低价中标”的评标原则。

2 模型的准备

2.1 确定投标报价的区间

在招标单位发布的招标文件中，都包含着招标控制价。投标单位进行投标时，其投标报价不得高于招标控制价，一旦高于招标控制价，都作废标处理。由此可以看出，投标报价所在区间的最大值即为招标控制价。

根据工程量清单规范可知：以社会平均成本作为参照的招标最低价B是以招标控制价A下降一定幅度K来计算的[10，11]。计算公式为：B=A×(1-K)，其中K=K1×Q+K2×(1-Q)，K1与K2在建筑工程(含随主体发包的装饰装修、安装、室外总体等工程)中取值区间为6%～12%，Q的取值区间为30%～70%。根据放缩法可知K≤12%，因此B≥0.88A。根据假设4)认为投标人熟悉工程量清单规范中上述基本内容，因此可以认为所有投标报价均在[0.88A,A]区间内。

2.2 确定投标报价的区间

根据假设5)评标采用“次低价中标”的评标原则，可以认为大多数单位投标报价都是偏向区间[0.88A,A]的左侧。将投标报价看作区间[0.88A,A]上的随机变量，其概率密度函数趋于偏左侧的偏态分布。

由于β分布根据参数的不同可以描述不同的偏态分布，而且它可以通过三点估计法确定分布中的参数，是一种常用的、适合描述投标报价的概率分布[12]。因此，本文选择β分布来描述投标报价的概率分布。

β分布由变量的最小值a、最大值b和形状参数r，s确定，其密度函数为：

(a≤x≤b,r>0,s>0)

(1)

(2)

(3)

其中，a为变量的最小值；b为变量的最大值；r，s均为密度函数的形状参数。

2.3 确定密度函数中的参数

β分布的密度函数可以由三点估计来确定，即形状参数r,s可根据变量的最小值a,最大值b和众数m来确定。根据经验公式，三点估计法的β分布均值和方差的估计值分别为[13]：

(4)

(5)

其中,a为变量的最小值；b为变量的最大值；m为众数。

根据上面的式子，只需知道a，b,m的数值，就可以求解参数r和s，而变量的最小值a,最大值b和众数m分别与最小报价值a′,最大报价值b′和最可能报价值m′相对应，其中a′=0.88A，b′=A，关键是确定m′的数值。

2.3.1 确定最可能报价值

2.3.2 分布区间的标准化及参数的确定

由于众数m与投标单位数目n有关。因此，对于不同的投标单位数目而言，随机变量x在区间[0,1]上的概率密度函数是不一样的。但是，只要投标单位数目n是确定的，无论最高控制价A取何值，该概率密度函数都是固定的。如图1,图2所示，在投标单位数目n=3的情况下，图1中的概率密度图形会随着最高控制价A的变化，而发生位置与形状的改变。而图2中的概率密度图形与最高控制价A无关，是一个位置和形状都确定的图形。与图1相比，图2无需考虑最高控制价A，更加简洁明了。因此，对分布区间进行标准化，能够将具有相同投标单位数目的概率密度函数统一化，更有利于求解最优投标报价问题。

(6)

其中，n为投标单位的数目。

从形状参数r和s表达式也可以看出：随机变量x在[0，1]区间上的概率密度函数仅与投标单位数目n有关；对于不同的投标单位数目，该概率密度函数是不一样的。

在投标的过程中，可以根据投标单位数目n以及式(6)，得出形状参数r和s的数值，进而确定出在[0，1]区间上的概率密度函数。

3 模型的建立与求解

3.1 模型的建立

根据次低价中标原则，当有n家单位参与投标且投标报价c′A为中标价时，说明没有中标的n-1家单位中有一家单位投标报价在区间[0.88A,c′A)内，其他n-2家单位的投标报价在区间(c′A,A]内。因此，以c′A作为投标报价，其中标概率为：

(7)

其中，n为投标单位的数目；A为最高控制价；c′为报价系数；f(t)为投标报价的概率密度函数。

(8)

(9)

为了使该中标概率最大，可以建立以下模型：

(10)

根据上面对式(7)的简化，可以将该模型简化为：

(11)

3.2 模型的求解

4 模型的结果分析与评价

1)在建设工程招投标中，只要是根据次低价中标原则来评标，就可以运用该模型来确定最优投标报价。通过该模型，只需知道招标最高控制价A和参加投标单位的数目n，就可以定出最优投标报价，使得该投标报价的中标概率最大，而在实际招投标过程中最高控制价和参加投标单位数目都是可知的，由此，可以看出该模型实用性较强。

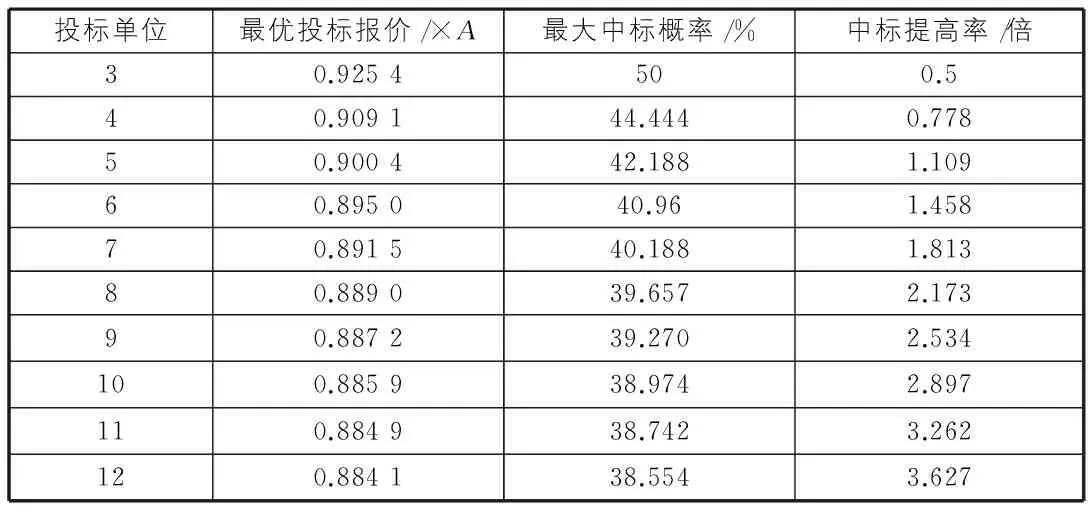
表1 模型求解数据表

2)根据最大中标概率与投标单位数目n的关系图(见图3)，可以看出：随着投标单位数目n的逐渐增加，运用该模型得到的最大中标概率逐渐趋近于某一定值。

3)运用该模型得到的中标概率与平均中标概率相比，其中标提高率的表达式如下所示：

(12)

从中标提高率与投标单位数目n的关系图(见图4)，可以看出：中标提高率趋于线性增加，并且增加的幅度较大。结合表1，还可以看出：当投标单位n=5时，运用该模型得到的中标概率已经比平均中标概率提高了1.109倍，而且随着n的增加，中标提高率增加的倍数越大。由此可知：投标单位越多，运用该模型对提高中标率越有利。

4)本文还给出了在Matlab中求解最优投标报价的程序，投标人可以运用该程序，根据提示，输入参加投标单位的数目n和最高控制价A，就可以得到最优投标报价。如果参加投标单位的数目n在表1范围内，还可以根据表1直接确定最优投标报价，使中标概率最大。在实际的投标过程中，投标单位可以根据本模型所得的最优投标报价作为报价的参考依据。

5 结语

在建设工程招投标中，次低价中标原则凭借自身的优势，在评标中应用越来越广泛，而此种原则下的投标报价模型较少。本文提出一种最优投标报价模型，只要是根据次低价中标原则来评标，就可以运用该模型来确定最优投标报价。投标单位只需根据招标控制价和参与投标单位的数目，运用本文提供的Matlab程序或者表1中的关系式，就可以确定使投标单位中标可能性最大的投标报价。运用该模型得到的最优投标报价进行投标，其中标概率比仅有3家单位参加投标的平均中标概率还要大，并且能够较大幅度地提高中标概率，使得企业更具有竞争力。因此，在实际的投标过程中，为了能够使企业中标的概率最大，投标单位可以参照本文提出的模型进行投标报价。

附程序1：本文所建立最优投标报价模型的计算机程序(MATLAB[14])。

clc;clear;

n=input(’请输入n的值:’)

symsx

a=0;b=1;

r=(n+4)*(2*n^2+8*n-8)/(3*n^3)

s=(5*n-4)*(2*n^2+8*n-8)/(3*n^3)

j=betainv(1/(n-1),r,s)

c=(1-0.88)*j+0.88

c=vpa(c,10) %改变c的精度,可使最优投标报价精确至分

A=input(’请输入招标控制价A的值’)

B=A*c;

fprintf(’最优投标报价:’),B

[1] 林奕文.浅谈工程投标中最低价中标的利弊[J].广东土木与建筑,2002(8):41-42.

[2] 贾长麟.对最低价中标评标方法的信息经济学分析[J].建筑经济,2008(5):76-78.

[3] 邓铁军,欧 莉,龚亮英.工程投标报价策略模型的研究及其运用[J].株洲工学院学报,2004,18(5):57-60.

[4] 孙洪涛.建筑工程投标报价数学模型探讨[J].甘肃科技纵横,2006,35(5):161-162.

[5] 张 曙.复合法评标方式下最优投标报价研究[J].铁路工程造价管理,2009,24(2):16-18.

[6] Lawrence Friedman. A Competitive-Bidding Strategy[J]. Operations Research,1956,4(1):104-112.

[7] 贾长麟.最低价中标规则下企业最优投标报价研究[J].武汉理工大学学报,2010,32(3):490-493.

[8] John G Riley, William F Samuelson. Optimal Auction[J].The American Economist,1981(71):381-392.

[9] 蓝筱晟.最低价中标法的投标博弈研究[J].价值工程,2011(15):75-76.

[10] 杨琳琳.房地产项目最低价中标法的投标报价合理性研究[J].绵阳师范学院学报,2012,31(7):20-22.

[11] 陈 群,孙 磊.蒙特卡罗法在投标报价中的应用[J].武汉理工大学学报,2009,31(3):503-506.

[12] 姜鹏飞.设计投标中的蒙特卡洛模拟报价研究[J].工业技术经济,2009,28(8):104-106.

[13] 王卓甫.工程项目风险管理——理论、方法与应用[M].北京:中国水力水电出版社,2002:96-97.

[14] 蒲 俊,吉家锋,伊良忠.matlab6.0数学手册[M].上海:浦东电子出版社,2009:144.

Optimal bidding price model under the rule of secondary low bid

GUO Lin-feng1LI Xiu-jun1ZHAO Xue-mei2

(1.SchoolofEnvironmentandArchitecture,ShanghaiUniversityofScienceandTechnology,Shanghai200093,China；2.SchoolofComputerScienceandEngineering,NanjingUniversityofScienceandTechnology,Nanjing210094,China)

According to the rule of secondary low bid, an optimal bidding price model was established in the above conditions which could maximize the winning rate of the bid. Moreover, this paper also presented a Matlab program to solve the model and the relationship between optimal bidding price and bidding control price with different bidder numbers. Result analysis of the model showed that the established optimal bidding price model can greatly improve the winning rate of the bid.

bid price, secondary low bid, optimal, winning rate of the bid

1009-6825(2014)34-0241-04

2014-09-22

郭林锋(1988- )，男，在读硕士； 李秀君(1976- )，女，博士，副教授； 赵雪美(1988- )，女，在读硕士

TU723.2

A